高反光陶瓷基片缺陷检测

柴进平，罗敏，孙国浩，谢石磊

（1.湖北汽车工业学院，湖北 十堰 442002；2.河南诺米智能科技有限公司，河南 郑州 450000）

在贴片电阻的生产过程中，底片—陶瓷基片的质量检测极为重要，质量过关与否直接影响后面工序能否正常进行以及最终产品的精度。目前陶瓷基片表面质量的检测工作主要通过人工目检完成，不仅效率低下，而且容易受到主观意识和人体疲劳等因素的影响。利用机器视觉进行检测能解决这些问题。在机器视觉系统采集时，由于受陶瓷基片表面光滑等因素的影响，常常出现光照不均匀现象，增加检测难度。针对此现象，提出的校正方法有同态滤波方法、直方图均衡化方法、基于模糊理论的方法、Retinex方法、伽马校正方法等。同态滤波方法可以使图像过暗区域的光照得到增强，同时又可以保护图像的细节［1-2］，但因为是直接分离出属于高频部分的反射信息进行相应处理，无法对输入图像中属于低频部分的高亮区域进行校正。直方图均衡化方法具有简单、快速的优点，但主要作用是将集中在某个较小灰度区间的直方图转换为在整个灰度区间均匀分布的直方图［3］，对光照不均匀这种高对比度图像的整体校正效果并不理想。基于模糊理论的校正方法能判定出高亮度和低亮度区域并分别处理，但参数选取困难且计算复杂［4］。Retinex方法具有色彩恒常性，但在亮度突变区域会出现光晕现象［5］，有学者结合具体应用场景提出了改进措施［6-7］，处理效果显著，但算法复杂，速度较慢。伽马校正方法能提升图像的对比度，但存在欠饱和或者过饱和的问题，改进伽马校正方法虽然解决了上述问题，但算法所需时间较长［8］。文中在频域中进行光照分量提取，提高处理速度；针对灰度细节较少的特点，采用伽马变换（全局伽马修正系数）增强提取到的光照分量，使光照不均匀的校正效果更明显；对校正后的图像再进行缺陷检测。

1 检测对象及算法

贴片电阻因耐潮湿、耐高温、体积小、可靠性高、外观尺寸均匀、精确以及温度系数与阻值公差小等优点，被广泛使用［9］。陶瓷基片是生产贴片电阻的基础材料，易出现气泡、无刻痕、缺损、裂纹等缺陷，裂纹缺陷的影响最严重。针对0402 贴片电阻陶瓷基片的质量检测，提出机器视觉检测算法。

检测的陶瓷基片尺寸为50 mm×50 mm×0.5 mm，检测精度为0.1 mm。为避免电机工作给采集图像带来干扰，选择500万像素的面阵相机。经过实际效果的比较，考虑现场架设，采用照明角度为60°的环形光源，接光源控制器。采集系统架设见图1。

图1 图像采集系统图

采集的陶瓷基片图像见图2。光照强度较低时，裂痕缺陷不明显，即使后续进行图像增强，但由于原始图像中缺陷的对比度较低，实际检测效果不理想，准确度较低，平均为86.7%左右。随着光照强度的增强，虽采用了环形光源提供光照，但陶瓷基片是高反光材料，且每次放置的位置略有波动，所以依然会出现光照不均匀现象。从图2可看出：要检测的缺陷形状为线型，且与周围的像素值具有一定的对比度，故先通过带通滤波器进行滤波处理，然后通过自适应全局阈值分割及形态学处理将缺陷区域找出，利用高斯线性函数进行亚像素精度的XLD（extended line descriptions）轮廓提取。

图2 不同光照强度下采集的陶瓷基片图像

带通滤波器是通过指定频率段的信息，拦截其他频率段的信息，示意图如图3所示。创建合适的频域带通滤波器，利用傅里叶变换将输入图像转换至频域并进行滤波，得到指定频率段信息。将滤波后的图像转换回空间域进行自适应全局阈值分割、形态学处理，疑似缺陷区域便都被分割出来。设置适当的参数，利用高斯线性检测算法便可准确地将裂痕缺陷提取出来。图像采集过程中，往往会出现光照不均的现象，使得缺陷信息被遮盖或者误把明暗相接处当作裂痕缺陷，导致漏判或者错判。因此，在进行缺陷检测前先进行图像校正。Retinex理论指出：在某个指定的波段内，反射能力是物体的固有属性，如果能提取到光照分量和反射分量，在颜色恒定的约束下，便可去除光照分量对输入图像的影响，只留下物体本身的反射特性［10］，达到校正图像的目的。检测算法流程见图4。

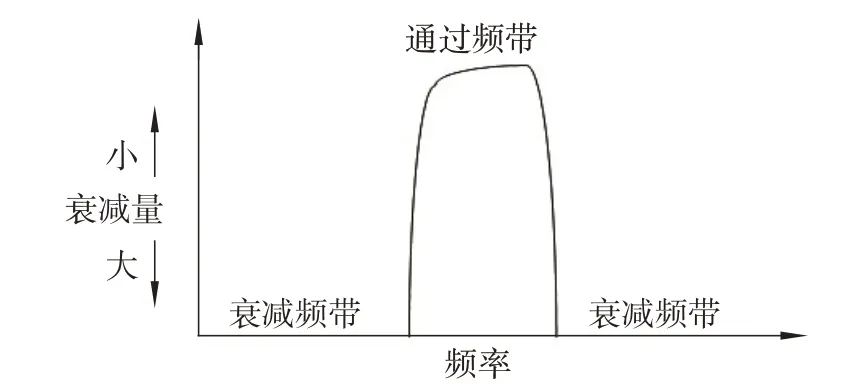
图3 带通滤波器

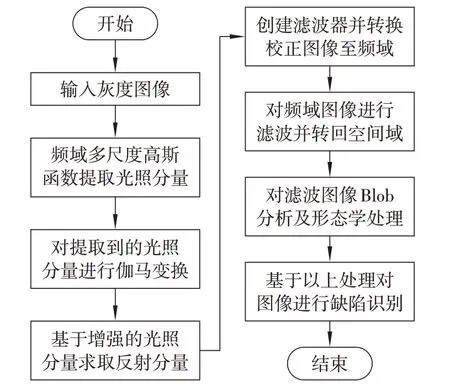
图4 检测算法流程图

2 图像增强算法

2.1 频域提取光照分量

依据Retinex 理论，设输入图像为I（x,y），光照分量为L（x,y），反射分量为R（x,y），则有如下关系：

式中：Lg（x,y）为光照分量的估计值；*为卷积运算符；G（x,y）为低通滤波的高斯函数；（μx,μy）为高斯滤波掩膜中心点的坐标；σ为高斯分布函数的标准差。式（2）是单尺度高斯函数提取出光照分量。

为了增强提取效果，采用多尺度高斯函数进行提取。多尺度高斯函数提取光照分量即多个单尺度高斯函数提取结果进行加权求和：

式中：wi为第i个高斯函数的权重；n取1，即单尺度；n大于1表示多尺度。如n取3时，权重w1～w3均取1/3，σ1取3，σ2取4，σ3取5。

式（3）是在空间域对输入图像进行光照分量提取，会嵌套多层循环结构，导致运算量较大、运行时间较长。卷积定理表明，空间域中的卷积相当于频域中的乘积［1］，所以在频域中进行光照分量的提取，可一定程度上加快运算速度。实际计算时，先对式（3）两边进行傅里叶变换，将空间域中的卷积运算转换为频域中的乘积运算，得到频域中的光照分量估计值F（Lg）：

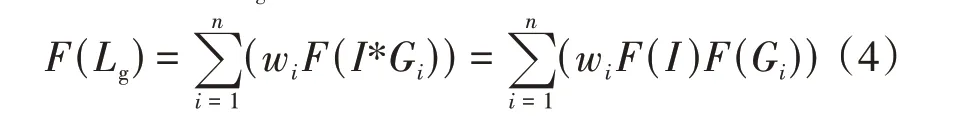
再对F（Lg）进行傅里叶逆变换，得到空间域光照分量Lg（x,y）。

2.2 求取反射信息图像

依据Retinex 模型，求出反射分量以去除光照分量的影响。为了使反射分量更加清晰，裂痕缺陷更加明显，先对光照分量进行非线性全局γ变换：

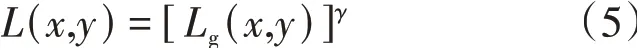
式中：γ为全局修正参数，取值范围为0.1～10。γ小于1时，变换后的图像更亮；值越小，变换后的图像越亮。γ＞1时，变换后的图像变得更暗；值越大，变换后的图像越暗。不同的值，对应的变换关系也不同，根据陶瓷基片的实际修正效果，文中γ取0.76。

得到修正后的L（x,y）后，依据式（1）对R（x,y）进行求取，得到清晰的反射信息图像。为了运算方便，对式（1）进行变换：

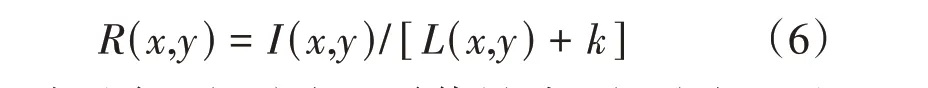
式中：k为避免L（x,y）出现零值导致R（x,y）出现过饱和现象而引入的常数，根据实际效果取值，一般取光照分量均值的1%。

2.3 效果图

校正前后的图像效果如图5 所示，可以发现：校正后的陶瓷基片图像光照明显变得均匀，且缺陷的对比度较好地保留了下来。

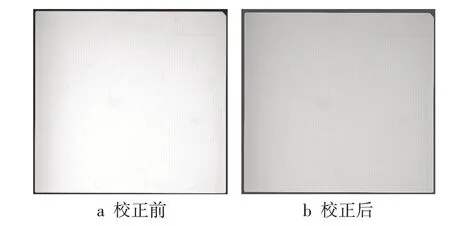
图5 校正前后的陶瓷基片图像

3 缺陷定位与分割

根据缺陷与工件本身的对比度设计合适的频域带通滤波器，生成正弦形状的带通滤波器B，如图6b 所示。对待处理图像R（x,y）进行取反，如图6c所示。将取反后图像Rf（x,y）转换至频域。

图6 缺陷检测过程图

针对定位到的区域，利用高斯线性函数进行亚像素精度的XLD 轮廓提取，若存在缺陷，用红色线圈出，效果如图6d所示。

4 实验结果与分析

通过对比米粒图像和陶瓷基片图像的不同方法处理效果来验证文中方法的有效性，见图7～8。用3 个重要指标来衡量算法对原始图像的增强性能及有效性，分别是图像平均灰度、图像熵以及算法运行时间。图像平均灰度反映的是图像的亮度信息，通过比较原始图像与处理效果图的平均灰度，可判断图像亮度是否得到了提升。对于光照不均匀的图像，校正后的图像是否变得更亮是判断校正算法是否有效的重要标准之一，即校正后图像的平均灰度越高，图像的校正效果越好［11］。图像熵反映的是图像的灰度分布，图像熵的值越小，表示图像的灰度分布越均匀，也表明校正的效果越好；相反，图像熵的值越大，则表明校正效果越差。算法运行时间是衡量算法优劣的重要指标，尤其在工业项目的应用中，检测速度是最受重视的参数之一。

图7 米粒图像与不同方法处理结果的比较

图8 陶瓷基片图像与不同方法处理结果的比较

表1～2列出了2组图像3项指标的值。1）在校正效果方面，文中方法的校正效果更为理想。由表1 可看出：直方图均衡化处理的图像熵是较高的，在米粒图像的处理中甚至比原始图像的图像熵还要高出32 左右，所以直方图均衡化方法的校正效果较差；改进伽马校正处理的图像平均灰度和图像熵较文中方法分别相差18.192、39.527 和4.1838、2.2056，与校正效果图的直观效果相符，此外，改进伽马校正处理的图像平均灰度小及图像熵大，校正后的图像在进行缺陷检测时用时较长，且检测准确度较文中方法低5.3%左右，所以文中方法的处理效果较好。2）算法运行时间由多到少依次为直方图均衡化方法、文中方法、改进伽马校正方法。改进伽马校正方法的用时较文中方法多耗时140 ms左右，这是单独对算法运行时间进行的统计。运用到实际系统中时，每个相机都拥有一个处理线程，加上运行时间、检测数据的实时显示等线程，多线程并行时，相互有一定的竞争，再加上运行环境等因素影响，改进伽马校正方法耗时525 ms左右，文中方法耗时315 ms 左右。根据检测要求，只有在400 ms内完成才能保证检测效率达标，所以采用改进伽马校正方法无法达到检测效率要求。

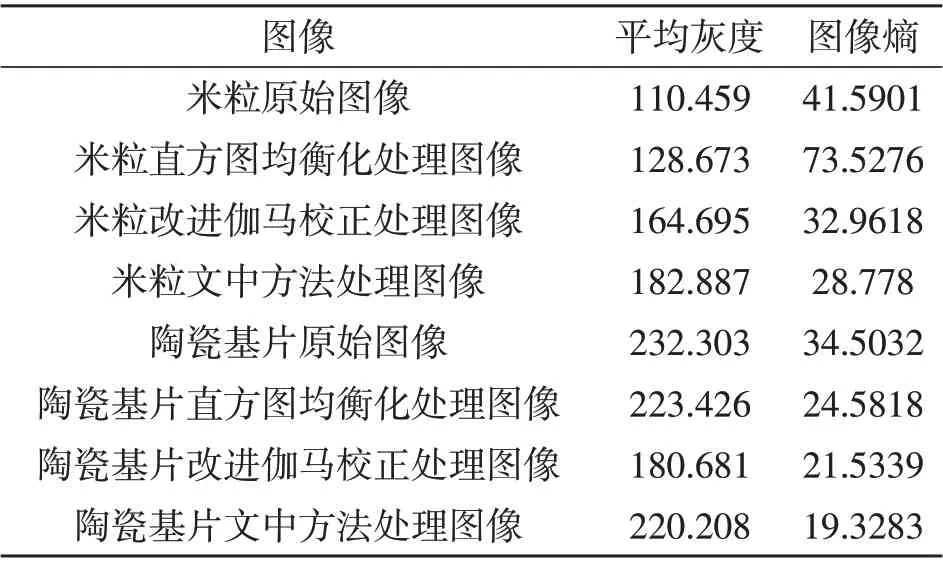
表1 图像平均灰度与图像熵评价指标

表2 不同方法所用时间

5 结论

针对高反光陶瓷基片缺陷检测，文中基于颜色恒常性理论的亮度感知Retinex 模型，利用多尺度高斯函数在频域对输入图像的光照分量进行提取并利用全局伽马修正系数进行增强，基于增强后的光照分量将反射分量从输入图像中提取出来，实现了对输入图像的校正。最后利用频域带通滤波器、形态学处理、高斯线性检测等方法对缺陷进行了检测。通过实际测试，文中方法的检测准确度约为98.6%，检测速度较直接在空间域进行校正和检测提高了20%，具有较高的可行性。