无人驾驶车辆自适应巡航控制策略

白嘉绮，韩同群

（湖北汽车工业学院 汽车工程学院，湖北 十堰 442002）

近年来，汽车保有量增加造成的交通拥堵加剧了驾驶员疲劳，使事故发生率升高［1］。研发具备成熟自适应巡航（adaptive cruise control,ACC）技术的无人驾驶车辆可有效解决此问题。ACC 系统能根据车辆行驶中外界环境的实时变化，自行调整与前车距离和当前车速［2-3］来保证行驶安全。ACC系统工作本质是对车辆底盘进行纵向控制，不同控制算法对车辆的控制效果不同［4］。PID控制结构简单易调节，广泛用于早期ACC 系统研发。Wu Xingchen等人［5］提出改进的可调PID 控制器，降低了两车最小安全距离且提升了车辆乘坐舒适性。K.Yi 等人［6］将前馈控制思想应用到PI控制器中，提升了响应速度。无人驾驶车辆要求控制更精确，尤其是车辆系统的非线性特征增加了控制难度，PID控制无法匹配更高需求的ACC系统。文献［7-8］中将PID控制与模糊控制结合，提高了系统的鲁棒性，但模糊规则缺乏定量评价方法。文献［9-10］采用深度学习算法设计了模仿传统车辆驾驶员驾驶风格的ACC 系统，但算法的实现依托大量数据分析，实时性差。为此，选用分层控制分解ACC 系统控制目标，选择有良好滚动时域优化特性的模型预测（model predictive control,MPC）控制策略。MPC 策略可选用的模型形式多样，与无人驾驶汽车非线性强、需应对复杂多变的行驶环境的特点相吻合。在下层控制器中基于ACC系统工作本质增设轮胎模型，提高系统精度。最后在不同工况下对ACC 控制系统进行仿真，验证其设计合理性与安全性。

1 ACC系统总体架构

无人驾驶车辆ACC系统从结构上分为环境感知层、决策层、控制层3 个层面。环境感知层替代传统车辆中驾驶员眼睛，利用毫米波雷达、加速度传感器、轮速传感器等一系列传感器收集车辆状态信息，并传递给决策层。决策层代替传统车辆驾驶员大脑，根据车载计算机的安全车间距模块和上层控制器模块计算出期望安全车间距与对应的主车期望加速度。控制层取代驾驶员手脚，根据接收到的主车期望加速度信息在下层控制器中转换为相对应的节气门开度或制动压力等，操纵汽车按规划路径前进［11］，如图1所示。

图1 ACC系统结构图

2 上层控制器设计

上层控制器接收环境感知层传递的两车运动状态信息，并进行分析决策。选择合适的上层控制器控制策略是保证ACC 系统性能的基本前提。MPC控制策略能平衡因传感器工作环境造成的外界干扰等原因引发的控制系统扰动，而ACC 系统优化过程需综合协调各项相互矛盾的工作性能，故采用MPC控制能将这些综合控制目标采用加权形式进行处理。

2.1 期望安全车间距模型

跟车模式下，巡航车辆与前方车辆间的安全车间距是ACC系统决策层上层控制器的重要输入和ACC 系统设计的首要参考。车间距过大，道路利用率低；车间距过小，若前方行驶环境突变易发生危险且急速刹车影响乘坐舒适性。因此运用可变安全车间距算法来根据实际情况随时调整安全车间距离［12］，根据车间时距（time headway, THW）可划分为固定车间时距算法（constant time headway,CTH）和可变车间时距算法（variable time headway,VTH）。尽管VTH 算法应对一些复杂路况时控制表现更好，但因其计算过程较为复杂，不利于普及和日常应用，故拟采用稳定性强的CTH 算法作为安全车间距模型设计的基础［13］。基于CTH算法所设计的期望安全车间距模型表达式为

式中：ddes为两车期望安全车间距；ς为跟车时距；vh为ACC 系统自身车辆行驶速度；dmin为两车静止时最小安全车间距；d为两车实际行驶中纵向距离。在无人驾驶车辆安全合理决策范围内ς为1～3 s，dmin为2～7 m［14］，故依据决策区间和所设计的ACC系统应用场景，将THW设为2 s，dmin值设为5 m。

2.2 前后车之间纵向运动学建模

ACC 系统实质是对主车进行纵向控制，因此忽略车辆其他方向运动，仅搭建两车间纵向运动学模型，如图2所示，纵向运动学关系为

图2 前后两车之间纵向运动学关系

式中：Δd为期望安全车间距与实际车间距的误差；v1为ACC 系统自身车辆行驶速度；v2为前方车辆车速；vrel为两车间相对速度。

由于车辆具有非线性特性和运动惯性，ACC系统上层控制器输出的期望加速度信号传递给下层控制算法时存在时间延迟，因此采用1阶惯性环节来解决此问题［15］：式中：a1为巡航加速度；Kl为1 阶惯性系统增益，取1；Tj为1阶惯性环节时间常数，取0.53；S为复频率。

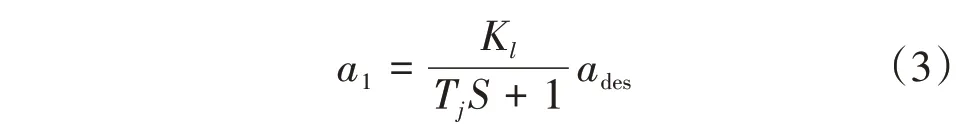
将式（1）代入式（2），得到Δd的表达式，并对其与式（3）中a1同求1阶导数：

基于此，建立上层控制器状态空间方程，定义状态变量x（k）为

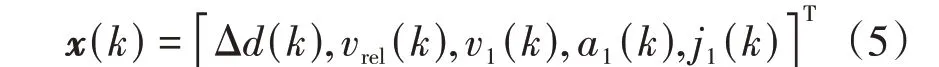
与传统ACC 系统状态变量参数相比［16］，状态变量兼顾了主车加速度变化率j1(k)与v1，并将传统MPC 控制器中状态量d替换为Δd，可直观体现MPC 控制效果，提高控制精度。现阶段环境感知层无法准确获取前车加速度，但对ACC 系统控制有重要影响，则将前车加速度作为系统扰动：

定义ades作为模型预测控制状态方程的控制量u（k）。

综上，采用前项欧拉法将状态空间方程离散化的上层控制器模型表达为

式中：A、B、C为状态空间方程系数矩阵。由此搭建的考虑干扰的离散状态空间方程，更准确，贴近实际，适用于ACC系统上层控制器设计。

2.3 兼顾多目标因素的MPC控制器设计

MPC 控制器需要同时满足行驶安全性、跟车性、舒适性与经济性的控制约束才能保证对ACC系统良好的控制效果。ACC 系统控制最终目标是使d达到期望车间距的同时，巡航车辆车速变化能与前方目标车辆车速变化保持一致，即

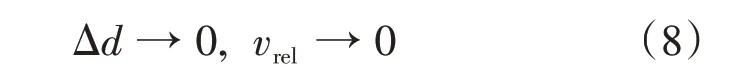
在未达到最终控制目标的跟车过程中有可能实际Δd先为零，出现交通事故，故将提升安全性作为首要控制目标，施加硬约束：

主车跟车行驶中尽可能使a1及j1（k）的变化平缓，提高无人驾驶车辆乘坐舒适性，降低燃油消耗。为此对a1及j1（k）进行硬约束：

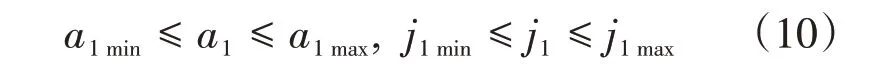
综上，状态变量x（k）中除v1（k）外，其他状态量均作为MPC 控制器的性能指标构成输出向量，得到系统输出方程：

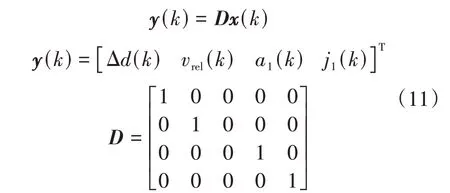
将综合满足所设计的ACC系统上述硬约束的性能指标的最优控制参考轨迹设为

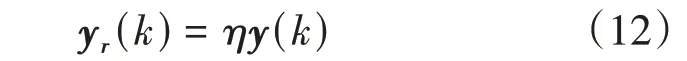
式中：η为各项性能指标对应的权重系数。依据模型预测控制算法，对式（7）～（12）进行迭代后得到标准离散化状态空间方程：

综上，基于式（15）可求解当前时刻ACC 系统巡航车辆的期望加速度。

2.4 上层控制器搭建

在CarSim 中选择某B级轿车作为ACC 系统巡航车辆，将前车车型选择为某D级轿车。进行工况设置时，忽略巡航车辆的节气门开度模块与制动模块，设置自动换挡模式。在道路环境设置中将车辆行驶道路环境设置为水平直线道路，将传感器模块中的传感器检测距离设置为100 m。

因采用CarSim与Simulink联合仿真平台，故在CarSim 中进行整车模型、道路环境及传感器设置的基础上，设置联合仿真接口。CarSim 输出参数分别为前后两车相对距离、相对速度、主车车速、主车加速度、对应发动机转速及4 个车轮的滑移率。Simulink 传递给无人驾驶车辆执行层的参数为节气门开度与制动压力。将设计的MPC控制策略转化为Simulink程序语言，则上层控制器在仿真软件中搭建完毕。

3 下层控制器设计

ACC 系统中下层控制器与上层控制器相互制约，相辅相成。上层控制器用计算出的巡航车辆期望加速度来限制下层控制中节气门开度和制动压力的大小，节气门开度和制动压力的大小又控制ACC 车辆的实际加速度。因此下位控制器要满足抗干扰性强、响应快的设计目标。车辆逆纵向动力学模型是设计好下层控制器，使其达到设计目标的关键，包括发动机逆模型和制动器逆模型。若逆动力学模型相对复杂，则提高了下层控制器准确性，但降低了控制器响应速度，反之亦然。据此，在进行下层控制器设计时要在保证逆动力学模型精确度的前提下尽可能简化。下层控制器作用于ACC系统的流程见图3。轮胎模型在ACC 系统进行底盘控制时有重要作用，选用结构简单且拟合精度高的魔术轮胎模型可改进传统逆纵向动力学模型精度。下层控制器依据上层控制器输出的加速度信息判断当前行驶状态，从而选择传动或制动模型。

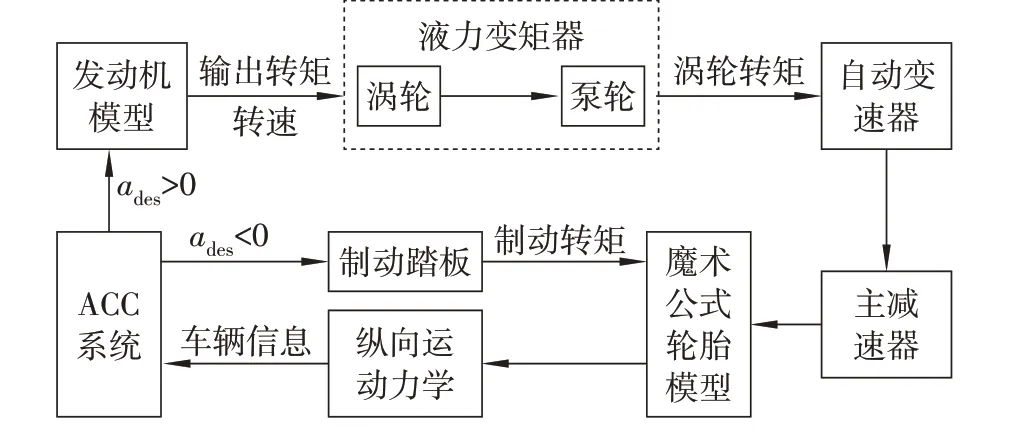
图3 下层控制器中传动系统的总体结构框图

3.1 发动机逆模型

车辆行驶方程式为

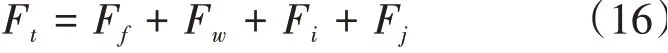
式中：Ft为车辆行驶时发动机产生驱动力；Ff滚动阻力；Fw为空气阻力；Fi为坡度阻力，因所设计的ACC系统暂时不考虑坡面道路，故取0 N；Fj为加速阻力。从车辆自身传动角度考虑，Ft是忽略传动系统的弹性变形，将发动机输出扭矩经传动系统传递到驱动轮上。传动系统部件中机械传递效率、液力变矩器扭矩特性等各项参数作为传动损耗，将这些参数用Ke代替，得到发动机期望输出扭矩Te：

忽略节气门滞后时间及驱动轴扭转刚度对发动机性能影响。据Carsim 中巡航车辆的扭矩特性曲线，利用反查表法得到逆发动机模型。结合Carsim输出到Simulink中的实时转速与通过式（14）计算得出的发动机期望输出转矩，获得与决策层对应的期望节气门开度。结合巡航车辆的实际参数，在Simulink中搭建节气门开度框图模型，如图4所示。

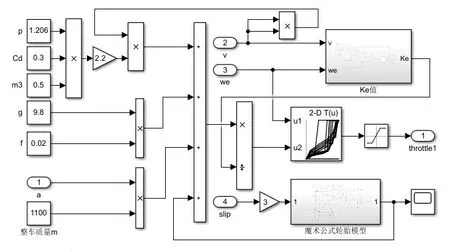
图4 Simulink中节气门开度结构框图

3.2 制动控制器逆模型

当控制层接收到的期望加速度为负值时，表示该无人驾驶车辆决策层需控制制动踏板使车辆减速行驶。此时Ft为0 N，取而代之的是无人驾驶车辆的制动系统将制动转矩传递转化为作用在车轮上的制动压力。制动压力可根据汽车行驶方程式与牛顿第二定律计算得出。为保证车辆制动时安全性，将制动压力与期望制动力设置成线性关系，防止出现车轮制动力过大、超出安全范围出现抱死的现象。在Simulink中建立的制动系统见图5。

图5 Simulink中制动力结构框图

通过对上层控制器中MPC算法的设计及下层控制器中传动系与制动系的分析，基于CarSim/Simulink联合仿真平台的仿真验证模型搭建完毕。

4 仿真结果分析

4.1 前车平稳起停工况安全距离保持模式

车流量较多的城市道路工况中，交通信号较多，车辆行驶速度较慢，故将前方车辆设置为从起步开始到达一定车速后保持定速前进，路遇红色交通信号灯时再逐渐降低车速至0 m·s-1。。此时无人驾驶巡航车辆仅需在保持两车安全车间距情况下跟随前车行驶。设置前车初始车速为0 m·s-1，在第5 s车速达到11 m·s-1时保持恒定，后在第20 s时开始减速，到第25 s 时车速为0 m·s-1。巡航车辆初始车速也为0 m·s-1，两车初始车间距为30 m。仿真结果如图6 所示，可以看出，当前方目标车辆的车速变化时，巡航车辆能快速响应，稳定跟随前车，且在控制过程中使两车间速度误差保持在较小范围内。在ACC 系统控制后车速度过程中，实际车间距与期望车间距误差逐步缩小，在第4 s 之后始终将车间距误差保持在0～5 m，保证行车安全性同时提高了跟车效率与道路利用率。整个控制过程中主车加速度曲线平缓、波动幅度较小，说明基于模型预测控制的分层控制方式拥有较好的经济性与舒适性，控制方式给定的约束条件合理。

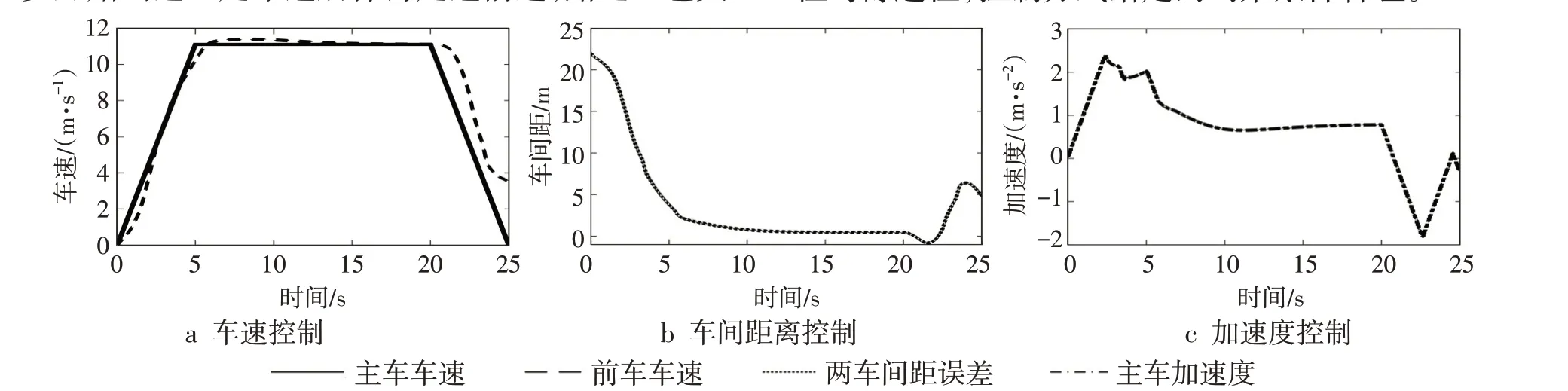
图6 前车起停工况下控制效果图

4.2 前车平稳加减速工况稳定跟随模式

在周围车辆相对较少的郊区等道路条件下，行驶车辆可依据道路环境进行平稳加减速。前后车初始车速设为30 m·s-1，两车初始车间距为30 m，前车以0.225 m·s-2的加速度稳定加速20 s 后保持该车速10 s，再以-0.225 m·s-2的加速度稳定减速20 s，恢复初始车速30 m·s-1。仿真结果见图7，可以看出，初始时刻实际车间距小于期望安全车距，误差为-40 m，两车相对车速加大。第3 s后两车实际与期望距离误差达到安全性要求，此后在保持安全车间距的同时稳定跟随目标车辆，相对车速误差始终保持在较小范围内，最终达到期望值。整个控制过程中加速度曲线始终保持平滑，变化范围不超过2.1 m·s-2，提升了乘客舒适性。

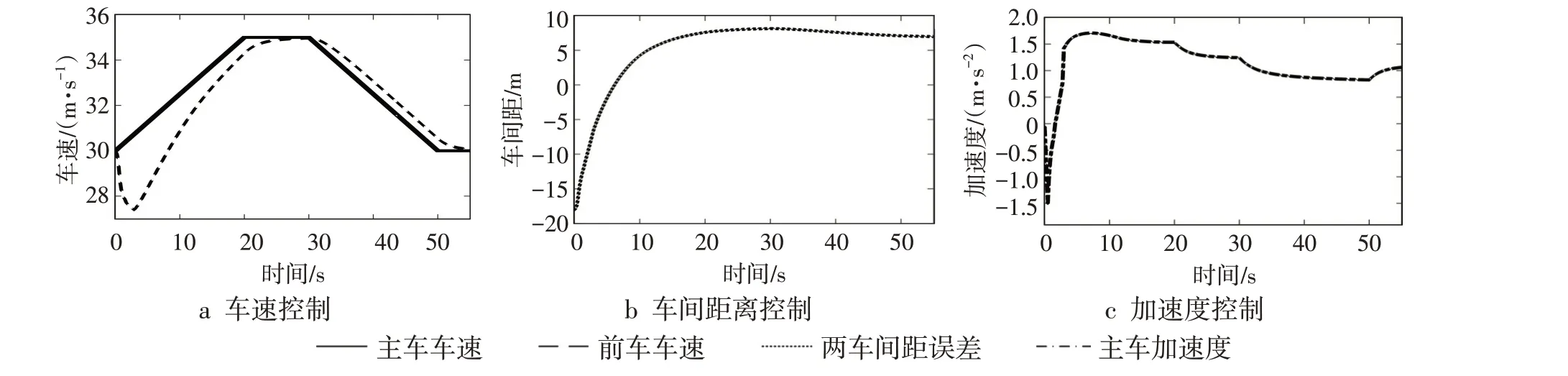
图7 前车平稳变速工况下控制效果图

4.3 前车急加减速工况跟车防碰撞模式

在周围行驶车辆或行人较多的道路环境行驶时，前方车辆可能突然急刹车。为验证此情况下ACC 系统的工作效果，设置后车初始时刻速度均为30 m·s-1，两车初始时刻距离为30 m，前车初始时刻以-8.3 m·s-2的加速度急减速2 s 后保持该车速到第10 s，又以5.8 m·s-2的加速度加速2 s 直至车速到达20 m·s-1，保持该车速行驶。仿真结果如图8所示。

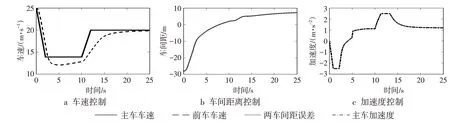
图8 前车急变速工况下控制效果图

将整个控制过程中主车的车速变化整体趋势与前车相对照，发现巡航车辆能较快响应，快速平稳跟随前车。0～2 s 内前车急减速，此时巡航车辆降低车速，避免两车碰撞，证明了基于MPC设计的ACC 控制系统对紧急降速工况有良好的适应性。如图8b所示，整个车间距离控制过程中，初始时刻两车间的实际车间距与理想跟车距离差距较大，但因为要将保证安全性作为首要控制目标，先跟随前车降低车速，后在没有与前车的碰撞风险后快速响应调整，将车间距误差控制在0～5 m，验证了ACC控制系统具有良好的跟车安全性。如图8c所示，第6 s的加速度曲线由于换挡出现峰值跳动，后又快速平稳，未超出设定范围，对车辆的乘坐舒适性影响较小。

5 结论

采用分层式控制框架设计的适用于无人驾驶车辆的ACC 系统，上层控制器考虑了前车的加速度变化，能更快响应前车动态变化；下层控制器通过改进的车辆逆纵向动力学模型进行设计。通过MATLAB/Simulink 与CarSim 联合仿真平台对完整ACC 系统进行仿真模拟，结果表明：车辆在前车从起步到定速工况下能快速控制车辆响应达到最终控制目标并保持稳定状态；在前车平稳变速工况与前车急变速工况下巡航车辆能针对前车车速变化快速响应，且在ACC 系统工作过程中始终保持良好的跟踪精度，使实际车间距与期望车间距误差较小且前后车相对速度范围较小，保证无人驾驶车辆行驶安全性。基于MPC算法的分层控制策略能在多种行驶工况下较好实现车辆的自适应巡航功能且保证车辆行车安全。