结构化道路智能车辆换道轨迹规划

于江山，杨正才，蔡林

（1.湖北汽车工业学院，湖北 十堰 442002；2.东风商用车技术中心，湖北 武汉 430000）

近年来，智能车辆的换道轨迹规划受到业内人士关注［1］。为实现智能车辆自主安全换道，轨迹规划要满足车辆动力学、运动学和环感障碍物等约束条件，同时规划的轨迹能在当前的跟踪控制方法下实现车辆实际行驶轨迹与之逼近。Chee［2］等通过统计分析实车试验数据，提出了基于梯形加速度函数规划车辆紧急换道轨迹方法，孙浩［3］等提出将微观轨迹规划问题抽象为不同终点约束换道行为的方法，并提出能够同时满足行驶安全和全局性能最优的动态轨迹规划方法，这2类方法适合简单的交通环境，但对于复杂的交通环境存在局限性。Kuwate［4］等提出了基于快速探索随机树法的实时运动轨迹规划算法，Mouhagir H［5］等将可行驶的区域均等地划分成栅格进行采点，借助特定曲线将栅格点衔接获得特定轨迹曲线，该类轨迹规划方法能够找到有效的换道轨迹，但是对于轨迹的优劣没有进行过多的比较，有些轨迹会导致方向上的震荡问题。Shibata［6］等提出了基于速度势场的避让轨迹规划方法，产生的轨迹比较平滑，但是存在局部最优解的问题。Keller［7］等用弹性带方法规划车辆避让的最佳轨迹，考虑了车辆动力学约束、道路边界约束等，轨迹具有良好的适应性，但该理论中随机点的选取会使生成的轨迹具有随机性。上述文献中提出的方法取得了一定的理论成果，但面对实时多变的动态环境和多样化的避让轨迹时，复杂的安全约束边界条件对轨迹规划效率的影响考虑得较少。文中针对智能车辆在结构化道路的换道问题，提出了碰撞锥［8］与鲸鱼优化算法（whale optimization algorihm,WOA）相结合的换道轨迹规划方法，基于自车速度和周围车辆速度、位置等信息的感知，在多项式换道轨迹基础上，利用碰撞锥方法，获取换道车辆安全性的约束条件，然后建立目标优化函数，通过WOA在约束条件下求解最优换道轨迹。

1 结构化道路场景下换道轨迹模型

车辆换道过程既要考虑道路边界条件、自主车辆的运行状态，又要考虑障碍车辆的动态运行情况，因此先分析换道过程潜在冲突区域，然后根据潜在冲突区域建立换道安全边界条件，利用多项式轨迹模型生成安全换道轨迹簇。图1 为结构化道路上车辆换道潜在碰撞典型场景，以换道车辆运动方向为X轴、垂直方向为Y轴，自主车辆换道起始时刻车身质点为坐标原点O，建立坐标系。

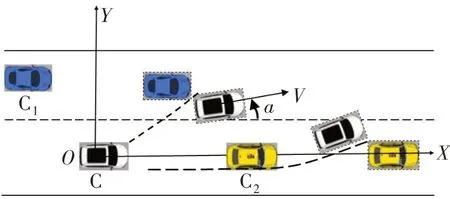
图1 典型换道场景

1.1 换道安全域

车辆在行驶过程中遇到的动态障碍物主要是汽车，因此考虑智能车辆换道问题时，基于车辆轮廓特征，忽略汽车垂直方向的运动，把自车和其他交通车辆聚类成矩形，并用外接圆包裹处理。根据碰撞锥原理［8］，自车与其他交通车辆的避让问题转换成圆与圆之间的避让问题。典型的换道场景如图2所示，自车C的外接圆半径为R，车辆C1的外接圆半径为R1，车辆C2的外接圆半径为R2。利用碰撞锥原理［8］，将自车C 与车辆C1、C2的避让问题分别等效为具有相同初始条件下圆O与圆E、圆F之间避让问题，如图3所示。

图2 车辆聚类处理示意图

图3 车辆碰撞锥模型

图4为自车C 与车辆Ci的碰撞场景图，自车避撞安全行驶速度矢量集［8］可表示为

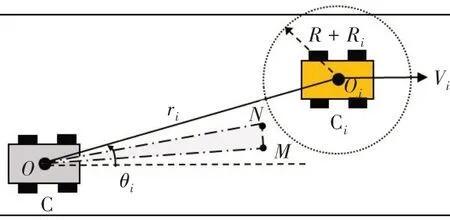
图4 车辆之间的碰撞几何学图

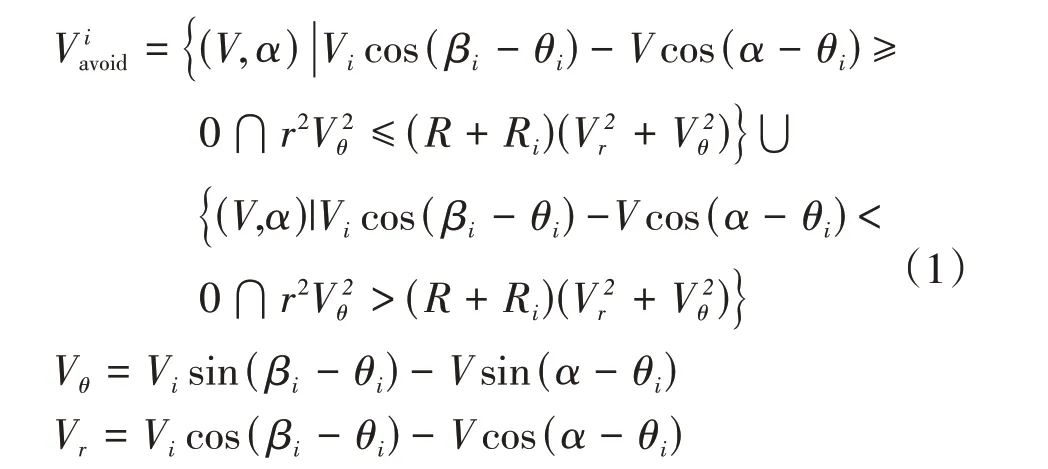
式中：α为自车避让速度方向与X轴的夹角；V为自车避撞的行驶速度；Vi为自车传感器探测到车辆Ci的速度，βi为车辆Ci速度方向与X轴形成的角，取0°；θi为直线OOi与X轴的夹角；ri为直线OOi的距离；R为自车聚类处理后的外接圆半径；Ri为车辆Ci聚类处理后的外接圆半径；Vθ为自车与Ci垂直于直线OOi的相对速度；Vr为自车与Ci沿直线OOi的相对速度。除碰撞锥（锥形NOM）之外的区域为自车C避让车辆Ci的候选速度区域。

式中：φi为车辆Ci与自车C形成的锥角，φ1为∠GOH的1/2，φ2为∠MON的1/2；θ1为直线OO1与X轴之间的夹角；θ2为直线OO2与X轴之间的夹角；w1为自车C 与车辆C1横向距离（取1 个车道宽度）；l1为直线OO1的长度；R和Ri分别为自车C 和车辆Ci聚类处理后的圆半径。

根据式（1）～（2），自车换道安全行驶域可表示为式（3），示意图如图5所示。

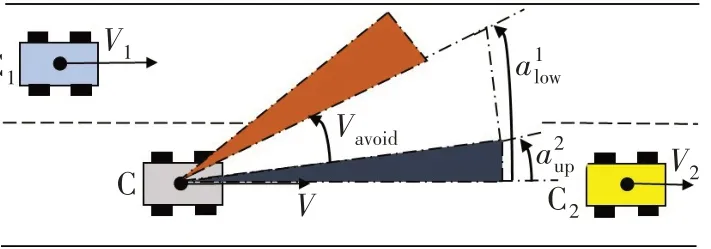
图5 换道安全域

1.2 换道轨迹簇模型

通过对实际换道轨迹的分析，发现五次多项式曲线能较好地拟合汽车换道轨迹［9-10］，符合多数驾驶者的行为习惯，同时表达式简洁。以自车质心所在位置为坐标原点，速度方向为X轴建立坐标系。考虑到换道时航向角较小，侧向速度很小，假设换道过程中纵向速度不变，侧向速度与横向速度相等。换道横向轨迹用换道时间t表示为

2 目标优化函数

智能车辆换道除了确保安全避障外，还应使车辆具有良好乘坐舒适性，即车辆换道过程中应尽可能保证车辆运行平稳。

2.1 安全性评价函数

自车换道过程中，如图5 所示，自车离同车道前车C2横向方向距离越远，要求自车航向与X轴形成的夹角越大；自车与左侧目标车道上的车辆C1距离越远，要求自车航向与X轴形成的夹角越小，因此自车航向角在上述2 个边界的中间范围为理想的安全行驶域。为减小换道安全性评价指标与舒适性指标的数量级差异，引入补偿函数h(α)，即

2.2 侧向稳定性评价函数

以换道过程中最大瞬时侧向加速度作为侧向稳定性评价函数Pc（t），即

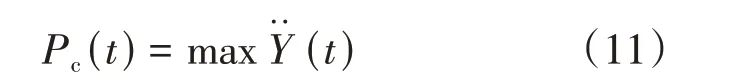
在路径规划后的跟踪控制过程中，为了保证跟踪过程的稳定性，避免换道过程中自车发生侧滑，需要满足动力学约束。由于侧向加速度受到发动机、轮胎、地面等多方面的限制，要求车辆纵横向耦合力不能超出摩擦圆约束［11］。文献［12］表明，最大侧向加速度值不会超过0.4g。为了降低计算复杂程度，将车辆模型简化为点质量模型进行计算，侧向稳定性约束条件为

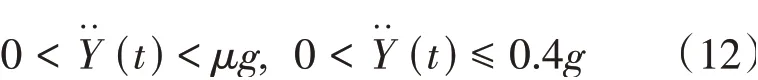
式中：μ为路面附着系数；g为重力加速度值。

2.3 目标优化函数

式（6）中，要确定五次多项式规划路径，需要确定参数值te，te与避撞安全性和侧向稳定性有关，因此将换道路径规划问题转化成相应变量在约束范围内的安全性和稳定性指标综合最优问题。目标优化函数表示为

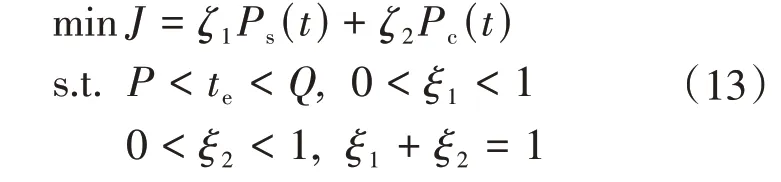
式中：P和Q分别为换道时间最小临界值和最大临界值；ζ1、ζ2分别为安全性和舒适性评价权重。在换道安全域内，根据不同换道场景确定各性能目标之间的优先级，权重值赋予不同的取值。

3 换道轨迹仿真分析

以图5所示的换道场景为例，设结构化道路的单车道宽度为3.75 m，路面附着系数为0.8，换道初始和结束状态分别为

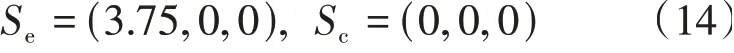
3.1 基于WOA的换道轨迹求解

WOA是模拟海洋中座头鲸捕食行为的新型群智能优化算法，结构简单，参数少，全局收敛性强且易实现［13］。根据SONG Xiao-Lin［14］等对于车辆换道时间数据集的统计和分析，式（12）的约束条件为

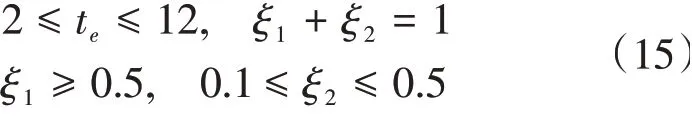
换道过程中首要目的是避免碰撞，因此假设安全性目标优先级高于稳定性目标，取ξ1为0.6，ξ2为0.4。以智能车辆某2次换道数据为例，同车道前车宽度为1.68 m，左后侧车辆宽度为1.7 m，换道工况参数如表1所示。

表1 换道工况参数

利用WOA 对目标函数进行求解，与文献［15］中提出的遗传算法进行对比。设种群规模为40，最大迭代次数为100；交叉概率为0.7，变异概率为0.1。2 种算法均在前30 次迭代中收敛，如图6 所示，可以看出，2种工况下WOA和遗传算法都能在最大迭代次数范围内收敛，迭代稳定后的目标函数值大小接近，但达到稳定时经历的迭代次数相差较大，与遗传算法相比，WOA 迭代次数更少，优化过程耗时更短，在轨迹规划时实时性更强。选取WOA 迭代稳定后的结果，工况1 目标函数值为0.76、规划的换道时间为7.5 s，工况2 目标函数值为1.2、规划的换道时间为3.2 s，设2种工况下最优换道轨迹分别为Y1(t)和Y2(t)，表达式为

图6 不同算法结果对比

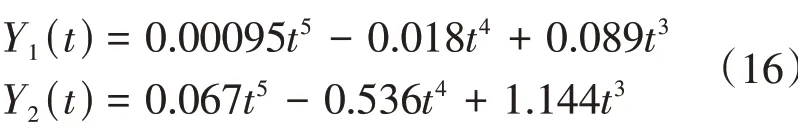
3.2 CarSim/Simulink仿真平台验证

为了验证文中提出的轨迹规划方法的可靠性，基于图5所示场景，使用CarSim中的车辆动力学模型，并为自车添加2个环感传感器获取障碍车辆信息；在Simulink中搭建碰撞锥模型、WOA模块和模型预测控制（model predictive control，MPC）模块，进行联合仿真。仿真工况如表1所示，自车动力学模型采用CarSim 中自带的B-Class Hatchback 车型，具体参数如表2所示。

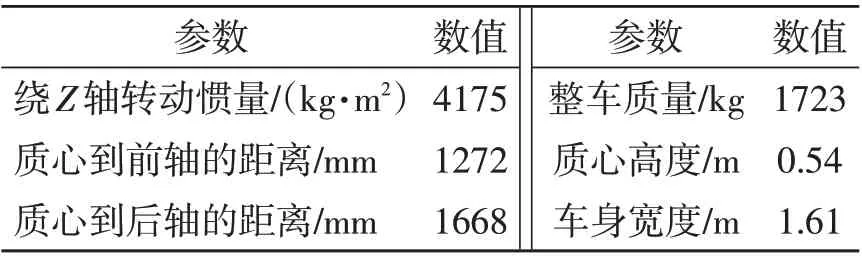
表2 自车动力学参数

图7为自车与障碍车辆的纵向距离变化曲线，可以看出，2 种工况下，在相应的换道时间内都实现避让前车和左后车辆，并保持一定的安全距离；与前车距离为负数表示自车换道后已经实现超车。图8为位移和横摆角跟踪曲线，显示实际轨迹与规划轨迹贴合较好，工况1位移跟踪误差不超过0.07 m，工况2 位移跟踪误差不超过0.1 m；横摆角时域响应及时，工况1最大横摆角为4.3°，工况2最大横摆角为5°，车身姿态稳定。从图9可知，2种工况下侧向加速度最大值都未超过4 m·s-2，均在摩擦力约束范围内，避免了因地面附着力不足而产生侧滑侧翻风险。上述结果显示碰撞锥模型与WOA相结合规划的轨迹能实现车辆安全、平稳换道。

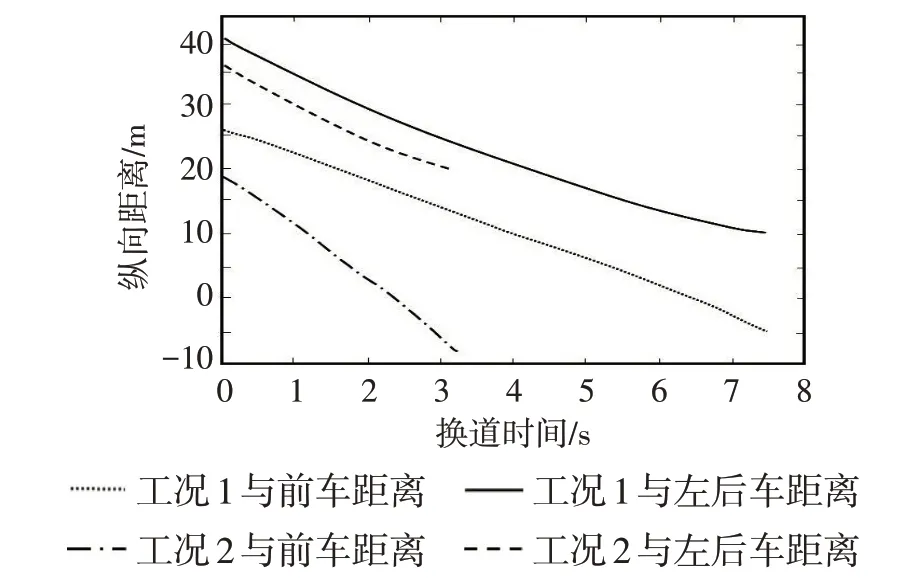
图7 自车与障碍车辆距离变化曲线

图8 位移和横摆角跟踪曲线

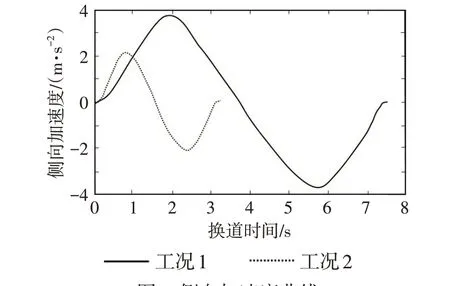
图9 侧向加速度曲线

4 结论

利用碰撞锥原理设计了结构化道路的换道轨迹规划模型，获得换道安全域，然后结合五次多项式，获得车辆安全换道轨迹簇。基于车辆运动学和动力学原理，设立换道车辆安全性评价指标和稳定性评价指标，搭建目标优化函数和约束条件，运用WOA从轨迹簇中筛选安全性和稳定性评价指标综合最优的轨迹，并将WOA与遗传算法对比，仿真结果表明WOA 需要的迭代次数更少，实时性更强。在规划的轨迹基础上，利用模型预测控制方法跟踪参考轨迹，联合仿真实验结果表明车辆行驶状态参数平稳，轨迹偏差最大不超过0.1 m，对不同的车速和转向轨迹具有较好的鲁棒性。