CMA-REPS区域集合预报随机动能后向散射方案敏感性试验*

范宇恩 李红祺 陈 静 徐致真 陈法敬 邓 国

1 四川省气象探测数据中心，成都 610072 2 高原与盆地暴雨旱涝灾害四川省重点实验室，成都 610072 3 中国气象局地球系统数值预报中心，北京 100081 4 灾害天气国家重点实验室，北京 100081 5 复旦大学大气与海洋科学系，上海 200438

提 要： 模式中常应用水平扩散项以抑制非线性计算不稳定或阻尼虚假短波，但这会导致数值模式在截断尺度附近出现小尺度动能过度耗散。为了将被过度耗散的小尺度动能补偿回模式，将随机动能后向散射扰动方法(stochastic kinetic energy backscatter，SKEB)引入CMA-REPS区域集合预报系统。首先基于由一阶自回归随机过程在水平方向上进行球谐函数展开得到的随机型，然后计算由数值扩散方案引起的局地动能耗散率，进而构造随机流函数强迫，并将其转化为水平风速扰动，对耗散的动能进行随机补偿。开展了2018年9月、10月(选取1日、7日、13日、19日、25日)的10 d集合预报随机型时间及空间尺度敏感性试验，并对试验结果进行评估。获得如下结论：在CMA-REPS区域集合预报中应用SKEB方案，可在一定程度上补偿过度耗散的小尺度动能，进而改善了模式对实际大气动能谱的模拟能力。就集合预报技巧改进而言，SKEB方案可以显著改善区域模式水平风场U、V的离散度，同时水平风场、温度等要素连续分级概率评分(CRPS)和离群值评分均获得改善。对SKEB方案开展的6个时间尺度(失相关时间尺度τ选取1、3、6、9、12、15 h)和6个空间相关尺度(最大截断波数Lmax选取80、100、120、160、200、240)敏感性试验结果表明，12 h失相关时间尺度和最大截断波数为240空间相关尺度的集合概率预报技巧更优。结论证明 SKEB方案可以补偿在截断尺度耗散的小尺度动能，有效提高集合预报技巧。

引 言

大气运动是具有混沌特性的非线性动力系统，因此初始条件或模式的微小误差会使得单一确定性数值预报模式存在不确定性(Lorenz，1965)，Epstein(1969)和Leith(1974)为了解决这种不确定性而提出了集合预报的概念。集合预报通过一定的数学方法获得在一定初值误差范围内的初值集合，对每个初值积分得到一组预报，进而估计数值预报不确定性。这种方法使确定性预报转变为概率预报，使得天气预报更加可靠，因此它是数值预报未来演变发展的一个重要方向。

根据数值预报误差来源，集合预报技术主要分为初值扰动技术和模式扰动技术。因为只依靠初值扰动技术会使集合预报存在一些不足：集合成员不够发散；集合预报系统可靠性不足；不能表现出在次网格尺度物理过程参数化所造成的不确定性等，因此Palmer et al(2005)认为模式扰动技术可以弥补现有的初值扰动技术的缺点。而现有模式扰动技术可分为多模式组合法、多物理过程组合法和随机物理扰动法。其中，随机物理扰动法是一种更为合理且复杂的模式扰动方法。随机物理扰动法在模式的某些参数值或倾向项、扩散项上引入一个随机过程或因子对其改变，以体现模式的不确定性。它是目前国际上集合预报模式扰动技术研究的重要方向(Buizza et al，1999；Shutts，2005；Jankov et al，2017)。

数值模式中常应用水平扩散项以抑制非线性计算不稳定或阻尼虚假短波，但这会导致数值模式在截断尺度附近出现小尺度动能过度耗散，如果能通过一种方案将被过度耗散的小尺度动能补偿回模式，则有可能会提高集合预报质量。为此，国外学者对此做出一些研究，并取得了较好的效果，Shutts(2005)首次将随机动能后向散射扰动(stochastic kinetic energy backscatter,SKEB)应用于集合预报，利用具有一定时空相关特征的随机型以及局地动能耗散率，在模式预报方程中引入随机流函数强迫和温度强迫，对扩散过程、重力波阻和深对流等参数化方案中存在的能量耗散进行补偿，结果表明，SKEB不仅增加了集合预报系统的离散度，并提高了概率预报技巧。Berner et al(2009)对SKEB方法中随机型进行改进，随机型基于水平方向上的球谐函数展开，并使用一阶自回归过程(马尔科夫随机过程)进行谱系数随时间的演变。由这种方法得到的随机型具有可任意调整的时空相关特征，进而可实现对随机扰动场空间尺度大小以及时间相关特征的控制。Charron et al(2010)和Tennant et al(2011)也在其研究中加入SKEB方案，引入了可调整的时空相关特征的随即型，取得较好的效果。

但是，目前国内应用较多的还是多物理过程组合法，对于SKEB模式扰动方法的研究较少。陈静等(2003)分析了不同积云对流参数化方案对华南暖区暴雨数值预报的不确定性影响，进行了集合预报试验，并证明了多物理参数化方案组合法能够反映华南暴雨预报的不确定性，具有较高应用价值。谭燕和陈德辉(2007)和张涵斌等(2014)基于CMA-REPS区域集合预报进行试验，证明了多物理参数化方案组合法能够提高集合预报效果。而在随机参数化方案的研究中，袁月等(2016)基于CMA-REPS区域集合预报进行试验，引入随机扰动参数化倾向方案(stochastically perturbed parameterization tendencies，SPPT)，其研究表明SPPT方法能有效提高集合预报离散度和概率预报技巧。王明欢等(2021)和王婧卓等(2021)在其相关研究中，均在区域集合预报系统中引入SPPT方案作为模式扰动技术。除了常见的多物理过程组合法和SPPT方法以外，不少学者在区域集合预报的参数化方案中引入了随机参数扰动SPP方法，也取得了较好的效果(徐致真等，2019；陈雨潇等，2020；熊洁等，2021)。

国内针对SKEB方案也展开了研究，彭飞等(2019)将SKEB方案引入CMA的全球集合预报，结果表明SKEB方案提高了全球集合预报的概率预报技巧。彭飞等(2020)发现联合使用SPPT与SKEB方案时，扰动对误差的描述能力最好。张涵斌等(2019)发展了一种多物理过程组合与SKEB相结合的混合模式扰动方法，结果表明SKEB方法及在其基础上建立的混合模式扰动方法具有较好的应用前景。

为了探究SKEB方案是否能提高CMA-REPS区域集合预报的质量，本文将过度耗散的小尺度动能补偿回模式，研究SKEB模式扰动方法对CMA-REPS区域集合预报扰动质量和整体预报性能的影响，并开展随机型时间及空间尺度敏感性试验，为改进CMA-REPS区域集合预报的预报质量提供依据。

1 资料和方法

1.1 CMA-REPS区域集合预报模式简介

本文采用CMA-REPS区域集合预报系统，系统的参数配置如表1所示。模式的水平分辨率为0.1°×0.1°，模式积分步长为60 s，水平格点数751×501，垂直坐标采用地形追随高度坐标，垂直层次为51层，集合预报成员数为14个集合扰动成员和1个控制预报成员，共15个集合成员，模式的初值扰动采用动力降尺度方法，初值扰动和侧边界扰动由中国气象局数值预报中心T639全球集合预报提供。集合预报试验检验所需要的等压面要素纬向风U、经向风V、温度T、高度H来自区域模式的同化分析场。

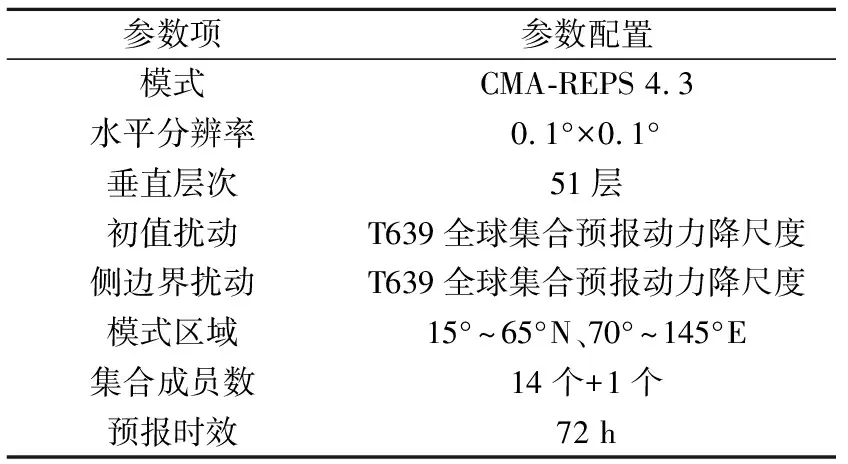
表1 CMA-REPS区域集合预报系统参数配置Table 1 Parameter configuration of CMA-REPS regional ensemble prediction system

1.2 SKEB方法原理及算法设计

1.2.1 随机型计算方法

本文的SKEB方法的随机型是参照Li et al(2008)提出的随机型产生方案，其理论基础是对基于一阶自回归随机过程(即一阶马尔科夫链随机过程)在水平方向上进行球谐函数展开，并定义随机型ψ(λ,φ,t)，如式(1)所示：

(1)

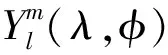
(2)

式中：Δt为CMA-REPS模式的积分步长，即60 s；τ是随机型的失相关时间尺度；Rl,m(t)是满足方差为1、均值为0的高斯分布的随机数。因此，式(1)中的随机型ψ(λ,φ,t)也具有高斯分布特征，σ是随机型ψ(λ,φ,t)的标准差。

为了控制随机型的变化范围，在式(1)和式(2)中引入拉伸函数S(ψ,μ)，得到随机型Ψ(λ,φ,t)，如式(3)所示：

Ψ(λ,φ,t)=μ+S(ψ,μ)[ψ(λ,φ,t)-μ]

(3)

本文采用的拉伸函数S(ψ,μ)参考了Li et al(2008)和袁月等(2016)使用的拉伸函数：

(4)

式中：β是常数，这里取经验值1.37。μ=(Ψmin+Ψmax)/2，其中Ψmin，Ψmax分别随机型Ψ(λ,φ,t)的最小值、最大值。引入拉伸函数是为了能设定变化范围，拉伸后的随机型Ψ(λ,φ,t)相比于未拉伸前的随机型ψ(λ,φ,t)在指定范围内变化更为均匀。

1.2.2 局地动能耗散率计算方法

Berner et al(2009)研究认为数值扩散方案导致的动能耗散足以表示动能总耗散，因此本文参照Charron et al(2010)的研究，只考虑CMA-REPS区域模式中由数值扩散方案导致的动能耗散，动能耗散率的计算公式为：

(5)

式中：D为动能耗散率，u，v为数值扩散方案前的风场，Δu，Δv为数值扩散方案前后风场的差值。图1展示了CMA-REPS区域模式2018年10月25日预报72 h的局地动能耗散率的空间分布以及纬向平均剖面。

由图1a可见，在水平方向上，300 hPa的动能耗散率的大值区主要分布于青藏高原南部、四川西部地区，而在500 hPa(图1b)，大值区主要分布于青藏高原南部；在垂直方向上(图1c)，动能耗散率大值区主要在30°N的300～200 hPa，对流层低层的50°N附近同样存在明显大值区。

1.2.3 流函数强迫扰动设计

参照Shutts(2005)与Charron et al(2010)的研究，本文将流函数强迫FΨ定义为：

(6)

式中：Δx代表网格距，取为模式的水平分辨率10 km，Δt取值为CMA-REPS模式的积分步长，即60 s。α为可调常数，用于控制扰动大小，η为表示为高度。

为了将流函数强迫转化为适合CMA-REPS区域集合预报模式的水平风场扰动，即在模式的预报方程中引入由Su，Sv表示的倾向项：

(7)

(8)

如果加入旋转风分量扰动，基于流函数与水平风场的旋转分量之间的关系，由式(7)和式(8)演变得到的旋转风分量扰动：

(9)

(10)

此外，如果加入辐散风分量扰动，Su，Sv表示为：

(11)

(12)

式中a为地球半径。在本文中，采用的是式(9)和式(10)的旋转风分量扰动。

2 SKEB随机型时间尺度敏感性试验

2.1 试验方案设计

根据国外学者研究进展可知：不同学者引入的SKEB方案采用的随机型有所差异。例如，Charron et al(2010)使用的失相关时间尺度τ为3 h；Tennant et al(2011)使用SKEB方案的随机型的失相关时间尺度τ为6 h；不同的τ值会对集合预报系统性能的影响是不同的，τ值越大，意味两个时次之间随机场相关性就大，随时间变化频率就越低。因此，本文将对SKEB方案的随机型Ψ(λ,φ,t)的失相关时间尺度τ进行敏感性试验，选取最适用于CMA-REPS的SKEB方案的参数，并为CMA-REPS的模式扰动技术升级提供科学依据。

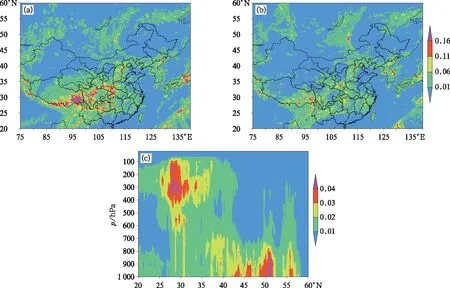
图1 CMA-REPS区域模式2018年10月25日预报72 h的局地动能耗散率分布(a)300 hPa，(b)500 hPa，(c)纬向平均剖面Fig.1 Distribution of 72 h local kinetic energy dissipation rate predicted by CMA-RPES regional model on 25 October 2018(a) 300 hPa, (b) 500 hPa, (c) zonal average profile

本文随机动能后向散射随机型敏感性试验中，首先对随机型Ψ(λ,φ,t)的失相关时间尺度τ选取六组不同的取值，以此开展包括控制试验共七组集合预报试验，以期找出最适用于CMA-REPS的参数，SKEB方案差异的具体细节详见表2。控制试验不采用SKEB方案，试验名为NOSKEB。七组试验的初值扰动和侧边界扰动均来自中国气象局数值预报中心T639全球集合预报统。试验时段为2018年9月、10月分别选取1日、7日、13日、19日、25日的总计10 d集合预报试验，预报时效为72 h。

表2 SKEB方案随机型时间尺度参数敏感性试验设计Table 2 Sensitivity test design of stochastic time-scale parameters for SKEB scheme

2.2 检验结果

2.2.1 大气动能谱

大量观测事实分析表明在对流层和平流层底部，大气动能谱具有如下的分布特征：在大尺度区域动能谱与波数的关系满足E∝k-3关系，过度到中小尺度区域表现为E∝k-5/3，且这种特征不随纬度、高度和季节变化(Nastrom et al，1984)。因此，将模式的动能谱分析特征与实际大气动能谱分布规律进行定量分析比较，可以有效地评估预报模式的预报性能。图2给出了SKEB_12 h与NOSKEB两组方案分别在24、48、72 h预报时效的10 d试验平均的大气动能谱分布。

图2a中，横轴底部是使用了归一化波数，顶部是波长，纵轴是动能谱，在大尺度区域中，SKEB_12 h和NOSKEB较为重合，但是过渡到中小尺度动能谱随波数下降过快，动能谱的斜率较观测结果(k-5/3)偏小，对中小尺度区域动能谱模拟不足，故不能体现出动能谱与波数k-5/3成正比的关系。而SKEB_12 h方案的动能谱在中小尺度区域都明显高于NOSKEB方案，且更加靠近观测结果(k-5/3)。这表明SKEB_12 h方案能够在一定程度上改善了CMA-REPS区域模式在中小尺度区域对实际大气动能谱的模拟能力。

2.2.2 集合离散度和RMSE

对于一个可靠的集合预报系统而言，理论上集合离散度与均方根误差(RMSE)保持一致，但在实际的集合预报系统中，离散度不够发散。因此，离散度应该保证足够的大，以至于预报集合能包含大气真值。

图3a～3c是各个层次的纬向风的离散度和均方根误差变化特征随预报时效的演变，由图可见，七组试验的RMSE随着预报时效的演变基本保持一致，但是250 hPa和500 hPa的SKEB_12 h方案的RMSE略低于NOSKEB控制预报，低层850 hPa中，SKEB_9 h方案的RMSE较低。与此同时，引入SKEB方案的试验组都提高了离散度，其中SKEB_12 h方案的离散度是七组试验中最高的；综上说明，失相关时间尺度τ取值为12 h时，SKEB_12 h方案构造的模式扰动相较于NOSKEB方案能提高集合预报质量；对于温度(图3d～3f)，在250 hPa和500 hPa的，七组试验的RMSE随着预报时效的演变基本保持一致，在低层850 hPa，引入SKEB方案的RMSE低于控制预报，其中 SKEB_9 h的效果较好，SKEB_12 h和SKEB_15 h次之。离散度方面，所有引入SKEB方案的试验组都提高了离散度，且SKEB_12 h方案和SKEB_15 h方案的离散度是七组试验中较高的，但是对温度的离散度改进没有纬向风的离散度提升明显，这与SKEB方案没有对温度的耗散量进行补偿有关。

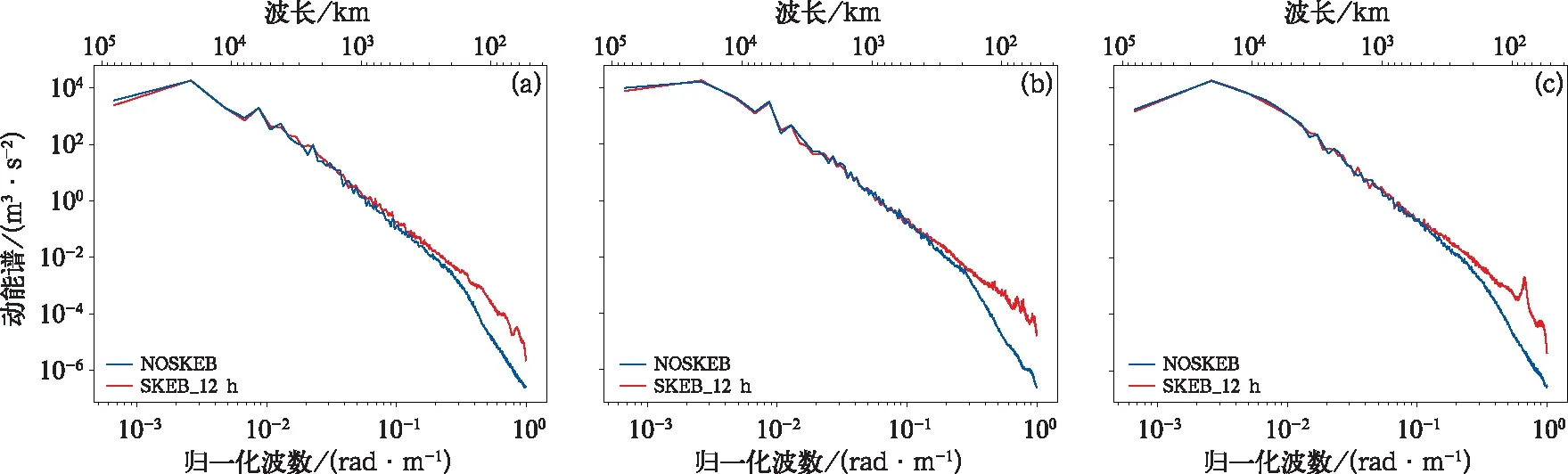
图2 SKEB_12 h方案与NOSKEB方案的2018年9月和10月的1日、7日、13日、19日、25日(共10 d)平均的大气动能谱分布(a)24 h,(b)48 h,(c)72 hFig.2 The 10 d average atmosphere dynamic energy spectral distribution of the entire layer in September and October 2018 in SKEB_12 h test and NOSKEB test (a) 24 h, (b) 48 h, (c) 72 h

图3 时间尺度敏感性试验结果(a,b,c)U,(d,e,f)T的离散度和均方根误差变化特征随预报时效演变(a，d)250 hPa，(b，e)500 hPa，(c，f)850 hPa Fig.3 The spread and root mean square error of (a, b, c) U and (d, e, f) T of the time-scale sensitivity test result as a function of forecast lead time(a， d) 250 hPa， (b， e) 500 hPa， (c， f) 850 hPa

综上所述，引入SKEB方法能够有效提高离散度，提高集合预报质量，在时间尺度敏感性试验中，且SKEB_12 h方案的对集合预报技巧的改善效果最好。

图4a和4b分别给出NOSKEB和SKEB_12 h方案10 d试验结果在72 h的500 hPa纬向风离散度水平分布，为了比较两者的差异，从图4c可知，SKEB_12 h方案提升离散度的主要区域为深红区域，降低离散度的区域为蓝色区域，而图4c中大部分区域都为红色区域，这说明SKEB_12 h方案能对CMA-REPS区域模式提升较多离散度。

2.2.3 连续分级概率评分

连续分级概率评分(CRPS)能够定量比较预报累计分布概率与观测累计分布概率差异，能够衡量概率预报性能，CRPS值越小表示集合预报系统的概率预报性能越好。图5是控制试验七组试验的纬向风和温度的CRPS评分随预报时效演变，对于纬向风(图5a～5c)，七组试验的CRPS值在高层250 hPa 和中层500 hPa中，SKEB_12 h的值较低且低于控制预报NOSKEB；而在低层850 hPa纬向风，SKEB_9 h的CRPS评分较低。而对于温度(图5d～5f)，在高层250 hPa和中层500 hPa中，SKEB_12 h和SKEB_15 h略低于控制预报NOSKEB，而在低层850 hPa，CRPS评分的改进效果优于中高层，其中SKEB_9 h和SKEB_12 h的CRPS评分较低。

图4 (a)NOSKEB方案和(b)SKEB_12 h方案的10 d平均的72 h预报的500 hPa纬向风离散度及(c)两个方案的差值Fig.4 The U spread at 500 hPa of the 10 d average forecast for 72 h of (a) NOSKEB test and (b) SKEB_12 h test and (c) the difference between them

图5 同图3，但为CRPS评分Fig.5 Same as Fig.3, but for the CRPS

综上所述，SKEB方案对CRPS评分的改进效果有限，SKEB_12 h方案对CRPS评分的改进效果最好。

2.2.4 离群值

离群值(outlier)指观测落在集合预报成员之外的频率，是衡量集合预报可靠性的一种评分，其值越低，说明集合成员预报分布越可靠。由图6a～6c可见，引入SKEB方案的六组时间尺度敏感性试验相比较于控制预报NOSKEB均显著降低了各个层次纬向风的outlier评分，其中SKEB_12 h方案的离群值减小最显著，例如在预报时效36 h，outlier评分减小幅度为14.9%，这说明SKEB_12 h方案使得区域集合预报包含实况的可能性更高，集合预报质量更优；同样，引入SKEB方案的六组敏感性试验均显著降低了温度的离群值评分(图6d～6f)。

对于高层250 hPa温度，SKEB_9 h和SKEB_15 h方案的离群值减小较为显著；对于中层500 hPa温度，SKEB_12 h方案的离群值减小最显著；低层850 hPa 温度，SKEB_12 h和SKEB_15 h方案离群值减小较为显著。

综上所述，SKEB方法可有效显著降低outlier评分，使集合成员预报分布更加可靠，提升集合预报质量，在时间尺度敏感性试验中，且SKEB_12 h方案的对集合预报技巧的改善效果最好。

3 SKEB随机型空间尺度敏感性试验

3.1 试验方案设计

本文第二部分对随机型ψ(λ,φ,t)的失相关时间尺度τ进行敏感性试验，总结得出SKEB_12 h试验的对预报技巧提升效果最优。而对于空间尺度敏感性试验，与最大截断波数有关。不同学者在引入的SKEB方案采用的随机型最小、最大截断波数有所差异。Tennant et al(2011)使用SKEB方案的随机型的最小、最大截断波数分别是5、60；Charron et al(2010)使用的SKEB方案的随机型的最小、最大截断波数分别是40、128。Tennant et al (2011)与Charron et al (2010)的研究中，使用的模式均为全球模式，构造的集合预报系统与本文使用的CMA-REPS区域集合预报系统有较大的差异。因此，本文将对SKEB方案随机型的最大截断波数进行敏感性试验，选取最适用于CMA-REPS的SKEB方案的参数。

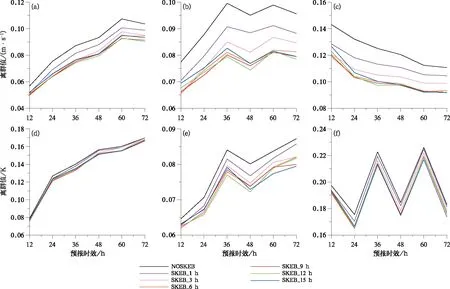
图6 同图3，但为离群值评分Fig.6 Same as Fig.3, but for the outlier

本节基于时间尺度敏感性试验结果，对随机型ψ(λ,φ,t)的空间尺度进行敏感性试验。为了避免引入大尺度扰动，固定最小截断波数Lmin为20，再分别选取最大截断波数Lmax为80、100、120、160、200、240的六组试验，加上控制预报NOSKEB共七组集合预报试验，以期找出最适用于CMA-REPS的参数，SKEB方案差异的具体细节详见表3。NOSKEB不使用SKEB方案。七组试验的初值扰动和侧边界扰动均来自T639全球集合预报系统。试验时段为2018年9月、10月分别选取1日、7日、13日、19日、25日的总计10 d的集合预报试验，预报时效为72 h。

表3 SKEB方案随机型空间尺度参数敏感性试验设计Table 3 Sensitivity test design of stochastic spatial-scale parameters for SKEB test

3.2 试验结果

3.2.1 集合离散度和RMSE

图7a～7c是各个层次的纬向风的离散度和均方根误差变化特征随预报时效的演变图，由图可见，七组试验的RMSE随着预报时效的演变基本保持一致，SKEB_100的RMSE略低于控制预报NOSKEB；而从离散度方面分析，引入SKEB方案的试验组都提高了离散度，高于控制预报NOSKEB，方案SKEB_240 的离散度是七组试验中最高的，说明最大截断波数Lmax为240时，扰动振幅较大，提升离散度较高，但是会影响到RMSE；对于温度(图7d～7f)，七组试验的RMSE随着预报时效的演变基本保持一致；但是在低层850 hPa，引入SKEB方案会明显的降低RMSE，且SKEB_240的RMSE较低；而离散度方面，所有引入SKEB方案的试验组都提高了离散度，由于没有直接补偿温度的耗散量，所以离散度提升效果并不明显，综合比较各个方案，SKEB_160方案的离散度是七组试验中最高的。

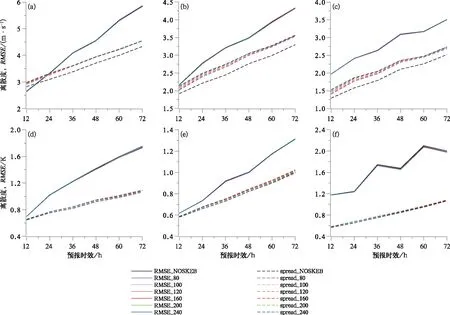
图7 空间尺度敏感性试验结果(a,b,c)U和(d,e,f)T的离散度和均方根误差变化特征随预报时效演变(a，d)250 hPa，(b，e)500 hPa，(c，f)850 hPaFig.7 The spread and root mean square error of (a, b, c) U and (d, e, f) T the spatial-scale sensitivity test result as a function of forecast lead time (a， d) 250 hPa， (b， e) 500 hPa， (c， f) 850 hPa

3.2.2 连续分级概率评分

图8是控制试验七组试验的纬向风和温度的CRPS评分随预报时效演变图，对于高层纬向风(图8a)和中层纬向风(图8b)，引入SKEB的各个方案对CRPS评分的改进效果有限，SKEB_100和SKEB_120的CRPS值较低；而对于低层纬向风(图8c), SKEB_240对CRPS评分有一定的改进效果，且低于控制预报NOSKEB；对于温度(图8d～8f)的CRPS评分，七组试验的CRPS值在高层250 hPa 和中层500 hPa基本保持一致；SKEB_240方案对低层850 hPa温度CRPS评分改进效果最好。

综上所述，引入SKEB方案对CRPS评分的改进效果有限，最大截断波数Lmax为240时，对CRPS评分的改进效果最好。

3.2.3 离群值

对于纬向风(图9a～9c)，引入SKEB方案的六组空间尺度敏感性试验均显著降低了各个层次纬向风的outlier评分，其中SKEB_200和SKEB_240方案的离群值减小较为显著。另一方面，对于高层250 hPa温度(图9d)，SKEB_160方案的离群值减小最显著；对于中层500 hPa温度(图9e)，在预报时效36 h前，SKEB_200方案的离群值减小最显著，随着预报时效延长，SKEB_120方案的离群值减小最显著。对于低层850 hPa温度(图9f)，在预报时效36 h前，SKEB_200方案的离群值减小最显著，随着预报时效延长，SKEB_120试验的离群值减小最显著。

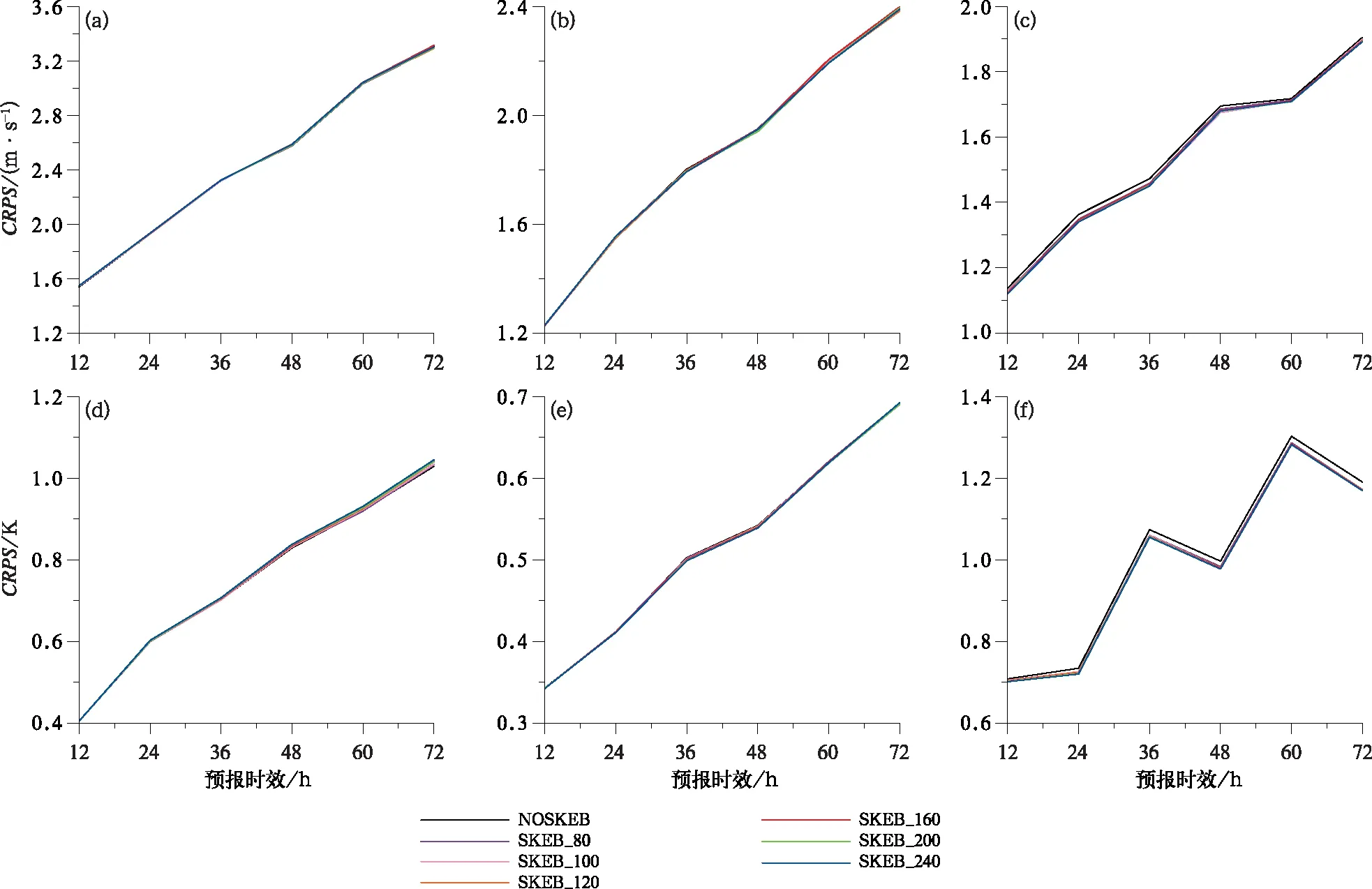
图8 同图7，但为CRPS评分Fig.8 Same as Fig.7, but for the CRPS

图9 同图7，但为离群值评分Fig.9 Same as Fig.7, but for the outlier

综上3种评分，在空间尺度敏感性试验中，最大截断波数Lmax会直接影响到扰动振幅大小，因此对于被扰动的纬向风U来说，SKEB_240方案的对集合预报技巧的改善效果最好。而对于没有被扰动的温度T，各个方案之间差距不明显，SKEB_240方案稍微较好一点。

4 结论与讨论

为了描述区域模式在次网格能量转化过程中存在的不确定性，本文将SKEB方法引入CMA-REPS区域集合预报系统，以期体现次网格尺度能量升尺度转换过程中存在的模式误差，进一步增加集合离散度，并提高概率预报技巧。本文采用一阶自回归随机过程在水平方向上进行球谐函数展开得到的随机型，计算了由数值扩散方案引起的局地动能耗散率，以随机型和局地动能耗散率构造了随机流函数强迫，并根据流函数与水平风速旋转分量之间的关系，将SKEB方案中的随机流函数强迫转化为适用于CMA-REPS的水平风速扰动。开展了集合预报试验和随机型时间及空间尺度敏感性试验，从大气动能谱、集合离散度与集合均方根误差、CRPS评分、离群值评分客观分析评估方面，较为系统地考察了SKEB方法对CMA-REPS区域集合预报的影响。结果表明：

(1)在CMA-REPS区域集合预报中应用SKEB方案，可在一定程度上补偿过度耗散的小尺度动能，进而改善了CMA-REPS模式对实际大气动能谱的模拟能力。就集合预报技巧改进而言，SKEB方案可以显著改善区域模式水平风场和温度的离散度，同时水平风场、温度等要素连续分级概率评分(CRPS)和离群值评分均获得改善。

(2)开展了集合预报试验和随机型时间及空间尺度敏感性试验，选取6个时间尺度(失相关时间尺度τ选取1、3、6、9、12、15 h)和6个空间相关尺度(最大截断波数Lmax选取80、100、120、160、200、240)。试验结果表明，最大截断波数Lmax会直接影响到扰动振幅大小，τ值影响扰动的形态，失相关时间尺度τ=12 h和最大截断波数Lmax=240时，集合概率预报技巧更优。

(3)SKEB方案没有直接对温度T的耗散量进行补偿，在时间尺度敏感性试验中，SKEB方案对温度的各项评分有一定的改进效果，SKEB_12 h方案表现较好；而在空间尺度敏感性试验中，SKEB方案对温度的各项评分改进效果不明显，各种SKEB方案之间差距不大。