压榨机关节轴承镶嵌孔设计及分析
王海龙,曹 均,黄海波,文静波
(1.宁波大学机械工程与力学学院,浙江 宁波 315211;2.芜湖美达机电实业有限公司,安徽 芜湖 340201)
1 引言
压榨机关节轴承是压榨机的重要组成部分,在低速、重载等复杂工况中轴承容易发生摩擦磨损导致损坏。早在上世纪五十年代,各学者针对轴承摩擦磨损等问题进行了研究[1],分别提出了喷油润滑,制备二硫化钼、尼龙涂层,润滑脂润滑等一系列方法,压榨机关节轴承处于复杂工况环境中,工作温度短期超过100 ℃,负载超过200 T,在大功率和温升环境,上述研究难以满足压榨机关节轴承长效使用要求。油润滑轴承需要庞大的润滑系统进行冷却和过滤,但润滑油粘度和润滑性能受高温影响,在压榨机工作过程中容易受到水分、固体颗粒的污染造成润滑失效从而导致压榨机关节轴承发生故障[2-4]。文献[5]对关节轴承聚四氟乙烯润滑涂层进行了设计和研究,结果表明轴承润滑性能得到了提高,但聚四氟乙烯的耐磨性较差,无法满足压榨机关节轴承大功率和长寿命工作的要求。文献[6]通过欧洲AK45试验方法在不同温度下对润滑脂轴承进行实验,得出温度越高润滑脂寿命越低,且当环境温度从20℃上升至80℃时润滑脂寿命相比20℃时下降(95~97)%,无法满足压榨机轴承实际工况要求。
目前,对于压榨机关节轴承自润滑研究主要集中在镶嵌固体自润滑物上,在工作过程中固体润滑材料在内外圈摩擦时受到挤压形成微小的磨粒,磨粒随着摩擦副滑移在表面形成固体转移膜,从而降低摩擦因数和轴承合金的磨损量[7]。文献[8]对镶嵌孔进行了研究,基于单孔的圆柱壳模型提出了应力公式;文献[9]研究在不同厚度的壳体上开孔对基体承载能力的影响,以上研究均未对具体的孔径、深度和分布比例影响进行系统研究。文献[10]采用垂直镶嵌方法对镶嵌深度为8mm孔的关节轴承进行了研究,指出镶嵌结构能有效地降低轴承摩擦因数,但研究并未对镶嵌比例及镶嵌深度等变量进行研究。文献[11-12]基于传统镶嵌孔比例经验,对轴承进行镶嵌结构研究,对于深度变量和分布未进行深入研究。文献[13]通过摩擦因数分析提出(23~63)%的镶嵌比例为最优结果,但未分析结构强度和疲劳强度寿命。文献[14]研究了孔深和孔径单个变量对轴承的应力分布影响。文献[15]在此基础上研究了两种不同的孔径和深度对轴承的影响,但对于镶嵌孔分布比例和分布缺乏细致的研究。
压榨机关节轴承镶嵌孔径、比例、深度和分布未系统研究,针对现有国内外研究现状和压榨机关节轴承长效工作寿命要求,采用固体润滑镶嵌方法,深入研究镶嵌孔径、比例、深度和分布对关节轴承应力和寿命影响,设计(4~10)mm 四种不同的镶嵌孔径、(15~40)%镶嵌面积比例和(3~12)mm四种不同的镶嵌深度对应力分布和寿命的影响。通过仿真计算确定最佳孔径、深度和镶嵌比例;最后以不同轴承为例,采用相同研究方法,通过对比和结果分析,验证设计结果的正确性。
2 轴承镶嵌设计分析
2.1 轴承介绍
利用三维建模软件UG 8.0建立模型,轴承在轴线方向对称安装,为提高计算效率,建立的1/4模型,如图1所示。其中轴承外圈外径290mm,高58mm,内圈外径250mm、内径200mm,

图1 轴承1/4模型Fig.1 1/4 Model of the Bearing
高67.5mm,轴长167.5mm。轴承外圈和销轴材料为轴承钢(GCr15),内圈材料为铜合金(QBe2),轴承材料参数,如表1所示。

表1 材料参数Tab.1 Material Parameters
2.2 镶嵌比例分析
轴承镶嵌比例是轴承性能的重要影响因素,镶嵌比例过小则润滑性能不佳,镶嵌比例过大则无法满足压榨机关节轴承重载使用要求。为方便加工,在轴承内圈外表面设计镶嵌孔,在相同动载荷作用下,由于向心镶嵌孔抵抗弹塑性变形能力优于垂直镶嵌孔[16],因此采用向心镶嵌结构,如图2所示。

图2 内圈镶嵌方式图Fig.2 Mosaic Pattern of the Inner Ring
关节轴承完整内圈外径∅250mm,高度135mm,外表面总表面积为S=33750πmm2。基于外表面积设计6组镶嵌比例,分别为15%、20%、25%、30%、35%、40%。按照相同排列方式对内圈外表面进行镶嵌,开孔排列方式和比例,如图3所示。设计轴承轴向交错排列,径向通过改变每排之间的锥度来改变镶嵌比例,保证在轴承转动时固体润滑剂在径向运动方向与相邻孔均有切向交叠,从而实现整个摩擦接触面均匀润滑。

图3 内圈镶嵌比例图Fig.3 Mosaic Ratio of the Inner Ring
基于ANSYS Workbench 有限元的仿真,首先对轴承外圈和端面施加固定约束,对轴承内外圈接触面、轴与内圈接触面建立frictional接触对,并设定非对称接触;定义轴承内圈外表面和轴凸面为接触面,定义轴承外圈内表面和内圈内表面为目标面。为提高计算精度和模拟实际工况,设定限制接触面不能穿透目标面,并对轴承内圈、外圈和销轴的接触摩擦面进行网格细化处理。对压榨机关节轴承模型的对称面设置frictionless support无摩擦对称约束(面的法向约束),对外圈外表面施加compression only support仅有压缩的约束(限制的面在法向正方向移动)。压榨机关节轴承径向承受962.5kN的载荷,轴向承受8.75kN载荷。
对内圈进行镶嵌比例分析。镶嵌位置及镶嵌孔形状相同,研究压榨机关节轴承内圈最大等效应力和最大应力变形随镶嵌比例变化的规律,并分析最佳镶嵌比例。如图4所示,随着镶嵌比例的增加,内圈最大等效应力和最大应力变形总体呈现出增长的趋势,(15~20)%阶段的最大等效应力数值大小平均相差0.895%,最大应力变形数值大小平均相差0.45%,(20~40)%阶段最大等效应力和最大应力变形急剧增加,数值大小平均增加24.91%和10.21%。

图4 内圈应力和变形曲线Fig.4 Stress and Deformation Variation Curve of the Inner Ring
镶嵌比例20%的内圈最大等效应力和最大应力变形最小。当镶嵌比例为20%时内圈最大等效应力和应力变形发生跳跃,且镶嵌比例20%的数值小于15%的值,这是因为15%镶嵌比例的孔在轴承内圈外表面分布不对称,20%镶嵌比例的孔为均分结构,且金峰[17]研究也表明开孔相错布会造成结构不对称发生扭曲,从而降低结构的承载能力。从分析结果可知镶嵌比例为40%时,轴承的等效应力最大,这是因为镶嵌孔数目较多,内圈的结构发生了较大改变,导致轴承承载能力下降。因此,镶嵌比例20%的内圈承载能力最强。
2.3 镶嵌孔深度分析
为研究不同镶嵌孔深度对内圈最大等效应力和最大应力变形的影响,根据研究的最佳镶嵌比例设计内圈外表面的镶嵌深度依次为3mm、6mm、9mm、12mm。
受人口持续增加、经济高速发展的影响,流域排污量大,水体污染严重。全流域开展监测的48条河道(段)824km河长中,165km水质基本好于V类,其余河道(段)基本为劣V类,流域水质状况远远不能满足水体功能要求。
在轴承轴端面径向施加962.5kN的载荷,轴向施加8.75kN载荷,镶嵌位置、形状和大小相同,研究内圈最大等效应力和应力变形随镶嵌深度变化规律,并分析最佳镶嵌深度。
随着镶嵌孔深度的增加,内圈最大等效应力和最大应力变形呈现增长趋势,且等效应力分布在6mm深度后出现急剧增加现象,镶嵌深度为(3~6)mm 的内圈最大等效应力和最大应力变形最小,如图5所示。轴承镶嵌孔直径与镶嵌深度比(径厚比)影响轴承的应力和寿命。
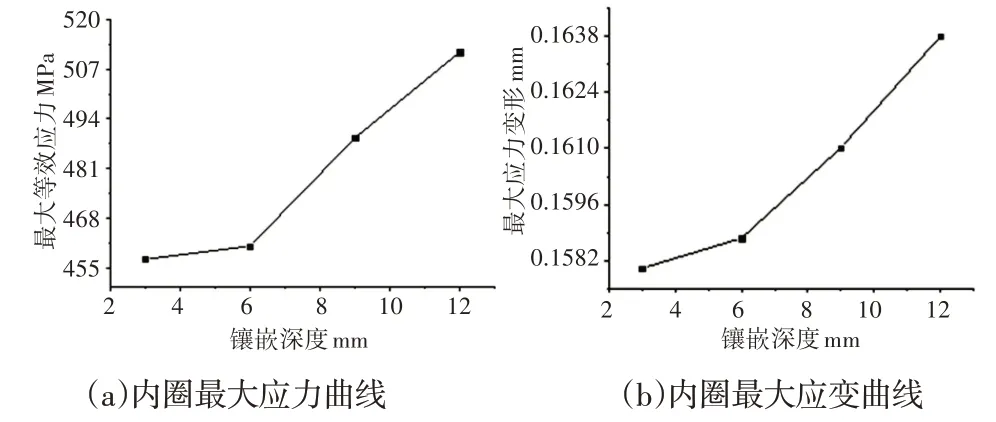
图5 内圈应力应变曲线Fig.5 Stress-Strain Variation Curve of the Inner Ring
根据分析结果可知最大等效应力和应力变形随径厚比的减小而逐渐增大,当镶嵌深度为(3~6)mm时,最大等效应力和应力变形增长相对平缓,增长了0.75%和0.47%,但在6mm深度之后应力和变形迅速变大。
当镶嵌深度达到9mm时,靠近轴承内圈轴向两边孔的深度已经接近轴承本身的厚度,造成薄弱处敏感度加剧,内圈应力和变形迅速变大,相对于6mm深度的数值增长了5.8%和1.4%。当镶嵌深度达到12mm时,轴承承载能力最低且等效应力最大。镶嵌深度太浅,潜藏固体润滑物容易脱落,考虑嵌藏固体润滑物的镶嵌牢固性和长久使用性,因此6mm为最佳深度。
2.4 镶嵌孔径分析
为研究不同镶嵌孔径对内圈最大等效应力和最大应力变形的影响,根据研究的最佳镶嵌比例和镶嵌深度,依次设计镶嵌孔孔径大小,对比分析不同开孔孔径的内圈最大等效应力和最大应力变形的变化规律。
设计开孔半径依次为4mm、6mm、8mm和10mm,如图6所示。

图6 不同镶嵌开孔的内圈Fig.6 Inner Rings with Different Inlay Holes
由图7 可知,最大等效应力随径厚比(d/h)的增大呈现先减小后增大的趋势,且在0.64处达到最小。其中d为开孔直径,h为内圈最大厚度,对同一轴承进行开孔分析,当内圈最大厚度相同时,径厚比(d/h)与开孔孔径成正比关系。

图7 不同径厚比的应力变化曲线Fig.7 Stress Variation Curve Under Different Diameter-Thickness Ratio
径厚比变化为(0.32~0.64)时,内圈最大等效应力随径厚比的增大而减小,此时镶嵌孔径减小,开孔数量增加,内圈等效应力和变形受轴承开孔间距影响,间距减小会降低内圈承载能力[18]。当径厚比为0.64且开孔孔径为8mm时,内圈承载能力达到最大值。孔间距增大,内圈开孔处应力分布主要受孔径影响。孔径越大,在孔附近的峰值应力越大,且易产生应力集中,降低内圈承载能力。
3 接触疲劳理论分析
压榨机关节轴承在工作中不断承受交变载荷,容易发生疲劳失效,基于内外圈材料的S-N曲线和疲劳寿命理论分析计算镶嵌轴承的寿命,如图8所示。

图8 内外圈S-N曲线Fig.8 S-N Curve of the Inner and Outer Ring

第n个交变应力损伤分量为:

则压榨机关节轴承总损伤为:

压榨机关节轴承在所有循环交变作用下可以承受的总周期为:

压榨机关节轴承疲劳寿命为:

镶嵌比例为40%的轴承外圈疲劳循环次数均为107,为高周疲劳,内圈最低疲劳循环次数为2.443×105,如图9可知,上述设计满足压榨机关节轴承使用要求。在开孔位置满足径向方向孔与孔之间有一定的交叠,同时,在孔表面存在应力集中,因此,开孔位置应尽可能地远离内圈边缘。

图9 轴承疲劳寿命Fig.9 Fatigue Life of the Bearing
由图10、图11可知,通过对比最大等效应力和最大应力变形可知外圈最大等效应力和最大应力变形均发生在内表面的左上角边缘处。

图10 应力云图Fig.10 Nephogram of Stress

图11 变形云图Fig.11 Nephogram of Deformation
镶嵌设计的内圈最大等效应力和最大应力变形均分布在外表面上半部分右上角边缘处。镶嵌设计的轴承内外圈的最大等效应力均比未镶嵌的轴承大,这是因为镶嵌开孔破坏了内圈外表面结构的连续性,降低了内圈的承载能力,但等效应力均在允许的范围之内,未出现屈服破坏现象,因此,设计满足压榨机关节轴承使用要求。
4 验证分析
文献[19]研究的9000kN平锻机的轴承,镶嵌比例20%和开孔半径7.6mm为最佳工程应用方案,为验证本文设计,选用闵显文论文的轴承模型进行计算分析和对比。模型,如图12所示。其中轴承内圈外径360mm、内径315mm,高120mm,轴长270mm。内圈外表面总面积为S=37800πmm2。为满足9000kN平锻机的要求,在轴承轴端面上径向施加2750kN载荷,轴向施加25kN载荷,其它条件不变。

图12 轴承1/4模型Fig.12 1/4 Model of the Bearing
由图13可知,内圈最大等效应力和最大应力变形随着镶嵌比例的增加而增大,镶嵌比例(15~20)%之间最大等效应力和应力变形增长缓慢且数值仅增加1.36%和0.58%,镶嵌比例(20~40)%之间最大等效应力和应力变形增加超过17.66%和6.22%。图13中15%镶嵌比例的轴承内圈最大等效应力最小,结果与上文中20%镶嵌比例的轴承内圈最大等效应力最小不同,但镶嵌比例为20%的轴承最大等效应力和最大应力变形与15%的轴承应力和变形数值差异仅为1.36%和0.58%,进一步分析发现闵显文研究中的轴承镶嵌孔分布靠近轴承边缘,在轴承工作时开孔处出现局部应力集中现象导致20%镶嵌比例的轴承内圈最大等效应力激增,由于应力变化仅1.36%,且镶嵌比例越大轴承摩擦系数越小,20%的镶嵌比例优于15%。

图13 镶嵌半径8mm内圈等效应力及变形曲线Fig.13 Equivalent Stress and Deformation Variation Curve of the Inner Ring Under 8mm Radius
由图14 可知,随着镶嵌深度的增加,内圈最大等效应力和最大应力变形总体呈现出增长的趋势,由于内圈等厚且厚度为22.5mm,当镶嵌深度达到12mm时不会出现内圈太薄而产生敏感部位,因此,等效应力和应力变形近似等比例增大,如图15所示。其中d为开孔直径,h为内圈最大厚度,径厚比(d/h)为(0.36~0.72)时,内圈最大等效应力随着镶嵌孔径的增大而减小,随着镶嵌孔径的减小,开孔数量急剧增加,开孔间距减小,导致内圈最大等效应力增大。径厚比(d/h)为0.72时内圈最大等效应力达到最小,随着径厚比的增大,最大等效应力开始增大。对于同一个轴承进行不同孔径的镶嵌设计,当开孔半径为8mm 时径厚比为0.72时,内圈最大等效应力为最小,因此,开孔半径为8mm为最佳镶嵌孔径。在相同面积上镶嵌相同比例的镶嵌孔,半径8mm的孔需要236 个,半径6mm 的孔需要420 个,半径4mm 的孔需要945个,考虑加工工艺的复杂性,满足内圈承载能力的同时,半径8mm的孔设计最优。

图14 内圈应力应变曲线Fig.14 Stress-Strain Variation Curve of the Inner Ring

图15 径厚比-应力变化曲线Fig.15 Variation Curve of the Diameter-Thickness Ratio-Stress Change
通过不同尺寸的轴承对比分析,内圈最大等效应力和应力变形曲线变化趋势相似,最大等效应力随着开孔孔径的增大呈现出先减小后增大的趋势,且在孔半径8mm处达到最小。
得出镶嵌比例20%、镶嵌孔半径8mm为最优结果,证明了这里方法的正确性。文献论文中提出最佳设计方案应用到实际工况中,镶嵌轴承寿命相比未镶嵌轴承提高了(5~6)倍。同时考虑镶嵌固体润滑物的镶嵌牢固性及钻孔的成本问题,选6mm为最佳镶嵌深度。
5 结论
针对关节轴承镶嵌孔径、比例、深度和分布未系统研究的问题,这里以大型压榨机自润滑关节轴承为例,采用有限元分析计算方法,研究了关节轴承内圈不同开孔孔径、镶嵌比例、镶嵌深度的最大等效应力、最大应力变形和疲劳寿命,通过不同尺寸的轴承分析对比,验证了这里研究的结果准确性,并得出以下结论:
(1)镶嵌比例为20%为最优分布比例,此时轴承镶嵌孔对称分布,轴承等效应力最小,疲劳寿命最长。镶嵌比例为20%时的孔分布结构对称。
(2)镶嵌深度在(3~6)mm时等效应力和变形增长平缓,6mm后随着深度增加,轴承承载能力急剧下降,导致应力和变形迅速增长。镶嵌深度于镶嵌润滑物体积正比,综合考虑6mm深度为最优设计结果。
(3)在镶嵌比例20%、镶嵌深度6mm时镶嵌孔半径为8mm内圈的最大等效应力最小。内圈最大等效应力与孔径近似成对号函数关系,因此8mm为最佳镶嵌孔径。

