基于CSAR图像的目标高度提取方法

李一石， 陈乐平， 安道祥， 冯 东， 周智敏

(国防科技大学电子科学学院， 湖南长沙 410073)

0 引言

圆周合成孔径雷达(Circular Synthetic Aperture Radar，CSAR)作为一种新体制SAR模式，与以传统直线轨迹SAR模式相比，CSAR是通过360°全方位观测角度获得高分辨图像的三维合成孔径雷达成像系统。CSAR利用雷达在方位-高度平面上沿圆形轨迹运动，从而在方位向和高度向合成孔径来获得第三维分辨率，从而实现对场景区域的三维成像。CSAR成像技术相对于直线SAR成像技术而言，其最大的优势在于CSAR在某一高度上做圆周运动，且波束始终指向观测场景区域，所以能够更多地获得目标的全视角特征数据。

在三维信息获取方面，在CSAR模式下，由于位于成像参考平面的点目标，在不同方位角观测时，投影到成像高度平面的不同位置，造成全孔径成像的畸变，可以利用单帧子孔径图像的相关性与差异性获得场景的高程信息。

ONERA在2012年提出了根据子孔径图像序列提取观测场景数字高程模型(Digital Elevation Model，DEM)的方法，并对获取的罗马竞技场X波段机载实测数据进行处理，并利用所得数据成功提取到了场景的DEM。实验结果对这一理论进行了实际验证，实测数据的测量精度达到了1.5 m。

中科院电子所对这一类方法进行了进一步的研究，给出了CSAR模式下直接获取DEM的具体方法，并且给出了弧长划分、子孔径匹配以及目标三维位置解算的依据。最后通过微波暗室实验验证了该方法的可行性。

西电的张金强等人利用子孔径之间的特性提出了联合相关法，将CSAR圆周数据划分成若干圆弧，将每段圆弧内的所有子孔径进行相关计算，并引入了由AFRL公布的Gotcha实测数据进行实验验证。然而，该方法在计算每段圆弧内全部子孔径的相关性时产生的计算量过大，由于划分圆弧时，圆弧之间存在大部分的重叠，导致子孔径图像之间的相关信息产生大量的重复计算；并且，随着子孔径之间方位角的增大，子孔径之间的相关性也会降低，会融入更多相关性较低的数据，影响整体结果，并且处理的实验场景高程范围较小，对于高程范围较大的场景可能不适用。

针对上述问题，本文对利用子孔径特性的这一类方法进行了改进和创新，提出了一种新的提取DEM方法，提高子孔径之间的相关系数，更为合理地调用子孔径。最后引入了自主测量的实验数据对方法进行验证，实验场景更为复杂，从而验证该方法的准确性和实用性。

1 CSAR子孔径特性

CSAR模式的几何示意图如图1所示，以地面水平面为成像平面，构建空间直角坐标系。作为高度轴，雷达平台绕观测中心在高度的平面上做半径为的圆周运动。其中，雷达的波束俯仰角为，方位角为。根据分辨率的大小决定子孔径方位角的宽度，然后将整个圆周回波数据按照相同方位角宽度划分成多个相同尺寸的子孔径回波数据。根据后向投影算法(Back Projection Algorithm，BPA)对子孔径回波数据进行成像，得到子孔径图像序列。

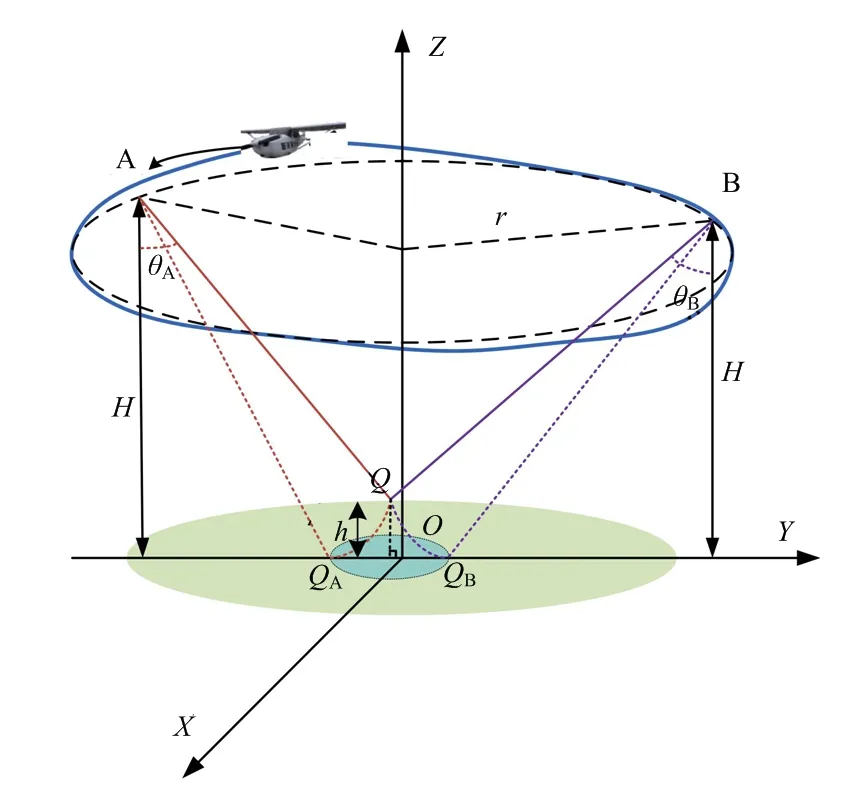
(a) 透视图

从图1中可以看出，相对于不在成像平面上的点目标，其真实位置所在的高度平面与成像平面的高度差为，这将会导致子孔径图像发生几何形变。位于不同方位角的子孔径图像，其几何形变也是不同的。点目标(A,A,Δ)在子孔径A成像投影后，设成像平面的高度为0，那么在成像平面上的坐标(A′,A′,0)为

(1)

式中，为子孔径A的方位角，为子孔径A的下视角。可以看出，子孔径图像的几何形变与点目标所在位置距成像平面的高度差有关。目标所在高度平面与成像平面之间高度差越大，子孔径图像的几何形变越大。同时，波束俯仰角和方位角也会对子孔径图像的几何形变程度产生影响。那么，点目标在子孔径B上的成像位置相对于其在子孔径A上的位置偏移为

(2)

式中，为子孔径B的方位角，为子孔径B的下视角，B′为点目标在子孔径B成像投影后，在成像平面的横坐标，B′为相对应的纵坐标。可以看出，子孔径图像间的几何形变与子孔径之间的方位夹角有关，子孔径间的方位夹角越大，子孔径之间的几何形变也会越大。同时，子孔径图像间的相关性也会随着子孔径间方位夹角的增大而降低。下面结合AFRL公布的实测数据进行验证。

对于特定的某一个子孔径方位夹角，随机选择两个子孔径成像数据并采用整幅图像和逐像素两种方式来计算二者之间的相关系数。其中，方位夹角的变化范围为0°～90°。对于每一个方位夹角，随机选择10对子孔径进行相关计算。取10组结果的平均值作为该方位夹角的相关系数结果，按照此方法计算出0°～90°所有方位夹角的相关系数，结果如图2所示。

图2 子孔径图像间相关性随方位夹角的变化关系

可以看出，在0°～90°范围内，整体呈递减趋势，子孔径图像之间的相关系数随着方位夹角的增大而减小，尽管在36°～83°，相关性系数变化略有起伏，但是相关性系数过低，低于0.5，这也会影响后面高度提取的精度。

对于逐像素的方式来计算子孔径间的相关性系数，相关性的计算公式为

(3)

式中，(,)和(,)为两个子孔径图像数据的滑块，和为滑块和内数据的平均值。滑块的大小为15像素×15像素。将所有像素的平均值作为该方位夹角的相关系数结果，按照此方法遍历0°～90°所有方位夹角，得到所有方位夹角的相关系数结果。

根据文献[9]，在方位夹角变化范围为3°～42°时，子孔径图像之间的相关系数随着方位夹角的增大而减小。这对后面子孔径划分以及方位夹角的选取提供了依据。

2 DEM提取方法

为了提高子孔径之间的相关性从而提高DEM的提取精度，本文提出了一种新的方法，并引入了新的相关性计算方式使得DEM的提取结果精度更高。在CSAR模式下，首先，将整个圆周回波数据分割成若干相互重叠的圆弧，再将圆弧划分成若干子孔径；第二，将子孔径回波数据进行BP成像；第三，将子孔径图像数据进行高度向投影；第四，对子孔径进行相关性计算，提取出单一方向的DEM结果；最后，将所有单一方向的DEM信息进行融合得到全方位的DEM结果。其流程图如图3所示。

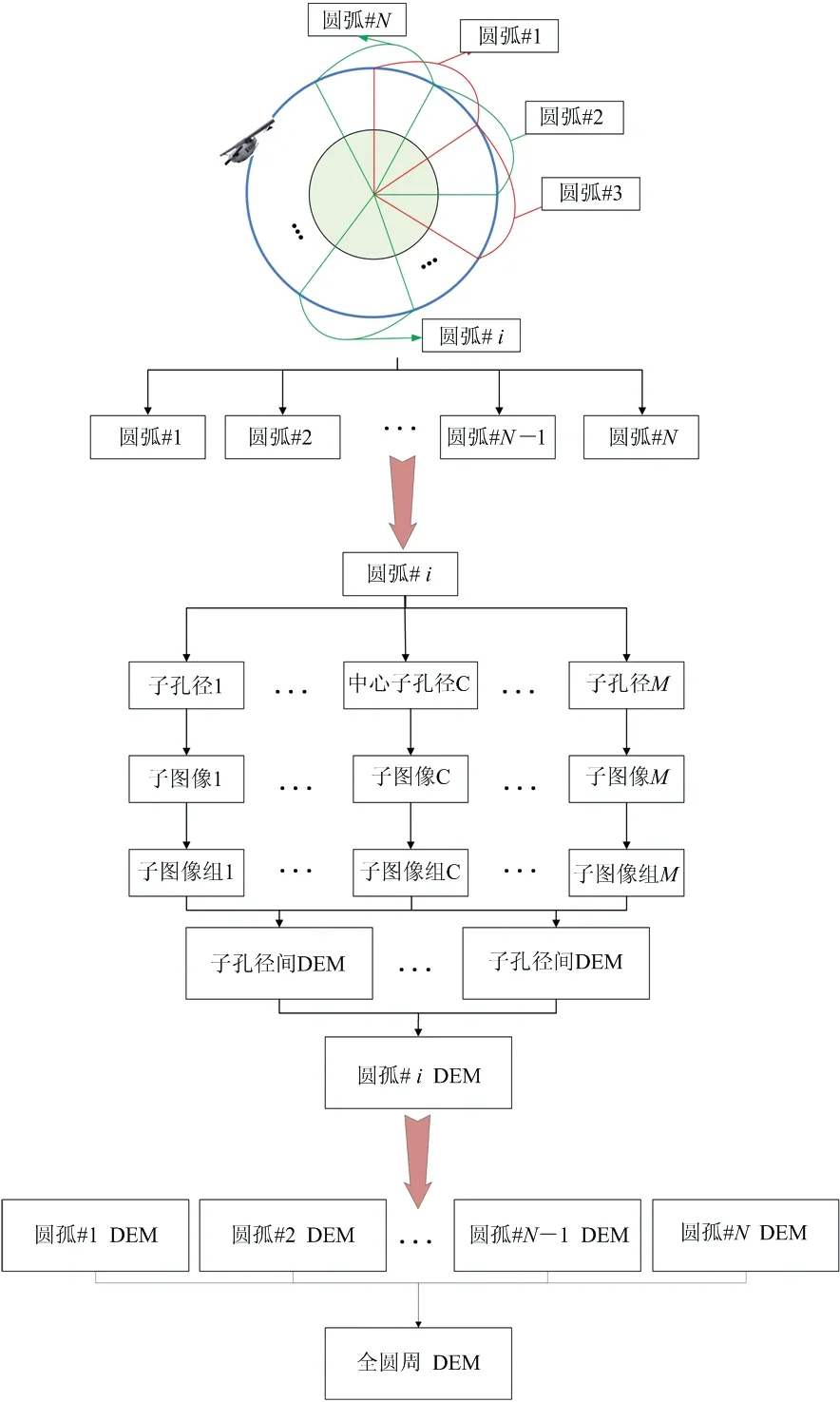
图3 目标高度提取流程图

具体步骤如下：

1) 子孔径划分。将整个圆周孔径回波数据划分成若干圆弧，每段圆弧包含若干子孔径。圆弧弧长由子孔径尺寸Δ、子孔径的数量和子孔径间的方位夹角Δ共同决定，弧长的表达式为

=Δ+(-1)×Δ

(4)

子孔径的尺寸要满足所需要的方位向分辨率，CSAR模式下的方位向分辨率Δ可以表示为

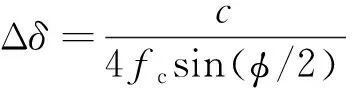
(5)

式中，为信号的中心频率，为子孔径的尺寸，为光速。

子孔径的尺寸越大，那么所包含的信息就越丰富，方位向分辨率就越高。同时，子孔径间的方位夹角越大，子孔径图像之间的相关性越弱，为保证子孔径相关系数对DEM提取的有效性和准确性，相邻子孔径间的相关系数不能低于0.5。

2) 子图像获取。对子孔径回波数据进行非相干成像处理，得到子孔径图像数据。本文采用的是后向投影算法，为了提高成像算法效率，使用了GPU并行运算进行成像。

3) 子图像高度向投影。可以将成像高度的变化对子孔径成像的影响有效地反映在高度轴上，便于后面利用相关性的差异确定目标的真实高度。首先对观测场景的高程范围进行估计，建立高度向坐标轴，然后设定合适的高度间隔，最后根据计算的坐标偏移量将子孔径图像投影到每一个高度值，形成子孔径图像组。

4) 高度信息提取。选择一段圆弧中心位置的子孔径与该圆弧上其他位置的子孔径逐一进行计算。利用高度向投影后子孔径图像组之间对应高度层的相关性，逐高度层进行计算，取相关性最强的高度层作为该处的高度结果。其中高度向逐层投影相关示意图如图4所示。子孔径之间的相关性计算公式为

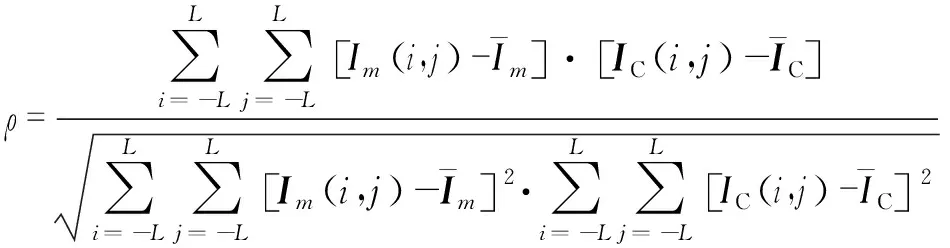
(6)

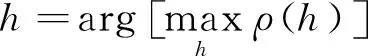
(7)

5) 高度信息融合。将圆弧上每一个子孔径与该圆弧的中心子孔径逐一进行相关性高度提取后，将提取的结果进行叠加平均，作为该圆弧的高度提取结果；按照此原则，计算整个圆周所有的圆弧，将所有圆弧的提取结果进行叠加平均，从而得到全方位的高度提取结果。

图4 子孔径高度向逐层相关示意图

3 实测数据验证

为验证本文所提算法的适用性和准确性，本实验采用L波段360°全方位CSAR数据，该数据由国防科技大学电子科学学院利用自主研制的L波段全极化SAR系统录制，实验地点在陕西省渭南市。雷达系统的天线入射角为39°，分辨率为0.5 m，成像范围为90 m×90 m。实验场景的光学地图如图5所示，360°全孔径成像结果如图6所示。

图5 观测区域光学图像

图6 观测场景CSAR图像

按照流程图，将L波段CSAR圆周数据进行划分，将每个圆弧的方位角宽度设定为60°，圆弧之间重叠角度为30°，整个圆弧共划分为11个圆弧。根据文章第2节子孔径之间的相关性与方位夹角的关系，结合分辨率的要求，将每个子孔径设定为3°，高度提取结果如图7、图8所示。

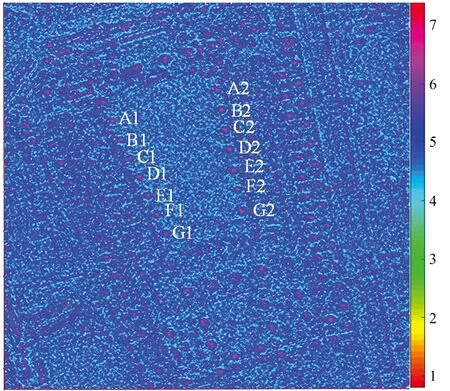
图7 实验场景高度提取结果

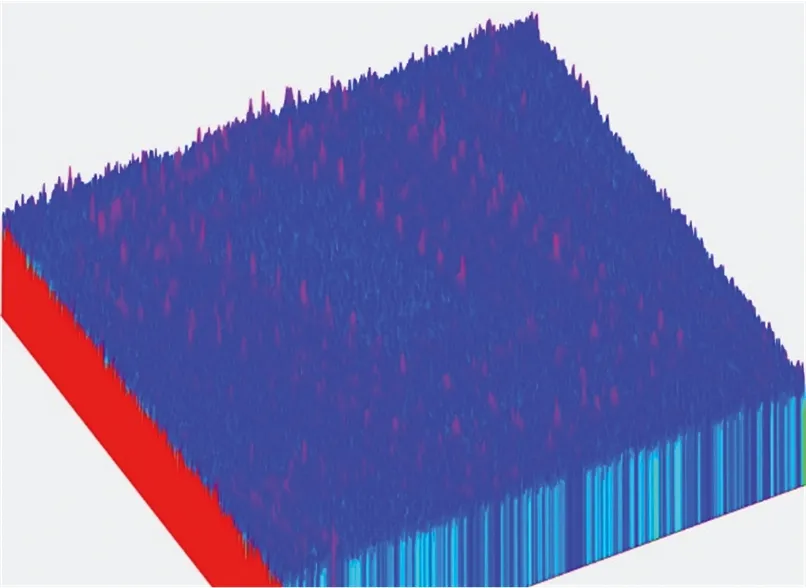
图8 高度提取结果立体图

从图中可以清楚地看出观测区域的轮廓的同时，整个图像较为清晰，噪点较少，与光学测绘的地形相匹配，DEM的三维视图与真实地形相接近。

接下来对结果进行定量分析，对场景中的路灯建筑进行高度分析，路灯建筑的光学图片如图9所示，其实际高度为6.2 m，对场景高程范围大致估计后，子孔径图像高度投影的范围为0～10 m，每一高度层间隔为0.5 m，对区域场景中的14个路灯目标高度进行计算，取目标路灯的最高的元素区域内所有像素的平均值作为该区域的真实高度，结果如表1所示。其中，实验测量高度结果在5.84～6.63 m，平均高度为6.19 m，与目标的实际高度较为接近，平均误差为0.26 m，误差较小，证实了本文所提方法的有效性。

图9 路灯实际场景图片

表1 目标路灯高度测量结果 m

4 结束语

本文提出了一种在CSAR模式下提取目标区域高度信息的方法。该方法只通过雷达系统单圈回波数据，利用子孔径图像之间的相关性和几何形变对目标高度进行提取。通过子孔径图像高度向投影以及选取圆弧子孔径与中心子孔径进行相关计算，使得高度的提取精度更高，并且绘制了目标场景的立体视图。最后，通过引入自主测得的L波段实测数据对该方法进行验证，并对实际观测目标进行对比，证实了该方法的有效性和准确性。