高地应力软岩大变形隧道洞型及双层初期支护支护时机研究

谢金池， 寇 昊， 何 川， 聂金诚， 杨文波， *， 肖龙鸽

(1. 西南交通大学 交通隧道工程教育部重点实验室， 四川 成都 610031； 2. 中国建筑股份有限公司， 北京 100044)

0 引言

随着我国“一带一路”倡议的提出，西部地区的交通建设取得了新进展。但由于地质条件复杂，在隧道建设过程中出现了越来越多的长大深埋隧道，高地应力软岩大变形问题在隧道开挖过程中比较突出。高地应力软岩隧道大变形一直是隧道施工的重大难题，高地应力软岩隧道施工围岩变形量大、变形速率快，经常发生初期支护开裂、掉块、钢拱架扭曲等现象，严重时甚至发生二次衬砌、仰拱混凝土开裂，对隧道施工安全、进度、成本造成了严重影响。

目前已有较多学者对高地应力软岩大变形隧道开展了研究。田四明等[1]针对川藏铁路雅安至林芝段的高地应力软岩大变形隧道，提出了加强主动支护、大断面机械化开挖、适时施作二次衬砌的工程举措。张金龙等[2]根据玉磨铁路景寨隧道的变形破坏特征，采用了施作径向高预应力锚索和注浆、快挖快支快封闭、少爆破开挖、改良钢架的优化措施。韩常领等[3]整理归纳了对高地应力软岩隧道变形的控制对策，并以此为基础提出了多阶段分等级协同控制变形的方法。孟陆波等[4]为探明高地应力软岩隧道非对称大变形特征，以200个高地应力软岩隧道大变形数据为基础，得出了非对称大变形的影响因素。王睿等[5]以统一强度理论为基础，推导出适用于软岩大变形隧道的围岩松动圈半径计算公式，并优化了初期支护锚杆长度。何乐平等[6]在综合分析软岩隧道大变形风险影响因素的基础上，提出针对软岩隧道大变形风险的评价指标和相应的分级标准。马栋等[7]总结了高地应力软岩隧道施工实践经验，并阐述了大变形隧道的变形特征和关键控制技术。韩常领等[8]认为采用双层初期支护后，支护结构与围岩协同变形，围岩变形分布更均匀。王仁杰等[9]通过数值模拟，提出在大跨隧道施工设计时，选择合适的隧道断面高跨比对安全施工、降低工程成本有着重要的意义。张俊儒等[10]对高地应力陡倾板岩隧道的合理洞型选择展开研究，确定了控制隧道变形的合理高跨比范围。郭新新等[11]通过模型试验及数值模拟，认为对于大断面隧道，合理的高跨比可优化围岩支护体系的受力，提高经济效益。唐雄俊[12]基于隧道约束收敛理论，提出围岩-支护作用2阶段分析思路，引入初期支护屈服轴力与围岩变形折减率作为合理支护时机的判据。周建等[13]分析了隧洞支护过程中塑性区应力、洞壁位移、支护压力的变化情况，并提出隧洞支护的合理时机。

综上可以看出，针对如何应对高地应力软岩隧道大变形的问题，目前主要是采用加强支护的手段，较少考虑洞型、初期支护支护时机对隧道围岩变形的影响。因此，本文依托华丽高速公路东马场1号隧道工程，开展高地应力软岩大变形隧道洞型及双层初期支护支护时机研究，提出高地应力Ⅲ级大变形围岩隧道合理的断面高跨比及第2层初期支护施作时机，以期为类似高地应力软岩大变形隧道洞型选择及初期支护施作时机提供参考。

1 高地应力软岩大变形隧道支护模式及围岩变形特征分析

1.1 工程概况

东马场1号隧道为2车道分离式隧道，左线全长5 098 m，右线全长5 205 m，其中，Ⅳ、Ⅴ级围岩共长7 099 m(占比达68.9%)，以泥岩和灰岩为代表的变质破碎软岩为主，具有岩体强度低、流变明显的特点，隧道地质断面图和净空断面图分别如图1和图2所示。断层两侧的岩性有较大差异，出口端是泥盆系白云质灰岩、灰岩，进口端是侏罗系泥质粉砂岩、泥岩，构造应力作用强烈，裂隙发育，呈碎块状。出口K73+860里程断面处(埋深约600 m)最大水平主应力方向为NE75°左右，与隧道未开挖段的轴线走向夹角为65°～85°，水平构造应力(16.05 MPa)大于竖向构造应力(13.79 MPa)，说明横截面原地应力场以水平构造应力为主导。

图1 东马场1号隧道地质断面图

东马场1号隧道穿越程海-宾川断裂(F3断裂带)。程海-宾川断裂属于全新世活动断裂、发震断裂，宽约95 m，长180 km，断层产状310°∠72°，属压性逆断层，多期次强烈活动，具有7级左右发震能力。隧道最大埋深为613 m，现场测得的初始地应力为16.24 MPa。综合围岩强度指标可知，东马场1号隧道处于高应力区、极高应力区，开挖过程中大变形问题突出。

图2 东马场1号隧道净空断面图(单位： cm)

1.2 大变形等级与支护结构参数

东马场1号隧道施工采用三台阶开挖工法，开挖步骤为： 上台阶弧形导坑开挖—上台阶拱部初期支护—中台阶开挖，中台阶边墙初期支护—下台阶开挖，下台阶边墙初期支护—仰拱初期支护—边墙及拱部第2层初期支护，开挖流程如图3所示。现场施工中在距离掌子面25 m左右时及时进行第2层初期支护，并要求15 d内初期支护封闭成环，在初期支护沉降收敛速率不大于0.5 mm/d(持续1周)后方可施工二次衬砌。

图3 东马场1号隧道开挖流程

隧道最初采用单层初期支护，受全新世活动的程海-宾川断裂带影响，在施工过程中，在逐渐接近断裂带的变质泥岩、变质灰岩等软岩区段时，隧道出现了大变形并且逐渐加剧，隧道结构发生了初期支护开裂剥落、拱架折叠扭曲、变形侵限、二次衬砌开裂、仰拱开裂及拱底隆起等现象，如图4所示。

(a) 初期支护开裂剥落(b) 拱架折叠扭曲

隧道未开挖段围岩主要为灰岩、泥岩，围岩破碎、强度较低。公路隧道相关规范中并没有明确对围岩大变形进行分级。参考TB 10003—2016《铁路隧道设计规范》，依据围岩的强度应力比值Rb/σmax(Rb为围岩强度，σmax为最大地应力)对围岩的大变形进行了分级，如表1所示。根据地勘资料所得的未开挖段围岩强度，确定未开挖段围岩强度应力比(如表2所示)，再结合大变形分级表与已施工段围岩变形情况，隧道设计过程中应加强应对大变形的工程措施，因此确定剩余未开挖段按照Ⅲ级大变形(强烈大变形)进行设计。

表1 《铁路隧道设计规范》大变形分级表

表2 未开挖段围岩强度应力比

为此，对未开挖段支护形式进行调整，将Ⅲ级围岩大变形(强烈大变形)段改为双层初期支护的复合衬砌结构形式，其典型断面如图5所示，具体支护结构设计参数见表3。

图5 双层初期支护典型断面图(单位： m)

表3 支护结构设计参数

1.3 双层初期支护体系下围岩变形特征

目前，东马场1号隧道断面高跨比为0.9，采用双层初期支护结构进行施工。施工过程中开展了变形监测，在拱顶设置了沉降监测点，在拱肩、拱腰设置了水平收敛监测点。

1.3.1 围岩变形

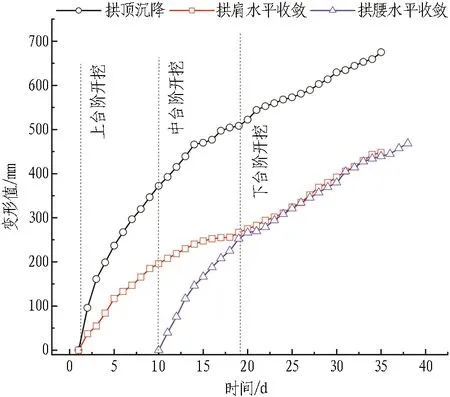
ZK73+050断面变形监测结果如图6所示。由图6可知，围岩变形特征为拱顶沉降最大，拱腰水平收敛次之，拱肩水平收敛最小；隧道施工期间以拱顶沉降为主，拱顶沉降最大值为577.1 mm，远远大于拱肩水平收敛值299.9 mm。

(a) 单层初期支护

拱顶沉降之所以远大于拱肩水平收敛，是由于按照弹性圆孔理论计算，隧道开挖后正应力减小为零，受力主要为切应力，即由原来的三向受力状态转为二向受力状态，并且受开挖工序的影响，会导致实际过程中产生应力转移的现象；同时，由于拱顶开挖后临空时间较长，导致拱顶沉降远大于拱肩水平收敛。

由图6可知： 隧道开挖后，围岩变形迅速增大，14 d时拱顶沉降为401 mm，最终变形值为577 mm； 20 d时拱肩水平收敛为210 mm，最终变形值为300 mm； 25 d时拱腰水平收敛为340 mm，最终变形值为479 mm。

采用双层初期支护与采用单层初期支护相比，拱顶沉降最大值减小了14.49%，拱肩水平收敛最大值减小了33.04%，拱腰水平收敛最大值相差不大。

1.3.2 围岩变形速率

围岩变形速率监测结果如图7所示。根据监测结果可知，双层初期支护情况下围岩变形速率较大，拱顶最大沉降速率为66.1 mm/d，拱肩最大水平收敛速率为28.8 mm/d，拱腰最大水平收敛速率为34.5 mm/d。

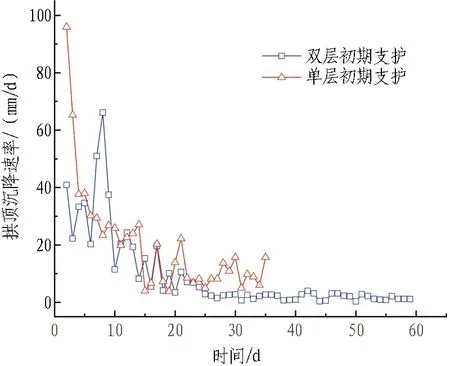
(a) 拱顶沉降速率

与采用单层初期支护相比，采用双层初期支护后拱顶最大沉降速率下降了31.07%，拱肩最大水平收敛速率下降了22.99%，拱腰最大水平收敛速率下降了16.26%。

虽然采用双层初期支护代替单层初期支护后，围岩变形和变形速率有了一定程度的减小，但在隧道初期支护仰拱封闭后还是出现了拱肩破坏、仰拱开裂等现象，如图8所示。

(a) 拱肩破坏(b) 仰拱开裂

采用双层初期支护后仍出现拱肩破坏、仰拱开裂等情况，原因是： 1)由于受到开挖工序的影响，会导致实际施工过程中产生应力转移的现象，拱顶、拱腰处的应力转移至拱肩处，导致拱肩处压应力过大(如图9所示)；另外，隧道处于高应力区、极高应力区，应力过大，隧道仰拱与隧道其他位置相比曲率较小，从结构形式方面来说不利于受力；同时，由于施作仰拱时施工整体性较差，仰拱还要承担隧道结构上部转移的力。2)第2层初期支护施作过早，第1层初期支护的预留变形量过小，导致第1层初期支护并未充分发挥承载能力。

图9 围岩压力监测结果

为此开展隧道洞型及双层初期支护支护时机研究，提出合理的隧道断面高跨比及第2层初期支护施作时机建议，以期从根本上解决高地应力软岩大变形问题，控制隧道变形，确保施工安全和施工进度。

2 高地应力软岩大变形隧道合理洞型研究

2.1 隧道断面高跨比对围岩变形的影响

高跨比又称扁平率，是隧道断面高度与隧道断面宽度之比，有开挖断面和净空断面2种情况，通常情况下按照开挖断面得出高跨比。高跨比反映了断面的扁平程度，高跨比越小，隧道断面形状越扁平[9]。

对于单线隧道一般采用高跨比较大的断面形式，以减少空间浪费。而对于双线、三线、四线的大断面隧道，随着隧道跨度增大，出于空间利用率考虑，不可避免地要降低扁平率。一般扁平率小的隧道，支护结构抵抗垂直荷载的能力明显弱于抵抗水平荷载的能力，使控制垂直方向上的围岩稳定性的难度明显大于水平方向；而扁平率大的隧道，支护结构抵抗水平荷载的能力明显弱于垂直荷载，使控制水平方向上的围岩稳定性难度要明显大于垂直方向[9]。

在破碎、较破碎的围岩中，隧道的变形主要为开挖的空间效应引起的变形。东马场1号隧道的围岩较破碎，故其围岩变形主要是开挖的空间效应引起的变形。扁平形状的大断面结构很难应对这种挤压性环境，尤其是很难保证拱部的稳定性，隧道之前的破坏特征也印证了这一点。

2.2 计算模型及参数

结合工程实际情况，采用FLAC3D软件分别建立高跨比为0.80(马蹄形)、0.90(类圆形)、1.00(圆形)的3种隧道三维模型，如图10和图11所示。

(a) 整体模型

(a) 马蹄形断面，高跨比0.80

其中，高跨比0.80的断面为原设计断面，高跨比0.90的断面为变更后的现场实际断面，高跨比1.00的断面为本次数值模拟断面。模拟采用Mohr-Coulomb强度准则弹塑性本构模型。

第1层初期支护厚度为31 cm，第2层初期支护厚度为29 cm，二次衬砌厚度为70 cm。围岩、第1层初期支护、第2层初期支护、二次衬砌采用实体单元模拟，超前小导管和锚杆采用cable单元模拟。隧道模型上台阶长5 m，中台阶长8 m，下台阶长11 m，循环进尺为1 m。

计算前模型左右施加16.05 MPa的水平构造应力，上部施加13.79 MPa的围岩自重应力(地应力测量地段为K73+860，埋深约600 m)，前后和底部施加固定约束。围岩力学参数及支护参数分别如表4和表5所示。

表4 围岩力学参数

表5 支护参数

2.3 计算结果分析

监测点布置如图12所示。取数值模拟中隧道中间位置(里程ZK73+050)的计算结果进行不同高跨比隧道开挖过程中的受力变形分析。

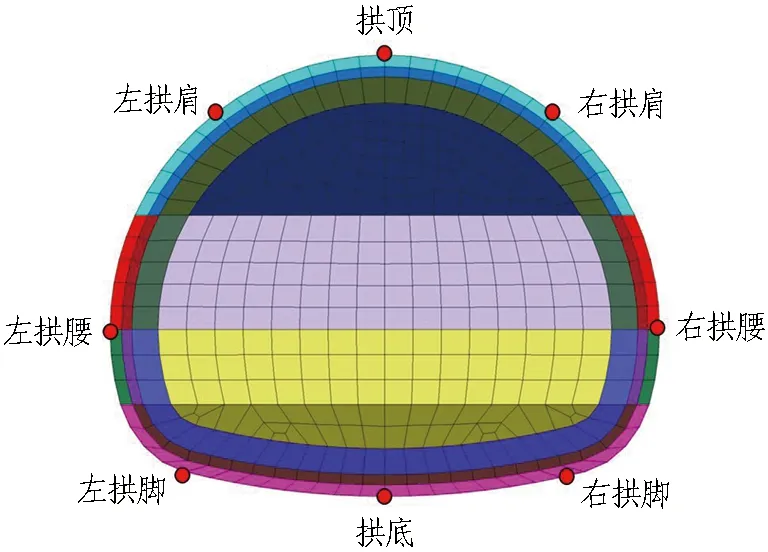
图12 监测点布置图

2.3.1 不同高跨比隧道围岩变形分析

高地应力场中3种高跨比下，从开挖到施作二次衬砌完成后的全过程中，隧道拱顶沉降，拱底隆起以及拱肩、拱腰、拱脚水平收敛随开挖步的变化如图13所示。由图可以看出，隧道高跨比为0.9时数值模拟结果与现场监测数据较吻合。

由图13可知，在开挖到目标断面(开挖步为30)前，监测点处已经发生了一定的变形；当掌子面距目标断面的开挖步小于10时，对变形的影响较为显著。在上台阶开挖时，围岩竖向位移增长速度较快；在下台阶开挖并施作上中下三台阶的初期支护后，拱顶沉降速度明显放缓；在仰拱开挖并施作初期支护后，拱底隆起的速度也明显放缓；在仰拱闭合后，拱顶沉降与拱底隆起均逐渐趋于收敛。

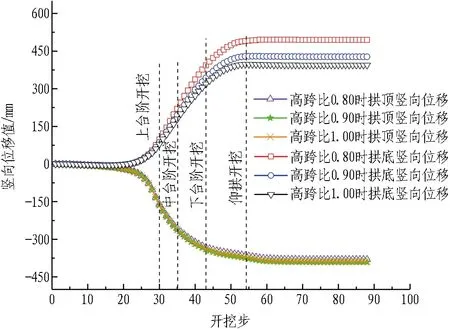
(a) 拱顶与拱底竖向位移值

在3种隧道断面高跨比下，拱顶沉降差别不大，但拱底隆起差异明显。随着隧道高跨比的逐渐增大，拱底隆起逐渐减小，高跨比为1.00时最大拱底隆起值为394.2 mm，相对高跨比为0.80时的最大拱底隆起值494.8 mm减小了20.33%。

各监测点在水平方向上都出现了向净空面方向的位移，水平方向的位移值相对竖向位移而言较小。随着高跨比的增加，拱腰水平收敛略微增加，拱脚水平收敛增加不大，拱肩水平收敛明显减小。相比高跨比为0.80，高跨比为1.00时，拱肩水平收敛最终值的绝对值从205.8 mm减小到178.7 mm，减小了13.17%；拱腰水平收敛最终值的绝对值从313.4 mm增加到328.0 mm，增加了4.66%；拱脚水平收敛最终值的绝对值从258.4 mm增加到282.8 mm，增加了9.44%。

拱肩、拱腰、拱脚的水平收敛速度变化各不相同。拱肩水平收敛在上台阶开挖时增长速度较快，在中台阶开挖后速度明显放缓。拱腰水平收敛在中台阶开挖后，收敛速度有所提升，直到下台阶开挖后才明显放缓。拱脚水平收敛速度直到仰拱开挖并施作初期支护后，才明显放缓。

综上，随着高跨比的增大，拱底隆起和围岩的水平收敛变形逐渐减小。在高跨比为1.00时，可以有效控制拱底隆起和拱肩水平收敛变形。

从数值模拟的结果来看，通过改变断面拱腰以下的形状，可以有效解决双层初期支护体系下施工过程中出现的拱肩破坏、仰拱开裂问题。

2.3.2 不同高跨比隧道支护结构受力分析

隧道开挖完成后，3种高跨比下第1层初期支护应力、第2层初期支护应力以及二次衬砌应力变化规律及特点如图14所示。由图可知，支护体系处于受压状态。

高跨比为1.00时，将隧道各位置初期支护及二次衬砌应力值的比值作为双层初期支护以及二次衬砌荷载的分担比例，结果如表6所示。由表6可知，二次衬砌在支护体系中承担的荷载较小，初期支护承担的荷载较大，二次衬砌主要作为安全储备。

1)由图14(a)可知，对于第1层初期支护，拱顶、拱肩、拱腰处所受的压力比较大，最大的压应力出现在左拱肩，为15～18 MPa，远小于混凝土的强度。相对于高跨比为0.90、0.80，在高跨比为1.00时，拱肩处的应力有所减小，分别减小了4.27%、12.12%；在拱顶、拱腰、拱脚以及拱底处应力均有较大幅度增大，但均小于混凝土的抗压强度，拱顶处的应力分别增大了4.42%、7.55%，拱腰处的应力分别增大了12.07%、22.30%，拱脚处的应力分别增大了26.94%、79.18%，拱底处的应力分别增大了27.93%、89.65%。

(a) 第1层初期支护应力

由此可知，随着高跨比的增大，第1层初期支护所承受的压力大幅度增大，但处于安全范围内。说明随着高跨比的增大，第1层初期支护更好地发挥了支护作用，对隧道的开挖更为有利。

表6 初期支护与二次衬砌荷载的分担比例(高跨比为1.00)

2)由图14(b)可知，对于第2层初期支护，拱顶、拱肩、拱腰处所受压力较大，最大的压应力出现在拱顶，约为29 MPa，接近混凝土的破坏应力。相对于高跨比0.90、0.80，在高跨比为1.00时，拱顶处的应力分别减小了8.11%、12.70%，拱肩处的应力分别减小了2.94%、7.18%，拱腰处的应力分别增大了7.66%、15.11%，拱脚处的应力分别增大了10.24%、13.90%，拱底处的应力分别增大了7.58%、30.99%，且均处于安全范围内。

由此可知，在处于接近破坏的部位如拱顶、拱肩处，随着高跨比的增大，应力逐渐减小，减小了支护破坏的可能；而在其他部位，随着高跨比的增大，应力逐渐增大，但远小于混凝土的强度。说明随着高跨比的增大，第2层初期支护更好地发挥了支护作用，对隧道的开挖更为有利。

3)对于二次衬砌，在高跨比为1.00时，相对于高跨比0.90、0.80时拱顶处的应力分别增大了2.63%、3.72%，拱肩处的应力分别减小了3.84%、5.48%，拱腰处的应力分别减小了1.33%、5.00%，拱脚处的应力分别减小了14.27%、17.73%，拱底处的应力分别减小了5.57%、11.80%。

由此可知，随着高跨比的增大，拱底二次衬砌受力逐渐减小，降低了仰拱开裂发生的可能性，而其他部位受力逐渐增大，更好地发挥了二次衬砌的支护作用。

综上，由受力可知，随着高跨比的增大，支护体系在整体上发挥了更好的支护作用，对隧道开挖更有利。对于第1层初期支护，其所承受的应力大幅度增大，但处于安全范围内；对于第2层初期支护，在处于接近破坏的部位如拱顶、拱肩处应力减小，降低了支护破坏的可能，而其他部位应力增大，但远小于混凝土的强度；对于二次衬砌，拱底应力减小，减小了拱底二次衬砌的受力。

3 高地应力软岩大变形隧道双层初期支护支护时机研究

3.1 支护时机工况设计

通过数值模拟研究隧道第2层初期支护支护时机时，仍然依据2.2节建立的隧道模型。在第1层初期支护封闭后，首先设计无第2层初期支护以及后续开挖支护工况，监测距隧道洞口0 m处的位移值，监测点布置如图12所示。提取各监测点位移值绘制隧道拱顶沉降、拱肩水平收敛、拱腰水平收敛随开挖步的变化曲线，结果如图15所示。

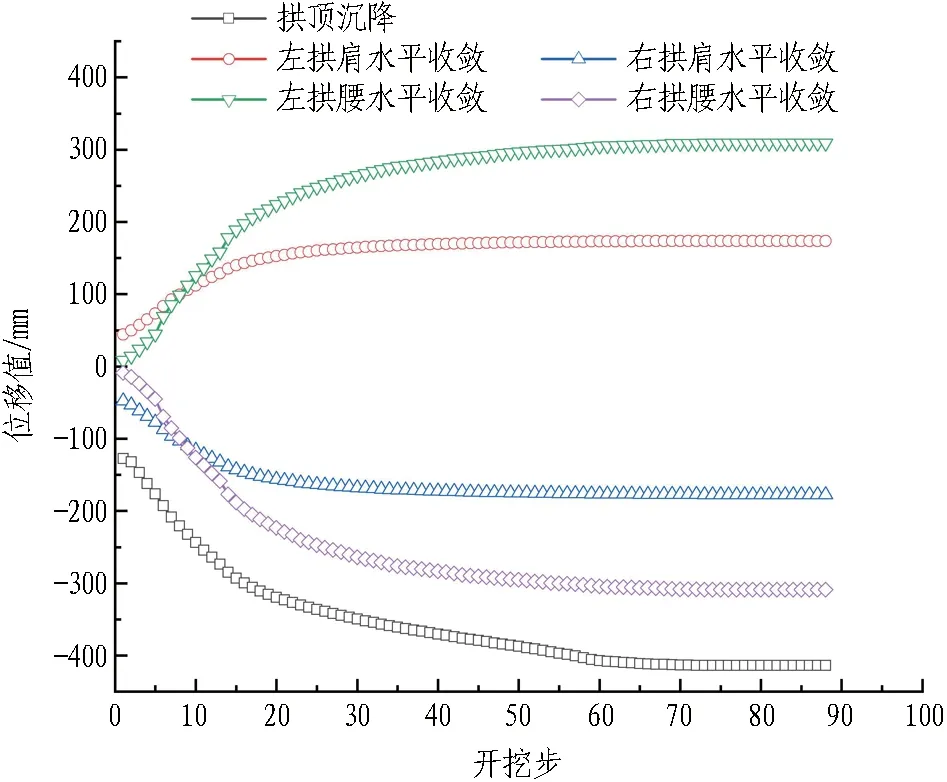
图15 监测点位移图

由图15可知，拱顶沉降始终是隧道洞周位移中的最大值，因此将控制拱顶沉降作为控制隧道变形的关键。提取该工况下的拱顶沉降数据，绘制位移随开挖步的变化曲线，结果如图16所示。其中，第14步为下台阶开挖，在此之后进行第2层初期支护。为探究第2层初期支护合理支护时机，选取第1层初期支护拱顶沉降达到300 mm(下台阶开挖2 m)、350 mm(下台阶开挖16 m)及400 mm(下台阶开挖43 m)时施作第2层初期支护作为工况(见表7)开展数值模拟。

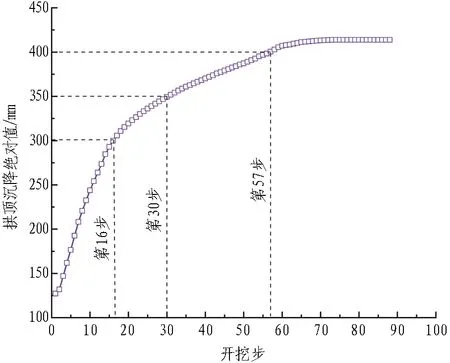
图16 拱顶沉降值

表7 第2层初期支护支护时机计算工况表

3.2 计算结果分析

3.2.1 第2层初期支护不同支护时机围岩变形分析

由于拱顶沉降是洞周位移中的最大值，因此绘制不同第2层初期支护支护时机下拱顶沉降位移图，结果如图17所示。拱顶最终沉降对比如表8所示。

图17 不同第2层初期支护支护时机下拱顶沉降值

表8 不同第2层初期支护支护时机下拱顶最终沉降对比

在第1层初期支护变形达350 mm时施作第2层初期支护与第1层初期支护变形达300 mm时施作相比，拱顶沉降最终值增大了8.97%。第1层初期支护变形达400 mm时施作第2层初期支护与第1层初期支护变形达300、350 mm时施作相比，拱顶沉降最终值分别增大了15.16%、5.68%。经分析可知，拱顶沉降最终值随第2层初期支护支护时间的推迟而增大，且增幅逐渐减小。由于支护时间推迟使得围岩未得到支护，因此变形累积增长，但因围岩内部平衡了一部分应力，使得位移增长幅度减小。

3.2.2 第2层初期支护不同支护时机下的支护结构受力分析

工况1—3开挖模拟计算完成后，取隧道进口截面作为分析截面(y=0 m处)，则不同工况下拱顶处初期支护最小主应力数值如表9所示。

表9 拱顶处初期支护最小主应力数值

经分析可知，在第1层初期支护变形达400 mm时施作第2层初期支护与第1层初期支护变形达300、350 mm时施作相比，第1层初期支护最小主应力分别减小了54.99%、40.55%，第2层初期支护最小主应力分别减小了60.91%、49.70%。

由此可知，随着第2层初期支护支护时间的推迟，双层初期支护的最小主应力显著减小。这是由于第2层初期支护支护过早时，围岩应力释放不充分，围岩未充分发挥自承能力，第2层初期支护承受过大的应力，可能会导致支护破坏，影响工程性能；而较晚施作第2层初期支护，可以使围岩应力得到充分释放，第1层初期支护能较好发挥其力学性能，第2层初期支护不至于承受过大应力，从而工程整体性能较好，降低了支护破坏发生的可能性。

综上分析可知，第1层初期支护变形达400 mm时施作第2层初期支护与第1层初期支护变形达350 mm时施作相比，拱顶沉降最终值虽增大了5.68%，但第1层初期支护应力下降了40.55%，第2层初期支护应力下降了49.70%，可见应力下降幅度远大于拱顶沉降的增大幅度。因此，在第1层初期支护变形达400 mm时，施作第2层初期支护效果较好，施工中可根据第1层初期支护设计规定的预留变形量来确定第2层初期支护的支护时机。

4 结论与建议

通过对高地应力软岩大变形隧道洞型及双层初期支护支护时机的研究，得到以下结论：

1)对于高地应力软岩隧道，采用双层初期支护代替单层初期支护后，围岩变形和变形速率虽有一定程度的减小，但在隧道施工过程中仍然出现了拱肩破坏、仰拱开裂等现象。

2)在双层初期支护条件下，对于高地应力Ⅲ级大变形围岩2车道隧道，随着隧道高跨比的增大，高地应力软岩隧道之前发生破坏的拱肩、拱底处变形减小；第1层初期支护所承受的应力增大，但处于安全范围内；第2层初期支护、二次衬砌应力减小。由此可知，对于高地应力隧道，增大隧道高跨比可有效控制围岩大变形，能使支护体系更好地发挥支护作用，对隧道的开挖更为有利。因此，建议隧道高跨比取为1.00。

3)对于高地应力Ⅲ级大变形围岩2车道隧道，适当增大第1层初期支护的预留变形量，推迟第2层初期支护的支护时间，支护应力大幅降低，因此，建议第1层初期支护变形达400 mm时施作第2层初期支护。

本文重点针对高地应力软岩大变形隧道洞型、双层初期支护施作时机开展了大变形控制研究，但大变形处治是一个系统工程，本文研究内容有限，之后将对超前小导管、仰拱管桩类型和分布、主动锚固技术等开展研究。