露天矿高陡边坡软岩蠕变-大变形试验及本构模型

缪海宾

（1.中煤科工集团沈阳研究院有限公司，辽宁 抚顺 113122；2.煤矿安全技术国家重点实验室，辽宁 抚顺 113122）

2013年初，抚顺西露天矿南帮整体边坡发生大变形，矿坑底部底鼓现象愈发突显，坡体上部地表裂缝总长度超过了2.7km，变形体前缘与后缘之间的距离达到1.5km，整个南帮大变形体面积约2.9 km2，初步估算滑体体积超过1亿m3，变形体南北向最大水平变形量达150m，垂直向最大变形量达80 m，监测数据显示其日变形量在13mm/d以上，最大时达到近200mm/d，变形体整体突显出了蠕变-大变形特性[1-3]。

软岩赋存于高陡露天边坡弱层环境下，其强度不足以承受露天矿坑底开挖引起的应力集中而产生塑性剪切滑移，开挖应力释放及调整后围岩将形成峰前弹性区、峰后塑性软化区和残余流动塑性区，随着时间不断增加，处于峰前弹性状态的围岩将由黏弹性变形向黏塑性变形转化，并伴随黏塑性应变软化现象，致使峰前弹性区围岩发生非线性蠕变-大变形现象，不仅如此，明显的非线性黏塑性流变特性也在高陡露天边坡弱层软岩峰后塑性区表现出来，其结果使得围岩变形程度增大、变形释放时间延长，大大地制约了治理工程的建设工期，进而严重影响露天矿的安全生产和经济效益。因此，在研究高陡露天边坡弱层软岩蠕变大变形特性的基础上，提出软岩蠕变大变形本构模型，揭示高陡露天边坡弱层软岩大变形非线性蠕变规律，探寻高陡露天矿边坡软岩蠕变-大变形问题的实用理论是露天开采工程中亟需开展的基础性工作[4-11]。

1 实验方案

实验主要设备为英国GDS高精度软岩流变仪，该仪器设备可进行常规单轴、三轴压缩和蠕变等实验。该实验系统主要包含250kN电机驱动数字荷载架、32MPa压力/体积控制系统、局部应变传感器、以及多功能测试模块，可开展软岩排水或不排水三轴压缩实验（UU或CU法）、单轴压缩及流变实验和三轴压缩流变实验等，具有高测试精度，可以满足软岩单轴及三轴流变大变形实验的要求。试样上安装有3个位移传感器，其中2个测定局部轴向位移，另1个测定径向位移。

通过设定不同的轴压σ1和围压σ3，分别开展常规三轴压缩试验、峰前压缩蠕变实验、峰后压缩蠕变实验。

1）通过常规三轴压缩实验，得到试样破坏全过程的σ-ε曲线，分析σ-ε曲线演化过程及特征，进而确定软岩试样的物理力学参数。

2）通过对不同围压作用下的软岩开展三轴峰前压缩蠕变实验，获取软岩蠕变曲线，研究软岩岩样轴向、径向的蠕变应变随时间的变化规律，不同围压条件下峰前蠕变试验应力施压梯度见表1。

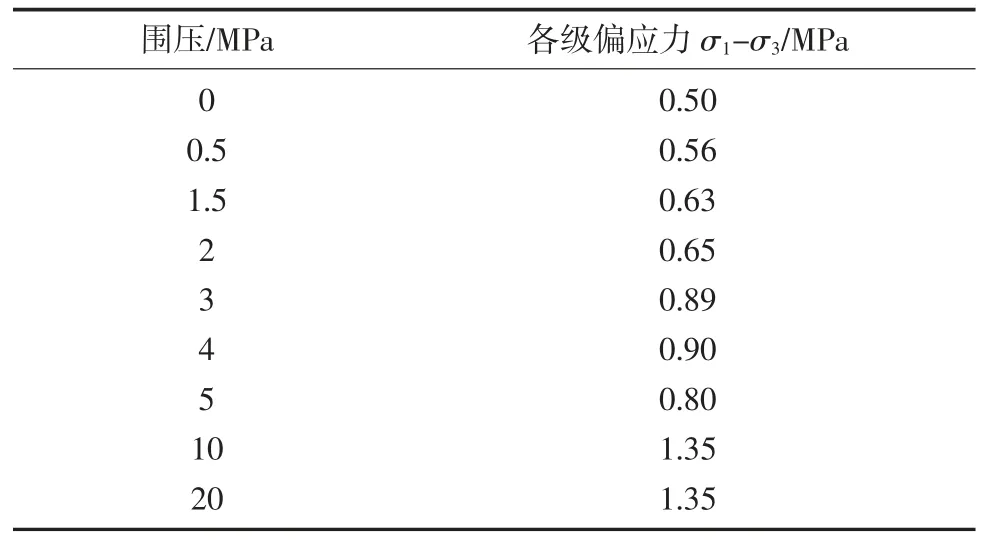
表1 不同围压条件下峰前蠕变试验应力施压梯度Table1 Stress loading gradient under different confining pressures in pre-peak creep test

3）考虑到深部软岩达到峰后塑性阶段时，围岩的变形扩展仍具有明显的时效特性。对不同围压条件下软岩峰后应变软化初段、中段及末段分别进行软岩峰后压缩蠕变实验，获得软岩试样轴向、径向的蠕变应变随时间的变化规律。采取分级加载进行峰后压缩蠕变试验，不同围压条件下峰后蠕变试验应力加载梯度见表2。

表2 不同围压条件下峰后蠕变试验应力加载梯度Table2 Stress loading gradient under different confining pressures in post-peak creep test

2 实验结果

2.1 软岩常规压缩试验结果

采用非线性最小二乘法，得到的弱层软岩三轴压缩实验全过程σ-ε曲线如图1。

图1中分别列举了围压为0、5、8、10MPa时的σ-ε曲线，经过研究σ-ε曲线的特征可知，当围压处于较低状态时，弱层软岩总体呈现为弹脆塑性特征，具有较大的强度衰减幅度，随着围压不断增大，软岩呈现出较好的延性特征，当围压达到10MPa时，软岩表现出了典型的弹塑性特征，通过对软岩的力学参数进行非线性拟合分析得到的拟合曲线如图2。由图2可知，通过实验数据拟合获得的Mohr-Coulomb强度曲线的拟合精度较高。拟合得到的软岩常规力学参数见表3。现场的实际应用中需考虑岩石剪胀因素影响，由于获得摩尔库伦强度参数的难度较低，因此对弱层软岩峰后本构模型开展了基于摩尔库伦强度准则的研究。

图1 软岩应力-应变曲线Fig.1 Stress-strain curves of soft rock

图2 软岩强度拟合曲线Fig.2 Strength fitting curves of soft rock

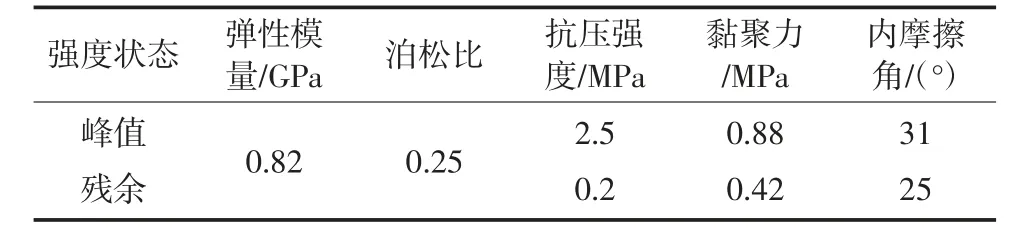
表3 软岩强度拟合参数Table3 Strength fitting parameters of soft rock

2.2 软岩峰值前压缩蠕变结果

弱层软岩峰值前蠕变曲线如图3。

通过研究图3曲线特征可知，在不断增大围压的过程中，弱层软岩的蠕应变也逐渐增大，由低围压状态下的2.5 %增大到14.5 %，彰显出弱层软岩在高应力作用下具有典型的大变形特征。

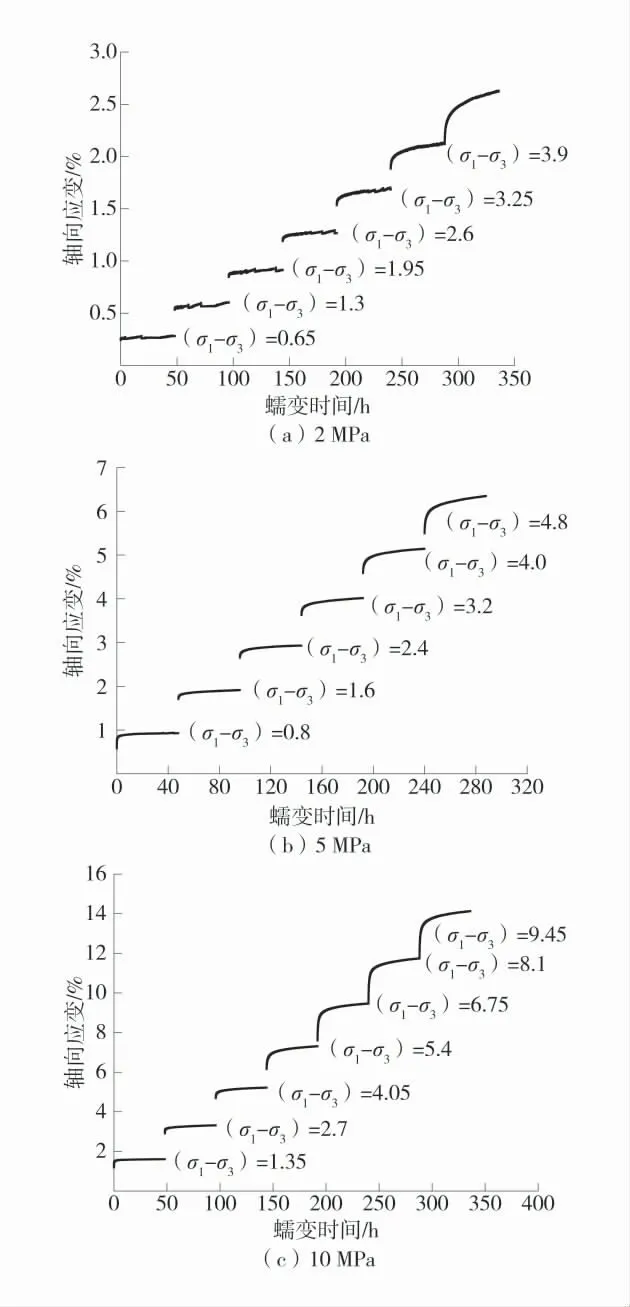
图3 不同围压条件下软岩峰前蠕变及拟合曲线Fig.3 Pre-peak creep and fitting curves of soft rock under different confining pressures

通过分析软岩的蠕变参数可得，软岩的蠕变特性与围岩的作用密不可分，具有极大相关性，围压增大，软岩的蠕应变量逐渐递增，将软岩的黏滞系数与围岩的关系进行拟合分析，得到的不同围压条件下软岩峰前蠕变参数变化规律如图4。

由图4可知，围压增大，K体（Kelvin体）与M体（Maxwell体）的黏滞系数随之却逐渐减小，其中围压对M体的影响最大，当围压达到3MPa以上，K体与M体的黏滞系数受到围岩的影响基本平稳，说明在实际工程中，应力释放较大的岩体黏滞系数要远大于围岩内部的岩体。分别对K体与M体曲线进行指数拟合研究，得到的软岩峰前蠕变K体黏滞系数η1K和M体黏滞系数η1M随围压σ3变化的指数方程为：

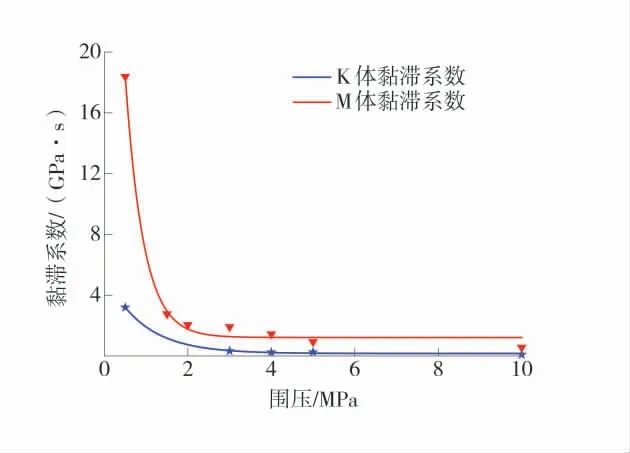
图4 不同围压条件下软岩峰前蠕变参数变化规律Fig.4 Variation law of pre-peak creep parameters of soft rock under different confining pressures

2.3 软岩峰值后压缩蠕变结果

通过峰值后蠕变实验获得的弱层软岩峰值后蠕变曲线如图5。

研究图3和图5曲线特征可得，峰值前、后的蠕变曲线特征具有较大差异，主要体现在蠕应变方面，通过观察蠕变曲线可知，软岩峰值后的蠕应变较小，在峰值后的前期和后期，其蠕应变的范围在0.1 %～0.6 %，说明软岩峰值后的蠕变特性极不稳定，这与软岩峰值后的应力路径和软岩的破裂特征有关。

图5 不同围压条件下软岩峰后蠕变及拟合曲线Fig.5 Post-peak creep and fitting curves of soft rock under different confining pressures

通过分析软岩的峰值后蠕变参数，发现同峰值前的规律类似，峰值后软岩的蠕变特性与围岩的相关性同样较大，即随着围压的增大，软岩的蠕应变量逐渐递增，将软岩的黏滞系数与围岩的关系进行拟合分析，得到的不同围压条件下软岩峰后蠕变参数变化规律如图6。

由图6可知，随着围压的增大，K体与M体的黏滞系数随之减小，围压对K体的影响最大，而M体的黏滞系数受到围岩的影响较小，说明在实际工程中，随着边坡岩体的开挖，弱层软岩会由弹性阶段向塑性阶段转化，而进入塑性软化阶段后，软岩仍然具有蠕变特性，导致弱层结构强度持续弱化的主要原因是软岩特性发生了改变。分别对K体与M体曲线进行指数拟合研究，得到的软岩峰后蠕变K体黏滞系数η2K和M体黏滞系数η2M随围压σ3变化的指数方程为：

图6 不同围压条件下软岩峰后蠕变参数变化规律Fig.6 Variation law of post-peak creep parameters of soft rock under different confining pressures

3 软岩BNSS蠕变损伤模型

通过开展软岩压缩蠕变实验并分析结果，在充分研究Burgers模型的基础上[12-16]，将非线性M-C塑性元件引入其中，并实现Burgers模型与非线性摩尔库伦的应变软化S-S塑性元件的串联，建立了BNSS蠕变损伤模型，软岩BNSS模型如图7。

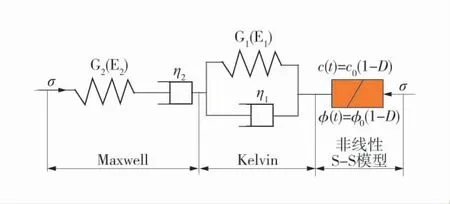
图7 软岩BNSS模型Fig.7 BNSS model of soft rock

衰减蠕变和稳定蠕变可以合理的在Burgers蠕变模型能描述出来，其σ-ε偏量本构关系为：

式中：EK为K体弹性模量；EM为M体弹性模量；ηK为K体黏滞系数；ηM为M体黏滞系数；eij为偏应变率；Sij为偏应力张量。

在σ1和σ3作用下，推导出基于Burgers模型的岩石轴向蠕变应变ε（t）为：

式中：GK为K体剪切模量；GM为K体剪切模量；K为体积模量；t为时间。

式中：v为泊松比。

将S-S塑性非线性元件引入其中，假定其服从摩尔库伦准则，即屈服函数f=0，则剪切屈服fs和拉伸屈服ft在主轴应力空间的公式分别为：

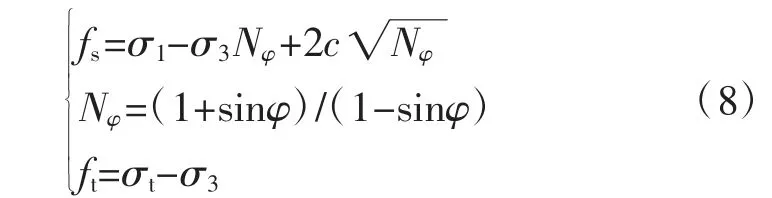
式中：φ为岩石的内摩擦角；c为岩石的黏聚力；σt为抗拉强度；σ1、σ3分别为最大、最小主应力（拉为正）。

假设c0、φ0分别为岩石初始黏聚力和内摩擦角，在蠕变过程中，c0、φ0的蠕变损伤方程应为：

式中：D为损伤变量；t为时间。

将式（9）代入式（8），得到应变软化S-S塑性非线性元件与时间有关的剪切屈服fs准则为：

BNSS蠕变损伤模型中总偏应变率eij为：

式中：eijK为K体偏应变；eijM为M体偏应变；eijP为黏塑性偏应变。

对Kelvin体，有：

对Maxwell体，有：

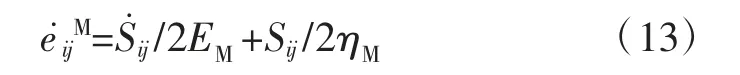
应变软化S-S非线性体的偏应变率为：

式中：g为势函数；evolP为黏塑性体应变；λ为仅在塑性流动阶段非零的参数，通过fs=0确定；σij为应力分量；δij为应力张量；σ1、σ2、σ3分别为最大主应力、中间主应力和最小主应力。

势函数g形式如下：

式 中：Nψ为 塑 性 势 函 数，Nψ=（1+sinΨ）/（1-sinΨ）；Ψ为岩石剪胀角。

4 结 语

1）通过软岩三轴压缩蠕变实验，得到的其常规应力-应变曲线表现出了明显的弹脆塑性向弹塑性转化的趋势，且该现象较为明显。通过拟合得到软岩峰值前及峰值后残余强度指标黏聚力和内摩擦角。

2）通过分析软岩的蠕变曲线规律，软岩的蠕应变对围压的敏感度较高，在低围压、高应力作用下具有典型的大变形特征；其峰值后的蠕变特性不稳定，易受外界因素的干扰。

3）软岩峰值前的黏滞系数受围压的影响大，随着围压的增大，K体与M体的黏滞系数逐渐减小，围压达到3MPa后二者趋于平稳；围压对峰值后的黏滞系数影响较小，但对K体黏滞系数影响的要较M体的大，弱层软岩会由弹性阶段向塑性阶段转化。

4）通过实验获得的软岩蠕变-大变形试验规律及建立的本构模型，可为后期蠕变-大变形高陡边坡破坏机理及防治措施的研究提供实验依据及理论支撑。