土压平衡盾构楔犁刀松动砂卵石地层力学行为研究
张晋勋, 殷明伦, *, 江玉生, 江 华, 周刘刚, 孙正阳,
(1. 北京城建集团有限责任公司, 北京 100088; 2. 中国矿业大学(北京)力学与建筑工程学院, 北京 100083)
0 引言
在城市地铁建设过程中,盾构因具有开挖速度快、安全性高、对地面交通影响小等优势被普遍应用。砂卵石地层在北京、沈阳、兰州、成都等地区分布较广,盾构在砂卵石地层中掘进,刀具磨损十分严重,而刀具的寿命直接决定着施工工期和工程造价。因此,研究盾构刀具与砂卵石地层的相互作用尤为重要。
对于刀具与土体相互作用的研究最早集中在农业中耕具与土体相互作用的受力计算方面,国外学者通过理论分析建立了较多刀具受力计算的理论模型[1-6]。Rowe等[7]针对斜刃耕具切削土壤时刀具的受力进行了分析,建立了二维刀具受力模型,并分析了不同切削速度、不同土体性质对刀具受力的影响。Mckyes等[8]、Godwin等[9]分别建立了刀具切削土体三维受力模型及土体破坏模型。由于盾构刀具切削土体与耕具的作用模式有一定的相似性,国内外学者在对盾构切刀进行受力分析时借鉴了耕具的相关描述,建立了切刀切削地层力学模型,并进行了试验、仿真验证[10-17]。也有部分学者在盾构总扭矩计算过程中,分析了每把刀具在切削过程中的受力状态,但计算过程较为简单,未考虑刀具类型、配置等因素的影响[18]。
地层条件不同时,刀土相互作用机制存在较大差异,例如: 盾构在软土地层或砂层中掘进时,刮刀作为主切削刀切削地层,先行刀起保护、导流等作用,辅助刮刀切削地层; 而盾构在砂卵石地层中掘进时,在刀盘转动力矩的作用下,刀具刃部楔入砂卵石地层并沿环向运动轨迹对开挖面进行楔犁作用,在环向与轴向压应力作用下,原状砂卵石颗粒咬合结构被破坏,卵石本身不破碎,但颗粒骨架作用消失、内摩擦力减小,密实颗粒体被松动成为散体颗粒,并在自身重力和刮刀辅助作用下从开挖面剥落,经刀盘开口进入土舱,完成楔犁松动的过程。由于砂卵石地层与软土地层刀土相互作用机制截然不同,因此,将松动砂卵石地层的刀具命名为“楔犁刀”,与应用于软土地层起切削作用的刀具相比,此类型刀具刀体超高(可达220 mm),合金块高强耐磨耐冲击。
现有针对刀具与砂卵石地层相互作用的研究较少,例如: 张晋勋等[19]研究了富含大粒径漂石的砂卵石地层重型刀具破岩问题,研究对象是大粒径漂石,刀石相互作用机制与中小粒径砂卵石地层不同; 黄清飞[20]以多个砂卵石地层盾构工程为例,提出了砂卵石地层中先行刀切削地层与刮刀剥落渣土的刀具切削机制; 彭均等[21-22]针对先行刀切削地层进行了离散元数值计算分析,但未给出计算模型,且未对刀具梯次布置等进行深入研究。
为了解砂卵石地层中土压平衡盾构楔犁刀与刮刀组合作用于岩土体的力学行为,本文分析了楔犁刀楔犁松动砂卵石地层时刀具的受力状态、楔犁刀楔犁松动及刮刀剥落组合受力状态,揭示楔犁刀与砂卵石地层的相互作用,以期为砂卵石地层盾构设计提供理论基础。
1 楔犁刀楔犁松动砂卵石地层单刀受力分析
1.1 楔犁刀运动分析及坐标系建立
楔犁刀是土压平衡盾构在砂卵石地层中掘进的专用刀具,具有高耐磨、耐冲击的特征,刀具初装图如图1所示。

图1 楔犁刀初装图
刀盘前方原状砂卵石及渣土均受土压作用,力可以连续传递,地层可以等效为连续体进行计算分析。为研究楔犁刀的受力状态,首先对其运动轨迹进行分析。在盾构掘进过程中,楔犁刀的运动由沿着盾构掘进方向的直线运动、垂直于隧道轴线方向的转动2部分组成。为方便分析,将楔犁刀简化为一个点,并建立圆柱坐标系。其三维螺线形运动轨迹如图2所示,运动方程如式(1)所示。坐标系中,Z方向为盾构掘进方向,W方向为刀盘半径方向,Θ方向为转动方向。

图2 楔犁刀螺线形运动轨迹
(1)
式中:v为盾构掘进速度;t为时间;Ri为楔犁刀轨迹半径;ω为刀盘转速。
为了便于进行受力分析,以单把楔犁刀为对象,建立局部直角坐标系,如图3所示。图中,x方向为刀具转动方向,即刀盘的环向方向;y方向为刀具的顶进方向,即盾构掘进方向。下文楔犁刀的受力分析均采用该局部直角坐标系。
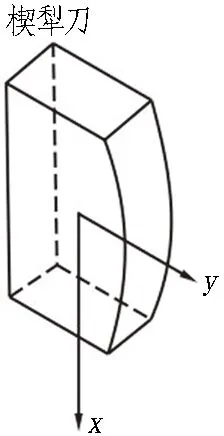
图3 楔犁刀局部直角坐标系
1.2 楔犁松动作用下砂卵石土破坏强度计算
楔犁刀在楔犁松动地层时受刀刃楔犁原状地层反力F1、刀身楔犁原状地层反力F2、刀身楔犁松动土反力F3、刀侧侧向土压力F4共同作用。其中,F1可分解为作用在刀刃的法向力F11及切向摩阻力F12; 楔犁刀正反两侧均受F4作用,故仅需考虑抵抗F4产生的侧摩阻力F41。楔犁刀楔犁松动地层时的受力示意如图4所示。
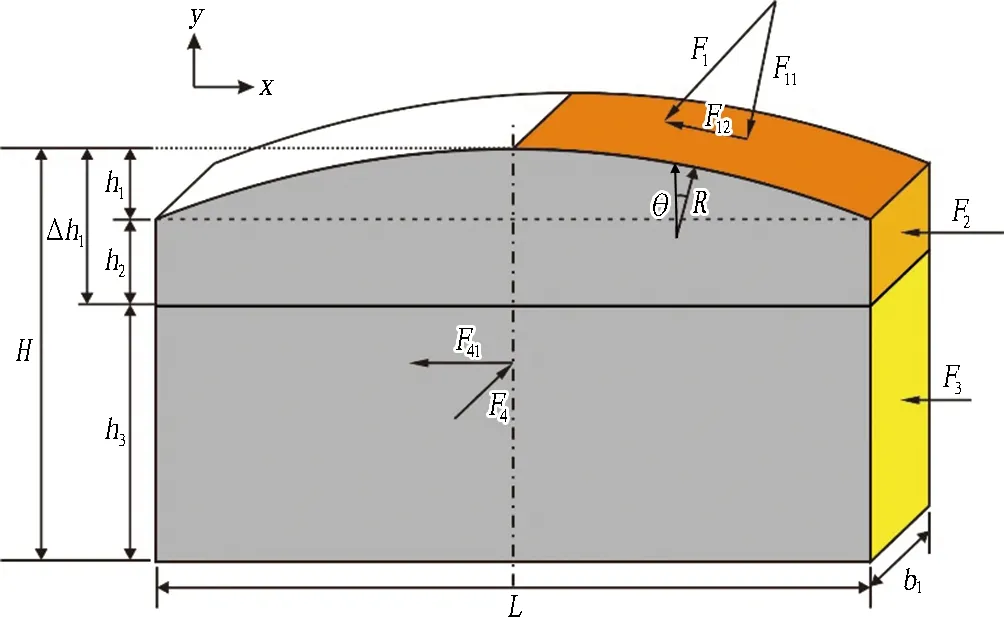
H为楔犁刀楔犁地层深度; Δh1为原状地层切深; h1为刀刃贯入原状地层深度; h2为刀身贯入原状地层深度; h3为松散渣土切深; b1为楔犁刀有效厚度; L为楔犁刀宽度; R为楔犁刀弧形刀刃半径; θ为楔犁刀迎土面一点与y方向的夹角。
在研究楔犁刀对地层的楔犁松动作用时,应分别研究楔犁刀刀刃与楔犁刀刀身的楔犁作用。
1.2.1 楔犁刀刀刃楔犁作用下原状地层破坏强度计算
楔犁刀刀刃划过区域砂卵石土的破坏机制与地基土整体剪切破坏相近,其力学行为表现为: 楔犁刀在荷载作用下沿规定方向楔犁砂卵石地层时,刀刃迎土面形成一个刚性核,刚性核挤压两侧土体,使得被开挖土体的应力超过土体强度,密实原状地层中砂卵石颗粒间的咬合作用被破坏,成为松散结构,沿滑移面向刀身两侧运动,示意如图5所示。由于掌子面与重力方向平行,计算地层破坏强度时不考虑土体自重,计算时可采用Terzaghi地基承载力计算公式进行计算。
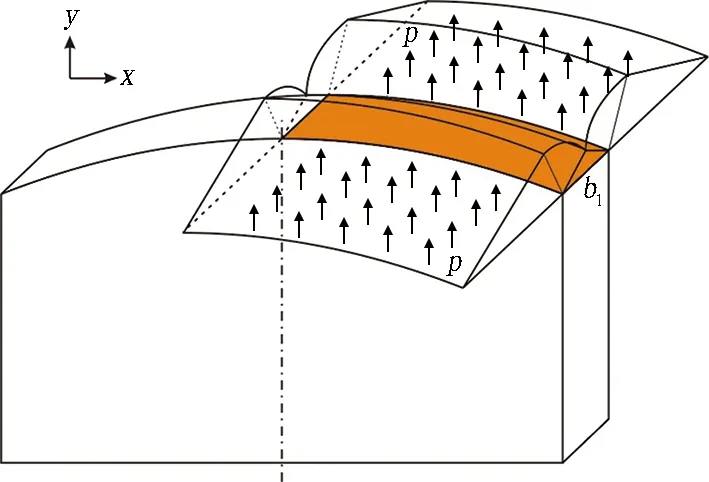
p为土压力。
根据Terzaghi解,楔犁作用下砂卵石土破坏强度
pu1=pN1+cN2。
(2)
式中:c为原状地层黏聚力;N1与N2可依据prandtl解取值,2参数取值仅取决于砂卵石土的内摩擦角φ,计算公式为
(3)
N2=cotφ·(N1-1)。
(4)
土压力p由盾构中心深度H0、刀具在刀盘上的位置所决定。设λ为侧压力系数,γ为地层重度,盾构中心处静止土压力p0=λγH0,故土压力p可按式(5)计算。
p=p0+λγRi(α+π)=λγ[H0+Ricos(α+π)]。
(5)
式中α为刀具旋转角度。
楔犁刀所处位置土压力计算模型如图6所示。

R0为盾构开挖半径。
1.2.2 楔犁刀刀身楔犁作用下原状地层破坏强度计算
众多学者研究了刀具及土体的相互作用机制,基于楔犁刀的作用机制,刀身楔犁作用下地层破坏强度可采用Mckyes-Ali模型[8]进行计算,楔犁刀作用时地层的失效区分为中心失效区与侧面2个半月形失效区,其潜在破坏面如图7所示。

图7 楔犁刀刀身楔犁砂卵石地层潜在破坏面示意图
刀身在楔犁地层过程中的受力状态分析,以楔犁刀刀身楔犁密实原状地层部分为例,计算模型如图8所示。刀身楔犁原状地层部分所受合力F2计算公式见式(6)。

p为刀具所在位置的土压力; δ1为刀具楔犁角度,楔犁刀刀身楔犁角度δ1=90°; β1为失效面破坏角,依据朗肯被动土压理论,为半月形失效区角度,根据几何关系,ρ1=90°; r1为半月形失效区半径,r1=h2cot β1。
(6)
式中:F21为刀身对中心失效区土体的作用力;F22为刀身对两侧半月形失效区土体的作用力;Nγ1,Nc1,Np1计算公式分别为
式中ψ为刀具与地层间的摩擦角。
为了便于分析,假设松动原状地层(或松散渣土)刀身不同位置的力均匀分布。
因此,刀身楔犁作用下地层破坏强度可由式(7)计算。
(7)
1.2.3 楔犁指数及松散渣土破坏强度计算
楔犁刀松动土层并不是一次楔犁完成,而是反复作用,随着楔犁刀划过土层次数的增加,原状地层中砂卵石间的咬合作用逐渐被破坏,最终结构被彻底松动而成为一种强度不变的摩擦流体,其强度为砂卵石土的残余强度。通过直剪试验获取残余强度破坏包线,得到其残余黏聚力cr,残余内摩擦角φr,进而求得松散地层的残余强度pr。

(8)
楔犁刀松动土层的效果取决于土层的力学特性、渣土改良效果及土压力,与楔犁次数正相关。因此,定义楔犁指数
(9)
式中η为楔犁常数,当地层中黏土矿物含量高、渣土改良效果差、土压力大时,松动效果差,楔犁常数小。
n次楔犁后刀刃楔犁作用下松散渣土的破坏强度
(10)
n次楔犁后刀身楔犁作用下松散渣土的破坏强度
(11)
式(10)—(11)中pr1、pr2分别为刀刃、刀身楔犁作用下地层的残余强度。
依据式(10)及式(11)可在已知原状地层破坏强度、残余强度、楔犁指数的情况下计算松散渣土的破坏强度。
1.3 楔犁刀楔犁砂卵石地层刀具受力分析
将楔犁刀楔犁砂卵石地层时所受的各部分力沿x(环向)、y(轴向)方向分解,可得: 1)楔犁刀刀刃挤压原状地层荷载p11、p12产生的土抗力在x方向上的分量Fx1; 2)楔犁刀刀刃挤压原状地层荷载p11、p12产生的土抗力在y方向上的分量Fy1; 3)楔犁刀刀身楔犁原状地层荷载p2产生的土抗力Fx2; 4)楔犁刀刀身楔犁松散渣土荷载p3产生的土抗力Fx3; 5)楔犁刀的侧面摩擦阻力Fx4。

以单层楔犁刀楔犁松动原状地层为例计算刀具受力,计算模型及受力分解分别如图9和图10所示。

图9 楔犁刀楔犁松动砂卵石地层受力计算模型

(a) 楔犁刀楔犁地层整体受力分解
单层楔犁刀楔犁松动原状地层的环向阻力Fx由4部分组成: 楔犁刀刀刃挤压原状地层荷载p11、p12产生的土抗力在x方向上的分量Fx1,楔犁刀刀身楔犁原状地层荷载p2产生的土抗力Fx2,楔犁刀刀身楔犁松散渣土荷载p3产生的土抗力Fx3以及楔犁刀的侧面摩擦阻力Fx4。楔犁刀松动原状地层轴向阻力Fy主要为刀刃挤压原状地层荷载p11、p12产生的土抗力在y方向上的分量Fy1。
(12)
各部分力计算方法如式(13)—(19)所示。式中:μ为刀土摩擦因数,μ=tanψ;p11=pu1cosψ。
1)刀刃挤压原状地层环向阻力
(13)
2)刀刃挤压原状地层轴向阻力
(14)
3)刀身楔犁原状地层环向阻力
Fx2=p2h2b1=pu2h2b1。
(15)
4)刀身楔犁松散渣土环向阻力
(16)
5)刀侧环向摩擦阻力
Fx4=μp4LH=λpL(h1+h2+h3)tanψ。
(17)
6)刀刃挤压松散渣土环向阻力
(18)
7)刀刃挤压松散渣土轴向阻力
(19)
基于式(13)—(19)计算得到楔犁地层时楔犁刀不同部位所受的阻力,可根据刀具的不同工作状态计算得到单刀楔犁地层所需的环向松动力Fx和轴向顶进力Fy,进而可计算盾构掘进时整盘刀具楔犁松动地层所需的贯入推力F及扭矩T。
1.4 楔犁刀楔犁砂卵石地层受力计算实例
采用该计算方法对北京新机场线磁各庄—1#风井区间工程楔犁刀楔犁松动砂卵石地层进行计算分析。砂卵石地层物理力学参数如表1所示。

表1 砂卵石地层物理力学参数
楔犁刀设计图如图11所示,刀具结构尺寸及掘进参数如表2所示。

图11 楔犁刀设计图(单位: mm)

表2 楔犁刀尺寸及掘进参数
采用本文所述计算方法,可将表1和表2的数据代入式(13)—(19)中,计算得到当该把楔犁刀与盾构中心高度一致时,刀刃挤压原状地层环向阻力Fx1=6.16 kN,刀身楔犁原状地层环向阻力Fx2=1.19 kN,刀身楔犁松散渣土环向阻力Fx3=0.06 kN,刀侧环向摩擦阻力Fx4=0.26 kN,则环向阻力Fx=7.67 kN; 刀刃挤压原状地层轴向阻力Fy1=18.14 kN。
依据式(5)可求出盾构刀盘上任意一点的土压力,进而求得刀盘任意位置处楔犁刀楔犁地层所需的轴向顶进力及环向松动力。计算得刀具所处位置土压力为60~180 kPa,刀具环向松动力为4.11~11.24 kN,轴向顶进力为9.76~26.51 kN。
2 楔犁刀楔犁松动地层与刮刀剥落渣土的刀具组合受力分析
砂卵石地层盾构刀盘正面通常配备楔犁刀及刮刀2种刀具,其中,楔犁刀起主要的楔犁松动作用,刮刀剥落松动的渣土。本节主要研究楔犁刀楔犁松动地层与刮刀剥落渣土时刀具组合的整体受力情况。
2.1 刮刀剥落松散渣土受力分析
部分学者已对刮刀切削软土受力计算模型进行了较为深入的研究,并得到了系统性成果。本文采用暨智勇[13]研究得到的模型(见图12)及公式,计算刮刀剥落松散渣土时前刃面的受力P。

(a) 地层失效示意图

(20)
式中:P1为刮刀对两侧半月形楔块的作用力;P2为刮刀对中心楔块的作用力;Nγ2,Nc2,Np2计算公式分别为
由于掌子面与重力方向平行,计算刮刀剥落渣土刀具受力时不考虑土体自重,故γ=0; 砂卵石土为无黏性土,与刮刀之间无黏结力,故ca=0; 当砂卵石土被完全松动后,土的抗剪强度为其残余强度,黏聚力为0,故cr=0。因此,刮刀剥落松散渣土时前刃面的力
P=P1+2P2=pΔh3Np2b2。
(21)
(22)
2.2 单梯次楔犁刀楔犁松动地层及刮刀剥落渣土刀具受力分析
根据楔犁刀楔犁松动原状地层、刮刀剥落松散渣土的工作原理,可建立如图13所示的单梯次楔犁刀楔犁松动地层与刮刀剥落渣土组合受力计算模型。

图13 单梯次楔犁刀楔犁松动地层与刮刀剥落渣土组合受力计算模型
单梯次楔犁刀楔犁松动地层与刮刀剥落渣土组合的环向松动力Fx与轴向顶进力Fy计算公式为
(23)

2.3 两梯次楔犁刀楔犁松动地层及刮刀剥落渣土刀具受力分析
根据楔犁刀楔犁松动原状地层、刮刀剥落松散渣土的工作原理可以看出,盾构在砂卵石地层中掘进,楔犁刀承担主要作用,单次不换刀掘进距离主要取决于楔犁刀刀具寿命,而楔犁刀的刀具寿命就是合金块的工作寿命。在选取最适合砂卵石地层掘进的合金材料的前提下,合金块长度成为刀具寿命的决定性因素。为了延长盾构单次不换刀掘进距离,克服合金块焊接长度受限的难题,可采用楔犁刀两梯次布置的方法,实现第1梯次楔犁刀先磨损、第2梯次楔犁刀后磨损的“接力”磨损方式,延长单次掘进距离。
两梯次楔犁刀与刮刀组合的环向松动力Fx与轴向顶进力Fy可由式(24)计算。
(24)

随着盾构连续掘进,起主要楔犁作用的第1层楔犁刀磨损逐渐累积,为了更准确地计算整盘刀具与地层作用所需的扭矩及推力,可根据第1层楔犁刀磨损情况的不同,将刀具受力划分为2个阶段。
1)阶段1为掘进初始阶段。此阶段第1层楔犁刀A尚未发生严重磨损,其切深Δh1小于2层楔犁刀的高差H1,此时第1层楔犁刀A楔犁原状地层,而第2层楔犁刀B楔犁松散渣土,计算模型如图14所示。

图14 两梯次楔犁刀楔犁松动地层第1阶段受力模型

(25)
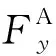
(26)
式(25)—(26)中n为楔犁次数,由于该阶段仅有楔犁刀A楔犁原状地层,因此
(27)
根据该阶段楔犁刀A与楔犁刀B的相对位置H1>Δh1,可知该阶段n>1。
2)阶段2为长距离掘进阶段。此阶段第1层楔犁刀A已发生严重磨损,第1层楔犁刀切深Δh1大于2层楔犁刀的高差H′1,此时第1层楔犁刀A与第2层楔犁刀B均楔犁松动原状地层,计算模型如图15所示。

图15 两梯次楔犁刀楔犁松动地层第2阶段受力模型
在阶段2时,两梯次楔犁刀和刮刀组合模型的环向松动力Fx计算公式中,楔犁刀A与楔犁刀B的环向松动力计算公式为
(28)
轴向顶进力Fy计算公式中的分量计算方法为
(29)
2.4 整盘刀具楔犁地层所需扭矩与贯入推力实例计算
盾构刀具与岩土体相互作用的受力分析是盾构设备选型及掘进参数设计的关键依据之一。本节根据实际工程地质概况及常规施工参数,基于2.3节所述计算方法对扭矩和贯入推力进行计算,计算参数如表3所示。

表3 计算参数
将表3中的计算参数代入计算模型中,可以计算得到: 当刀具所处位置土压力与盾构中心处土压力相同时,单把楔犁刀A楔犁砂卵石地层所需环向松动力为5.69 kN,所需轴向顶进力为18.44 kN; 单把楔犁刀B松动砂卵石地层所需环向松动力为3.68 kN,所需轴向顶进力为11.69 kN; 单把刮刀所需环向松动力为1.57 kN,所需轴向顶进力为1.03 kN。
根据单把刀具所需环向松动力及轴向顶进力,可推算得到整盘刀具松动砂卵石地层时所需的扭矩及贯入推力。以双层楔犁刀、单层刮刀布置的直径9.04 m刀盘为例,全刀盘共布置楔犁刀132把,其中,第1层楔犁刀(图14中楔犁刀A)79把,第2层楔犁刀(图14中楔犁刀B)53把,刀具布置方式如表4所示。刀盘共布置刮刀78对,刀具布置方式如表5所示。刀具梯次布置示意图如图16所示,整个刀盘刀具布置如图17所示。

表4 楔犁刀布置方式

图16 刀具梯次布置示意图(单位: mm)

图17 刀盘刀具布置图
根据刀具布置方式可以看出,刀具基本呈对称布置,在计算刀具受力时,对称的刀具所处位置的土压力的平均值即为盾构中心处的土压力p0。故可简化计算,认为每把刀具所处位置的土压力均为p0,简化后计算结果与简化前计算结果相同。则可根据式(30)和式(31)计算得到整盘刀具楔犁地层所需的扭矩T及贯入推力F。
(30)
(31)
式(30)—(31)中:i为刀具轨迹编号;Ai、Bi分别为轨迹半径为Ri的第1层、第2层楔犁刀数量;Ci为轨迹半径为ri的刮刀数量。
经计算,本工程在所述计算工况下整盘刀具楔犁地层所需扭矩及贯入推力分别为2 526.52 kN·m、2 156.18 kN。
将本文提出的刀具梯次布置松动剥落地层所需的贯入推力和扭矩计算模型代入徐前卫[23]提出的推力和扭矩计算模型中进行计算,并与实际工程中的扭矩和推力进行对比验证。推力和扭矩计算相关参数见表1、表3与表6。

表6 盾构掘进总推力及总扭矩计算参数表
盾构总推力F总主要包括盾壳与地层间的摩阻力、盾构辐条土舱隔板和面板辐条抵抗土压力而产生的正面阻力。根据表6中的参数,依据文献[23]中式(5.86)计算得到盾构总推力为42 568 kN,与实际掘进推力基本吻合。其中,盾构外壳与地层之间的摩阻力为29 786 kN,盾构推进的正面阻力为12 782 kN。由本文提出的方法计算得到刀具松动地层所需的贯入推力为2 156 kN,是盾构推进正面阻力的一部分,仅占总推力的4.8%。
盾构总扭矩T总主要包括4部分: 刀具松动土体所需的力矩T(由于中心刀半径很小,对扭矩影响不大[24],故仅考虑楔犁刀、刮刀的扭矩)、刀盘正面的摩擦力矩T2、刀盘周边的摩擦力矩T3和刀盘开口处切削渣土所需的力矩T4。将文献[23]中刀具松动土体所需力矩T1的计算方法修正为本文提出的计算方法(式(30))后,依据文献[23]中式(5.91)—(5.95)计算得到总扭矩T总为6 934 kN·m,其中,刀具松动土体所需的力矩T为2 527 kN·m(依据本文提出的方法计算得到),占总扭矩的36.4%,其余部分扭矩依据表6中参数计算得T2为1 109 kN·m,T3为2 579 kN·m,T4为719 kN·m,总扭矩约为6 934 kN·m。
选取北京新机场线磁各庄—1#风井区间工程左右双线400~1 000环实际掘进扭矩,与本文计算结果、文献[23]计算结果进行对比,如图18所示。
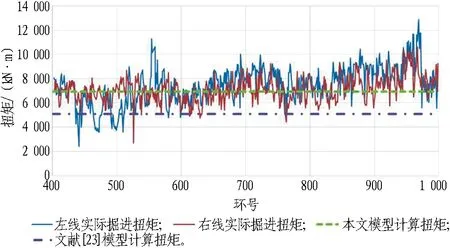
图18 实际掘进扭矩与计算结果对比
分析结果显示,与文献[23]提出的计算方法相比,采用本文提出的计算方法计算得到的总扭矩与实际掘进扭矩更为吻合,证明了模型的准确性。因此,可以采用本文提出的刀具梯次布置受力计算方法估算楔犁刀松动地层时所受的阻力。
2.5 整盘刀具楔犁地层所需扭矩及贯入推力影响因素分析
为研究参数变化对贯入推力和扭矩的影响,以表3中的计算参数作为基本工况,将不同梯次楔犁刀的高差、刮刀与楔犁刀的高差和贯入度3个参数作为变量,研究不同刀具布置方式对推力和扭矩的影响。
2.5.1 楔犁刀高差
在表3计算参数的基础上,设置0、10、20、30、35、40、50、60、70 mm共9种楔犁刀高差,研究不同梯次楔犁刀高差对刀盘松动地层所需扭矩及贯入推力的影响,计算结果如图19所示。
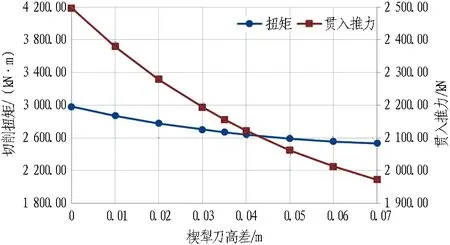
图19 不同楔犁刀高差下刀具楔犁地层所需的扭矩及贯入推力的变化曲线
随着楔犁刀高差的逐渐增大,整盘刀具楔犁地层所需的扭矩及贯入推力均呈现出减小的趋势,贯入推力显著减小,扭矩减小趋势较为缓慢,说明楔犁刀的分层布置可以有效减小扭矩及贯入推力。
2.5.2 楔犁刀与刮刀高差
在表3计算参数的基础上,设置30、40、50、60、70、80、90、100、110 mm共9种楔犁刀与刮刀的高差,研究楔犁刀与刮刀的高差对刀盘楔犁地层所需扭矩及贯入推力的影响,计算结果如图20所示。

图20 不同楔犁刀与刮刀高差下刀具楔犁地层所需的扭矩及贯入推力的变化曲线
随着楔犁刀与刮刀高差的逐渐增大,刀盘扭矩先减小后略微增大,当楔犁刀与刮刀高差为0.09 m时扭矩最小; 贯入推力缓慢减小。计算结果表明: 楔犁刀与刮刀高差变化对扭矩及贯入推力总体影响较小; 楔犁刀超前刮刀布置可以减小刀具的扭矩和贯入推力,此种刀具布置方式对刀具起到一定的保护作用,当高差大于0.07 m后,增加高差对贯入推力和扭矩无明显影响。
2.5.3 贯入度
切深为贯入度除以同一轨迹上的刀具数量,由于盾构刀盘靠近中心部分刀具数量较少,而外周刀具数量较多,因此在相同贯入度条件下,不同位置刀具的切深不同。
在表3计算参数的基础上,设置30、36、42、48、54、60、66、72、78、84、90 mm共11种贯入度,研究贯入度对刀盘松动地层所需扭矩及贯入推力的影响,计算结果如图21所示。

图21 不同贯入度下刀具楔犁地层所需的扭矩及贯入推力的变化曲线
随着刀具贯入度的逐渐增大,刀盘扭矩显著增大,所需贯入推力也明显增大,但增加趋势有所减缓。
推进速度为贯入度与刀盘转速的乘积,工程中要保证较高的掘进速度,需综合考虑这2个因素。由于砂卵石地层中刀盘转速过大会导致刀具断齿等冲击破坏现象发生,因此,应采用高的贯入度实现快速高效掘进。应在设备选型时增加贯入推力及扭矩储备,避免出现盾构卡死等情况。
3 结论与讨论
为了分析砂卵石地层土压平衡盾构楔犁刀与刮刀组合松动剥落岩土体时刀具的受力情况,求解了楔犁刀楔犁作用下砂卵石土的破坏强度,阐明了楔犁刀楔犁松动的开挖机制,提出了楔犁指数的概念及其计算公式,分析了楔犁刀楔犁松动砂卵石地层时刀具的受力,进而提出了砂卵石地层盾构楔犁刀梯次楔犁松动地层与刮刀剥落渣土的受力计算方法,得到整盘刀具松动地层所需的扭矩及贯入推力。研究结果表明:
1)刀盘前方原状砂卵石及渣土均受土压作用,土压力可以连续传递,地层可以等效为连续体进行计算分析,采用Terzaghi地基承载力模型与Mckyes-Ali模型可以计算刀具楔犁作用下砂卵石地层的破坏强度。
2)区别于以往刀具切削地层的受力分析,本文引入楔犁指数k表征了楔犁刀反复松动地层、地层颗粒间咬合作用被逐渐破坏、地层强度逐渐降低的楔犁松动机制,可计算复杂刀具配置条件下整盘刀具楔犁地层时的受力情况。
3)依据楔犁刀楔犁松动砂卵石地层的刀具受力分析结果,可计算单把楔犁刀楔犁地层所需的环向松动力及轴向顶进力,进而依据楔犁刀梯次楔犁松动地层与刮刀剥落渣土的受力计算方法,计算得到整盘刀具楔犁地层所需的扭矩及贯入推力,计算结果与实际工程中盾构掘进参数相近,验证了计算模型的准确性。
4)本文提出的刀具梯次楔犁松动剥落地层受力分析方法可为刀具布置设计提供理论依据。由不同刀具布置方式下整盘刀具楔犁地层所需贯入推力和扭矩的计算分析可知,楔犁刀分层、超前于刮刀布置可以有效降低刀具松动地层所需的贯入推力和扭矩,进而达到降低盾构掘进所需的总推力及总扭矩。
楔犁刀与贝壳刀和先行刀在作用机制、尺寸、适用性等方面明显不同。楔犁刀楔犁松动原状砂卵石地层,破坏颗粒咬合结构,而不破碎卵石颗粒本身,这种对砂卵石地层的松动作用与传统的贝壳刀或先行刀切削细颗粒土层是不同的,“楔犁”一词可以更准确地反映整个作用过程,因此将这种刀具定义为楔犁刀。楔犁刀具设计也应按楔犁刀松动地层的作用机制进行,与常规贝壳刀或先行刀不同。另外,将砂卵石地层等效为连续介质,提出了复杂刀具配置条件下刀具楔犁松动开挖地层所需贯入推力和扭矩的计算方法,解决了盾构总推力和总扭矩计算模型在复杂刀具配置条件下的适用性问题。


