环境规制、绿色技术创新与经济高质量发展的影响研究

王斌会 伍桑妮暨南大学管理学院广州5063 暨南大学经济学院广州 5063

随着改革开放和现代化进程加快，我国经济水平不断提高，但我国长期实行的粗放式经济发展，对环境造成了不可逆转的危害，对人们身体健康也产生了一定影响。“高质量发展”表述的提出，表明我国经济已从高速增长阶段转向高质量发展阶段。而高质量发展根本在于经济的活力、创新力和竞争力，经济发展的活力、创新力和竞争力都与绿色发展密不可分。环境规制和绿色技术创新作为绿色发展的重要手段，对我国经济高质量发展起着至关重要的作用。因此，厘清环境规制、绿色技术创新与经济高质量发展之间的关系，把握环境规制强度和绿色技术创新之间的协调关系；科学合理地制定环境规制力度，在不污染环境的前提下，最大限度的实现社会经济发展、促进企业的绿色技术创新能力，对我国未来生态环境保护和经济发展方向有着重要的指导意义。

1 文献回顾

现阶段关于环境规制和绿色技术创新的研究主要从它们之间的相关关系和异质性环境规制对绿色技术创新产生影响的差异性这两方面展开。环境规制和绿色技术创新之间的相关关系取决于“补偿效应”和“成本效应”的相互作用。“补偿效应”是指环境规制政策的实施会倒逼企业进行绿色技术创新，规制企业的工业排放，提高污染排放处理标准，从而提高企业的绿色技术创新效率；“成本效应”是指环境规制政策的实施会挤占企业部分技术创新成本，使得企业技术创新投入减少，降低企业绿色技术创新效率。肖黎明等［1］根据研究得出环境规制与绿色技术创新效率之间存在“U”型关系的结论。刘章生等［2］以环境规制为门槛变量建立了门槛模型，得到了环境规制与绿色创新能力之间存在倒“U”型关系的结论。高萍和王小红［3］研究了在绿色技术创新效率不同的地区，环境规制强度对绿色技术创新效率影响的差异性。Shang等［4］研究结果认为环境规制会对绿色技术创新产生“先促进，后抑制”的非线性影响。现有研究大部分都指出环境规制与绿色技术创新之间存在“U”型或倒“U”型的非线性关系。为更好地促进不同环境规制发挥其作用，不少学者对异质性环境规制展开研究。岳鸿飞［5］、肖权和赵路［6］分别应用固定效应模型、门槛模型和空间杜宾模型分析了异质性环境规制对绿色技术创新效率的影响。

国内学者在研究初期大多都选择门槛模型对环境规制与经济高质量发展之间的关系进行研究。童纪新和王青青［7］以雾霾污染为门槛变量构建单门槛效应模型，研究空间异质性对雾霾污染、环境规制与经济发展质量之间关系的影响。王群勇和陆凤芝［8］应用门槛模型得出环境规制对经济增长的促进作用存在区域异质性的结论。也有学者在前人的研究基础上，进一步采用空间计量模型对环境规制和经济高质量发展之间的关系进行研究。孔凡文和李鲁波［9］通过空间杜宾模型研究京津冀地区环境规制对经济高质量发展的影响，研究结果表明，京津冀地区环境规制对经济高质量发展均有促进作用。上官绪明和葛斌华［10］运用空间杜宾模型研究在不同城市规模和不同时期的情况下环境规制对经济高质量发展的影响，研究结果显示环境规制对经济高质量发展存在负向空间溢出效应。刘传明等［11］应用空间联立方程、广义空间三阶段最小二乘法研究环境规制与经济高质量发展之间的双向反馈效应。还有不少学者［12－14］采用中介效应模型研究某一影响因素在环境规制和经济高质量发展之间产生的中介效用。

学者们从不同视角研究了绿色技术创新与经济增长之间的关系。何小钢［15］用固定效应模型和随机效应模型研究绿色技术创新对可持续发展的影响作用，得出推动绿色技术创新不仅不会阻碍经济增长，反而会提高经济增长效率，同时改善环境污染的结论。吴文洁等［16］用广义OLS方法分析了绿色技术进步对经济增长影响的区域异质性。Meirun等［17］应用ARDL模型研究新加坡绿色技术创新对经济增长和二氧化碳排放的动态效应，研究结果显示，绿色技术创新与经济增长之间存在显著的正向关系。Shen等［18］研究政府设定经济增长目标的行为对区域绿色技术创新的影响，结果表明，经济增长目标的设定和自上而下的放大对绿色技术创新具有显著的抑制作用，这种抑制作用在经济增长较快、经济增长目标超额完成的城市更为突出。

综上所述，国内外学者对环境规制产生的经济影响进行了多方面的分析，但国内学者关于环境规制对经济高质量发展的影响研究所应用的模型主要集中在门槛模型、空间计量模型和中介效应模型上，主要考虑的是环境规制、绿色技术创新对经济高质量发展的单向影响作用，较少考虑到三者之间的相互作用和滞后作用。其次，关于区域异质性影响的研究通常采用地理划分的方式，缺少一定的针对性。环境规制和绿色技术创新之间的相互作用结果影响着经济高质量发展水平，若当地环境规制强度远大于绿色技术创新水平，这时“成本效应”大于“补偿效应”，环境规制阻碍绿色技术创新发展，进而影响高质量经济的发展，可见环境规制和绿色技术创新两个系统的协调程度对经济高质量发展起着至关重要的作用。基于上述研究空白之处，本文采用面板向量自回归（PVAR）模型对环境规制、绿色技术创新和经济高质量发展之间的动态相关关系进行研究，将三者纳入一个系统中，考虑三者间的内生性影响。并应用耦合协调度模型计算各地区环境规制和绿色技术创新的协调程度，根据耦合协调度结果进行分类，将各省（区、市）划分为高匹配地区和低匹配区，研究在不同协调状态下，环境规制、绿色技术创新与经济高质量发展之间的影响差异。此外，大多学者关于环境规制的测度指标只选用单一指标，但本文基于显性环境规制和隐性环境规制两个方面构建了更全面、科学的环境规制指标体系。

2 研究设计

2.1 变量定义

环境规制（ER）。本文采用熵值法计算各地区的环境规制强度。借鉴赵玉民等［19］的研究结论，将环境规制分为显性环境规制和隐性环境规制，显性环境规制又细分为命令控制型环境规制、市场激励型环境规制和自愿型环境规制。由于自愿型环境规制在我国还处于发展初期，发挥作用不大，本文暂不考虑自愿型环境规制的影响。有学者［13，20］采取因环境污染问题而接收的信访数衡量隐性环境规制，也有部分学者［21］根据Pargal和Wheeler［22］的研究，利用人均收入水平、受教育程度和人口密度对隐性环境规制进行衡量。关于环境问题接收到的投诉信访数可以衡量当地居民的环保参与度，而人均收入水平可以衡量当地的环保宣传力度和环保意识，收入水平越高的城市会更先注意当地的环保问题。基于此，本文构建如下环境规制强度评价指标体系（表1）。其中每单位污染排放物所征收排污费由各地区排污费与“三废”（工业废水COD排放量、工业二氧化硫排放量和一般工业固体废物产生量）加权和之比得到。为消除价格因素的影响，本文以2008年为基期，采用相关价格指数对排污费和人均地区生产总值进行平减。

表1 环境规制强度评价指标体系

绿色技术创新（GTI）。本文采用包含非期望产出的SBM模型衡量各地区绿色技术创新水平。非期望产出SBM模型假设有N个决策单元，记为DMUj，j＝1，…，N，每个决策单元都有n种投入X，m1种期望产出Ya，m2种非期望产出Yb。定义矩阵X、Ya、Yb如下：X＝［x1，x2，…，xn］∈Rn×N，Ya＝［ya1，ya2，…，yam1］∈Rm1×N，Yb＝［yb1，yb2，…，ybm2］∈Rm2×N，其中，X＞0，Ya＞0，Yb＞0。规模收益可变条件下的非期望产出SBM模型可表示为：

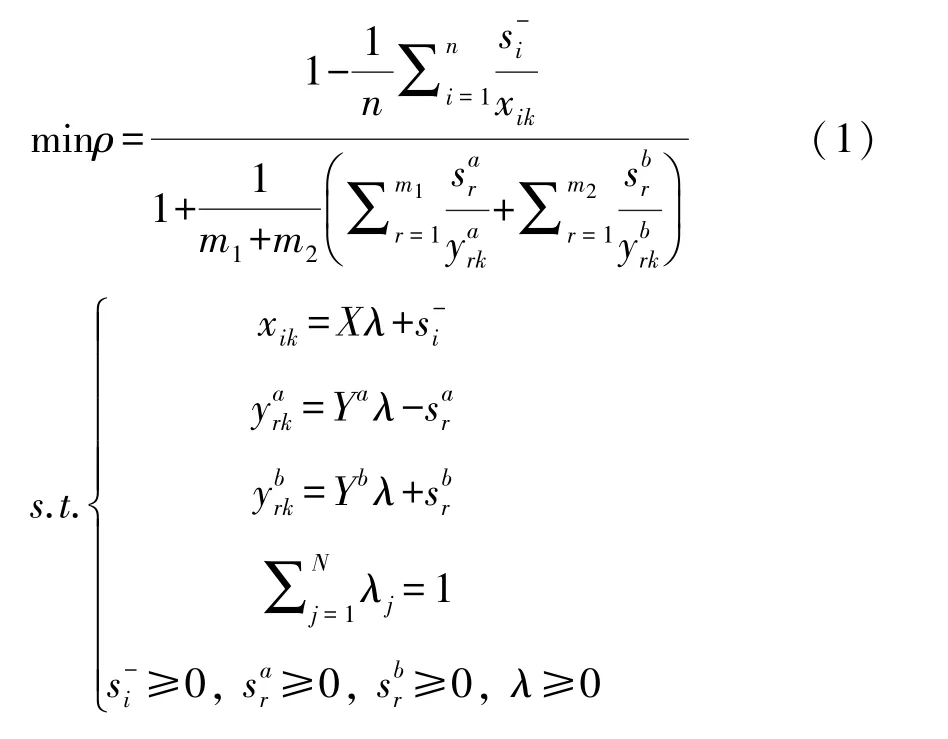
其中，ρ表示被评价决策单元DMU的效率值，s－表示投入松弛变量，sa表示期望产出松弛变量，sb表示非期望产出松弛变量，λ表示DMU线性组合系数。

从劳动力、资本和能源3个方面考虑技术创新过程中的投入要素，由于资本投入会产生积累效应，本文用R＆D资本存量作为资本投入的代理变量，R＆D资本存量采用永续盘存法进行核算。“三废”综合排放物指数由熵值法计算而得。为消除价格因素的影响，以2008年为基期，对规上工业企业新产品销售收入用相应价格指数进行平减，构建如下绿色技术创新评价指标体系（表2）。

表2 绿色技术创新评价指标体系

经济高质量发展水平（HQE）。根据新发展理念，本文构建包含创新驱动、协调发展、绿色友好、对外开放和全民共享5个一级指标及15个二级指标的综合评价指标体系，并采用熵值法计算各省（区、市）经济高质量发展指数（HQE）。

表3 经济高质量发展评价指标体系

耦合协调度（D）。根据环境规制（ER）和绿色技术创新（GTI）计算结果，利用耦合协调度模型计算两个系统的耦合协调度D。两系统耦合度C计算公式如下：

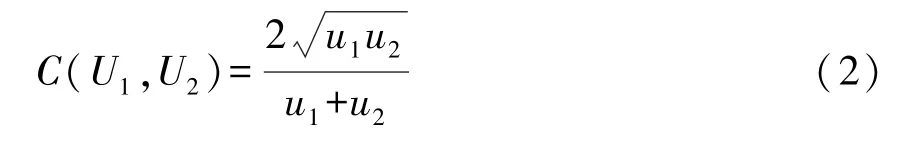
两系统协调度T计算公式如下：

其中，α和β分别表示两个系统的重要程度，且要求α＋β＝1。本文假定环境保护和技术创新同等重要，因此设定α＝β＝0.5。

最后，计算耦合协调度D，公式如下所示：

D的取值越大，表示两个系统的耦合协调程度越好。根据耦合协调度的计算结果，将平均值高于全国平均值的省（区、市）划分为高匹配区域，低于全国平均值的省（区、市）划分为低匹配区域。其中高匹配区域包括北京、天津、上海等11个省（区、市），低匹配区域包括河北、山西、内蒙古等19个省（区、市）。

2.2 模型设定

PVAR模型公式如下所示：

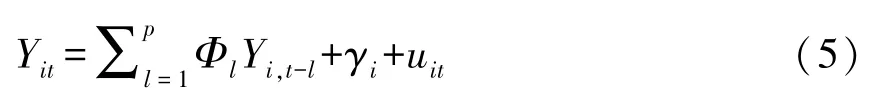
其中，Yit是由经济高质量发展指数（HQEit）、环境规制强度（ERit）和绿色技术创新效率（GTIit）构成的列向量，Yi，t－l是i地区滞后l期的经济高质量发展指数、环境规制强度和绿色技术创新效率，p表示滞后阶数，Φl表示滞后l期的斜率系数，γi为个体固定效应，即各省（区、市）之间的差异，uit为随机误差项。

2.3 数据来源

考虑到数据的可获得性，本文选取2008～2020年中国30个省、直辖市和自治区（除西藏、港、澳、台）为研究对象。所用到数据主要来源于《中国统计年鉴》、《中国环境年鉴》、《中国环境统计年鉴》、《中国税务年鉴》、《中国科技统计年鉴》、《中国能源统计年鉴》、《中国社会统计年鉴》（2009～2021年）。由于新冠肺炎疫情的爆发，异致2020年部分经济指标数据出现异常，但异常数据产生的影响不大，因此本文对其影响暂不做考虑。缺失数据采用插值法进行插补。

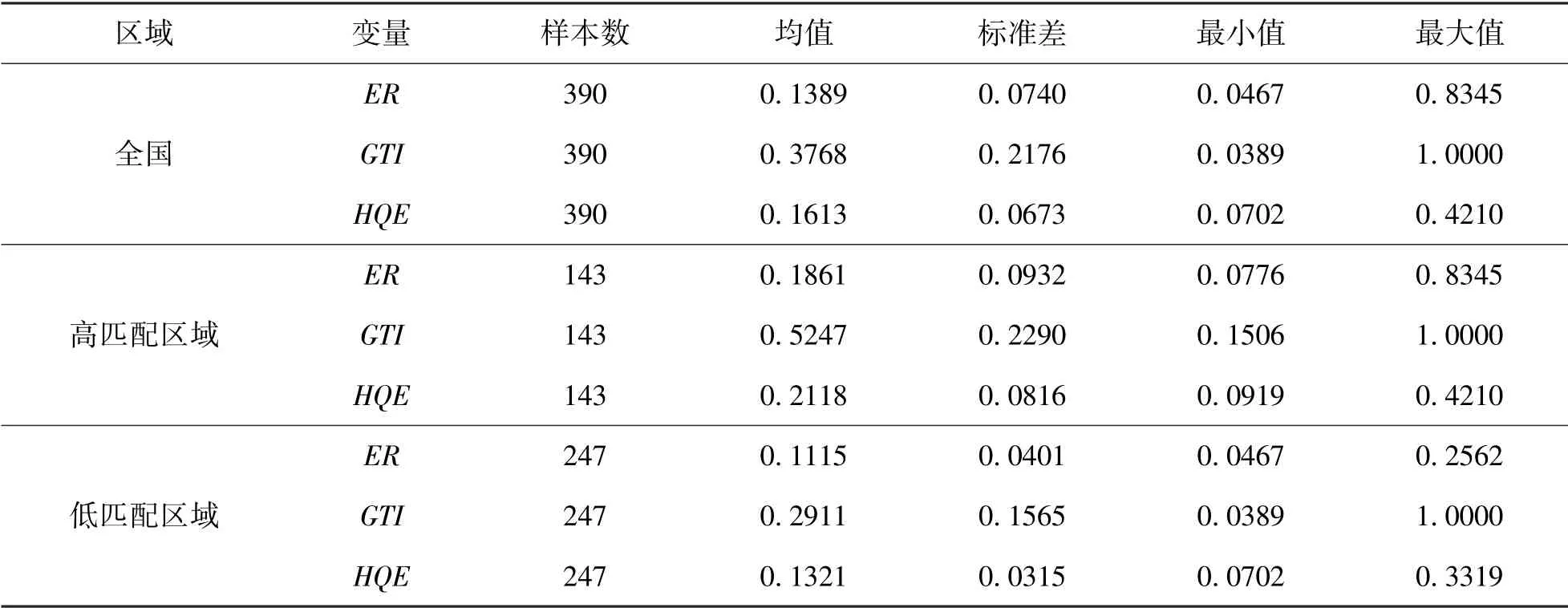
表4 描述性统计表

3 实证分析

3.1 平稳性检验及协整检验

为避免模型出现“伪回归”现象，应对变量进行单位根检验，检验变量是否平稳。由于本文选取的数据为n较大、T较小的短面板数据，因此选择IPS检验对变量进行单位根检验。

由表5可知，ER、GRI和HQE都没有通过IPS单位根检验，说明原始数据不具有平稳性。下一步对一阶差分后数据进行IPS单位根检验，检验差分后数据是否平稳。

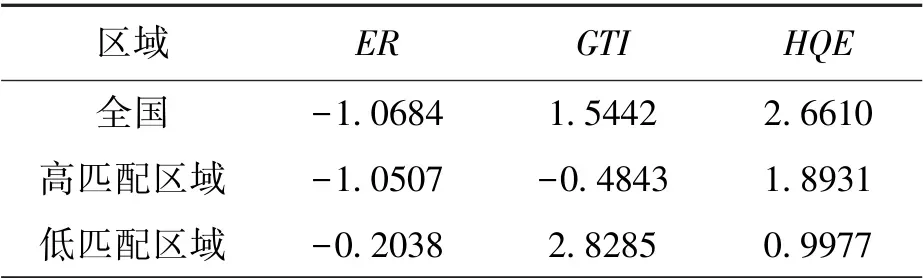
表5 原始数据IPS单位根检验

由表6可知，一阶差分后的各个变量在1%的显著性水平下可以拒接原假设，说明一阶差分后的数据为平稳数据。同时，可以看到ER、GTI和HQE都是一阶单整，变量之间存在同阶单整关系，可以进一步对变量进行协整检验，考察变量之间是否存在长期均衡关系。

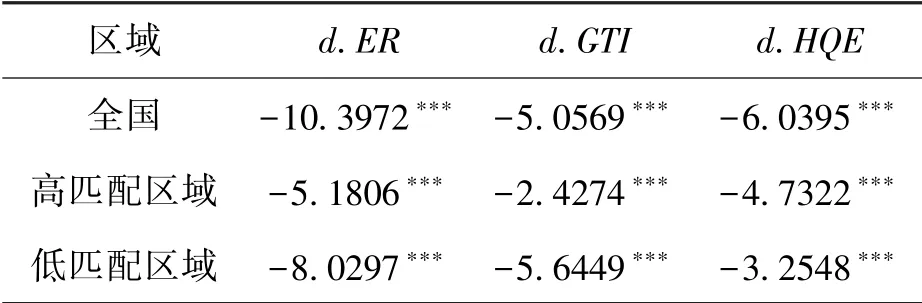
表6 一阶差分数据IPS单位根检验

对变量进行Pedroni协整检验，协整检验结果见表7。

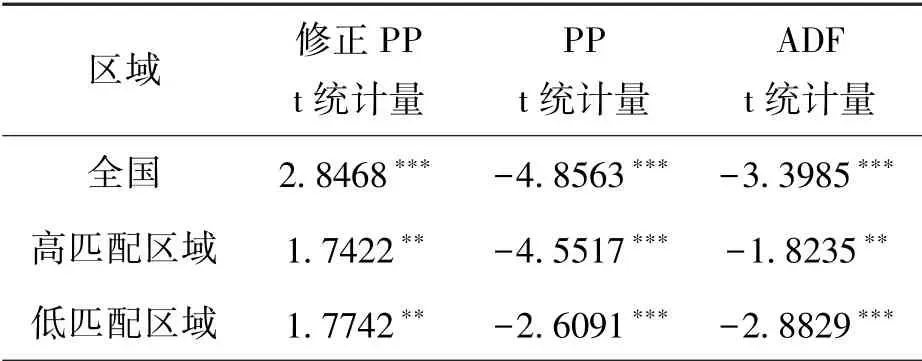
表7 Pedroni协整检验

由表7可知，至少在5%的显著性水平下可以拒绝原假设，即各变量之间具有协整关系，可以继续构建PVAR模型。

3.2 最优滞后阶数的选择

根据AIC值、BIC值和HQIC值最小原则选取模型的最优滞后阶数。

根据表8可知，全国的PVAR模型最优滞后阶数为1阶，高匹配区域的PVAR模型最优滞后阶数为1阶，低匹配区域的PVAR模型最优滞后阶数为2阶。

表8 最优滞后阶数选择

3.3 脉冲响应分析

由于内生变量的相互影响需要观察多个时期，PVAR模型的GMM估计参数没有实际经济意义，一般只关注其引出的脉冲响应函数和方差分解［23］。于是，本文仅针对GMM估计引出的脉冲响应结果和方差分解结果进行分析。

脉冲响应函数刻画了在其他变量不变的情况下，一个变量对另一个变量的一个标准差冲击的响应趋势。经过500次蒙特卡洛模拟得到的滞后10期脉冲响应图（略）。

图中横轴表示滞后期数，纵轴表示脉冲响应值，中间实线表示脉冲响应函数曲线，两侧虚线表示95%的置信区间。由脉冲响应图可以看出，脉冲响应函数在多期之后都趋近于0，说明本文构建的PVAR模型是稳定的。根据脉冲响应分析结果，可以得出以下结论：

（1）在全国范围内、高匹配区域和低匹配区域，环境规制、绿色技术创新和经济高质量发展水平面对来自自身的一个标准差冲击都产生了正向迅速的响应，说明环境规制、绿色技术创新和经济高质量发展水平都有着较强的自身惯性。

（2）面对来自绿色技术创新的冲击，环境规制在全国范围内和高匹配区域均产生了正向响应，响应值在第2期达到最大，最后响应逐渐减弱；低匹配区域内的环境规制也产生了正向响应，但响应值明显小于高匹配区域，且响应持续时间较短，第3期后响应值逐渐减小为0。面对来自经济高质量发展水平的冲击，环境规制在全国范围内和高匹配区域均产生了负向响应，负向响应在第2期后逐渐减小；在低匹配区域，经济高质量发展对环境规制一直产生正向的促进作用。说明在高匹配区域，环境规制政策、制度对当地环境状况起到显著改善作用，同时绿色技术创新水平的提高减少了工业污染物排放量，环境治理卓有成效，环境治理方面所需的投资占财政投入比例相对减少，环境规制强度在一定时期内不会增加。

（3）面对来自环境规制的冲击，高匹配区域内的绿色技术创新产生了正向响应，而低匹配区域内的绿色技术创新产生了负向响应。说明在环境保护与绿色技术创新发展相协调的省（区、市），环境规制给绿色技术创新带来的“补偿效应”大于“成本效应”，环境规制促进绿色技术创新发展，但在低匹配区域内，环境规制强度与绿色技术创新发展达不到协调状态，环境规制便对绿色技术创新产生了消极的抑制作用。面对来自经济高质量发展水平的冲击，3个区域范围内的绿色技术创新均产生了正向响应。

（4）面对来自环境规制的冲击，全国范围内和高匹配区域的经济高质量发展水平均在第1期后产生了负向响应；而低匹配区域内的环境规制给经济高质量发展水平带来了正向促进作用。说明高匹配区域的环境治理标准较高，环境改善已达初步成效，而低匹配区域内面临的环境问题依然严峻，环境规制强度的提升有助于加快当地的环保工作进度，促进绿色发展。面对来自绿色技术创新的冲击，高匹配区域内的经济高质量发展水平响应值在第1期达到最大，随后逐渐减弱；低匹配区域内的经济高质量发展水平响应值虽然为正值，但响应值明显小于高匹配区域，且响应值在第6期后逐渐减小为0。由于高匹配区域内的环境规制强度促进绿色技术创新发展，绿色技术创新效率提高，进而推动当地的经济高质量发展，而低匹配区域内的环境规制强度抑制绿色技术创新发展，阻碍了当地经济高质量发展进程，所以低匹配区域内绿色技术创新对经济高质量发展的促进作用小于高匹配区域。

3.4 方差分解分析

为了度量不同的结构冲击对内生变量变化的贡献程度，对预测误差进行10期方差分解。

由方差分解结果（表9），可以得到以下结论：

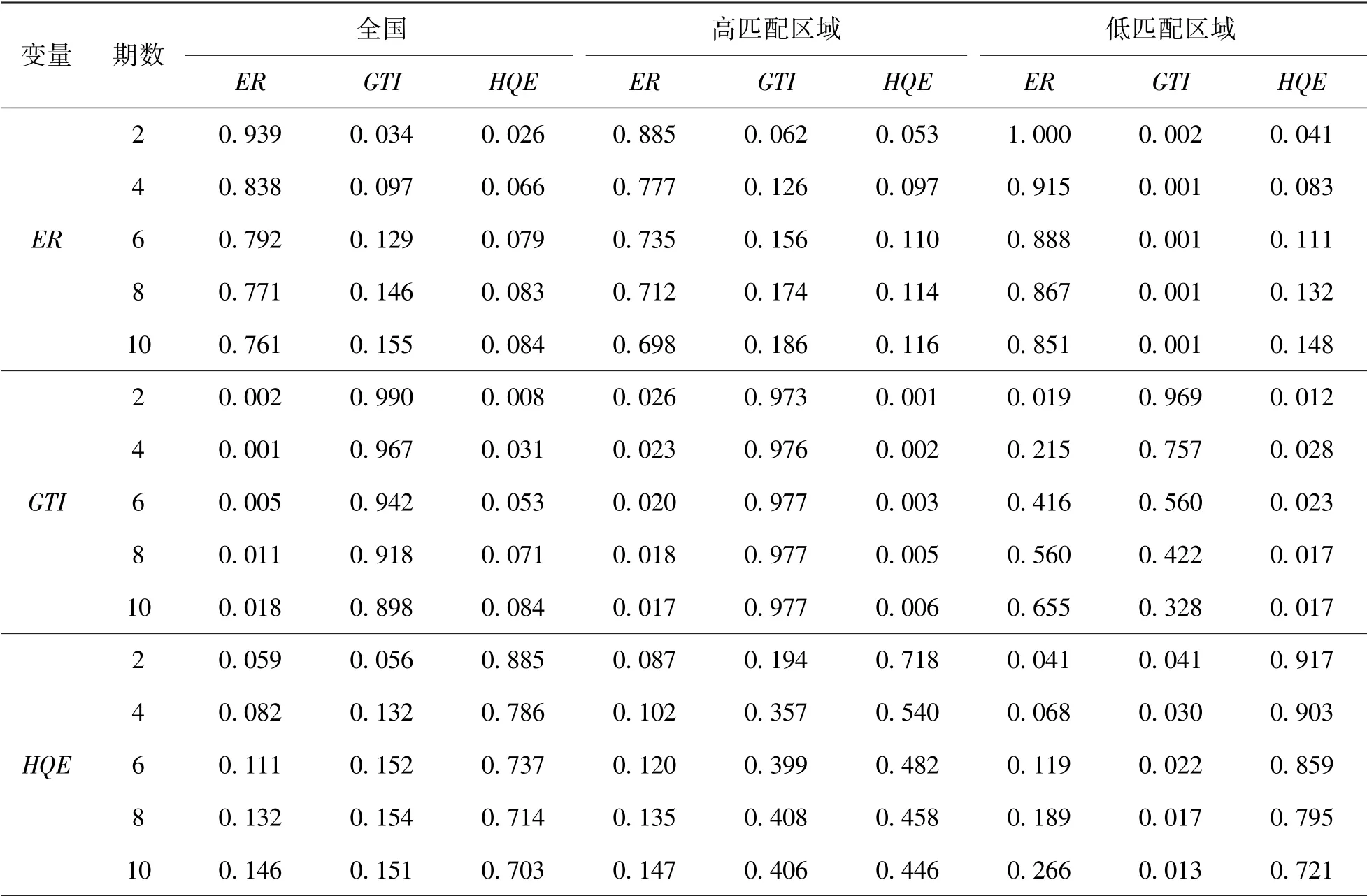
表9 方差分解结果

（1）高匹配区域的绿色技术创新对环境规制的方差贡献率高于低匹配区域，且低匹配区域绿色技术创新的方差贡献率持续减少，对环境规制变动的解释程度非常低；低匹配区域的经济高质量发展水平对环境规制的方差贡献率高于高匹配区域。绿色技术创新和经济高质量发展水平对环境规制的影响存在明显的区域异质性。

（2）低匹配区域内的环境规制和经济高质量发展水平对绿色技术创新的方差贡献率均大于高匹配区域。说明在环境规制和绿色技术创新协调程度较低的省（区、市），环境规制和经济高质量发展水平对绿色技术创新的影响更大，若当地政府不重视环保与技术创新间的协调性，盲目提高环境规制强度，会给绿色技术创新发展带来显著的抑制作用。

（3）高匹配区域的绿色技术创新对经济高质量发展变动的解释程度更高，低匹配区域的环境规制对经济高质量发展变动的解释程度更高，说明在高匹配区域的省（区、市）创新驱动力更强，高新产业更多更集中，对经济高质量发展起到了积极的促进作用。而位于低匹配区域的省（区、市）技术创新能力本就落后于全国水平，经济发展受外部影响更显著。

4 结论与建议

在国家创新构建现代经济体系推动经济高质量发展的背景下，本文构建PVAR模型研究了2008～2020年各省（区、市）环境规制、绿色技术创新和经济高质量发展之间的动态相关关系，并根据耦合协调度模型将30个省（区、市）划分为高匹配区域和低匹配区域，进一步对三者之间的关系进行区域异质性研究。根据模型结果可以得出以下结论：

（1）当前环境规制强度对绿色技术创新的影响存在区域异质性，在高匹配区域，环境规制促进绿色技术创新发展，而在低匹配区域，环境规制对绿色技术创新产生持续的负向作用。

（2）不论在高匹配区域还是低匹配区域，绿色技术创新都会促进当地的经济高质量发展，但相较于低匹配区域，高匹配区域内的绿色技术创新对经济高质量发展的促进作用更大，作用时间更长。

（3）在高匹配区域，经济高质量发展会给环境规制带来抑制作用，而在低匹配区域经济高质量发展对环境规制一直表现为促进作用，且低匹配区域的经济高质量发展对环境规制变动的解释程度更大，说明当地政府更依赖于经济发展现状和高质量发展指标制定环境保护政策，而忽视了环境规制和绿色技术创新之间的协调问题。

基于上述结论，结合不同区域的发展现状与不足，本文提出以下建议：

（1）时刻关注环境规制与绿色技术创新之间的协调程度。当前环境规制带来的“成本效应”较为显著，环境规制和绿色技术创新水平暂未在全国范围内达到高协调状态。因此，政府应加强宏观调控，时刻关注当地环境污染程度和技术创新水平，根据当地环境污染现状制定合理的环保法规和政策，避免因盲目加大环境规制强度而对绿色技术创新水平产生抑制作用，并加强对环境保护的宣传力度，号召当地群众积极参与环境保护事业，充分发挥各类环境规制的协同互补作用。

（2）加大绿色技术创新投入，实现绿色发展。处于低匹配区域的省（区、市）应加快构建区域协同创新体系，实现绿色产业转型，深化区域内绿色技术创新合作，积极引进绿色技术研发人员，逐渐完善绿色技术创新标准。实现环境规制强度与绿色技术创新水平的协调发展，进而带动地方经济的可持续发展。

（3）正确处理经济高质量发展与环境规制之间的关系。重视经济高质量发展与环境规制之间的双向反馈作用，将经济增长给环保事业带来的积极作用最大化，加快形成绿色发展方式，调整经济结构和能源结构，培育节能环保产业、清洁生产产业、清洁能源产业，要意识到绿色发展是我国的长期发展目标，环境保护也绝非一时之谈，避免在取得显著的环境治理成果后，放松对生态文明建设的要求。