重载铁路桥梁线桥偏心和道砟超厚的影响

王新让袁磊张岩李克冰李承君

1.国能朔黄铁路发展有限责任公司，河北肃宁 062350；2.中国铁道科学研究院集团有限公司铁道建筑研究所，北京100081

线桥偏心和道砟超厚是有砟道床重载铁路桥梁的常见问题。长期以来，受有砟道床线路结构养护清筛、捣固等作业影响，桥上道砟厚度不断增加，而运营列车横向作用力等效应则使得轨道与桥梁结构横向相对位置偏离设计状态，产生线桥额外偏心。

早期建设的大秦、朔黄等重载铁路多采用双片式简支T梁。根据TG/GW 103—2018《普速铁路桥隧建筑物修理规则》［1］：运营桥上线路中线与梁跨设计中线的偏差，圬工梁不应大于70 mm；运营桥上道砟厚度不应大于450 mm（框构桥除外）。线桥额外偏心过大主要影响列车活载在双片式简支T梁左右梁间的荷载分配；桥面道砟超厚一方面使得简支T梁承受的桥面二期恒载增加，另一方面可使列车活载的动力效应降低。

本文在对线桥偏心和道砟超厚情况下双片式简支T梁受力理论分析的基础上，结合现场实测数据，探讨了线桥偏心和道砟超厚对桥梁结构受力的影响程度，给出了相关病害的整治建议，可为桥梁病害整治维修决策提供参考。

1 道砟桥面双片式简支T梁活载偏载系数

1.1 活载弯矩偏载系数理论计算式

对于直线上双片式简支T梁，设计通常按每片梁承担列车荷载的1/2考虑，不计线桥偏心的影响。而对于曲线上梁，梁体布置通常以直代曲，线路中心线和梁体中心线采用平分中矢法布置，由此产生的线桥偏心效应采用活载偏载系数加以考虑。

对于运营状态线路平面位置变化产生的线桥偏心，其活载偏载系数目前没有明确的理论计算公式。本文在设计活载偏载系数理论计算式的基础上，对曲线上梁运营阶段线桥额外偏心下的活载偏载系数计算公式予以推导。假定［2］如下：

1）荷载在梁体顶面的分布为直线，见图1。图中l1、l2分别为线路中线至荷载分布线外侧和内侧边缘的距离，σ1、σ2分别为相应位置的荷载强度，e为梁顶处活载合力（N）作用点距l1+l2中点的距离。

图1 桥面荷载分布

2）荷载自枕底按1∶1的坡度扩散；

3）线路沿梁长为抛物线分布，即

式中：L为桥梁计算跨度；f为以跨度L为弦的线路中心线正矢，f=L2/（8R），R为曲线半径；eb为运营阶段产生的线桥额外偏心，以向曲线外侧偏心为正；x、y为以图2所示O点为坐标原点的纵向和横向坐标。

图2 道砟桥面桥梁与线路中心线的关系

由于沿梁长超高一致，活载分布也按式（1）计算。

根据荷载平衡原则，有

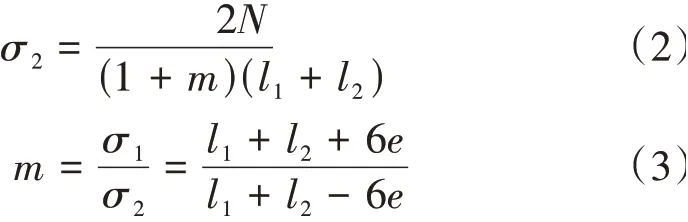
对于早期翼缘未设连接的双片式T梁，忽略横隔板的影响，认为两片梁独立作用。根据线梁几何关系，外梁承受荷载的宽度l1+f1-y，内梁承受荷载的宽度l2-f1+y，f1为设计状态桥梁中心线对线路中心线的正矢，对平分中矢法布置的梁有f1=f/2。任意截面上外梁和内梁承受的单位长度荷载Nox、Nix分别为

对荷载沿梁长积分，可求得任意截面弯矩，将其与直线梁任意截面弯矩对比，即可得额外偏心eb下曲线上外梁、内梁的活载弯矩偏载系数ηoM、ηiM分别为

当额外偏心eb=0时，式（6）即与TG/GW 208—2004《铁路桥梁检定规范》［3］给出的曲线上梁活载弯矩偏载系数计算公式一致。

对直线上梁，R=∞，且l=l、e=0，则m=1，有

式（7）与按杠杆法计算的直线梁荷载横向偏载系数表达式相近。这反映了前述推导对桥面荷载的横向分配本质上是按杠杆法考虑的。

1.2 活载弯矩偏载系数的影响因素

由理论计算式的推导可知，活载弯矩偏载系数主要与三方面因素有关［4-5］：①线上列车荷载合力N值及其偏心e值，其中N为列车竖向力和离心力的合力；②列车荷载在桥面的分布宽度l1、l2，由曲线超高、轨枕宽度和道床厚度共同确定；③线桥偏心值，包括曲线上梁设计线梁偏心值和运营阶段产生的额外偏心值eb。其中，前两项仅与桥面列车荷载和轨道结构的几何关系相关，第三项仅与线梁相对位置有关。线上列车荷载几何关系如图3所示。其中，W为列车静荷载；C为列车荷载离心力率；（1+μ）为列车荷载动力系数；H为列车重心至梁顶的距离；T为列车重心至轨顶的距离；t1为钢轨高度；t2为轨底至梁顶的距离；h为曲线超高；k为列车荷载合力作用点距线路中线的距离（以轨底平面为准）；i为列车静止时合力作用线距线路中线的距离，钢轨中心距取1.5 m。

图3 线上列车荷载几何关系（单位：cm）

在役铁路桥梁的计算跨径和曲线半径，以及采用的钢轨和轨枕的几何尺寸是确定的，服役车辆的重心高度通常也是确定的，曲线超高h可根据需要调整，道砟厚度会随着道床整修发生变化。重载铁路列车荷载离心力率C=V2/（127R），因而在役铁路桥梁活载弯矩偏载系数的大小主要与列车运行速度（V）、曲线超高、道砟厚度和线桥偏心有关。

以重载铁路常用跨度32 m简支T梁为例，其轨道结构采用Ⅲ型枕、75 kg/m轨，以曲线半径400 m、列车运行速度60 km/h、曲线超高100 mm、道砟厚度450 mm、线桥额外偏心0为基本状态，梁体在不同曲线半径、列车运行速度、曲线超高、道砟厚度、线桥偏心下的活载弯矩偏载系数见图4。

图4 活载弯矩偏载系数影响因素

由图4可知：在一定的列车运行速度和曲线超高下，随着曲线半径增加，外梁活载弯矩偏载系数减小，内梁活载弯矩偏载系数增大，且随着曲线半径的增大变化趋于平缓，当曲线超高较小而曲线半径较大时，活载弯矩偏载系数趋近于直线梁的1.0。在一定的曲线半径和超高下，随着列车运行速度增加，外梁活载弯矩偏载系数增加，内梁活载弯矩偏载系数减小，且随着行车速度的增大变化越趋明显，因而在设计计算时，外梁偏载系数取最大行车速度对应值，内梁偏载系数取平均行车速度对应值。活载弯矩偏载系数随曲线超高、道砟厚度和线桥偏心均呈线性变化：随着曲线超高增加，外梁活载弯矩偏载系数减小，内梁偏载系数增大；随着道砟厚度增加，外梁活载弯矩偏载系数增大，内梁偏载系数减小；随着向曲线内侧的偏心增大，外梁活载弯矩偏载系数减小，内梁偏载系数增大。其中，道砟厚度分别为250 mm和850 mm时的活载弯矩偏载系数相差约1%，说明道砟厚度对活载弯矩偏载系数的影响很小。

2 双片式简支T梁活载弯矩偏载系数精细化分析

如前所述，双片式简支T梁活载偏载系数理论计算式的推导未计横隔板等对荷载横向分配的作用，在对运营桥梁分析评估时可能偏离结构实际受力状态，有必要对结构受力进行精细化分析。

采用梁格法［6］对双片式简支T梁活载弯矩偏载系数进行精细化分析。以某重载铁路32 m简支T梁为分析对象，建立包含钢轨、轨枕和梁体的空间多层梁格模型（图5）。该桥曲线半径400 m，曲线超高100 mm，道砟厚度680 mm，线路相对桥梁向曲线内侧额外偏心310 mm，采用Ⅲ型枕、75 kg/m轨。

图5 线桥偏心下双片式T梁受力分析多层梁格模型

表1给出了分别按式（6）和梁格法计算的不同行车速度下偏心侧内梁与相应外梁的活载弯矩偏载系数计算值。在行车速度不大于70 km/h时，按式（6）计算的内梁活载弯矩偏载系数较梁格法偏大，相应地外梁活载弯矩偏载系数偏小，随着行车速度的增加，两者差异减小。在列车低速运行时，两者差异约为10%~15%，在列车运行速度达到80 km/h时，两者基本一致。

表1 线桥偏心下活载弯矩偏载系数计算结果

对该桥在实际运营列车作用下曲线内梁和外梁的活载弯矩偏载系数进行了测试，得到不同编组运营列车以不同速度通过时的活载弯矩偏载系数，并与理论值对比，见图6。

图6 实测活载弯矩偏载系数与理论值对比

由图6可知：实测内梁活载弯矩偏载系数随列车运行速度增加而减小，外梁活载弯矩偏载系数随列车运行速度增加而增大，与理论计算结果的变化趋势一致。相对而言，梁格法计算结果与实测值吻合程度更好，而式（6）的计算结果则较为明显地偏离了实测值。因而理论计算式更适合偏保守的设计包络计算（外梁取最高行车速度、内梁取平均行车速度），在对结构实际受力进行分析时则会带来一定偏差。

3 线桥偏心和道砟超厚对梁体受力的影响

以前述重载铁路32 m双片式简支T梁为分析对象，其道砟厚度680 mm，线路相对桥梁向曲线内侧额外偏心310 mm，不同状态下的主力组合（恒载+列车活载）跨中弯矩见表2。可知：设计状态曲线上32 m梁以外梁受力更为不利。运营过程中线路向曲线内侧的偏心一定程度上减缓了外梁受力的不利状态，仅计线桥偏心时，内梁和外梁跨中组合弯矩均小于设计最不利值。道砟超厚对内梁和外梁均存在不利影响，道砟厚度680 mm时，内梁和外梁跨中组合弯矩均大于设计最不利值，其中外梁弯矩20 552 kN·m较设计最不利值17 166 kN·m大20%。同时考虑道砟超厚和线桥偏心效应，内梁和外梁跨中组合弯矩分别为18 939 kN·m和19 221 kN·m，较设计最不利值分别大10%和12%。换算线桥额外偏心-310 mm时与道砟超厚270 mm时的内梁跨中组合弯矩相当。

表2 线桥偏心和道砟超厚下T梁跨中组合弯矩及其比较

对于线桥偏心和道砟超厚病害的整治，应根据病害的实际情况，以线路专业的轨道线形和标高调整为主，并根据实际运行列车的情况设置合理的曲线超高，采取措施增强轨道结构的横向稳定性［7］。

4 结论

1）在设计活载偏载系数理论计算方法的基础上，推导了考虑运营阶段线桥额外偏心的活载弯矩偏载系数计算公式，可用于线桥偏心状态梁体结构受力分析。

2）列车活载偏载效应与桥梁跨度、曲线半径、曲线超高的设置以及行车速度、道砟厚度、线桥偏心值有关。随行车速度增加，外梁活载弯矩偏载系数增大、内梁减小；道砟厚度对活载弯矩偏载系数影响很小；线桥偏心使得偏心侧梁体活载弯矩偏载系数增大。

3）实测列车活载弯矩偏载系数与采用多层梁格模型分析的结果吻合较好，但与理论计算式结果存在一定偏差。列车低速行驶时，理论计算式和梁格法计算结果相差10%~15%，车速80 km/h时两者基本一致。在对结构实际受力进行评估时，采用精细化分析的梁格法更为合理。

4）线桥偏心使得双片式T梁偏心侧活载效应增大，由于曲线上线路相对桥梁多发生向曲线内侧的偏心，对32 m梁来说在一定程度上缓解了设计状态更为不利的外梁受力状态；道砟超厚使得内梁和外梁的二期恒载效应均明显增大，对两片梁受力均不利。