基于离散-连续耦合方法的圆砾地层超深地连墙施工力学行为研究

申玉生，甘雨航，资晓鱼，董 俊，闵 鹏，张逸飞，王 进

(1. 西南交通大学交通隧道工程教育部重点实验室，四川成都 610031； 2. 中国科学院光电技术研究所，四川成都 610209； 3. 中铁第四勘察设计院集团有限公司，湖北武汉 430063； 4. 中国中铁四局集团城市轨道交通工程分公司，安徽合肥 230022)

0引 言

随着城市建设的高速发展，高层建筑基坑工程也朝着超大超深的趋势发展。大部分的基坑工程深度在10～20 m范围内，部分基坑开挖深度达到了40 m[1]。超深基坑常用的围护结构形式主要是地下连续墙或钻孔桩，围护结构的深度或桩径随基坑工程规模不断增大。围护结构作为保证基坑稳定与周边环境安全的第一道屏障，其施工阶段的稳定与后期基坑开挖安全稳定密切相关。

长期以来，基坑施工过程模拟分析普遍采用连续介质的计算方法，该方法能再现基坑施工过程中应力和位移的变化规律，但无法针对离散地层从细观角度揭示地层内部力、位移变化规律[2-3]。当前，部分学者根据工程地质特点，采用离散元法对基坑工程中相关理论技术问题进行了深度研究与剖析。吴凤元等[4]建立桩-钢支撑基坑颗粒流模型，对基坑开挖阶段桩体侧移及地表沉降等规律进行了研究。李博等[5]运用PFC2D对基坑封底阶段水下混凝土灌注工艺进行了模拟研究。周秋爽[6]基于三维离散-连续耦合原理，采用数值模拟和现场监测等手段研究了盾构隧道在新建隧道下穿施工扰动下的变形特性，并分析了夹层土变形破坏规律。申志福等[7]通过PFC2D研究了作用于支护结构上的土压力及其分布，同时将计算所得墙后地表沉降、墙体侧向位移及坑底土隆起规律与既有实测结果做了对比分析。周健等[8]利用PFC3D建立三维模型，分析了有、无复合土钉墙支护作用下基坑的应力场与位移场。贾敏才等[9]采用PFC2D，通过二次开发对基坑开挖变形进行了模拟。离散元法推广与应用能够对离散地层条件下地下工程问题进行较好求解。目前已有许多学者针对砂卵石地层地下工程运用离散元法进行研究[10]，但研究背景多依托于隧道及基坑工程[11-15]，而对地下连续墙成槽施工全过程力学行为尚未开展相关研究。

本文以昆明轨道交通4号线火车北站地铁车站工程为背景，基于有限差分法与颗粒流程序耦合的算法，建立三维离散-连续耦合模型，分析圆砾地层中单幅大厚度(1.5 m)超深(70 m)地下连续墙施工全过程力学行为，获得70 m深地下连续墙成槽过程颗粒变化特征及地层变形规律。本文研究成果对类似圆砾地层地下连续墙施工具有一定参考及指导意义。

1工程概况

昆明轨道交通4号线火车北站位于昆明市盘龙区北京路北站隧道与米轨交叉口，是地铁2号线、4号线、5号线的换乘车站。车站呈东西向布置，周边环境复杂，建(构)筑物较多。

火车北站车站总长345 m，标准段宽25.7 m，为地下四层16 m岛式站台车站。本站采用明挖顺作法施工，基坑埋深35.4～36.8 m。围护结构采用1.5 m厚地下连续墙，幅长5.5 m，平均墙深70 m，共计142幅(图1、2)。车站基坑竖向设置8道内支撑，其中第1、4、6、7道为钢筋混凝土支撑，其余为φ800×16钢支撑。

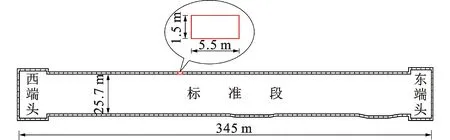
图1地下连续墙平面图Fig.1Plane View of Diaphragm Wall

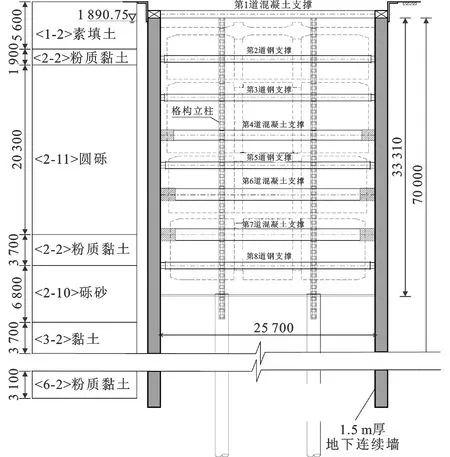
图2地铁车站横断面(单位：mm)Fig.2Cross-section of Metro Station (Unit: mm)

该车站地层分布自上而下主要为素填土、圆砾、黏性土、粉土、淤泥质土及泥炭质土(图2)。车站周边地质情况较为复杂，主要穿越以圆砾层为主的松散地层，自稳能力差且透水性强。地下连续墙成槽施工过程中，泥浆护壁性能易受影响。车站地下水与昆明市盘龙江联系紧密，地下平均水位为-4 m。

2离散-连续耦合计算方法

2.1FLAC-PFC耦合原理

早期耦合过程实现时FLAC、PFC需同时运行且精度较低。在FLAC3DV6.0环境下，PFC以插件形式嵌入到FLAC中，可以同时创建FLAC3D(连续)和PFC3D(离散)模型并实现两者的同步耦合计算(双向耦合)及实时可视化，能够真实地模拟离散-连续介质材料的相互作用[16]。

在FLAC-PFC耦合分析中，离散介质(球、簇)与连续介质(实体单元)的相互作用(力与弯矩)通过墙传递。墙体顶点附着于实体单元的网格点或结构单元的节点，达到同实体单元同步运动，协调变形的作用。

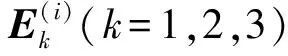
(1)

将顶点按顺序排列，依据右手定则可确定三角形面的法向量n(i)为

(2)

假定球体与墙面的法向重叠距离为Ui，当某一球体与墙面范围重叠时(Ui>0)，二者之间接触被激活，可得到每个墙接触点的单位法向量n(i)为

(3)

式中：di为球心Oi至墙接触点Pi的距离，di=‖Pi-Oi‖。

与此对应球-墙接触点Ci的位置为

(4)

式中：Ui=R-di，R为球体半径。

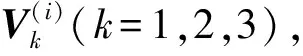
顶点加权因子ωk定义为与顶点相对三角形面

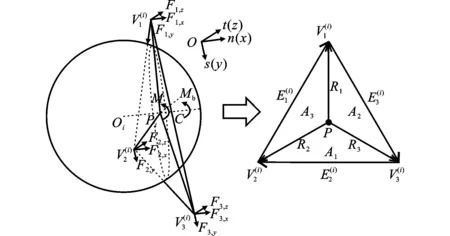
图3PFC墙体及耦合中力的传递Fig.3PFC Wall and Force Transmission in Coupling

积除以三角形的总面积，即ωk=Ak/A，则等式∑ωk=1恒成立，以保证从P到顶点外推值总和等于P处的值。当完全计算模式关闭时，接触力和平动刚度也通过这种方式外推到节点处。由于顶点力和潜在的顶点力矩在P处的总力矩可能不平衡，重心外推并不能确保外推力和力矩与瞬时接触力和力矩一致。

假定Rk(k=1，2，3)为P到3个顶点的力矩向量。施加在每一个网格点或者节点的力为Fk(k=1，2，3)，施加在接触点C上的力为F，接触点处由于黏结产生的力矩为Mb。由于接触点C和接触平面上点P可能不共点，所以作用在接触平面上的总力矩M为

M=Mb+(C-P)×F

(5)

当开启完全计算模式时，耦合方案确定完全一致的等效力系统，即

(6)

n为三角形面的单位法向量，沿着三角形面的剪切力矢量为Fs，即

Fs=F-F·n

(7)

单位切向量s为

(8)

建立局部坐标系，其中x方向与法向量n方向一致，y方向与切向量s方向一致。由于P点在三角形面上，Rk在x方向的分量上均为0，即Rk,x=0，则可直接确定局部坐标系中顶点力和力矩在x、y、z方向上的分量Fk,x、Fk,y、Fk,z和Mx、My、Mz，即

(9)

由于之前的重心加权项使力的y分量分布Fk,y=ωkFy，因此在三角形平面中最大接触力的方向上施加重心加权。此假设的结果导致方程组(10)有3个未知数。

(10)

此欠定方程组在无约束条件下有无穷多解，控制方程式不能明确地确定约束的性质来找到一个等效的系统。因此，为获得一个特解，需要提供额外的约束条件，紧随着实体单元或结构单元运动方程，以根据相应的网格点、节点位置和速度设置墙面顶点的位置和速度，约束条件为

∑Rk,zFk,z=0

(11)

该约束表示：如果开始时在局部z方向上的每个网格点或节点施加力，则从P指向局部坐标系中的三角形顶点向量的点积总和为0。所得到的合力随后被转换到全局坐标系并应用到适当的实体单元网格点或结构单元节点。

此时触发实体和结构单元更新，在实体、结构单元更新期间直接对网格点、节点添加刚度。当接触处存在旋转刚度时，通过将旋转刚度的大小除以∑‖Rk‖来确定等效的平移刚度，以确保系统稳定性。

2.2离散元细观参数标定

圆砾地层主要物理力学参数如表1所示。由于颗粒流离散元模型材料所需细观参数(法向接触刚度kn、切向刚度ks、摩擦因数f等)往往无法由土体宏观物理力学参数(弹性模量E、泊松比ν、土体抗剪强度指标c、φ)直接获得，因此首先需要对颗粒细观参数进行标定。如图4所示，建立三维颗粒试样进行三轴压缩试验。试样为直径10 m、高径比为2的圆柱体，颗粒数量为42 917个，颗粒接触采用线性接触模型。限于计算能力，本文在遵循实际工程圆砾颗粒级配规律的前提下对粒径进行了放大。在围压100、200、300、400、500 kPa条件下，经过不断调试，得到对应圆砾地层的理想颗粒细观参数见表2。

表1圆砾地层物理力学参数Table 1Physical Mechanics Parameters of Gravel Stratum

图4三轴压缩试验模拟Fig.4Triaxial Compression Test Simulation

图5和图6分别为试样在不同围压σ3下压缩所得应力-应变曲线及应力摩尔圆。由图5与图6可以看出，压缩试验模拟结果与实际土体宏观力学表现出较高的吻合性，因此能够在此基础上开展圆砾地层地下连续墙成槽施工的相关研究。

3三维耦合模型建立及参数确定

3.1模型建立

为便于计算，根据对称性原理，建立1/4模型对单幅地下连续墙施工全过程进行模拟。地下连续墙计算模型如图7所示，模型尺寸为20 m×80 m×35 m，其中上覆土体厚8 m，圆砾地层厚6 m，开挖槽段深度为70 m。模型侧面采用约束法向位移的边界条件，底部设置约束x、y、z方向位移的边界条件，顶面设置为自由边界。计算时对圆砾地层做离散处理，其余地层统一按黏性土层做连续处理，因此上覆土体、下伏地层以及浇筑混凝土均采用FLAC连续单元模拟，而模型中部圆砾地层采用PFC颗粒模拟，颗粒半径范围取0.15～0.2 m。

表2颗粒细观参数Table 2Micro Parameters of Particles

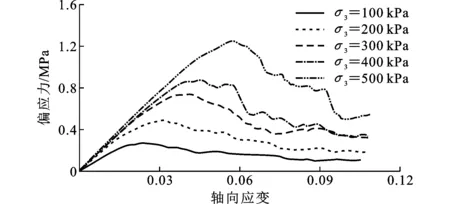
图5不同围压条件下试样应力-应变曲线Fig.5Stress-strain Curves Under Different Confining Pressure Conditions

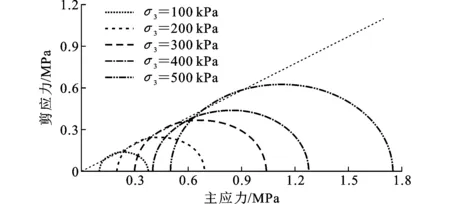
图6剪切强度线与不同围压条件下应力摩尔圆Fig.6Shear Strength Lines and Stress Mohr’s Circles Under Different Confining Pressure Conditions

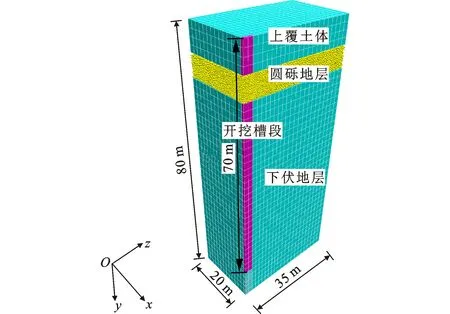
图7地下连续墙计算模型Fig.7Numerical Model of Diaphragm Wall

3.2参数选取

根据现场地勘资料，对黏性土层做统一合并简化，采用Mohr-Coulomb本构模型，浇筑混凝土采用线弹性本构模型，计算相关物理力学参数，连续单元物理力学参数见表3，离散元颗粒细观参数见表2。

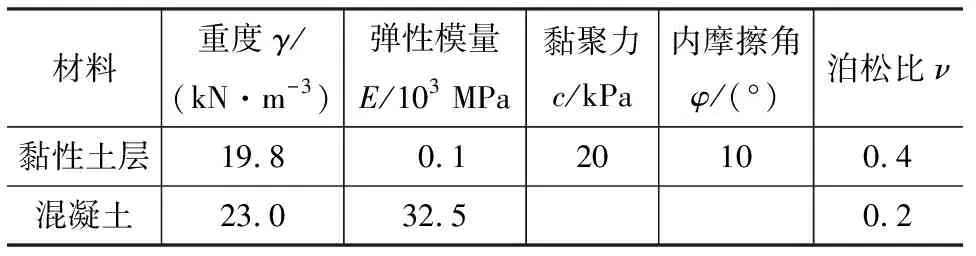
表3连续单元物理力学参数Table 3Physical Mechanics Parameters of Continuous Unit

3.3模拟步骤

3.3.1 泥浆护壁

槽段开挖通过对连续单元设置空模型并删除颗粒进行模拟，根据现场测试结果，泥浆重度取11 kN·m-3，采用梯度压力施加于连续单元节点。

实现泥浆护壁作用的关键是泥浆液压的施加。由于离散元模型由许多单个细微的离散颗粒组成，同时边界墙体亦不满足力-位移定律，无法直接施加压力于墙体。因此若参考连续介质模型中通过把梯度液压施加于单元节点的“直接方法”，将液压直接施加于单个离散颗粒或者墙体则无法较好地模拟离散元模型中泥浆对槽壁的护壁作用。对此，基于泥浆护壁机制，将槽壁表层颗粒通过平行黏结接触模型连接，可较好模拟槽壁表层泥皮，如图8(a)所示。此外，由于设置接触黏结，可将表层颗粒视为“连续柔性墙体”，进而实现泥浆液压的直接施加[图8(b)]。任意埋深处颗粒实际施加力f′由式(12)确定。

f′=pA′=γshA′

(12)

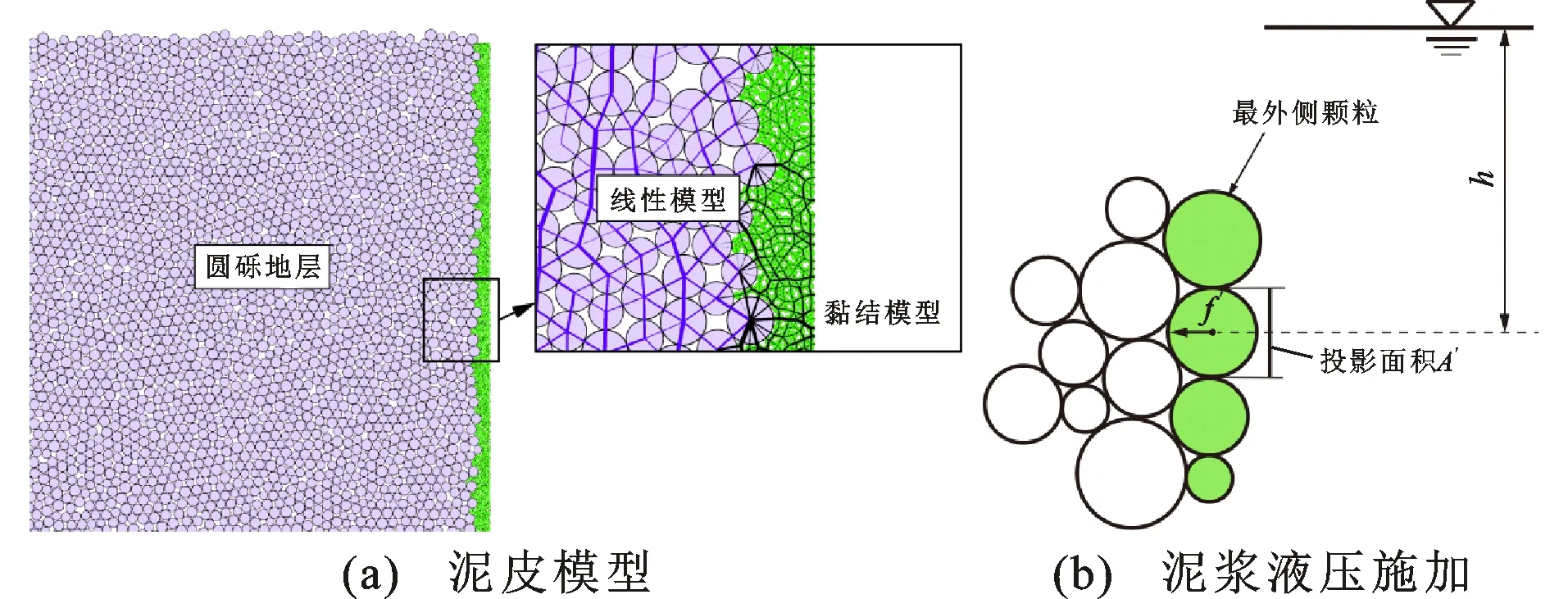
图8泥浆护壁作用实现Fig.8Realization of Wall Protection by Slurry

式中：γs为泥浆重度；h为颗粒中心至泥浆顶面距离；A′为颗粒沿液压施加方向的投影面积；p为压力。

3.3.2 混凝土浇筑和硬化

在水下混凝土浇筑阶段，最大混凝土压力与静水混凝土压力间存在流态系数，即混凝土最大侧压力与全高度静水混凝土侧压力之比。实测证明，该系数通常介于0.59～0.89之间，且随深度增加而减小。目前针对水下混凝土浇筑阶段模拟多采用梯度h压力分布形式与Lings等[17]于1994年提出的流态混凝土压力双线性分布模式。压力双线性分布如图9所示，其不同深度处压力p可表示为

(13)

式中：γc为流态混凝土重度；hcri为流态混凝土静水压力分布临界深度。

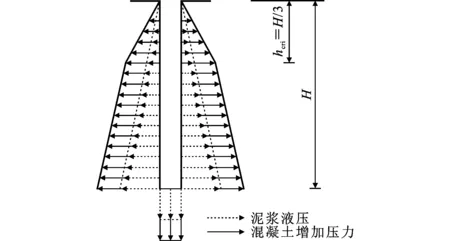
图9压力双线性分布Fig.9Bilinear Pressure Distribution

本文采用压力双线性分布模拟地下连续墙混凝土浇筑，流态混凝土重度γc取23 kN·m-3，分布临界深度取hcri=H/3≈23m，其中H为成槽深度。

混凝土硬化阶段移除施加的泥浆压力，并通过在开挖槽段设置实体单元进行模拟。

4地下连续墙施工全过程力学行为分析

4.1地层水平位移及应力分析

地下连续墙施工过程中，主要通过槽壁侧向变形来判断其稳定性，而地层水平应力分布则对槽壁稳定性具有显著影响。本节重点分析地层水平位移及应力在地下连续墙各施工阶段的分布特点及变化规律。

4.1.1 水平位移

图10为连续墙不同施工阶段地层水平位移云图及变化曲线，正值表示槽壁向槽段内变形，负值表示槽壁向槽段外变形。表4为各阶段地层水平位移及应力的最大值。

表4不同施工阶段地层水平位移及应力最大值Table 4Maximum Horizontal Displacement and Stress of Stratum in Different Construction Stages

图10地层水平位移变化Fig.10Horizontal Displacement Change of Stratum

槽段开挖后地层向槽段内侧变形，上覆土体、圆砾地层及下伏地层呈现不同的变形模式。上覆土体水平位移呈“悬臂式”分布，该层最大水平变形出现在顶部，最大位移约为3.9 mm；圆砾地层水平位移呈“抛物线”分布，该层最大水平变形出现在地层中部(12.2 m)，最大位移约为15.8 mm；下伏地层水平位移呈“悬臂式”分布，该层最大水平变形出现在与圆砾地层交界处(15 m)，最大位移约为8.3 mm。成槽阶段地层水平位移由大到小依次为圆砾地层、下伏地层、上覆土体，其中圆砾地层在成槽阶段出现最大水平位移，有诱发槽壁局部失稳的危险，工程施工过程中应予以重点关注。

在混凝土浇筑阶段，由于混凝土压力较大，地层逐渐向槽段外侧变形，地层水平位移整体呈“抛物线”分布，最大水平变形发生在槽段中部(40 m)，最大位移约为-38.2 mm，浇筑阶段地层水平位移关系由大到小依次为下伏地层、圆砾地层、上覆土体。随着混凝土硬化收缩，内挤变形逐渐减小，地层最终累计位移均小于5 mm。

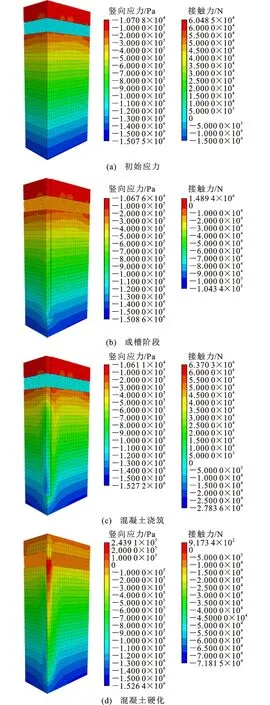
4.1.2 水平应力

图11为不同施工阶段地层水平应力及接触力云图。从图11可以看出：成槽阶段地层水平应力在槽段附近呈“凹”形分布，应力水平较初始应力有所下降；在混凝浇筑及硬化阶段，槽段附近水平应力呈“凸”形分布，应力水平出现明显增长。

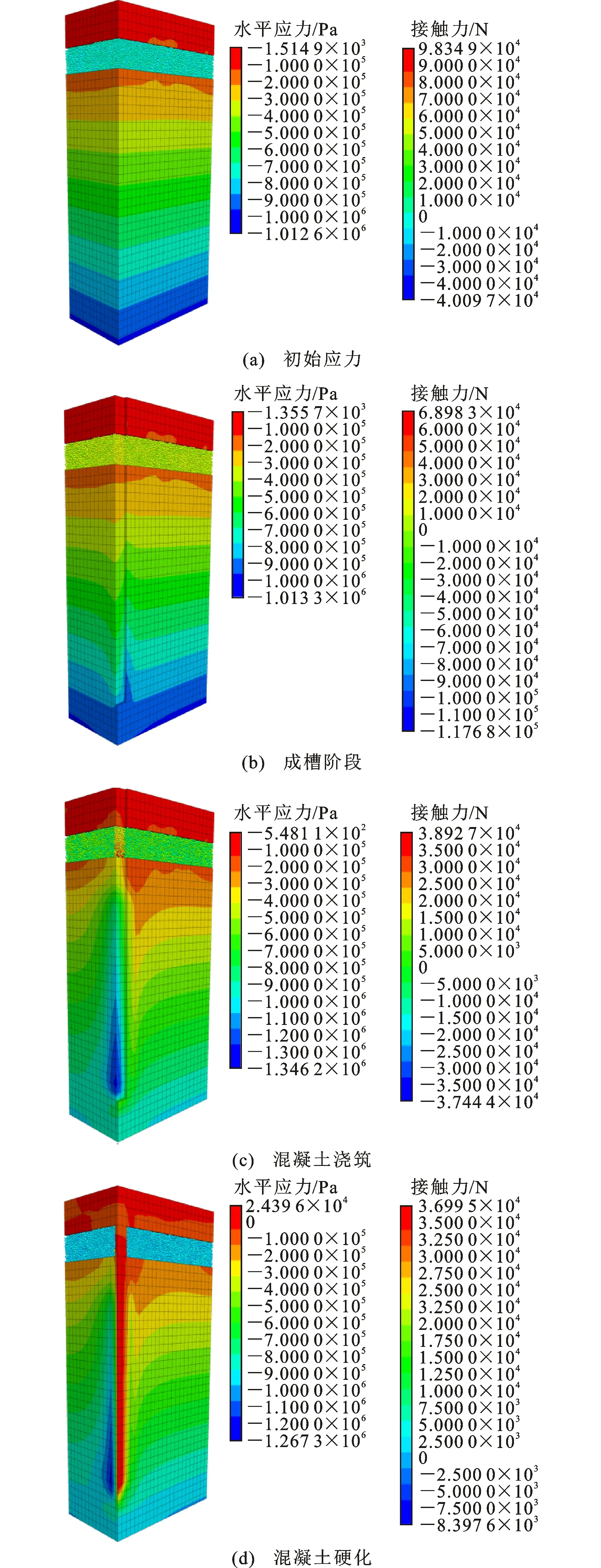
图11地层水平应力及接触力分布云图Fig.11Contours of Horizontal Stress and Contact Force Distribution of Stratum

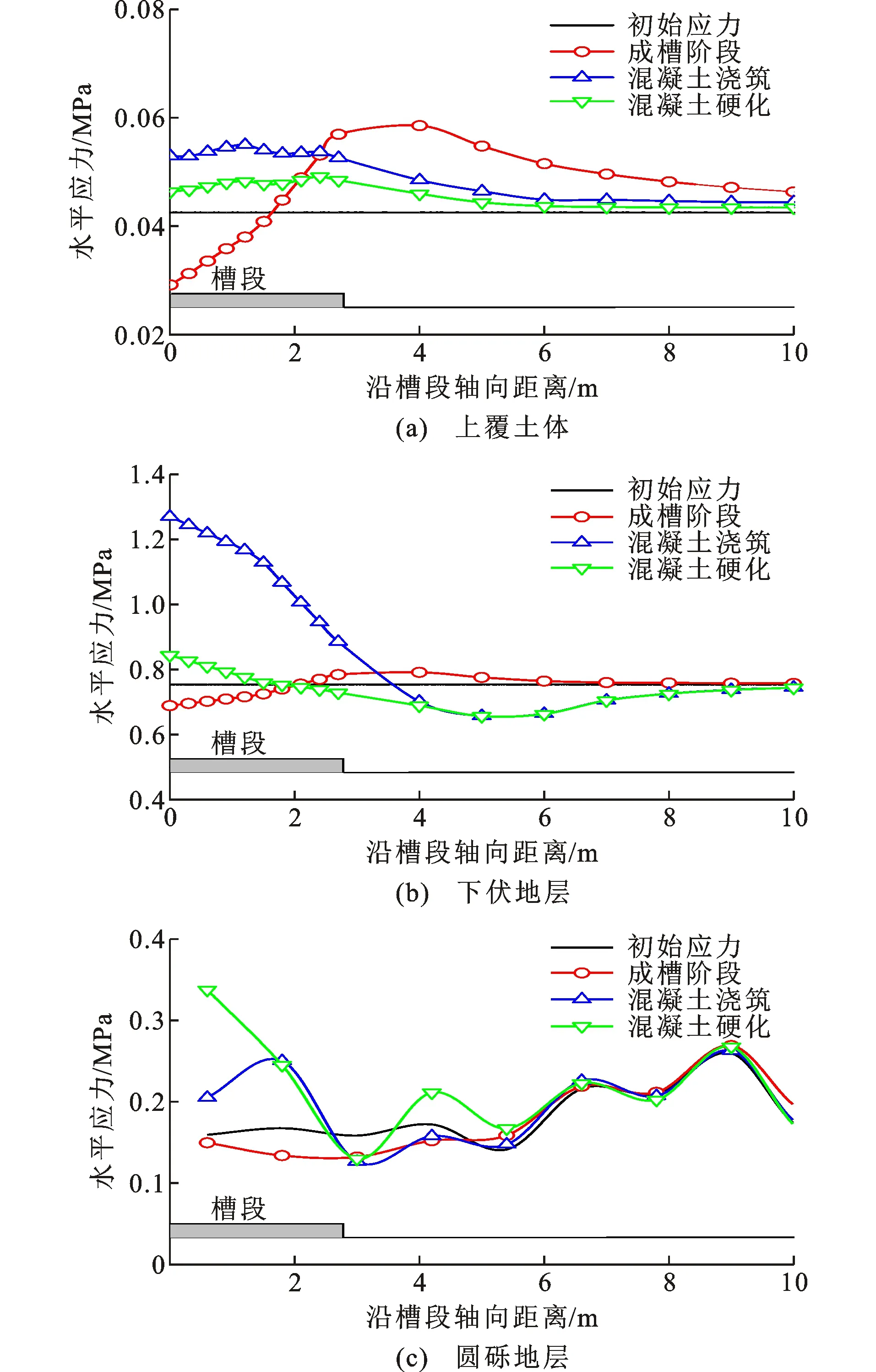
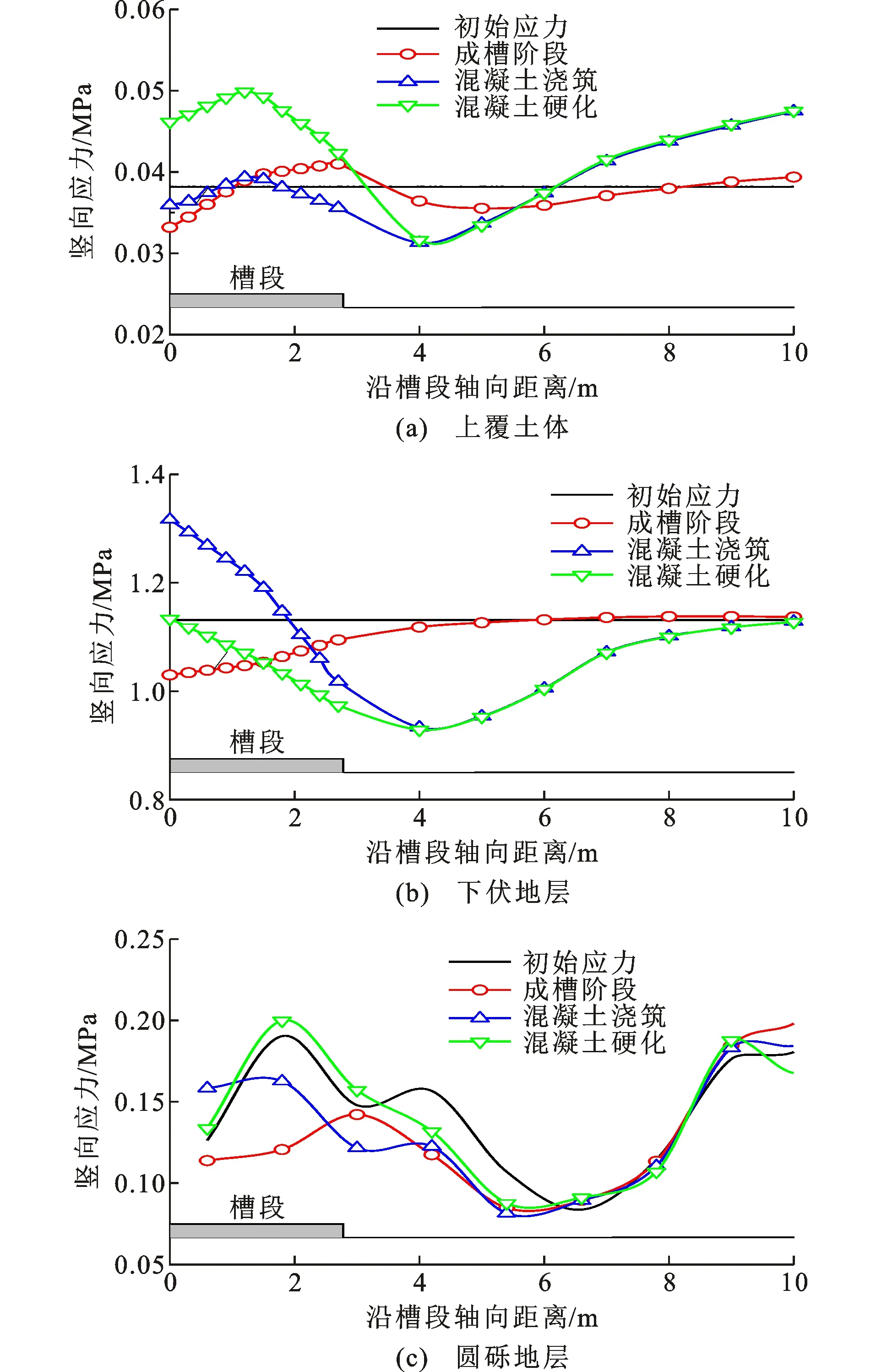
图12沿槽段轴向地层水平应力分布Fig.12Horizontal Stress Distribution Along Axial Direction of Groove

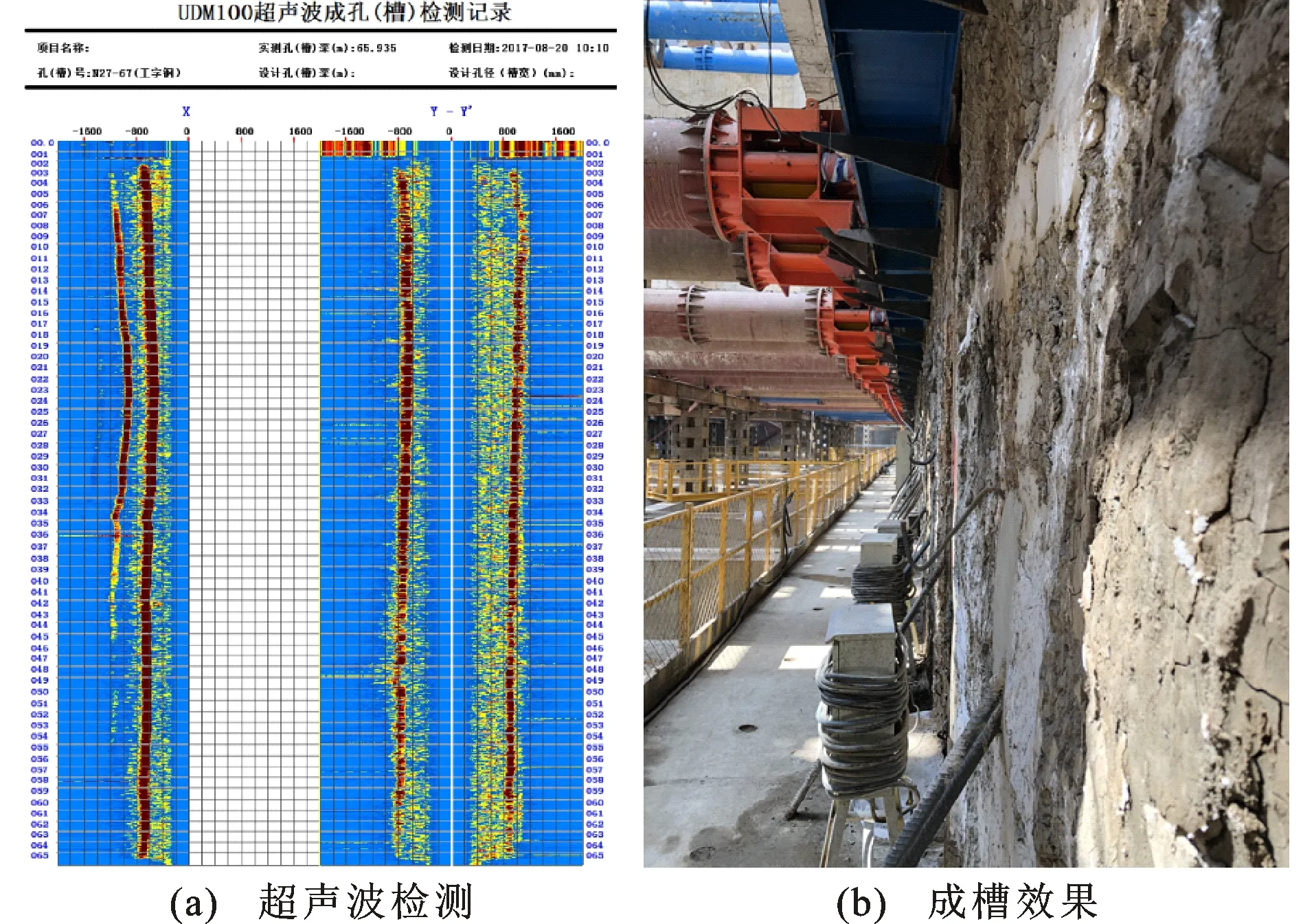
槽壁y=2、11、60 m处槽段轴向地层水平应力分布如图12所示。由图12(a)可知，在成槽阶段，由于土体开挖后应力释放，上覆土体0 m4 m后，水平应力逐渐趋于初始应力水平。槽段开挖对于上覆土体应力扰动范围大于10 m。在混凝土浇筑与硬化阶段，0 m

由图12(b)可知：成槽阶段下伏地层在0 m7 m后，水平应力逐渐收敛于初始应力水平，开挖对于下伏地层应力扰动范围大约为7 m。在混凝土浇筑与硬化阶段，下伏地层0 m

圆砾地层水平应力分布较为波动。由图12(c)可知，成槽阶段圆砾地层在0 m5 m后，无应力增长区域，说明该层无土拱形成，水平应力逐渐趋于初始应力。在混凝土浇筑及硬化阶段，该层同样出现应力增长，但分布仍比较波动。

综上所述，在成槽阶段黏性土层有土拱形成，能够较好发挥土体自承能力，而圆砾地层在该阶段无土拱形成。同时，成槽施工对于地层扰动范围由大到小依次为上覆土体、下伏地层、圆砾地层，而地层水平应力松弛范围由大到小依次为圆砾地层、下伏地层、上覆土体。在混凝土浇筑及硬化阶段，地层在混凝土压力挤压作用下均出现不同程度应力增长。

4.2地层竖向位移及应力分析

4.2.1 竖向位移

图13为不同施工阶地层竖向位移云图及地表竖向位移变化曲线。表5为各阶段地表沉降及竖向应力的最大值。

表5不同施工阶段地表沉降及竖向应力最大值Table 5Maximum Ground Settlement and Vertical Stress in Different Construction Stages

图13地层竖向位移变化Fig.13Vertical Displacement Change of Stratum

成槽阶段与混凝土浇筑阶段地层竖向变形主要集中于上覆土体及槽段底部，其中上覆土体变形模式表现为沉降变形，槽段底部变形模式表现为隆起变形。上覆土体地表竖向位移变化曲线如图13(d)所示，地表竖向位移曲线呈“三角形”分布，不同施工阶段地表竖向位移最大值点均位于槽壁边缘处，位移值与距槽壁边缘距离呈反比关系，与实测数据吻合。成槽阶段地表沉降最大值约为9 mm；混凝土浇筑阶段由于混凝土压力挤压，导致距槽壁边缘2～14 m范围内地表有向上隆起变形趋势，累计地表沉降值有所减小；当混凝土完全硬化，地表继续隆起变形，最终累计竖向位移值在1.5 mm以内。

4.2.2 竖向应力

图14为不同阶段地层竖向应力及接触力云图。从图14可以看出，竖向应力在成槽阶段仅于槽段底部出现明显减小，受成槽扰动相对较小，槽壁水平应力释放率比竖向应力释放率更大。在混凝土浇筑及硬化阶段，浅部地层出现一定应力增长，槽段底部竖向应力仍呈“凹”形分布。

沿槽段轴向地层竖向应力分布如图15所示。可以看出，各地层竖向应力在成槽阶段出现不同程度下降，而后逐渐趋于初始应力水平，仅上覆土体在2～3 m范围出现一个较小应力增长区域，地层竖向土拱效应不明显。在混凝土浇筑与硬化阶段，由于混凝土主要沿水平向对槽壁产生作用力，因此该阶段竖向应力增减规律不太明显。

在地下连续墙成槽过程中通过超声波测壁手段(图16)，对槽壁垂直度及塌孔缩孔等情况进行检测。结果表明：槽壁稳定性良好，已施工的地下连续墙侧壁均满足规范要求。

图14地层竖向应力及接触力分布云图Fig.14Contours of Vertical Stress and Contact Force Distribution of Stratum

5结语

图15沿槽段轴向地层竖向应力分布Fig.15Vertical Stress Distribution Along Axial Direction of Groove

(1)通过不同围压条件下对试样进行压缩试验所得应力-应变曲线，建立了试样细观参数与土体宏观参数间的关系，并通过调试得到了火车北站圆砾地层对应的理想细观参数。

图16成槽质量检测示意图Fig.16Sketch Map of Groove Quality Inspection

(2)超深地下连续墙成槽施工阶段槽壁出现向槽内卸荷变形，上覆土体与下伏地层水平位移呈“悬臂式”分布，圆砾地层水平位移呈“抛物线”分布。成槽阶段累计变形由大到小依次为圆砾地层、下伏地层、上覆土体，圆砾地层最大水平位移约为15.8 mm。在混凝土浇筑阶段槽壁向槽外反向内挤变形，并在混凝土硬化阶段逐渐收敛，地层最终累计水平位移均小于5 mm。

(3)连续墙成槽阶段的地层竖向变形模式为上覆土体沉降，槽段底部隆起。成槽阶段地表最大沉降发生在槽壁边缘，约为9 mm。随着混凝土浇筑及硬化，地表逐渐向上隆起变形，最终累计竖向位移在1.5 mm以内。

(4)成槽施工阶段地层水平应力与竖向应力在槽段处存在不同程度下降。黏性土层在槽段拐角附近有土拱形成，应力增加明显，圆砾层土拱效应不明显。在混凝土浇筑及硬化阶段，地层在混凝土压力挤压作用下均出现不同程度应力增长。研究成果成功应用于昆明地铁4号线火车北站工程，验证了超深地下连续墙施工全过程分析的成果。