利用磁流变弹性体对超材料梁进行带隙调控

张垚， 李金强， 宋智广， 李凤明

(哈尔滨工程大学 航天与建筑工程学院，黑龙江 哈尔滨 150001)

随着技术的发展，现代装备的服役环境日趋复杂，对其力学性能的要求不断提升，尤其是在航空航天、高速列车及舰船潜艇等领域的振动与噪声问题异常严峻。而振动与噪声对这些装备的服役安全性、可靠性以及操作人员的舒适性具有严重的影响。目前，结构振动的主被动控制已被广泛地研究和应用[1-3]。

近年来声子晶体和声学超材料领域[4-7]的兴起，提供了一种在特定频率范围内精确隔离结构振动的新方法。声子晶体和声学超材料是一类人工制造的具有特殊周期结构的复合功能材料，其具有独特的频带结构即通带与禁带。处于通带范围内的弹性波可以在结构中无损耗传播，而处于禁带范围内的弹性波无法在结构中传播。声学超材料所具有的这种独特的频带结构推动了声学隐身[8]、噪声控制[9]、波阵面操控[10]等领域的理论与技术革新[11-13]。

当结构振源的频率范围变化时，被动控制方案将不再适用。为了使声学超材料的功能具有更好的灵活性，研究者们使用了气压调节[14]、温度调节[15]、介质体积比[16]等物理方法来改变结构参数，进而改变结构的频带结构。除此之外，智能材料也已被用于解决各种复杂装备的振动问题。不同的智能材料如压电材料、电流变材料、磁流变材料、形状记忆合金等[17-22]，具有在力、电、热、磁等的作用下改变其形状和特性的能力。此类材料通过直接嵌入或粘接到结构表面的方式设计成结构，从而用作执行器、传感器和反馈控制器。如 Shen等[23]和Dong等[24]通过压电回路来调控声学超材料中的等效质量密度和等效刚度等参数，Luo等[25]将压电聚合物薄膜粘贴到声学超材料表面来调控结构的频带特性。Li等[26]利用压电材料和反馈控制策略所设计的声学超材料板具有零频带隙特性，通过主动调节可以获得优良的带隙特性。刘少刚等[27]利用外加磁场来调控以磁流变弹性体作为单、双包覆层的声学超材料的带隙特性。温舒瑞等[28]将基于磁流变弹性体的局域共振单元应用于超材料梁的设计并获得理想的低频宽频带隙。闻轶凡等[29]利用基于磁流变薄膜的磁固耦合声学超材料实现了声学超材料等效参数的非接触式主动控制。基于以上研究，本文设计了一种基于磁流变弹性体的超材料梁结构，可实现带隙特性与减振特性的非接触式控制。在此基础上，本文进一步研究了几何参数对主动超材料梁结构带隙特性的影响，发现通过改变振子拆分数量、振子大小及振子的位置偏移量可以实现对超材料梁带隙的有效调节。本文所提出的结构及研究内容丰富了主动声学超材料梁在低频减振领域的研究。

1 模型和方法

图1(a)为基于磁流变弹性体的超材料梁结构示意图。磁流变弹性体可通过外界磁场调节控制其剪切模量。图1(b)中周期晶格常数L=40 mm,质量块的边长Lm=20 mm，质量块与框架之间填充磁流变弹性体材料。

图1 基于磁流变弹性体的超材料梁结构及其单胞结构Fig.1 Schematic diagram of metamaterial beam based on magnetorheological elastomer

本文的计算采用有限元法，该方法已经广泛地应用于能带结构计算，在处理复杂结构时具有特殊的优势。在本文计算中所使用质量块及框架的材质为金属铝，其密度为2 680 kg/m3，弹性模量为69 GPa，泊松比为0.33。

关于磁流变弹性体MREs,本文采用磁偶极子模型[30-31]，其中铁颗粒的密度为7 890 kg/m3，橡胶密度为1 200 kg/m3。磁流变弹性体MREs的拉伸性能与剪切性能相似，其泊松比为0.47。外磁场的变化对剪切模量的改变为：

ΔG=36φμfμ0β2H2(R/d)3

(1)

式中：φ为铁颗粒在橡胶基体中的体积比；R为铁颗粒的颗粒半径；d为链中2个铁颗粒之间的间距；μ0为真空磁导率；H为外部磁场强度；μf=1为相对磁导率。在这里，假设d/R=2.5，ζ=1.202，β=1，体积分数φ= 0.27，无磁场的剪切模量G0=0.4 MPa。

2 计算结果和讨论

2.1 传输特性分析

基于COMSOL Multiphysics多物理场耦合仿真软件的固体力学模块，采用有限元方法对基于磁流变弹性体的超材料梁结构的带隙与减振特性进行了分析与讨论。在仿真分析中，对基于磁流变弹性体的超材料梁结构的所有组件均采用实体单元进行建模，并在1 000 Hz范围内对结构进行了足够精细的网格划分。所划分网格的总数为54 756。如图2所示，在梁的窄边边界处采用固定约束，而其他两侧的长边边界设置为自由边界条件。在图2所示的激励点施加垂直于面板的加速度ain，在加速度信号拾取点收集加速度响应信号aout。基于磁流变弹性体的超材料梁结构的透射率T，对数据做进一步的处理可以获得基于磁流变弹性体的超材料梁结构的传输特性：

(2)

图2 10×1周期基于磁流变弹性体的超材料梁结构及激励点及采集点设置Fig.2 Positions of excitation and measurement for the magnetorheological metamaterial beam with 10×1 periods

如图3中所示为基于磁流变弹性体的超材料梁结构在0～1 000 Hz内的传输曲线。通过观察图中的曲线，不难发现，图3中的曲线有一段急速衰减的区域，这表明弹性波在该频率范围内被有效地抑制。而在其他频率范围内，曲线没有明显的衰减，弹性波的传播未受到明显的抑制作用。由此，可以得出结论，本文所设计的基于磁流变弹性体的超材料梁结构能够在一定的频率范围内精确地隔离振动，该结构成功地打开了低频局域共振带隙。

图3 基于磁流变弹性体的超材料梁的传输曲线Fig.3 Transmission spectra of the magnetorheological metamaterial beam

2.2 结构带隙的主动调控

由于磁流变弹性体具有特殊的磁流变特性，即在外磁场作用下可大幅改变自身的剪切模量。基于这一特性，本文通过研究不同外磁场作用下的传输特征和振动特征来探讨基于磁流变弹性体超材料梁的带隙结构的主动调控。

为了更加直观地说明图3中传输曲线所示的带隙产生及减振机理，分别绘制了不同激励频率下基于磁流变弹性体的超材料梁及内部谐振器的振动模态，如图4(a)、(b)所示。所选取的激励频率460 Hz位于带隙范围内，观察发现激励点周围面板的振动位移明显大于其他位置，振动在周期结构的几个单元内有效衰减，弹性波的传播被抑制。此外，观察到由磁流变弹性体和振子所组成的谐振器的振动情况还可以发现，靠近激励源的谐振器的相对位移明显大于其他谐振器，即离振源较近的谐振器起着更重要的作用。所选取的激励频率620 Hz位于带隙范围外，不难发现，振动几乎没有衰减的在整个梁中传播。这些现象揭示了局域共振带隙的减振机理，即带隙频率范围内的弹性波在沿着基于磁流变弹性体的超材料梁的传播过程中，由于磁流变弹性体与振子所组成的谐振器共振模式被激活，振动能量被局域在谐振器上，面板的振动被成功地衰减和抑制。

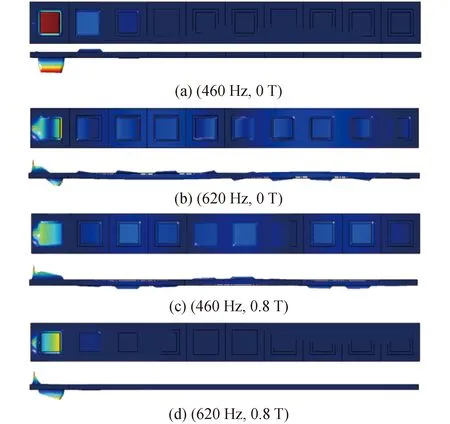
图4 基于磁流变弹性体的超材料梁在不同磁场强度及不同激励频率下的振动模态Fig.4 Vibration modes of the magnetorheological metamaterial beam under different magnetic flux density and excitation

图5展示了本文所设计的基于磁流变弹性体的超材料梁结构在在施加不同强度的磁场后，结构传输曲线的变化。由图5可以发现，随着磁场强度的增大，该结构的带隙逐渐由低频向高频移动，带隙的范围也逐渐增大，弹性波的衰减幅值未发生明显变化。实际上，这是因为随着磁场强度的增大，磁流变弹性体的剪切模量也随之增大，这会导致结构的固有频率向高频移动。为了便于直观比较，进一步绘制了磁场强度为0.8 T时超材料梁在不同激励频率下的振动模态，如图4(c)、(d)所示。观察并比较图4(a)、(c)以及图4(b)、(d)，发现可以通过调节外界的磁场强度，有效地抑制不同激励频率下基体梁的振动。

图5 基于磁流变弹性体的超材料梁在不同磁场强度下的传输曲线Fig.5 Transmission spectra of the magnetorheological metamaterial beam under different magnetic flux density

如图6所示，为了更直观地展示主动声学超材料梁在带隙拓宽与调控方面的优势，进一步计算了基于磁流变弹性体的超材料梁单胞结构在不同磁场强度下的固有频率，预测了其带隙变化范围[7]：

(3)

式中：f1与f2分别表示带隙的起始与终止频率；ω表示基于磁流变弹性体的超材料梁单胞模型的固有频率；m1、m2、m3分别表示单胞模型中磁流变弹性体、振子及基体框架的质量。由图6可以更加直观地发现，随着磁场强度的增加，带隙的上下边界频率均随之上升。

综上，通过对本文所设计的基于磁流变弹性体的超材料梁施加磁场后可以实现低频范围内带隙的可控调节，从而实现对低频振动的非接触式主动控制，可以拓宽超材料梁结构的应用范围。

2.3 几何参数对主动超材料梁结构带隙特性的影响

基于磁流变弹性体的超材料梁的单胞结构由支撑框架、磁流变弹性体填充层以及振子3部分组成，而这些部分具有独立的几何与材料参数，这些参数的选择会直接影响到所设计结构的减振性能。因此，本节针对一些主要的几何参数进行分析，通过对基于磁流变弹性体的超材料梁的传输曲线进行分析，研究这些参数对带隙特性的调控规律。

图6 基于磁流变弹性体的超材料梁的带隙区间随磁场强度的变化Fig.6 Band-gap bound frequencies of the magnetorheological metamaterial beam vs. magnetic flux density

在上文的基础上进一步研究了振子数量及排布对基于磁流变弹性体的超材料梁结构的带隙特性的影响。在保持振子的总质量不变的条件下，本文将振子分别拆分为2块和4块，其单胞结构模型如图7所示。需要说明的是，振子拆分后的单胞的结构尺寸和材料参数不发生变化。图7(a)中振子的长度和宽度分别为20和10 mm，图7(b)中振子的边长为10 mm。

图7 不同数量振子超材料梁单胞模型Fig.7 Multi-mass cell models of the magnetorheological metamaterial beam

图8显示了不同数量振子超材料梁的传输曲线。可以发现，随着单胞中振子拆分数量的增加，基于磁流变弹性体的超材料梁的带隙范围逐渐向低频移动，带隙范围变窄。进一步观察发现，结构的衰减幅值也随着拆分数量的增多而变小。图9展示了振子数量为4的超材料梁结构在不同场强下的传输曲线。观察发现，随着磁场强度的增大，超材料梁的带隙区间逐渐向高频移动，这表明拥有多振子的超材料梁的带隙特性也可以通过外界磁场进行有效调控。进一步将图9与图5相比较，可以发现外界磁场对多振子超材料梁的带隙调控作用减弱。综上，在振子总质量不变的情况下，振子数量的增加更容易获得更低频的带隙，但带隙的范围和衰减幅值会一定程度的减少，外界磁场对带隙的调控作用也会减弱。

图8 不同数量振子超材料梁的传输曲线Fig.8 Transmission spectra of the magnetorheological metamaterial beam composed of multi-mass cell

图9 振子数量为4的超材料梁在不同场强下的传输曲线Fig.9 Transmission spectra of the magnetorheological metamaterial beam composed of 4-mass cell under different magnetic flux density

质量块的大小对超材料梁结构的带隙特性具有重要影响，以下研究了质量块大小的影响。保持振子的其他参数不变，改变振子的尺寸，取其高度分别为6 mm和8 mm。计算基于磁流变弹性体的超材料梁的传输曲线随振子大小的变化如图10所示。由图中可以看出，随着振子高度的增加，质量块的质量随之增加，超材料梁结构的带隙范围向低频区域移动。这是因为，随着振子质量的增加，磁流变弹性体与振子所组成的谐振器系统的固有频率变小，所产生的局域共振型带隙的范围也向低频移动。因此，可以通过改变振子的尺寸实现更低频率的振动控制。

同样，保持振子的其他参数不变，改变振子的位置，分别偏移 1 mm和2 mm。图11绘制了基于磁流变弹性体的超材料梁结构在振子位置居中与偏移后的传输曲线。通过对图11中传输曲线的观察与对比，可以发现，振子位置偏移之后，第1阶带隙的起始频率未发生明显的改变，但终止频率随着偏移距离的增加而逐渐向低频移动，第1阶带隙的范围逐渐变窄。值得注意的是，振子的位置偏移之后，产生了新的带隙。并且带隙的宽度随着偏移量的增加而增大。此外，计算后发现，振子偏移之后，总的带隙宽度会一定程度增大。因此，可以通过调节振子位置的偏移量，产生更加丰富的带隙以及拓宽带隙的范围。

图10 超材料梁结构的传输曲线随振子大小的变化Fig.10 Transmission spectra of the magnetorheological metamaterial beam under different thickness of resonator

图11 超材料梁结构的传输曲线随振子位置偏移时的变化Fig.11 Transmission spectra of the magnetorheological metamaterial beam under different mass position offsets

3 结论

1) 将磁流变弹性体与振子组成的谐振器嵌入基体梁结构后，可以打开十分明显的局域共振型带隙，基体梁结构的振动在带隙范围内被显著衰减。

2)对本文所设计的基于磁流变弹性体的超材料梁施加磁场后可以实现低频范围内带隙的可控调节，从而实现对低频振动的非接触式主动控制，拓宽了超材料梁结构的应用范围。

3) 本文研究了几何参数对主动超材料梁结构带隙特性的影响，发现通过改变振子拆分数量、质量块的大小及位置偏移量可以实现对超材料梁带隙特性的有效调节。