类手性拉胀型声学超结构的设计及隔声特性研究

李鸿泽， 刘琪,2， 杨金水,2， 佟丽莉

(1.哈尔滨工程大学 航天与建筑工程学院，黑龙江 哈尔滨 150001； 2.哈尔滨工程大学 青岛创新发展基地，山东 青岛 266000)

噪音污染一直是工程界密切关注和着力解决的热点问题。在建筑方面，机械振动等噪音会造成声污染进而影响操作人员的身心健康，同时也会对周围的环境产生不良影响[1]。在军事方面，现代化的无人机、航母和武装坦克等各种军事装备需应对许多复杂环境的挑战[2]，与此同时还要使随之搭载的大量精密仪器和高精度设备能正常使用。因此，对降噪隔声技术的需求越来越高。而声子晶体由于其独特的隔声特性[3]走入大众视野。

声子晶体通常是弹性常数及密度周期分布的材料或结构，是把弹性固体周期排列在其他固体或流体介质中形成的一种功能型材料[4]。通过与光子晶体进行比较，人们发现在弹性波处于周期弹性复合介质中进行传播时，也会产生和光子带隙相似的弹性波带隙[5]，从而提出了声子晶体的概念。弹性波在声子晶体中传播时，受它内部结构的影响，在一定频率带隙内的传播会被阻止，而在余下频率的通带内可以无损耗传播。一般研究认为，声子晶体带隙产生的机理有2种:布拉格散射型和局域共振型[6]。布拉格散射型结构是其周期性起着主导作用，当入射弹性波波长和晶格常数约等时，结构就会受到强烈的散射。而局域共振型声子晶体的概念由刘正猷[7]在Science上提出，他们把硅橡胶包裹铅球按简单立方晶格的样式排列在环氧树脂基体中，进行了相应的实验。结论证实其具有低于400 Hz的低频带隙，比同样尺寸的Bragg散射型声子晶体的第一带隙频率降低了2个数量级。所以局域共振型声子晶体的主要特点是带隙频率远低于相同晶格尺寸的布拉格带隙从而实现了“小尺寸控制大波长”[8]。同时，带结构中存在平直带且内部波场存在局域共振现象，带隙由单个散射体的局域共振特性决定，而与它们的排列方式无关，带隙宽度随填充率的增加而单调增加[9]。

菲斯拉格[10]发现了介电常数和微导率都为负值的超常电磁介质，从而在理论上预测了反常现象。而后随着声子晶体之类的人工周期结构研究领域的不断发展，声学超材料的超常物理特性也开始受到广泛关注。由特殊设计的人工声学结构单元周期性排列在弹性介质中，可以获得具有与自然界中物质截然相反的物理性质的材料结构都可称为“超材料”[11]。Li等[12]提出声学超材料概念，把由软硅胶构成的散射体埋入水中构成了固-液声子晶体，并且在某些频率范围内其等效质量密度与等效体积模量均为负，即实现了“双负”特性。Li[13]等研究纯固体材料的三组元局域共振型声子晶体的等效参数，发现在带隙内表现出负等效质量密度特征。Fang等[14]研究周期阵列的亥姆霍兹共振器组成的一维声子晶体时发现，这种一维声子晶体在其局城共振带隙内表现出负等效模量。Sheng等[15]在对局城共振型声子晶体的等效介质理论进行研究时指出，局域共振单元会让声子晶体整体的等效质量密度出现变化，在一定条件下可以使质量密度表现为负值。Yun等[16]发现了一种粘弹性双负特性超材料。Wang等[17]发现了二维粘弹性阻尼型声学超材料的粘度对带隙内外的衰减大小的影响。声学超材料的研究历史比声子晶体的历史要短，目前主要的研究集中在完善研究方法体系[18]和研究方法，现阶段发展较为成热的算法是等效介质法。此外研究还集中在对超材料进行结构设计。

手性这一词最初存在于有机化学和原子物理中，手性结构自身与其镜像不能够重合，就好比人的左手和右手一样，这种结构破坏了空间结构的左右旋转对称性，增强了各向异性，在光学中这会产生一系列有趣的现象，如很早就已经发现的双折射、旋光现象等[19]。手性固体结构由Wojciechowski[20]提出，与普通材料结构相比，手性结构具有负泊松比特性[21-23]，具有很好的性能，传统结构在受压时受力方向会收缩，在另一个方向会膨胀，而负泊松比材料一个方向受压，另一个方向也会发生收缩现象。而当外力作用方向相反，即如果让材料在一个方向产生拉伸变形，材料另一个方向也同样会产生膨胀变形。具有这种特性的材料称为拉胀材料[24]。各研究都表明，手性结构在静力学、动力学都具有良好的特性，近年来已成为材料研究的热点问题，将手性结构的基本形式与超材料理论结合，有望为结构减振降噪提供一种新的设计思路与实现方式。

近年来，国内研究学者从工程实际需求出发，利用许多新型多功能复合材料力求让结构表现出轻质高刚度特性。文献[25-29]在超轻多孔结构、点阵结构、蜂窝夹层结构等功能结构和材料的相关研究领域开展了许多研究，主要的研究表现在结构的加工和制备以及静力学性能的表征和优化、结构的构型创新优化等方面。已有的研究表明，利用传统减振降噪方法对轻质高刚度结构引起的振动抑制效果和隔声性能都无法满足需求，因此就要求研究时结合声学超材料和手性[30]拉胀结构，引入高阻尼单元，在不降低结构高刚度特性的基础上，最终使高刚度、高阻尼特性融合[31]，使结构的减振降噪性能有一定的突破。

1 类手性拉胀型结构模型

类手性声学超结构是由局域共振型声子晶体错位堆叠形成的，然而通常结构隔声能力下降是由结构受力后出现损坏造成的，想让整体结构保持稳定的隔声性能，就要让结构具有更好的力学性能。将拉胀结构和手性结构的理念应用于错位堆叠的声子晶体中，可以让整体结构在受力过程中产生有限位移或扭转，而隔声部分不受影响。

声子晶体在受到手性结构的启发后，应用叠合梁型声子晶体，声子晶体单胞结构如图1所示。为保障其局域共振的特性，结构单胞由散射体1、包覆层1、散射体2、包覆层2和基体5部分组成，具体结构参数如表1所示，其中散射体1为边长为a1的正方形钢块，散射体2厚度为c，是外边长为a3，内边长为a2的正方形框架。包覆层由叠合梁型结构组成，为保障局域共振的特性，整个包覆层都采用软橡胶材料。包覆层1左右两侧为类手性结构，其中由厚度为b，高度为d，角度为45°的支杆连接中间半径为R的圆形结构。在上下两侧双箭头型结构中，上层箭头宽度与高度均为f1，中部空隙高度为f2，下层箭头高度为f3，宽度为f5，下部空隙高度为f4。包覆层2由长为f，宽为g的2个小矩形结构组成。基体在外边长为a5，内边长为a4的正方形框架基础上，在左右两侧设置弧形内陷，中部最大宽度为e。

表1 结构参数Table1 Structural parameters

对整个结构而言，纵向分为5层结构，以及顶部和底部的平板，具体结构形式如图2所示。平板厚度为h，结构整体宽度为t。结构层中1层、3层、5层为声子晶体结构，声子晶体单胞横向间距为i，2层、4层为软橡胶方形框架，框架水平方向均设置弧形内陷，中部最大宽度为e，具体材料参数如表2所示。

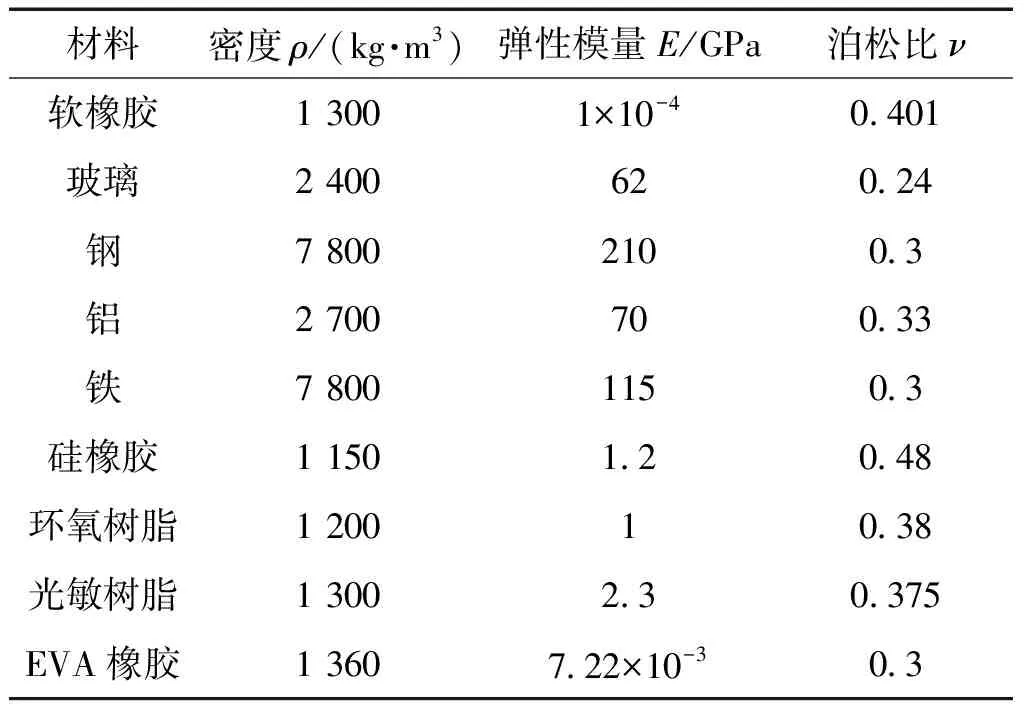
表2 材料参数Table2 Material parameters

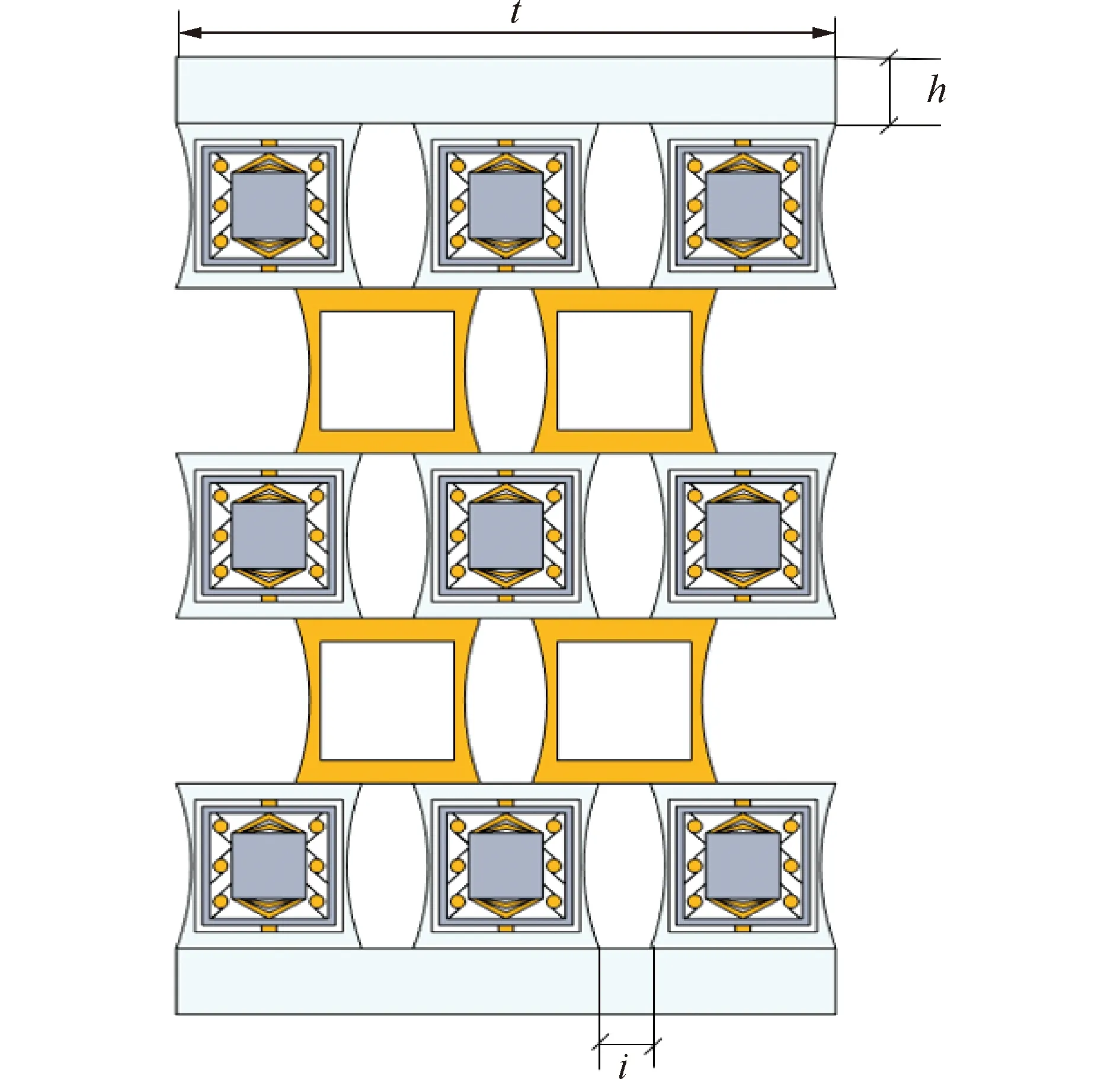
图2 整体结构示意Fig.2 Overall structure diagram

2 计算公式及计算方法

本文开展类手性拉胀型声学超结构的隔声性能研究主要集中在平面波垂直入射时的反射和透射情况进行讨论。由传统平面波入射方程可表述为：

p=paej(ωt-kxcos α-kycos β-kzcos χ)

(1)

式中α、β、χ为波阵面法线与x、y、z3个坐标轴之间的夹角，而对于只考虑平面波垂直入射的情况，式(1)也可表述为：

p=paej(ωt-kx)

(2)

如果一系列声压为p=piaej(ωt-kx)的平面声波从媒质Ⅰ垂直入射到分界面上，由于分界面两边的特性阻抗不一样，一般就会有一部分声波反射回去，另一部分透射到媒质Ⅱ中，而从媒质Ⅱ到媒质Ⅲ依然遵照此规律。

如果只有2层媒质，则媒质Ⅰ、Ⅱ中声压分别可表述为：

p1=pi+pr=piaej(ωt-k1x)+praej(ωt+k1x)

p2=pt=ptaej(ωt-k2x)

(3)

式中：pi、pr、pt分别代表平面波入射声压、反射声压和透射声压；k代表波数。

在计算隔声量即传输损失曲线时，考虑到入射声束和折射声束的面积不同，一般采用平均声能量分析透射系数，形式如图3。可表述为：

(4)

式中Ii、It分别为入射声强和透射声强;Si、St分别表示入射声束和透射声束的面积。

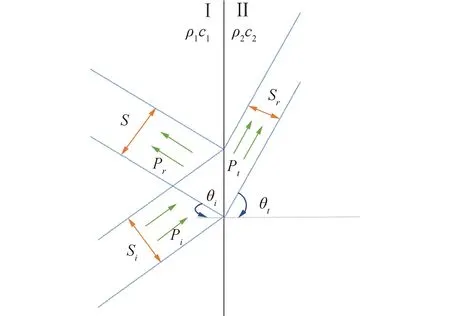
图3 透射情况示意Fig.3 Diagram of transmission

当平面波垂直入射时，Si、St的值大小相等，形式如图4所示，透射系数可直接用声强来表示，其表达式为：

(5)

传输损失的表达式为：

(6)

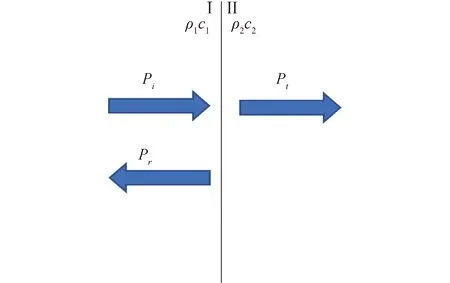
图4 垂直入射示意Fig.4 Vertical incidence diagram

本文采用有限元分析软件COMSOL Multiphysics 求解结构的传输损失曲线，为节省计算时间将模型简化为二维模型。采用多物理场耦合的方式在模型的上侧和下侧设置空气域作为入射声场和透射声场，且两侧设置完美匹配层作为无反射边界条件。在结构部分设置空气域，让结构处于空气之中，并在结构与空气接触面设置耦合边界条件。由于结构受到平面波的作用，则在结构上侧的域中设置背景压力场，背景压力场的表达式依照平面波公式设置，并将入射角度调为垂直入射。

3 模拟仿真对比

为了证明本文中仿真方法的准确性，将用本文中仿真方法模拟出的结果与其他文献中的仿真结果进行对比。在文献[32]中，作者通过将二维三组元与二维二组元声子晶体进行排列，制成声子晶体单胞以5×5的形式排列而成的结构，这里分别例举组元排列方式为32323和23232的结构形式，文中使用NASTRAN和SYSNOISE联合建立新型材料模型，其仿真结果如图5、图6所示。

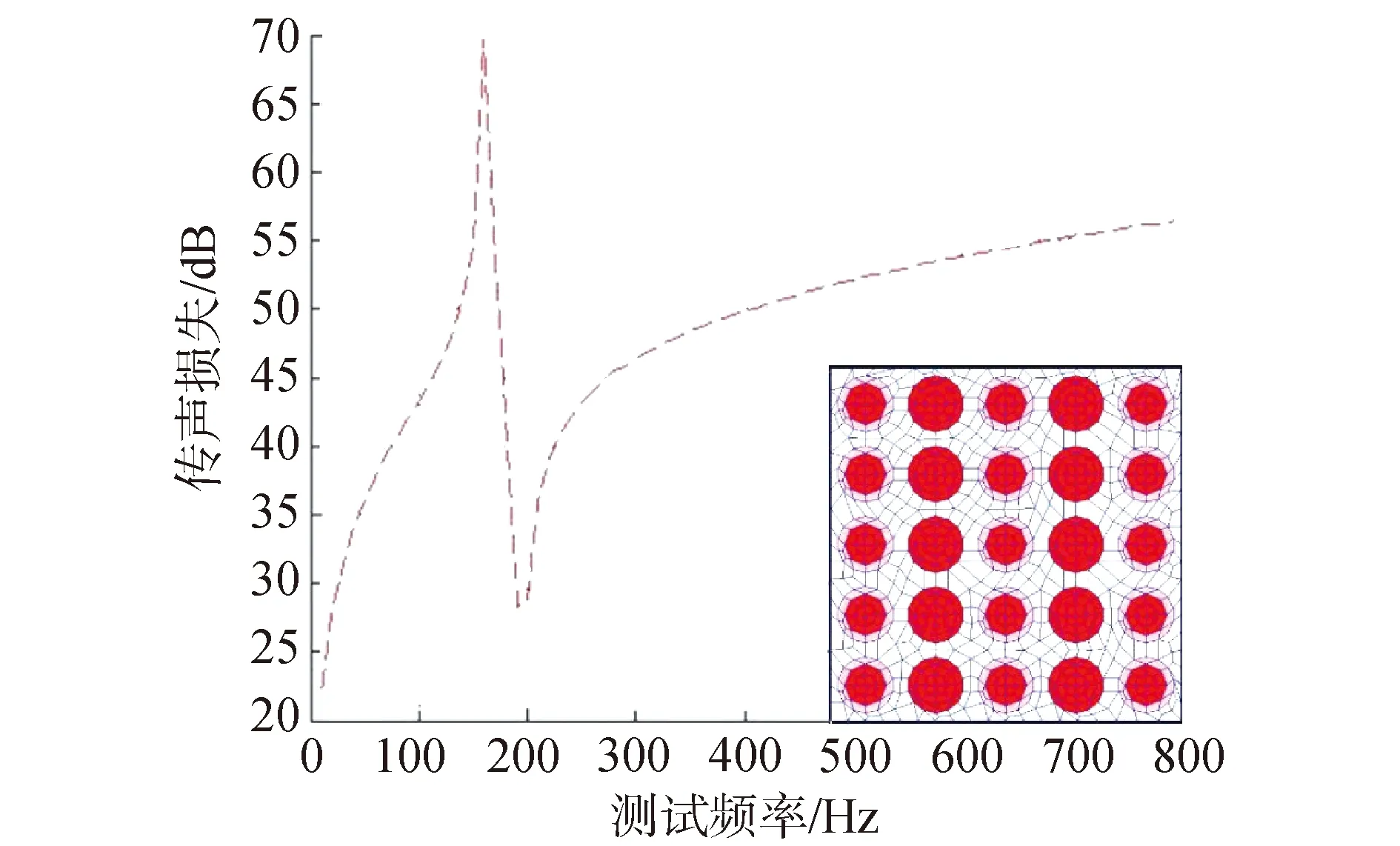
图5 23232组元形式传声损失结果[32]Fig.5 23232 Sound loss result of modular form[32]

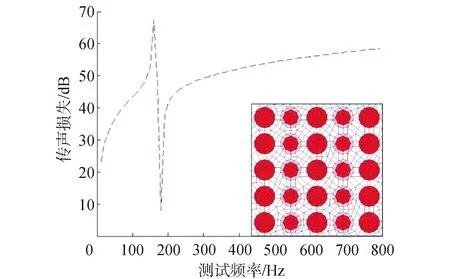
图6 32323组元形式传声损失结果[32]Fig.6 32323 Sound loss result of modular form[32]

按照本文的仿真方式，使用COMSOL 建模，并对结构两侧施加入射声场和透射声场，最终得到的仿真结果如图7所示。

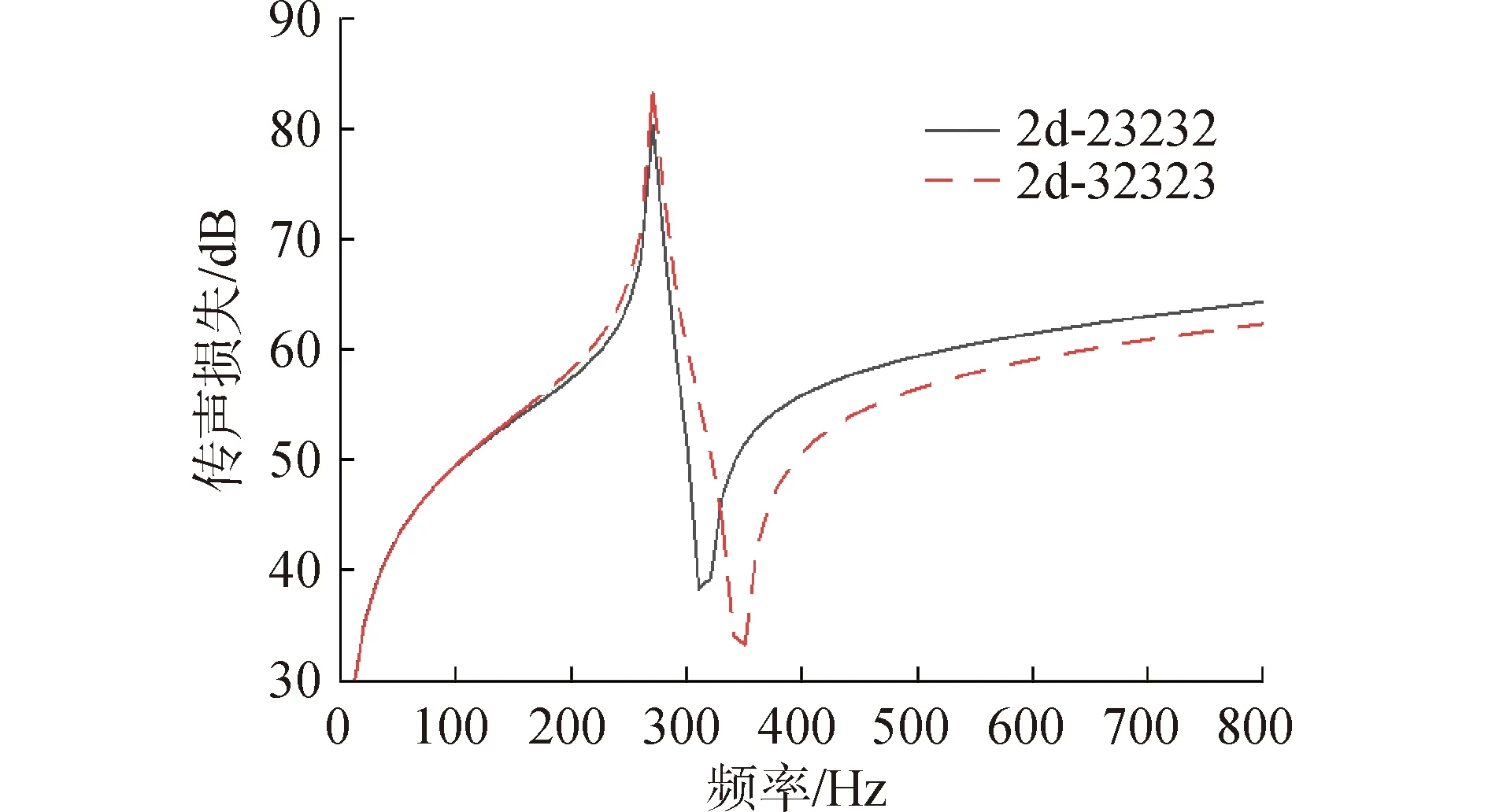
图7 COMSOL仿真对比Fig.7 COMSOL simulation comparison diagram

由仿真结果对比可知，使用COMSOL有限元分析软件的传声损失趋势与文献[32]中一致，隔声峰值比文献中略高，产生峰值的频率也比文中略高。产生误差的原因主要是由于使用的软件、算法和边界条件等因素存在差异造成的。为了进一步确认仿真的准确性，用本文的仿真方法所得到的结果与文献[33]中的带隙分析结果进行对比，确认隔声峰值、谷值与频率对应的准确性。在多重开孔式声子晶体的隔声特性研究[33]中，提出了一种局域共振型声子晶体单胞进行周期性排列后，通过引入Bloch波矢κ，使其沿不可约布里渊区的边界按一定路径进行扫描得到的带隙结果，如图8所示。

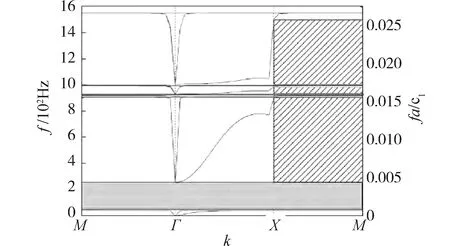
图8 多重开孔声子晶体带隙图[33]Fig.8 Band gap diagram of multihole phononic crystals[33]

按照本文的仿真方法进行模拟得到的传声损失结果如图9所示。

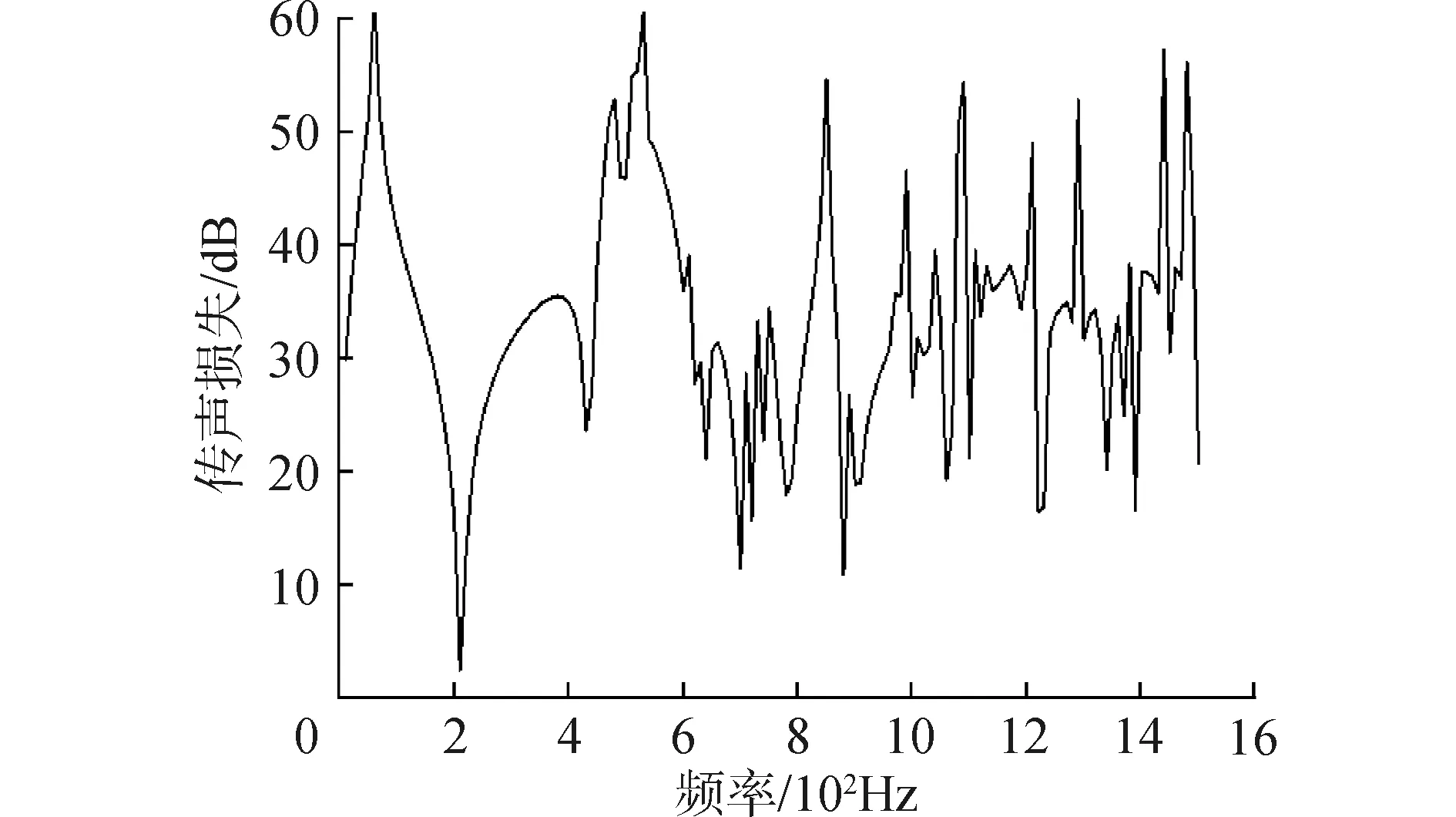
图9 多重开孔声子晶体传声损失Fig.9 Sound transmission loss in multihole phononic crystals

可以观察到，结构在0～200 Hz频段内存在一条较宽的完全带隙，可以与传声损失曲线中0～200 Hz内的隔声峰频段相对应。同时，文献中也在900～1 000 Hz存在2条较窄的完全带隙，也可与传声损失中该频段内隔声峰对应良好。

由以上2篇文献的对比结果可知，本文中的仿真方法与文献中的结果吻合良好，证明了本文仿真方法的准确性。

4 结果与讨论

4.1 声子晶体单胞结构形式改变对隔声量的影响

在结构设计过程中，考虑到局域共振型声子晶体能够在低频产生较强的隔音效果，最初只是将组元型声子晶体进行错层排列，使整体结构更加轻质，突破了质量作用定律对传统结构隔音效果的局限作用，使其在低频段具有更好的隔声能力。首先是对二组元声子晶体和三组元声子晶体进行排列，结构及传声损失曲线如图10所示。

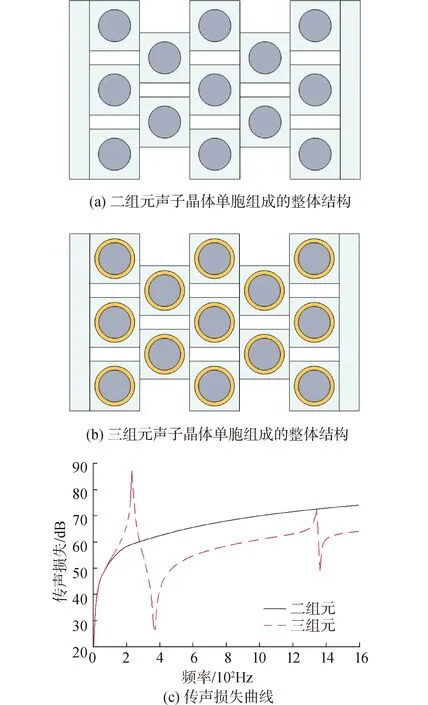
图10 结构及传声损失曲线Fig.10 Structure and sound loss curve

图中二组元结构单胞基体为玻璃，散射体为钢，三组元结构在基体和散射体之间添加了一层软橡胶包覆层，以此来充当弹簧结构，形成了弹簧—振子体系，使结构具有局域共振性能。由曲线可以看出三组元单胞结构在200 Hz附近形成了一个隔声峰，这也是局域共振型声子晶体的一种表现形式。

以上结构在低频虽然能做到具有较好的隔声性能，但是这种简单的结构堆叠方式不能承受太大的力，在一定的荷载条件下结构有可能发生变形而降低其本身的隔声性能。此时，如果将结构单胞两侧设计成弧形，使结构具有一定的拉胀性能，即使在较大力的条件下，结构也会预先向两侧变形，并不会破坏其本身的局域共振特性，其结构及传声损失曲线如图11所示。

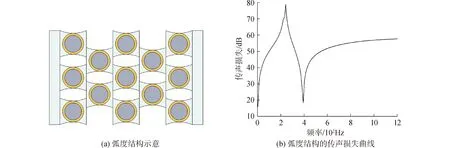
图11 弧度结构及传声损失曲线Fig.11 Radian structure and transmission loss curve

由于二组元声子晶体单胞组成的结构没有构成弹簧—振子体系，虽然在较高频段内具有更好的隔声性能，但是在所重点关注的低频段内隔声效果较差，所以研究还是以带有软橡胶包覆层的三组元结构为主，由图11可见这种边界设置弧度的结构形式既能够在一定程度上满足了整体结构的力学性能，使结构不会因发生变形而大幅度降低隔声效果，而且还基本保障了结构原有的隔音能力。

但上述结构所表现出来的问题依然很明显，那就是结构在低频隔声峰的频带宽度较窄，解决这种问题的方式有2种：1)增加隔声峰的个数，使结构在低频产生多个隔声峰，总体上提升结构的低频隔声性能；2)拓宽结构在低频的隔声峰带宽，虽然峰值只有一个，但是带宽的增加可以一定程度上增强低频段的平均隔声量。

受到文献[34]的启发，基于局域共振型声子晶体小尺寸控制大波长的特点，设计一种由复合谐振局域共振型声子晶体单胞构成的结构，其中采用多组弹簧-振子结构，希望能够在低频段形成多组隔声峰，以提升结构的低频隔声性能。最终优化的声子晶体单胞结构如图1所示，其中包覆层1中采用类手性结构，既减轻了结构自重，又起到了弹簧的作用，使整体单胞结构依然保持局域共振的特性。包覆层2中为了使结构两侧设置弧度边界不受局限，不采用叠合梁的形式，以矩形小橡胶块替代，使整体结构具有更优异的拉胀性能。同时，为了使结构在受荷载条件下能够更好地向两侧变形，在结构的2层、4层不设置声子晶体单胞，而是优化为带有弧度的正方形橡胶框架。这样处理去除了较硬的散射体和基体材料，也能使结构更加轻质。其材料仍是基体采用玻璃，散射体采用钢材，包覆层采用软橡胶。设计好的结构如图2所示，其传声损失曲线及最大峰值频率位移图如图12所示。

由传声损失曲线可以看出，结构在中低频范围内出现了很多隔声峰，且隔声峰和隔声谷的值都较单纯三组元型声子晶体单胞排列的结构高很多，平均隔声性能提升了大约30%。同时，从结构位移图中可以发现，预留在2层的正方形框架位移较大，且位移多集中于框架中部，可见框架在压力作用下会向两侧发生变形，中部主要受到拉力作用。此时是上部施加压力的情况，若从下侧施加压力，那么4层的正方形橡胶框架也会起到相应的拉胀作用，从而保障结构的声学性能不受影响。在接下来的研究中，统一以此结构作为研究对象。

4.2 材料参数改变对隔声性能的影响

研究材料参数对结构隔声性能的影响，就要分别对结构中复合谐振局域共振型声子晶体单胞中的基体、包覆层、散射体材料进行变化，并认为只改变其中某一材料参数而不用真实材料进行替换，不具有实际工程的参考价值。就整体结构而言，上下面板可看作基体，2层、4层正方形橡胶框架可看作弹簧，声子晶体类比为振子，又形成弹簧-振子结构，由于上下面板与声子晶体单胞中基体作用一致，可把两者设置为相同材料，对整体结构而言可统称为基体材料。声子晶体中包覆层作用与整体结构2、4层框架作用相同，两者也可以采用相同材料，并统称为包覆层材料。此特征在后文不重复说明。

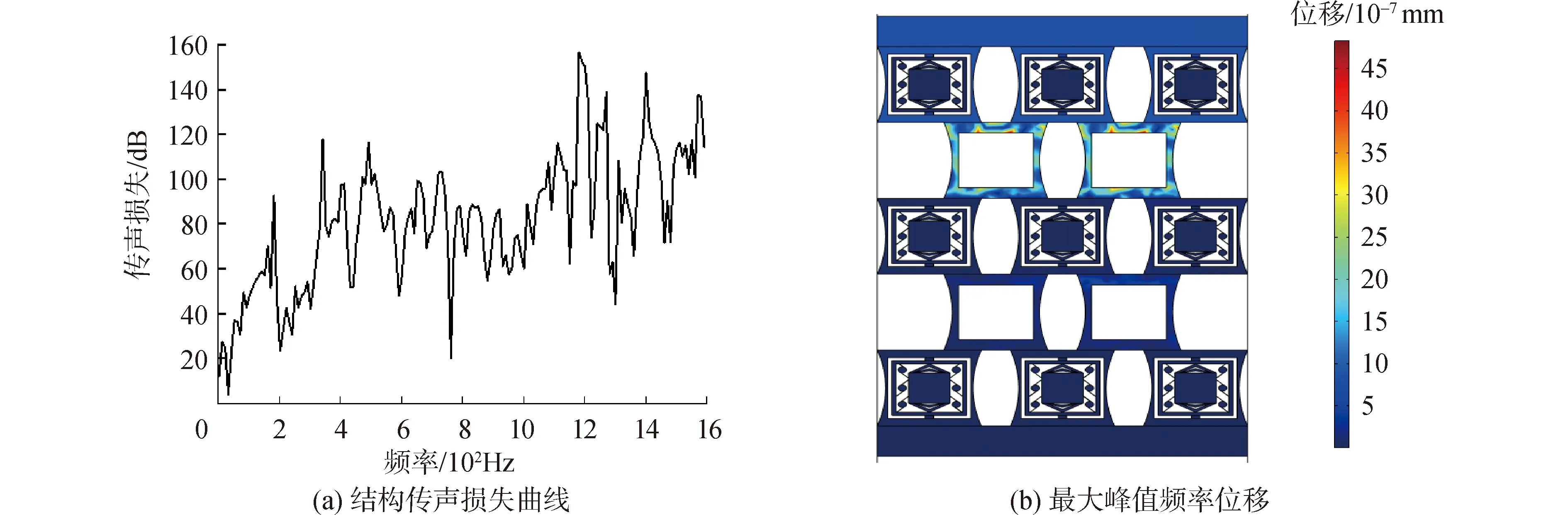
图12 结构传声损失曲线及位移Fig.12 Structure sound transmission loss curve and displacement diagram

4.2.1 基体材料改变对结构隔声性能的影响

分别以玻璃、环氧树脂、光敏树脂这几种材料作为结构基体材料，声子晶体单胞中包覆层材料仍为软橡胶，散射体材料仍为钢，且保证声子晶体单胞中除基体材料变化外，其他材料及相关参数均保持不变。改变基体材料的传声损失曲线如图13所示。

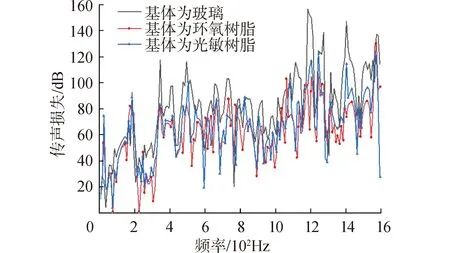
图13 不同基体材料对比曲线Fig.13 Change the matrix material contrast curve

由图中0～1 600 Hz的隔声曲线中可以发现，改变结构基体材料，对隔声峰的位置影响不大，整体曲线趋势稍有改变，变化最明显的就是隔声峰以及隔声谷的峰值和谷值。若基体为环氧树脂，其在70 Hz以及220 Hz的隔声量为0 dB，其峰值最高点是在1 560 Hz的隔声量达到了128 dB，平均隔声量在62 dB左右。若基体为光敏树脂，其在70 Hz的隔声量为4 dB，其峰值最高点是在1 240 Hz的隔声量达到了123 dB，平均隔声量在66 dB左右。若基体为玻璃，其在30 Hz的隔声量为4 dB，其峰值最高点是在1 180 Hz的隔声量达到了157 dB，平均隔声量在81 dB左右。综上所述，在散射体和包覆层材料都不变的前提下，基体材料为玻璃时结构的整体隔声性能最好，研究玻璃的密度、杨氏模量和泊松比不难发现，玻璃的密度和杨氏模量都远大于其他2种材料，很难确认究竟是两者哪一个参数对结构的隔声性能造成影响，然而对比光敏树脂和环氧树脂，两者密度和泊松比相差不大，杨氏模量光敏树脂略高，以光敏树脂为基体的结构隔声性能也更好，那么可以得出基体的杨氏模量引导着结构整体的隔声性能，材料杨氏模量越高，结构的隔声性能越好。

4.2.2 包覆层材料改变对结构隔声性能的影响

分别以软橡胶、硅橡胶和EVA橡胶作为结构的包覆层材料。同时设置基体为玻璃，散射体为钢，且其中各材料参数一定。改变包覆层材料的传声损失曲线如图14所示。

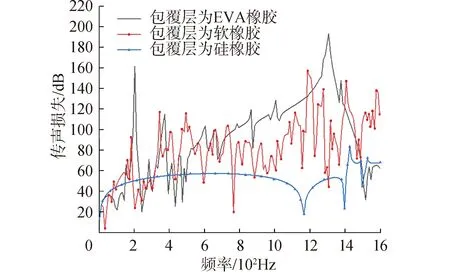
图14 不同包覆层材料对比曲线Fig.14 Change the contrast curve of cladding material

从图14中可以发现包覆层材料的改变对结构的隔声峰频段以及隔声峰值、隔声谷值都有很大的影响。当包覆层材料为EVA橡胶时，结构在500～1 500 Hz频段内产生了一个宽频隔声峰，隔声峰的峰值在1 300 Hz，峰值大小约为193 dB，结构在0～1 600 Hz的平均隔声量约为91 dB。当包覆层材料为硅橡胶时，结构在0～1 160 Hz频段范围内隔声量分布均匀，平均隔声量约为51 dB，然而结构在1 400～1500 Hz产生了一个隔声峰，峰值位置在1 420 Hz处，峰值大小约为84 dB，结构在全频带的平均隔声量约为53 dB。综上所述，在基体为玻璃，散射体为钢的条件下，包覆层材料为EVA橡胶时，结构整体的隔声效果最好。分析几种材料的参数，可以发现它们的密度相差不大，主要是杨氏模量和泊松比差异较大，将硅橡胶和软橡胶按照泊松比相近来比较杨氏模量，可以得出对于包覆层而言，杨氏模量越小的材料其整体结构的隔声性能越好。同时观察3种材料的泊松比，也可以得出想保障结构的隔声性能，包覆层材料的泊松比也不宜过大。

4.2.3 散射体材料改变对结构隔声性能的影响

分别以钢、铁、铝作为复合谐振局域共振型声子晶体散射体的材料，结构中其他部分材料不变，其中基体材料仍为玻璃，包覆层材料仍为软橡胶。改变声子晶体单胞中散射体材料的传声损失曲线如图15所示。

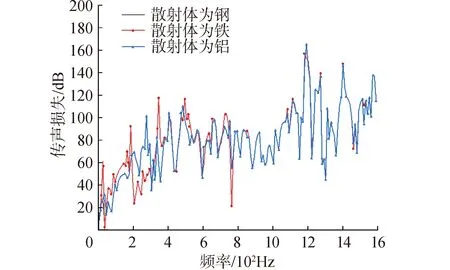
图15 不同散射体材料对比曲线Fig.15 Change the scatterer material contrast curve

从图15中可以总结出，散射体材料变化对结构隔声性能的影响较基体和包覆层小很多，若散射体为铁，其在30 Hz的隔声量为1 dB，其峰值最高点是在1 180 Hz的隔声量达到了157 dB，平均隔声量在81 dB左右。若散射体为铝，其在2 Hz的隔声量为8.6 dB，其峰值最高点是在1 190 Hz的隔声量约为165 dB，平均隔声量在81 dB左右。综上所述，比较三者的材料参数可以发现铁和钢的密度及泊松比几乎相同，只有杨氏模量相差较大，而两者曲线几乎重合，可见散射体材料杨氏模量对结构隔声性能无影响。比较铝和铁的密度和泊松比，可以得出两者泊松比近似相同，铁的密度比铝大很多。两者曲线在中高频几乎一致，在低频段散射体为铁隔声效果更好些，可见结构的隔声性能与散射体材料密度有一定关系，但其关系是非线性的。

4.3 结构布局对隔声性能的影响

在上述研究中，通过改变结构中声子晶体单胞的结构形式，列举了组元型、复合谐振局域共振型声子晶体在弧度边界条件下排列组合形成的整体结构，测试其隔声性能。接下来，要以整体结构为研究对象，讨论结构布局对整体隔声性能的影响。

改变结构布局的方式可以是调节声子晶体单胞的位置，使声子晶体排列变紧凑些或松散些，这样就可以只对上下面板和结构2层、4层的框架变形即可。当结构连接框架为边长为16 mm的正方形框架时，两声子晶体单胞间距5 mm，当结构连接框架为边长为36 mm的正方形框架时，两声子晶体单胞间距21 mm。变形后模型及隔声量对比曲线如图16所示。

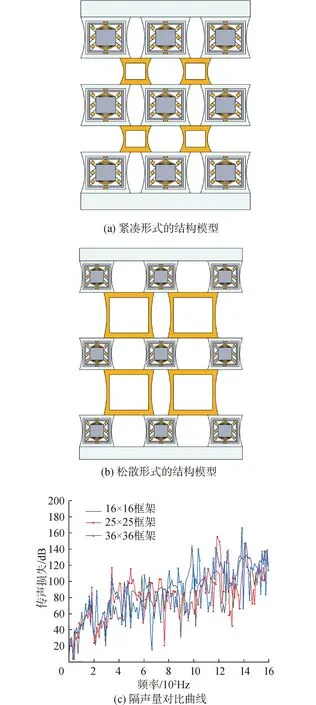
图16 不同结构布局模型及隔声量对比曲线Fig.16 Variable structure layout model and contrast curve of sound insulation

从曲线对比结果可以看出，声子晶体单胞从紧凑变松散的过程中，最大隔声峰的位置在不断向高频移动，且最大隔声峰的峰值也在不断增加。但就平均隔声效果来讲，三者的隔声性能都较为优异。

5 结论

1)将模拟结果与前人文献进行对比，验证了本文仿真方法的准确性。通过改变声子晶体单胞形式，将组元型声子晶体的局域共振特性进行复合，形成复合谐振型声子晶体，使整体结构的隔声性能提升了30%。

2)通过改变结构各部分材料得出，基体及上下面板材料杨氏模量越高，结构的隔声性能越好。包覆层及连接框架杨氏模量和泊松比都不易过大。散射体杨氏模量对结构隔声性能影响较小，但密度对隔声量有一定影响。

3)通过改变结构布局得出，声子晶体单胞从紧凑变松散的过程中，最大隔声峰的位置在不断向高频移动，且最大隔声峰的峰值也在不断增加，但整体结构的隔声性能都较优异。