礼让行人条件下右转保护型相位设置阈值研究
张智勇,黄鑫灿,邵 越
(北京工业大学 交通研究中心,北京100124)
0 引 言
随着居民出行需求的增加,城市道路交通组织变得更加复杂,交叉口范围内人车冲突频发,其中以右转机动车与行人的冲突尤为突出。《中华人民共和国道路交通安全法》[1]规定:“行人具有优先通行权,机动车遇行人正在通过人行横道时,应当减速避让”。我国各地开展了礼让行人专项整治活动, 出台了具体的礼让行人细则。但是实地调研发现,许可型相位下右转机动车避让概率并不理想。机动车驾驶员不遵守避让规则、与行人相互争夺路权的现象时有发生。这种现象既影响了交叉口运行效率又增大了安全隐患。右转保护型相位的设置可将人车冲突从时间上分离,提升交叉口安全性,但右转保护型相位的设置必然会降低交叉口运行效率。因此兼顾交叉口的安全性与运行效率来研究右转保护型相位的设置条件具有重要意义。
国内外学者对人车交互行为和右转保护型相位的设置均有一定研究。N.D.VINEY等[2]在行人具有优先通行权条件下,基于穿越间隙理论,建立了转弯车辆受行人影响下的饱和流量模型。在运行效率方面,刘泳玲[3]依据不同的相位方案分析了交叉口处人车交互行为,利用穿越间隙理论建立了人车交互影响下右转专用车道通行能力模型;张茂民等[4]建立了两种控制方案下信号控制延误和人车交互延误模型,提出了右转保护型相位的设置条件。而在安全性方面,张海波[5]使用灰色聚类法对人车冲突区域进行安全性评价,并作为右转保护型相位的设置依据。前期研究深入分析了人车交互行为对交叉口运行效率和安全性的影响,但多数研究仅考虑单一交通流的延误或通行能力,无法均衡各交通参与者的收益。
“以人为本”交通理念的发展使学者更重视过街行人的交通需求。徐建闽等[6]计算了不同穿越方式下行人与机动车的临界穿越间隙,提出了基于右转机动车和行人总延误最小的保护型相位设置条件。礼让行人交规环境下,人车交互机理也发生了变化。魏丽英等[7]依据人车交互过程中交通参与者让行决策收益构建人车冲突博弈矩阵,建立了人车冲突演化的动力学模型;虞笑晨等[8]通过VISSIM仿真分析机动车是否礼让行人、行人流量大小等不同场景下对机动车延误的影响。然而,实际中机动车的让行率未达到100%,车辆延误随避让率动态变化过程未被考虑。礼让行人法规实施后,人车运动状态发生了变化,这直接会导致信号交叉口交通模型(通行能力估计模型、延误估计模型等)发生改变[9],以往关于交通模型计算的理论与方法将有待完善。综上,笔者基于可接受间隙理论,考虑机动车避让率和双向过街行人影响,根据过街行人瞬时密度分布特性,分阶段建立信号交叉口人车交互延误估计模型。同时考虑到设置右转保护型相位对交叉口安全性能上的提升,在设置条件中加入安全调整系数,研究右转保护型相位的设置条件。
1 右转机动车与行人交互特性分析
1.1 冲突区域划分
我国多数信号交叉口未设置右转保护型相位,许可型相位下右转车辆将与平行或相交人行横道上的过街行人发生冲突。由于行人相位总是与同向机动车直行相位并行设置,所以在一个信号周期内,右转车辆不会同时与两个方向的过街行人发生冲突。冲突区域假定为右转车辆行驶轨迹与人行横道的交织区域,如图1。
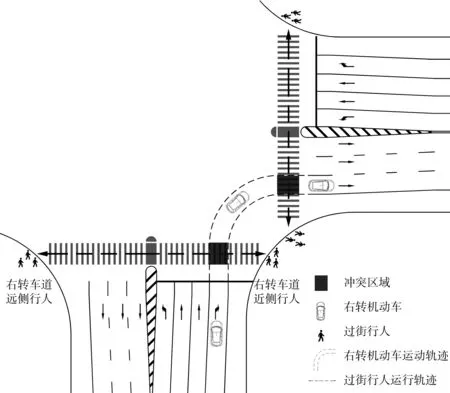
图1 信控交叉口右转机动车与行人冲突示意
1.2 过街行人的时空分布特性
礼让行人实施前后,行人和右转机动车的运动状态也发生了改变。实施前,过街行人和右转机动车等待可穿越间隙通行,实施后当右转机动车做出避让决策时行人也可通行。礼让行人实施后右转机动车与行人的运动状态如表1。

表1 礼让行人条件下右转机动车与行人运动状态
依据行人的动态过街行为可得出直行相位期间行人密度分布的瞬时特性[10]。以交叉口一处人行横道为例,做出行人直行相位期间不同时刻的行人瞬时密度分布热度图(图2)。
由图2可以得出在行人直行相位不同时期双向过街行人的分布特性。因此可将人车交互过程划分为5个阶段,进而建立人车相互干扰的延误估计模型。
2 考虑避让率的右转机动车与行人冲突延误估计模型
2.1 基本假设
2.1.1 假设1
假设右转机动车和行人到达服从泊松分布,则其车头时距服从负指数分布。设平均到达率为λ,veh/s,则车头时距h的概率密度函数为[11]:
(1)
车头时距h大于等于临界穿越间隙τ的概率为:
P(h≥τ)=e-λτ
(2)
2.1.2 假设2
同时假设右转机动车避让决策引起的避让延误不会影响车流的车头时距分布,这也是《美国高速公路通行能力手册》[12](HCM2000)在计算由避让行为导致的行人延误减少时的假设。
2.1.3 假设3
实际上双向过街行人的时空位置受同向进口和相交进口右转车流的影响。为便于分析右转保护型相位设置阈值,假定双向过街行人分担率相同,且过街时空分布特性相似。
2.2 穿越间隙分析
右转机动车需要穿越的距离包括冲突区域宽度和车身长度两部分,则右转机动车穿越行人的临界穿越间隙τp为[6]:
(3)
式中:Lc为车身长度,m;Wcl为冲突区域长度,m;a1为右转机动车加速离开的加速度,m/s2;Wcw为冲突区域宽度,m;Vp为行人过街速度,m/s。
行人穿越右转车辆的临界穿越间隙τv为:
(4)
式中:tR为行人的反应和判断时间,s;tp为右转车通过冲突区域的时间,s
2.3 模型建立
2.3.1 行人干扰造成的右转机动车延误
1)第一阶段:行人绿灯相位启动初期,红灯期间累积到达的行人从人行横道到达冲突区。
行人绿灯启亮初期,在行人群从等待区开始释放至冲突区的时间内到达的右转机动车若不采取避让行为可以无延误直接通过。若右转机动车做出避让决策,需等待右转车道近侧行人群通过冲突区域才可选择通过,此时行人分布特性如图2(a)。笔者假定车辆避让率为分段函数,如式(5):
(5)
式中:M为小于1的常数。
第一阶段时间ta(行人从人行横道处到达冲突区域所需时间)如式(6):
(6)
式中:Lp为人行道等待区到冲突区域的距离,m。
红灯期间内到达的行人群消散时间tb为:
(7)
式中:λQ为过街行人消散速率,ped/s;Tr为过街行人红灯时长,s。
行人群到达并通过冲突区域时间tc为:
(8)
式中:np为饱和流量下可并排行走的最大行人数;L′p为前后两排过街行人之间的步行间距,m。
(9)
(10)
式中:Vc为右转机动车初始速度,km/h;a2为右转机动车停车避让加速度,m/s2;S为决策区域至冲突区域的距离,m。
(11)
式中:λv为右转机动车到达率,veh/s;
2)第二阶段:右转车道近侧红灯期间累计的行人穿越冲突区域。
由于右转车道近侧行人数量较大,在冲突区域较为强势,该阶段到达的右转车辆需停车等待至行人群到达并穿越冲突区域才可选择通过。此时行人时空分布特性如图2(b)。右转机动车的延误包括等待时间以及加减速损失时间。
(12)
(13)
3)第三阶段:红灯期间累计的行人离开冲突区域,后续过街行人随机到达。
右转车道近侧行人群离开冲突区域后直到对向行人群到达冲突区域前,这一期间到达的右转车辆和前两个阶段受行人群阻滞而停车避让的车辆,等待后续过街行人出现可穿越间隙时,进行决策离开冲突区域。该阶段行人分布特性如图2(c)。
经典穿越间隙理论认为,只有当主路交通流车头时距h≥τ时次路交通流才可穿越。因此主路上任意一个间隔被接受的概率如式(2)。
拒绝的概率为:
P(h<τ)=1-e-λτ
(14)
则次路车辆等待的间隔数为k的概率为[11]:
P(x=k)=(1-e-λτ)ke-λτ
(15)
由于穿越间隙理论未考虑机动车主动礼让行人因素,为使模型适用于礼让行人交规下人车交互过程分析,笔者对穿越间隙模型进行改进。人车交互过程中存在3种事件:①行人过街时距小于临界穿越间隙,右转车辆无法通过;②行人过街时距大于临界穿越间隙,但右转车辆选择让行;③行人过街时距大于临界穿越间隙,右转车辆选择不让行通过。这3种事件发生的概率互斥且和为1,则发生其中一个事件x次的概率服从三项分布。笔者将右转机动车避让率作为模型参数以改进临界穿越间隙模型。
通过概率论与数理统计相关理论可得,右转车辆穿越行人前等待的间隔数为k的概率为:
e-λpτp)k(e-λpτpM)0e-λpτp(1-M)
(16)
右转机动车等待行人的平均数目如式(17):
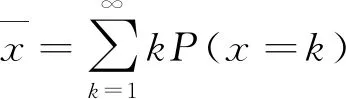
(17)
当行人群的过街时距小于临界穿越间隙时,右转车辆不能穿越,此时右转车辆的平均等待时间为:
(18)
当行人群的过街时距大于临界穿越间隙,但右转车辆驾驶员做出避让决策,此时右转车辆的平均等待时间如式(19):
(19)
则右转机动车等待一个行人的平均时间为:
(20)
因此每辆右转机动车的车均延误时间为:
(21)
该阶段持续时间为右转车道近侧行人通过冲突区域的时刻至远侧行人到达冲突区域的时间,依据假设3可得该阶段持续时间td为:
(22)
式中:L为进口道右转车道近侧冲突区域与远侧冲突区域间的距离,m。
该阶段受行人过街影响的右转车辆总延误为:
(23)
对向行人到达冲突区域前,若停车线后的右转机动车未能完全消散,则第三阶段结束时剩余车辆数为:
(24)
4)第四阶段:红灯期间右转车道远侧累积的行人群到达并穿越冲突区域。
该阶段内到达的右转机动车,受过街集群行人阻滞,需停车等待至行人群到达并穿越冲突区域。该阶段到达的右转机动车的车均延误与第二阶段类似,这时行人分布特性如图2(d)。
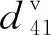
(25)
(26)
5)第五阶段:双向过街行人随机到达,右转机动车等待可穿越间隙通过。
当红灯期间累计的双向过街行人都通过冲突区域后,后续行人随机到达,该阶段行人分布特性如图2(e)。这时只有当双向过街行人车头时距均大于临界穿越间隙,并且机动车需做出穿越决策才可通行,其概率为:
P(h1>τp,h2>τp)(1-M)
(27)
则右转车辆等待第k个间隔才可穿越的概率为:
h2≥τp)(1-M)
(28)
此时右转车流不能穿越行人群的情形分为以下3种可能。
当单向行人群的过街时距小于临界穿越间隙时,右转车辆无法穿越,此时平均等待时间如式(29):
(29)
当单向行人群的过街时距大于临界穿越间隙时,右转车辆仍无法穿越,此时平均等待时间如式(30):
(30)
当双向行人群的过街时距均大于临界穿越间隙但右转车辆做出避让决策,此时平均等待时间如式(31):
(31)
因此可得该情形下右转车辆等待一个行人的平均等待时间为:
(32)
此阶段右转车辆车均延误如式(33):
(33)
该阶段持续时间如式(34):
te=(Tg-ta-2tc-td)
(34)
式中:Tg为过街行人绿灯时长。
该阶段内受行人过街影响的右转机动车总延误为:
(35)
若受过街行人干扰,在行人直行相位结束时未能完全消散而滞留在停止线后的右转机动车数为:
(36)
受到行人干扰影响的滞留在停止线后的右转机动车在下一相位以饱和流率消散,这时右转机动车总延误时间为:
(37)
式中:λdis为右转机动车消散速率,veh/s。
则一个信号周期内受过街行人干扰造成的右转车辆总延误Dv为:
(38)
2.3.2 右转机动车干扰造成的行人延误
1)第一阶段:行人绿灯启亮初期,红灯期间累积的行人从人行横道到达冲突区域,并截断右转车流。
信号启动初期,行人群等待右转车流中出现可穿越间隙或右转车辆做出避让决策才可截断右转车流通行。则行人等待至右转车流第k个间隙才可穿越的概率为:
P(x=k)=[(1-e-λvτv)(1-M)]k[e-λvτv+
M(1-e-λvτv)]
(39)
行人等待右转机动车的平均数目如式(40):
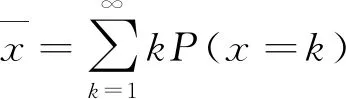
(40)
行人等待一辆右转机动车的平均时间如式(41):
(41)
该阶段内受右转机动车影响的过街行人总延误时间如式(42):
(42)
2)第二阶段:右转车道近侧红灯期间累计的行人穿越冲突区域。
当红灯期间累计的行人群穿越冲突区域时,受集群行人阻滞影响,右转车辆难以穿越且只可停车等待,行人可不受干扰通过,此时行人过街无延误。
3)第三阶段:红灯期间累计的行人群离开冲突区域,后续过街行人随机到达。
当红灯期间累积的行人通过冲突区域后直至对向行人到达冲突区域时,此时后续过街行人随机到达,行人寻求机动车可穿越间隙或驾驶员做出避让决策才可通行,此时行人受右转机动车干扰造成的过街延误与第一阶段相同。
该阶段过街行人总延误如式(43):
(43)
4)第四阶段:右转车道远侧红灯期间累计的行人穿越冲突区域。
当右转车道远侧过街行人到达并穿越冲突区域时,远侧过街行人阻滞右转车辆,右转车道近侧行人也可不受干扰直接通过,此时行人过街无延误。
5)第五阶段:远侧过街行人离开冲突区域后,双向过街行人随机到达。
当右转车道远侧过街行人通过冲突区域时,双向过街行人随机到达,行人寻找右转车辆可穿越间隙或右转车辆做出避让决策才可通过。此时行人过街延误与第一、三阶段相同。
该阶段内受右转车辆影响的过街行人总延误为:
(44)
则一个信号周期内受到该进口右转车辆干扰造成的双向过街行人总延误为:
(45)
2.3.3 设置右转保护型相位后右转机动车信控延误
计算设置右转保护型相位后的信控延误采用HCM2000中的延误估计模型[12]。每辆右转机动车的信控延误按式(46)计算:
dS=d1+d2+d3
(46)
其中,均匀控制延误d1为:
(47)
式中:C为信号周期时长,s;g为有效绿灯时间,s;X为饱和度。
增量延误d2为:
(48)
式中:T为分析时段长度,h;K为增量延误参数;I为交叉口上游修正参数;c为车道通行能力,veh/h;
假定分析时段末无排队车辆,初始排队延误d3=0,则一个信号周期内因设置右转保护型相位引起的通过冲突区域车辆信控总延误为:
DS=λv(Tg1+Tr1)dS
(49)
2.4 灵敏度分析
为了标定模型各项参数,分析模型中参数的灵敏度。笔者于2021年4月5日(星期一)对北京市顺义区顺白路—顺于路交叉口进行实地调查,数据采集时段为晚高峰时段(17:00—19:00),观测时段内天气良好且无重大活动、事故发生。调查内容包括交叉口静态特征、右转机动车让行率等,如表2。
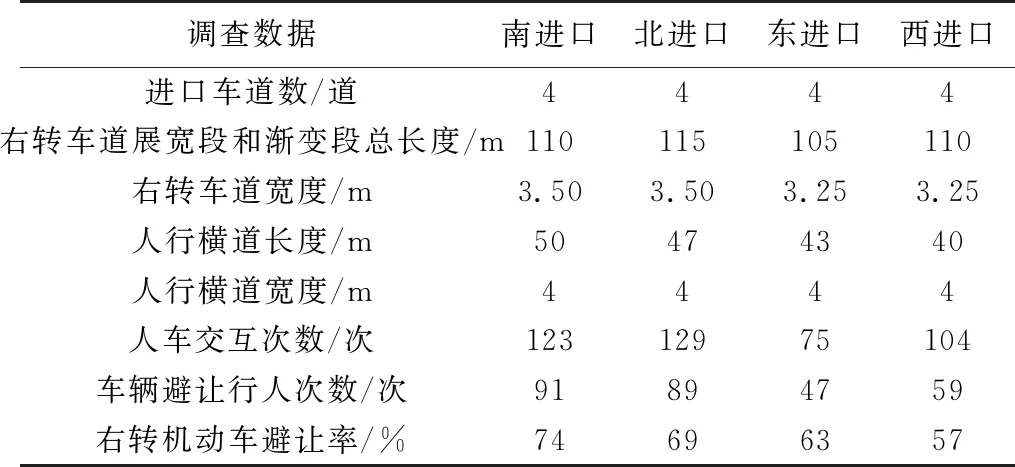
表2 交叉口几何条件及人车交互数据
该交叉口为主-主相交交叉口,信号配时方案为相位一南北直行40 s,相位二南北左转30 s,相位三东西直行50 s,相位四东西左转40 s。每个相位间有3 s的黄灯时间与3 s的全红时间。在HCM2000中,记录了一些关于不同交叉口的避让率现场观测结果,相应的避让率范围为0.47~0.90[13]。在本次灵敏度分析中,以交叉口南进口道为例分析了包括交叉口实际避让率和多种不同避让率取值条件下冲突区域人车交互总延误在不同交通量场景下的变化情况,如图3。
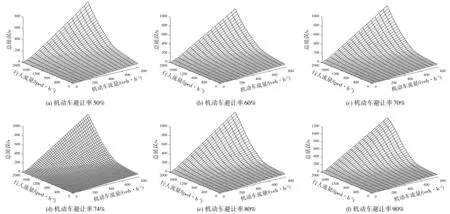
图3 不同避让率条件下冲突区域人车交互总延误
由图3可知:
1)避让率相同时,随着交通量的增加,人车交互总延误随之增加。这是因为流量越大,车头时距大于可穿越间隙的概率越低,导致机动车与行人平均等待间隔数和平均等待时间增加。延误对高密度交通流的流量变化更敏感,高流量条件下的人车交互延误的增速比低流量情况下更快。
2)随着机动车避让率的增加,右转机动车与行人的总延误随之增加。这是因为随着机动车避让程度的提升,行人过街受到的干扰延误减小,但右转机动车由此产生的避让延误增加,且机动车的避让延误增速大于行人受到的干扰延误增速。
3 右转保护型相位设置条件
3.1 右转保护型相位设置形式
右转保护型相位通常在原有信号配时的基础上作为左转相位的跟随相位设置,绿灯时长等于左转相位的绿灯时间,即一次信号周期中右转车辆可获得两次通行权。以典型四相位信号控制交叉口为例,相位图如图4。
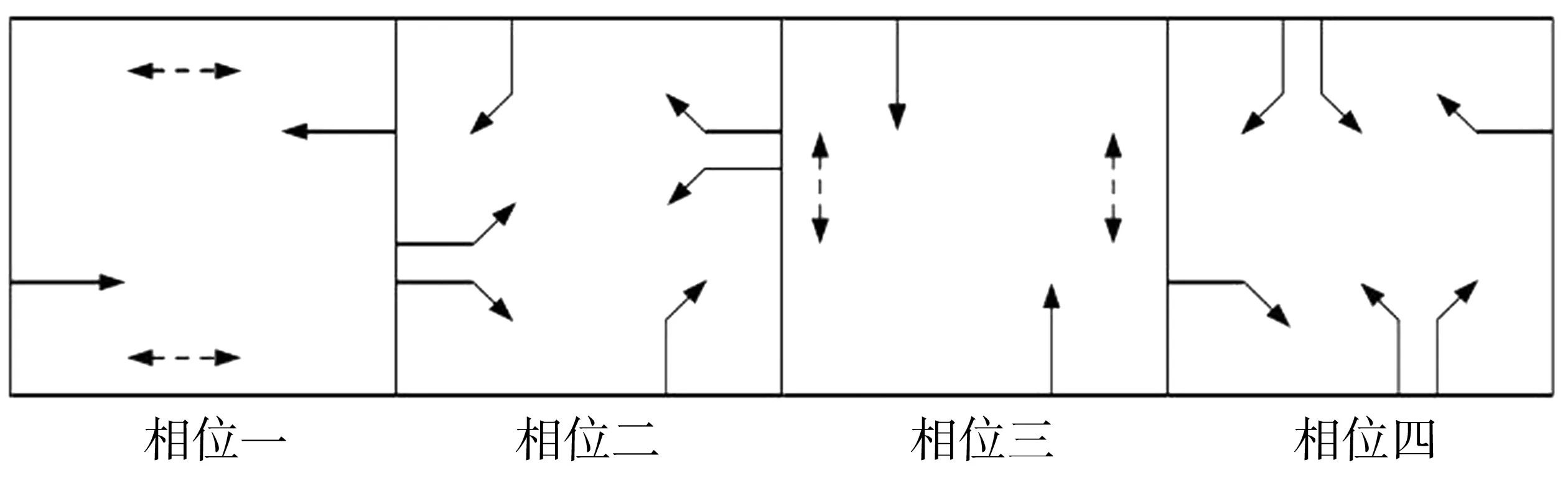
图4 右转保护型相位设置
3.2 右转保护型相位设置条件分析
3.2.1 冲突区域人车交互总延误
右转保护型相位的设置消除了右转机动车与过街行人冲突区域,故保护型相位设置后的延误由冲突区域人车交互总延误变为右转机动车信控延误。右转保护型相位的设置并不影响双向过街行人阻滞延误和行人信控延误,故不将其作为影响变量。同时右转保护型相位的设置为交叉口带来了安全性能的提升,故右转保护型相位的设置应允许延误的小幅提升。除此之外,还应考虑保护型相位设置后对交叉口其余交通流的影响。
3.2.2 右转车流与相交道路直行车流合流延误
受交叉口设计和驾驶员遵章性等影响,右转车流强行阻断相交道路直行车流,与直行机动车抢道行为时有发生,引起了两种交通流的合流延误,如图5。右转保护型相位的设置将两种交通流从时间上进行分离,消除了合流延误,因此交叉口直右合流延误也应作为设置右转保护型相位的考虑因素。
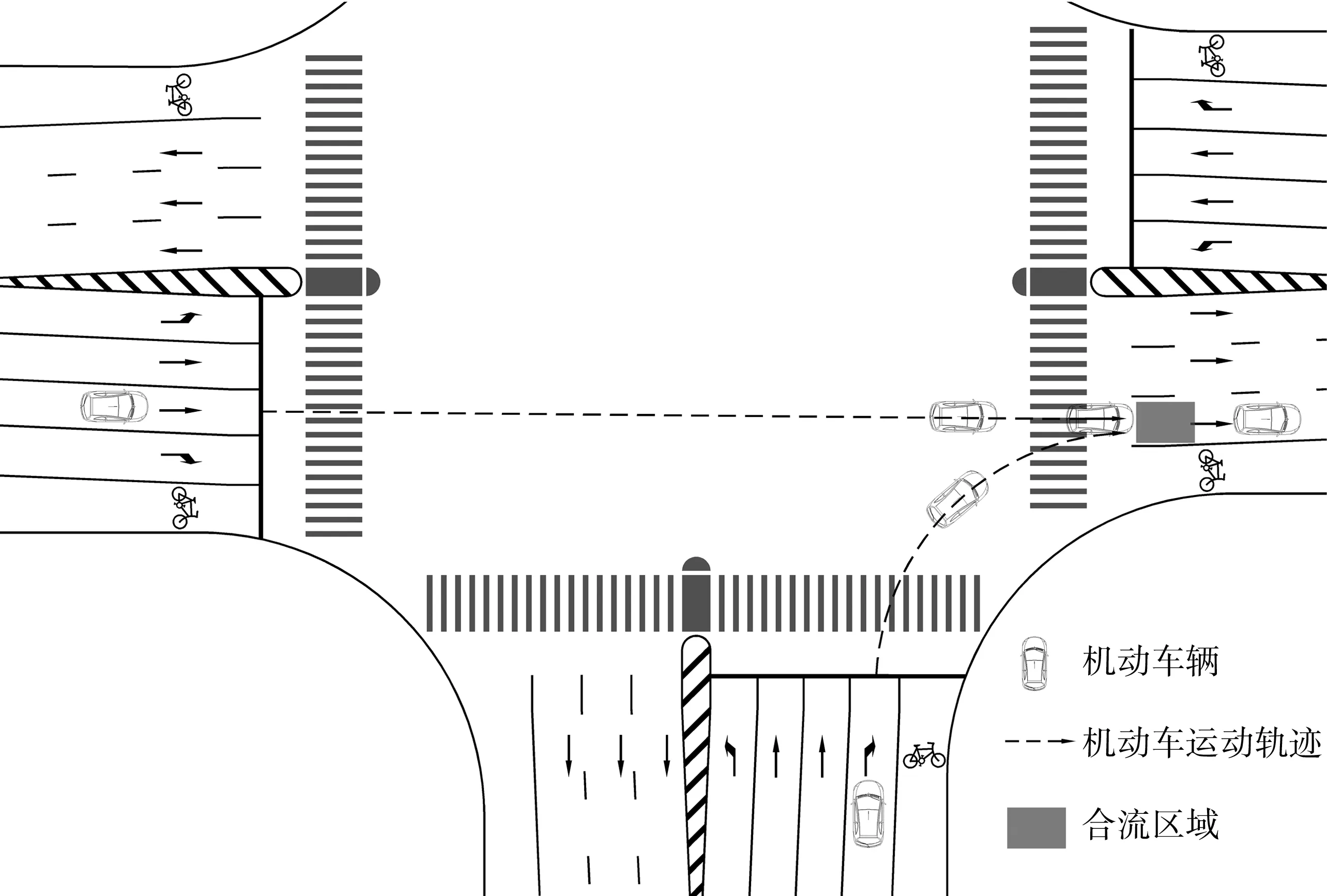
图5 直行与右转车辆合流冲突示意
尹雨洁[14]基于Admas模型构建了右转车流车头时距服从移位负指数分布、直行车流车头时距服从M3分布的合流延误计算模型。借鉴这一研究工作可以得到两种车流车头时距均服从负指数分布的合流延误计算模型。
右转机动车合流延误计算模型如式(50):
(50)
式中:λr为右转车流到达率,veh/s;Tsg为直行绿灯时间,s;λs为直行车流到达率,veh/s;τs为直行车流临界穿越间隙,s;γ、ε为常量,当右转车流随机到达时,γ=0。
相交道路直行机动车合流延误计算模型:
(51)
式中:p为交通强度或利用系数;tv为直行机动车拥有绝对通行权时临界间隙,取tv=5 s;tf为右转机动车以车队形式连续穿越直行机动车流的跟驰车头时距,一般为3~5 s。
3.2.3 右转车道排队车辆溢出影响
信号交叉口设置展宽段是普遍的渠化措施,设置展宽段后右转机动车和同向直行机动车存在分流点,若右转车道展宽段和渐变段长度不足则会导致右转保护型相位设置后右转车辆排队溢出从而造成两种交通流的相互阻挡,如图6。

图6 右转排队车辆溢出影响示意
右转保护型相位的设置应考虑右转车流排队溢出现象,即右转车流最大排队长度不应大于右转展宽段和渐变段总长度。HCM2000中给出了计算排队长度的模型[12],如式(52):
Q=Q1+Q2
(52)
式中:Q1为排队长度第一项,辆;Q2为排队长度第二项,辆。
(53)
式中:FL为右转车道流量,veh/h;XL为流率与通行能力之比。
(54)
式中:kB为第二项修正系数;QbL为车道初始排队长度,辆。
综上所述,可得出右转保护型相位的设置条件如式(55),且设置后右转车道排队车辆不应溢出展宽段。
DS≤δ(Dv+Dp+DMS+DMR)
(55)
式中:δ为安全调整系数,δ≥1。考虑到设置右转保护型相位带来的安全性能的提升,应允许延误的小幅提升。
3.3 右转保护型相位设置阈值分析
通过数值分析发现,当右转机动车流过饱和时,设置右转保护型相位引起的机动车增量延误远大于人车交互延误且会造成右转排队车辆溢出,此时再采取信号控制会造成运行效率的过多损失,不具备设置右转保护型相位的条件。调查交叉口几何结构上对称,上游进口道与下游出口道车道数量对应。为便于表示右转保护型相位设置阈值,右转车流与相交道路直行车流合流影响可以忽略。因此笔者只考虑右转车流未饱和时,不同机动车流量、双向过街行人流量、避让率取值下右转保护型相位开启阈值,数值仿真结果如图7。
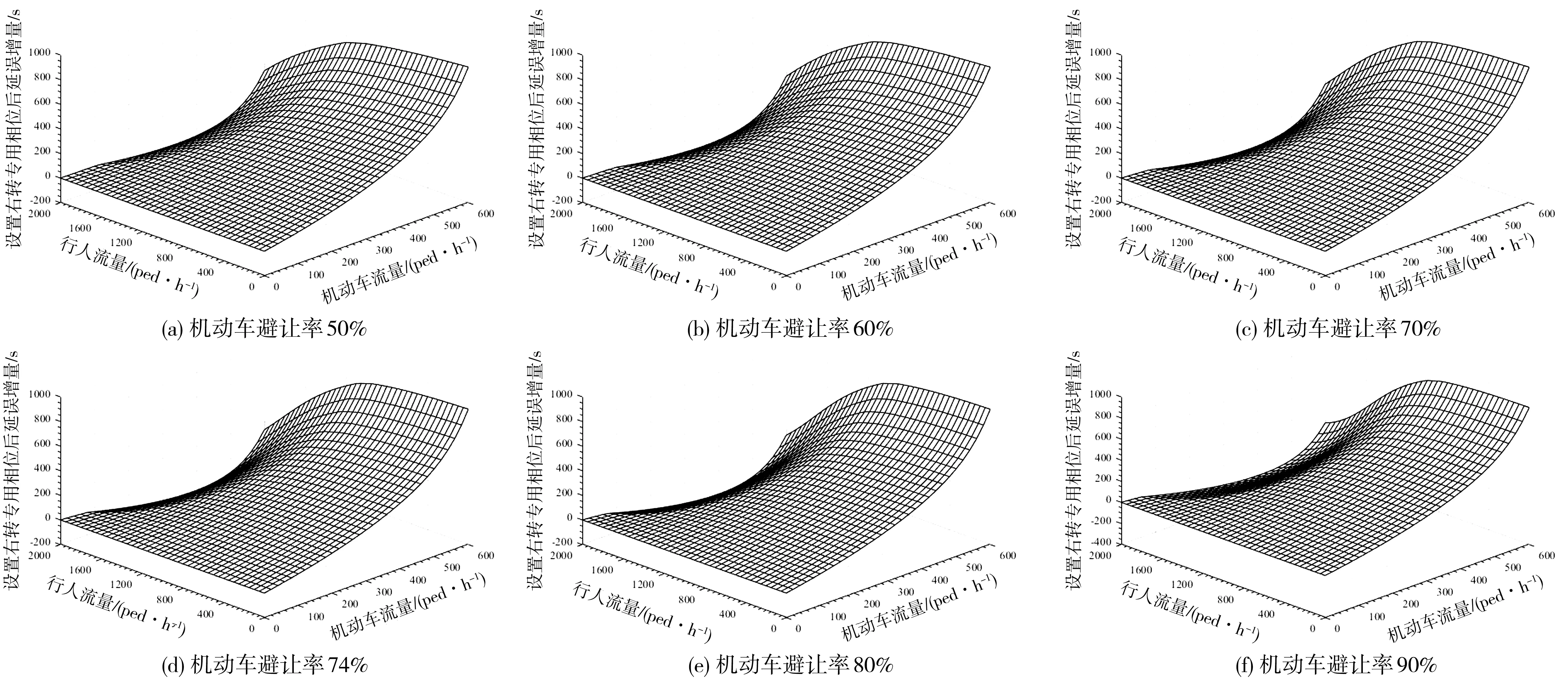
图7 不同避让率条件下设置右转保护型相位后延误增量
从图7可以得出以下结论:
1)当行人流量较少时,人车交互造成的干扰延误及设置右转保护型相位后带来安全效益的提升不足以弥补设置右转保护型相位导致的运行效率损失。行人流量越多,设置右转保护型相位后延误增量越小,更具备设置条件。当机动车流过饱和时,即使行人流量不断增加,交通参与者的总延误远小于由于信号控制带来的增量延误,此时再设置右转保护型相位是不可取的,应考虑设置行人过街天桥、增设右转车道、采取右转渠化措施等方案。
2)相同交通流量条件下,随着机动车避让率的提升,人车交互总延误越大,设置右转保护型相位后延误增量越小。
3)多数情况下当进口右转机动车流量在100~550 veh/h、双向过街行人流量达到1 700 ped/h以上时,适宜设置右转保护型相位。且随着车辆避让率的增大,设置右转保护型相位对流量要求逐渐变低,这是因为产生了更大的避让延误,此时设置右转保护型相位有助于提高交叉口运行效率和整合交叉口运行秩序。
4 结 论
笔者通过对北京市交叉口的实地调研分析了交叉口人车交互行为,基于可穿越间隙理论建立了避让率与双向过街行人影响下的人车交互总延误模型。综合考虑设置右转保护型相位前后交叉口运行效率与安全性变化,得到了右转保护型相位设置条件。
研究表明,在右转车流未饱和的情况下,右转保护型相位更加适合高避让率、高行人流量和较低车流量的交叉口。随着避让率的增高,右转保护型相位的设置对流量的需求逐渐变低。随着车流量的增长,右转保护型相位的设置对行人流量的需求呈现先降后升的趋势。笔者提出的人车交互延误模型和右转保护型相位设置条件可为相关管理部门制定交通管控、交叉口改善措施提供理论依据。
需要指出的是实际上车辆的避让行为是一个多变量参与的决策过程,车辆避让率影响因素众多,笔者只考虑了指定避让率范围内取值的情况。右转保护型相位设置条件受交叉口多因素、多股交通流的影响。笔者为直观表示设置阈值,采取交叉口进口道一个冲突区域交通参与者总收益作为决定条件,后期研究应对交叉口多股交通流流量进行设置阈值分析。在实际应用中还应将相邻交叉口的间距能否满足车辆的行驶需求(交织、加速、减速等)考虑在内,延误模型中多个交叉口间信号联动系数的修正也应被考虑在内。

