基于北极航线通航期冰情的多种船舶航速优化

闵德权，江可鉴，刘 茹

(大连海事大学 交通运输工程学院，辽宁 大连 116026)

0 引 言

随着全球气候持续变暖，北极海冰的覆盖面积逐渐缩小，北极航线的通航问题得到了更多的关注与研究。总体来看，北极航线可分成东北航道、西北航道以及穿极航线。北极航线东北航道的通航期从7月中下旬开始，在10月中下旬结束[1]。但相较传统航线，其具有航线时间和航线成本上的优势。

针对船舶的航速优化，需先对航线进行总体分析。ZHENG Binglei等[2]通过对北极航线上船舶航行的航速、干扰以及延迟等因素进行分析，建立以航线运营成本最小为目标的优化模型；关晓光等[3]在对北极航线的东北航线进行航次的收益和效率分析的基础上，建立环绕模式集装箱航线优化模型；J.H.NAM等[4]基于海冰和环境等数据，建立交互式的仿真系统，从而求解出最佳的北极航线。在上述研究的基础上，可对船舶的航速做进一步分析。A.AFONIN等[5]利用包含的不同船舶有关信息的地理信息系统(GIS)，并结合冰情数据，统计处理冰区航行船舶的航速以识别航速减少的趋势；FU Shanshan等[6]建立概率模型以预测船舶在北极水域的困阻概率，并使用贝叶斯信念网络(bayesian belief networks)模型预测船舶的航速；李振福等[7]基于冰区气象的条件，分析海况对船舶的干扰力和冰阻力等因素，建立以不同冰情航速优化模型。

基于上述研究，笔者以北极东北航线为基础，建立通航期冰情条件下的混合整数双目标船舶航速优化模型。使用线性加权和离散化的方法对模型进行处理，选择MATLAB软件对模型进行求解，以期得出不同船舶的航速优化方案。

1 航线通航期冰情分析

北极东北航线的可通航时间主要集中于7月到10月[8]，将上述4个月作为通航期，并以通航期的冰情数据为基础对船舶航速进行优化分析。航线的冰情包括海冰厚度、海冰密集度等数据，目前可使用的数据库有：美国国家冰雪数据中心(National Snow & Ice Data Center)数据库、德国不来梅大学(The University of Bremen)的海冰数据库等。

选择德国不来梅大学海冰数据库中2020年7月至10月数据，对航线经过海域的海冰密集度和海冰厚度数据进行分析。

1.1 通航期海冰密集度数据分析

不来梅大学海冰数据库所提供的海冰密集度数据以HDF、netCDF等数据格式进行存储[9]，可使用相应软件进行读取。

在航线的涉及海域中，渤海在冬季部分海域开始结冰，到次年的3月海冰完全消失[10]。巴伦支海西南部存在常年无冰区，且在夏季期间出现无冰情况[11]。挪威海和北海在夏季可通航，亦不做冰情数据分析。在现有海冰密集度数据中，白令海7至10月海冰密集度均值在1%以下，其海冰密集度仅作为计算参数进行使用。因此设定楚科奇海、东西伯利亚海、拉普捷夫海以及喀拉海作为冰区海域进行分析，其通航期月均海冰密集度数据如图1。

从图1中海域的海冰密集度数据可以看出，楚科奇海在2020年的4个月的月均冰密集度呈现出较高态势，最高冰密集度接近60%。拉普捷夫海和喀拉海的月均冰密集度较低，均在10%以下。

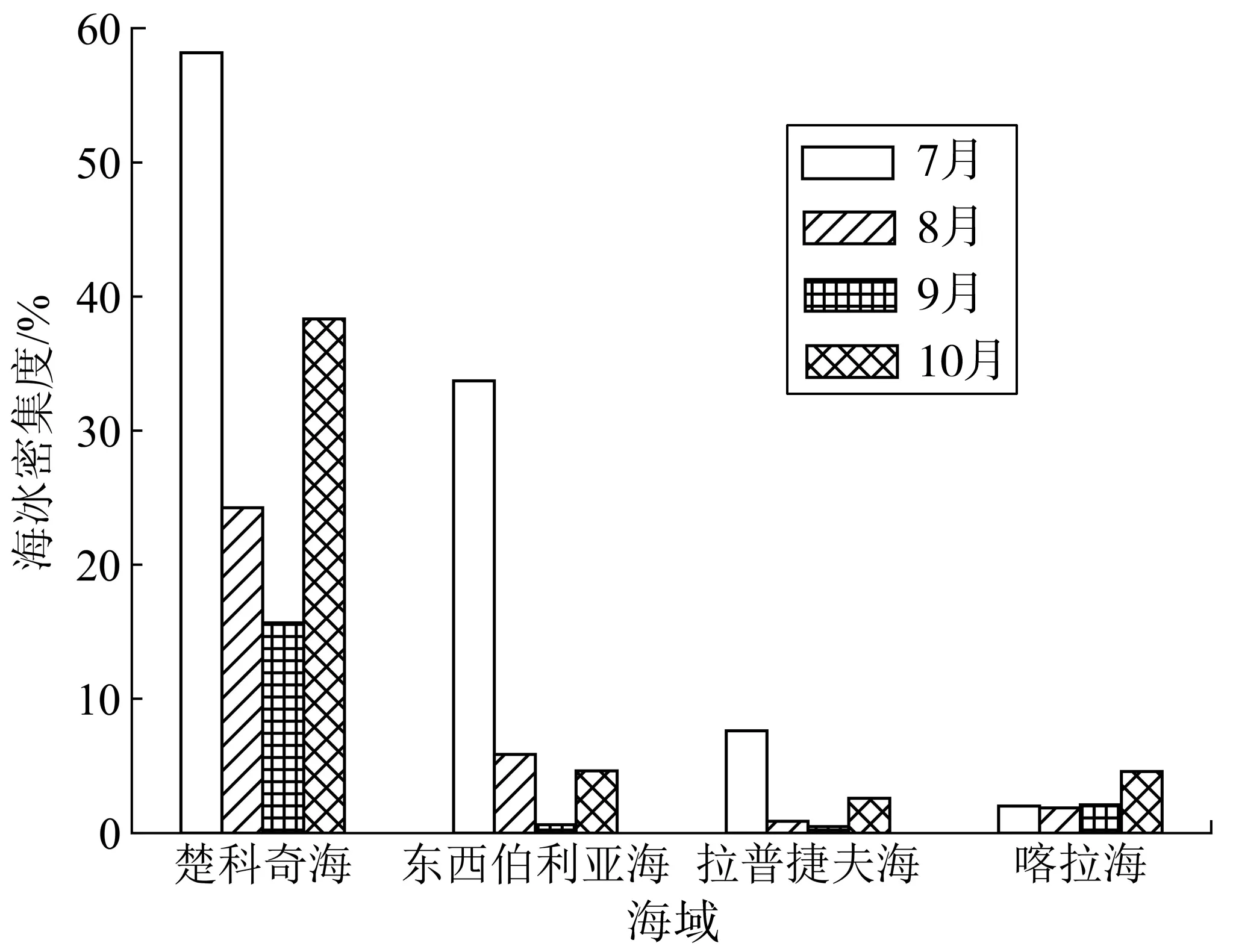
图1 冰区海域的海冰密集度

从总体来看，上述海域的冰密集度数据在8月或9月较低，但在7月或10月的波动较为剧烈。除喀拉海以外，其他3个海域在通航期4个月的变化趋势基本一致。

1.2 通航期冰厚度数据分析

使用不来梅大学海冰数据库的薄海冰厚度(the thickness of thin sea ice, SIT)库所记录的北极海冰数据[12]，其中部分数据存储于内部资料库。

选择2020年7至10月的北极海冰月均厚度数据作为后期模型求解的参考数据，不再做具体海域的数值分析，其数值如表1。

表1 海冰的月均厚度

2 船舶阻力模型构建

在冰区航行的船舶不仅要考虑水的作用效应，还要考虑海冰对船舶的影响。因此，分别对船舶的静水阻力和冰阻力进行模型构建。对阻力模型进行以下设定：①对静水阻力和冰阻力区分分析；②不考虑船舶附属体带来的附体阻力。

2.1 静水阻力模型

当船舶在无冰的静水中航行时，其所受的阻力(即裸船体阻力)f0的计算如式(1)[13]：

(1)

式中：C0为裸船体阻力的阻力系数；ρ为海水密度；v为船舶的航行速度；S为船舶的湿表面积。

船舶的湿表面积计算如式(2)[14]:

(2)

式中：Lw为船舶的水线长度；d为船舶的吃水；B为船舶的型宽；Cb为方形系数。

依据文献[13]，船舶在无冰的静水中航行所受到的阻力f0可分为摩擦阻力f1、粘压阻力f2以及兴波阻力f3：

f0=f1+f2+f3

(3)

考虑到船体表面的粗糙度，计算船舶摩擦阻力时需额外加入粗糙度补贴系数CΔ[13]。

CΔ可由船长L进行选取，其具体值如表2[7]，设定表中船长不计边界值。

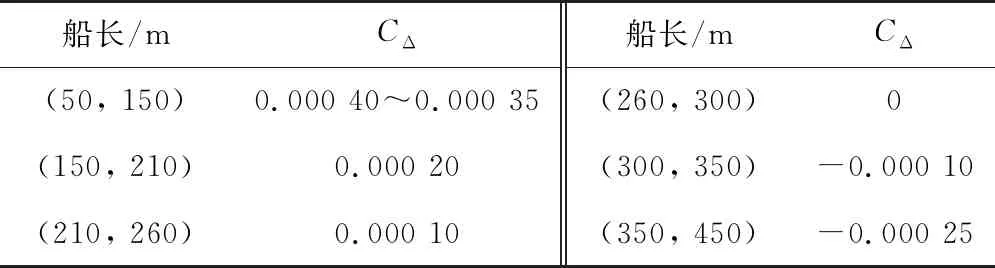
表2 粗糙度补贴系数选取

2.1.1 摩擦阻力

摩擦阻力计算如式(4)：

(4)

依据文献[13]，船舶的摩擦阻力系数可以使用1957年国际船模实验池会议所提出的计算公式：

(5)

式中：Re为雷诺数；γ为海水的运动粘性系数。

(6)

2.1.2 粘压阻力

依据文献[13]，粘压阻力系数可使用巴甫米尔提出的近似公式进行计算。粘压阻力f2和粘压阻力系数C2的计算如式(7)、式(8)：

(7)

(8)

式中：Am为船舶中横剖面的水线下面积，后简称为中横剖面积。Am可通过式(9)进行计算，Cm为中横剖面系数。

Am=CmBd

(9)

Lr为船舶的去流段长度，为了避免严重的船舶的航行漩涡效应，选取去流段长度为[15]：

(10)

2.1.3 兴波阻力

通过对Michell积分进行简化，可对兴波阻力进行计算[16]。具体公式如式(11)：

(11)

式中：λ=secθ，θ为凯尔文波系(Kelvin wave system)相对于x轴的角；ω1与ω2与船舶表面函数的纵向梯度有关。

简化后的兴波阻力公式也难以直接计算出船舶受到的兴波阻力。而文献[17]提供的测试程序可进行简化测算，该程序通过计算Michell积分来估计Wigley船型的波阻力，且提供的阻力数据可作为计算兴波阻力的基础。

首先，在上述测试程序中输入相应的船舶参数，运行程序得到多航速对应的阻力数据。其次，对结果数据进行MATLAB的傅里叶级数拟合，得到多参数的兴波阻力和船舶航速的拟合函数，其拟合函数如式(12)：

(12)

式中：a0、aj、bj以及z为对应的拟合参数。

2.2 冰阻力模型

设定船舶在通航期航行所受到冰阻力为浮冰(pack ice)阻力fe，可由式(13)进行计算[18]。

fe=CeρegBhv2Wn

(13)

式中：ρe为海冰密度；h为海冰厚度；W为海冰密集度；Ce浮冰阻力系数；n为海冰密集度的幂次数；g为重力加速度。依据文献[18]，使用n=2对于计算具有极小的误差。

依据文献[18]，加拿大海洋技术研究所经过多年试验得出lnCe和lnFr呈线性关系，Ce和Fr的关系如式(14)。

Ce=4.4Fr-0.8267

(14)

式中：Fr为浮冰的弗劳德数，计算如式(15)：

(15)

3 航速优化模型构建

3.1 问题概述

在传统航线的运营中，船舶通常有固定的挂靠港口[19]，且在港口间的货运量相对确定。船公司可以根据自身的经营状况，对航线上运营的多种船舶进行合理调配，以期得到最大的经济效益。

在北极航线中，船舶一般只在通航期进行航行，难以在航线内进行多航段和多船组合的调配。因此，在现有船舶条件下，建立北极航线单船单航次的双目标航速优化模型，在船舶的港口使费、固定成本及燃油成本在内的运营成本最低，以及船舶的航行时间和停泊时间在内的运营时间达到最低的条件下，并求解船舶的最佳航速。依据第2节中的船舶阻力公式，可对船舶克服阻力进行航行的做功进行转化求出船舶的燃油成本，进而确定船舶运营成本。同时对航线进行航段划分，使不同船舶的航速在不同航段达到最优。对船舶的航行过程做出3点假设：①航线上仅配置单个船舶，且船舶在航线的每个航段匀速航行；②不考虑航线极端气象状况，选取理想航行状态。③不使用额外破冰船进行辅助航行。

3.2 规划模型

第1个目标函数如式(16)，表示船舶完成航线航行的运营成本最小化。式(16)由船舶的港口使费、船舶航行的固定成本、船舶的燃油成本3个部分构成。

(16)

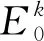
第2个目标函数如式(17)，表示船舶完成航线航行的运营时间最小化。式(17)由船舶航行时间、船舶停泊时间两部分组成。

(17)

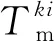
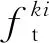
(18)

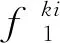
使用燃油的燃烧热值对船舶做功进行燃油量的换算，从而求出燃油成本。船舶的燃机和传动机构复杂，难以计算其实际效率，因此不计船舶的能量损耗。

(19)

式中：DL为轻质燃油单位价格；DH为重质燃油单位价格；ε1为轻质燃油的燃烧热值；ε2为重质燃油的燃烧热值；vki为船舶k在i航段的航速。

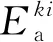
(20)

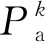
船舶于不同航段的航行时间如式(21)，分为3项：第1项为冰区航段的船舶航行时间；第2项为ECA航段的船舶航行时间；第3项为普通航段的船舶航行时间。

(21)

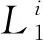
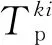
(22)

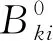
航段的航速限制范围如式(23)：

(23)

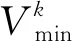
式(24)表示航线只能使用单个船舶k。

(24)

4 算例的求解与分析

4.1 算法设计

建立的航速优化模型为双目标模型，两个目标函数均为线性函数，且存在离散化的参数条件。求解上述模型可使用线性加权法或启发式算法。启发式算法的求解速度较快，但求解结果通常为近似最优解。因此，针对双目标航速优化模型，使用线性加权法进行离散化求解。求解软件为MATLAB，求解步骤为：

1)使用线性加权法进行重要度赋权，将多目标问题转化为单目标混合整数规划问题。设置相应权值∂1和∂2，构造新目标函数Y3：

minY3=∂1Y1+∂2Y2

(25)

2)根据多船舶和多航段条件进行目标问题拆分，使决策变量xk失效，目标问题从而离散化为若干个一般的线性规划子问题。

3)使用MATLAB求解上述若干子问题，得出对应的最优解。

4.2 船舶信息

选择4艘冰级运输船作为算例，船舶具体类型分别为：杂货运输船、集装箱运输船、原油运输船、液化天然气运输船。上述船舶基于俄罗斯船级社标准的冰级分别为：Arc 4、Arc 4、Arc 7、Arc 7。船舶具体数据如表3。

表3 船舶数据

基于现有海冰密集度和海冰厚度数据，设定中度冰情(冰密集度在30%～60%和冰厚度在30 cm内)时船舶应按照预定航速的80%进行航行[4]。有冰情数据但低于上述值时，设为轻度冰情。船舶航速的80%为冰区航段中度冰情时的安全航速范围。

4.3 航线的航段划分

算例航线选择天津港为起始挂靠港，鹿特丹港为终止挂靠港。并以符拉迪沃斯托克、彼得罗巴甫洛夫斯克、普罗维杰尼亚、佩韦克、季克西、迪克森以及摩尔曼斯克的港口为基准港进行航线长度的测算。设定船舶物资储备充足，可满足船舶完成航行的需求，船舶不挂靠基准港。设定船舶在起始港装载货物，在终止港卸载货物。整条航线按照航行海域可划分11个航段，航线内有1个起始港、1个终止港、7个途经港。

对航线的航段划分做出以下设定：①对部分基准港区间内的非冰区海域进行整体航段划分;②可收集到冰情数据(海冰密集度、海冰厚度)的海域跨越多基准港区间时：基于离散化的方法，对上述涉及海域的航段进行分属基准港区间的子航段划分。同属一个海域的子航段的冰情参数和海水参数取值一致。为避免基准港区间的干扰，选取同海域的第一个子航段的航速作为航速分析的基础。航线的总体航段划分如表4。

表4 航线的总体航段划分

4.4 优化结果分析

针对船舶的燃油成本，重质燃油的参考价格为430美元/t，轻质燃油的参考价格为530美元/t。在起始港，选取包括船舶停泊和引航(移泊)费用、货物的港务费在内的港口使费，终止港视具体规定进行选取。依据既定条件对模型进行求解，可得出算例船舶在多航段中的不同月的最优航速，航速单位为kn。

表5为4艘船舶航速的优化结果。从表5可以看出，在非冰区航段，4艘船舶的航速波动较小，其航速均值分别为14.88、14.46、13.39、16.12 kn。而在冰区航段，相较于非冰区航段其航速有所下降，船舶在中度冰情航段航速均值分别为：12.72、12.42、11.86、13.91 kn。

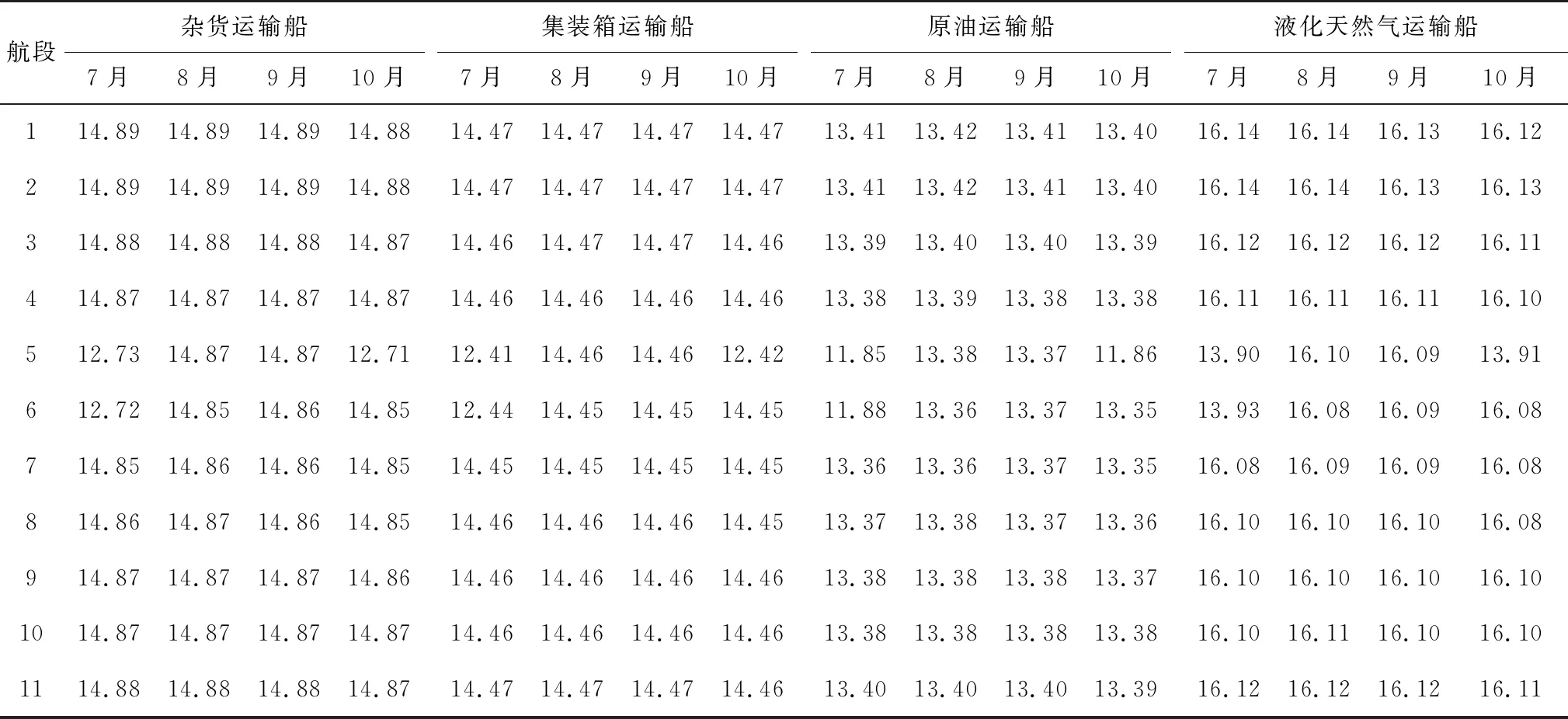
表5 船舶的最优航速

图2为4艘船舶在非冰区航段和冰区航段通航期不同月份的航速对比，冰区航段出现中度冰情显示有降幅航速的均值。图3为航速优化后的单航次船舶运营成本和运营时间。

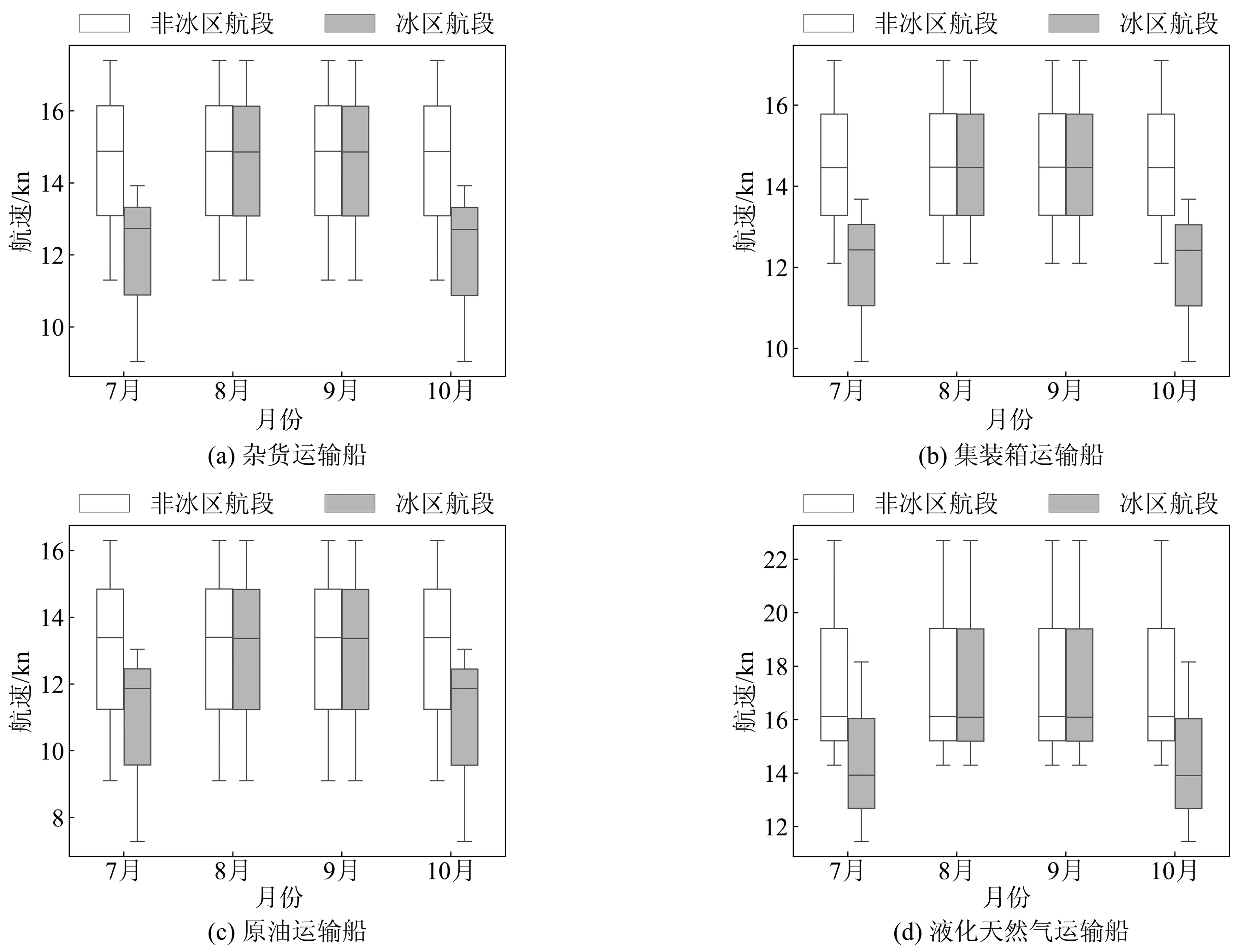
图2 船舶航速对比

由图2可知：在非冰区航段，船舶的航速无明显变化。而在冰区的中度冰情航段，船舶的航速有一定的降幅。依据表5的数据，在中度冰情航段，4艘船舶的航速均值相较非冰区航段的降幅最大达到14.53%、14.12%、11.41%、13.67%。由图3可知，通航期冰情变化对船舶的运营成本以及运营时间的影响较小。因此，笔者所构建的模型能够较好的反映船舶在北极航线通航期的实际航行状态。

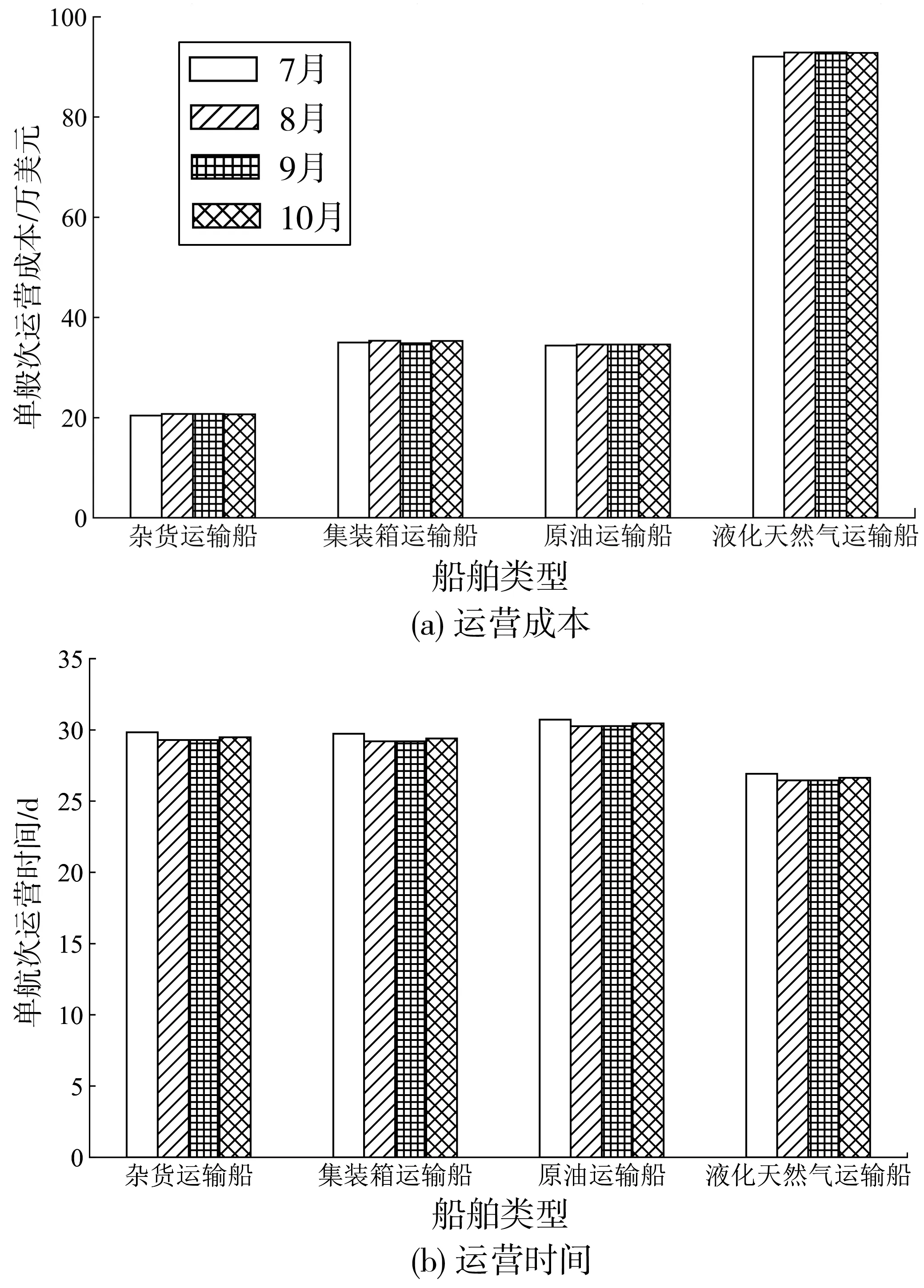
图3 单航次运营成本和运营时间

5 结 论

笔者对北极东北航线的通航期冰情数据进行分析，考虑船舶的阻力因素，建立以船舶单航次的运营成本和运营时间最低为目标的航速优化模型。其次，使用线性加权和离散化的方法处理所建立的模型。最后，使用MATLAB软件对模型进行求解，得出多种船舶不同航段的最优航速。从航速结果可以看出，在非冰区航段的船舶航速变化较小，而在中度冰情的条件下船舶航速有一定的降幅。相较非冰区航段，4艘算例船舶在中度冰情航段的航速均值最大降幅达到14.53%、14.12%、11.41%、13.67%。