Quick identification of guidance law for an incoming missile using multiple-model mechanism

Yinhn WANG， Shipeng FAN，*， Jing WANG， Gung WU

a School of Aerospace Engineers， Beijing Institute of Technology， Beijing 100081， China

b Beijing Aerospace Automatic Institute， Beijing 100854， China

KEYWORDS Gated recurrent unit;Multiple-model mechanism;Neural networks;Parameter identification;Regression models

Abstract A guidance law parameter identification model based on Gated Recurrent Unit (GRU)neural network is established.The scenario of the model is that an incoming missile(called missile)attacks a target aircraft (called aircraft) using Proportional Navigation (PN) guidance law. The parameter identification is viewed as a regression problem in this paper rather than a classification problem，which means the assumption that the parameter is in a finite set of possible results is discarded.To increase the training speed of the neural network and obtain the nonlinear mapping relationship between kinematic information and the guidance law parameter of the incoming missile，an output processing method called Multiple-Model Mechanism(MMM)is proposed.Compared with a conventional GRU neural network，the model established in this paper can deal with data of any length through an encoding layer in front of the input layer. The effectiveness of the proposed Multiple-Model Mechanism and the performance of the guidance law parameter identification model are demonstrated using numerical simulation.

1. Introduction

With the development of guidance law，the survival pressure of aircraft is increasing.To counter the advancement and improve the survivability of aircraft， a significant number of approaches have been proposed.These approaches can be generally divided into two categories:differential gameor random maneuver. No matter which method is adopted，knowledge of the missile’s guidance law parameter will offer the aircraft a priority.

There are few literatures on missile guidance law parameter identification. In Ref. 13， an algorithm based on Multiple-Model Adaptive Estimator (MMAE) is presented. The main idea is to set a bank of Kalman filters， with each filter representing a possible guidance law. The guidance law is obtained by comparing measurement data with the output data of each filter. In Ref.， a modified interactive multiple-model filter is proposed to solve the problem. The method minimizes the degradation of estimation performance by systematic approach for the different state vectors.In the pioneering work 15， a nonlinear MMAE method based on unscented Kalman filter is proposed to identify the guidance law in three dimensional coordinates. In most previous studies， the identification model is established based on Kalman filter，which has the following significant drawbacks:

(1) The transient process of the model is generally more than one second，which means there is a relatively harsh continuous acquisition requirement on missile’s information. The stolidity might limit the maneuverability of aircraft and thus threat the safety of it.

(2) The guidance law parameter identification is generally solved as a classification problem under the assumption that the system is in a finite set of possible results known by the aircraft in advance because the update of the Kalman filter stems from the difference between measurement data and the output of the Kalman filter. In the case that the assumption doesn’t hold， the performance of the model might decrease.

With the development of computing and storage capacity，Artificial Neural Network (ANN)， which can analyze and extract features from a large number of prior data， has been widely used.Among all kinds of ANN， Long Short-Term Memory(LSTM) is outstanding in dealing with timerelated problems.Gated recurrent unitis a simplicity of LSTM with faster training speed. In Ref. 30， a parameter law parameter identification model based on GRU neural network is established， and the required identification time is shortened to less than 0.5 s.However，the problem is still solved as a classification problem in Ref. 30. This paper is based on and is an improvement to Ref.30.A regression parameter identification model is established in this paper. The input of the model is the kinematics information between the missile and the aircraft， while the output is the guidance law parameter.To increase the training speed and the accuracy of the neural network model， an output processing method known as MMM is proposed in this paper.In most previous GRU neural network studies，only the output at the last moment is investigated.This paper does further research，extracting and analyzing the transient process of the inner state at different times by adding an encoding layer in front of the input layer.

The PN guidance law is a popular navigation law widely employed in missile-target evasion because of its simplicity，robustness， and ease of implementation.In many scenarios，it is practical to make the assumption that the guidance law of the missile is PN guidance law，and the guidance law parameter is set to a constant.Therefore， in this paper， we only focus on the PN guidance law.

The rest of this paper is organized as follows.The next section presents the mathematical model of missile-target engagement， as well as an analysis for the characteristics of the guidance law parameter identification problem. The concept of MMM and the structure of the identification model are presented in Section 3， followed by the derivation of the training process of GRU neural network with MMM in Section 4.The numerical simulation results are presented and analyzed in Section 5. Finally， concluding remarks are given in Section 6.

2. Problem formulation

This section presents the nonlinear dynamics model of the missile-target engagement， followed by an analysis for the characteristics of the guidance law parameter identification problem.

2.1. Nonlinear dynamic model

The engagement for an incoming missile attacking a target aircraft is described in a Cartesian inertial coordinate system， as shown in Fig.1.The missile is launched at the origin.The variables associated with the missile and aircraft are denoted by the subscripts M and A， respectively. The velocity， acceleration， elevation angle， and azimuth angle are denoted by v， a，θ， and ψ， respectively. The Line-Of-Sight (LOS) angle in the vertical and horizontal plane are denoted by qand q，respectively.

Assuming that both the missile and the aircraft are skid-toturn roll-stabilized， the engagement kinematics can be expressed as

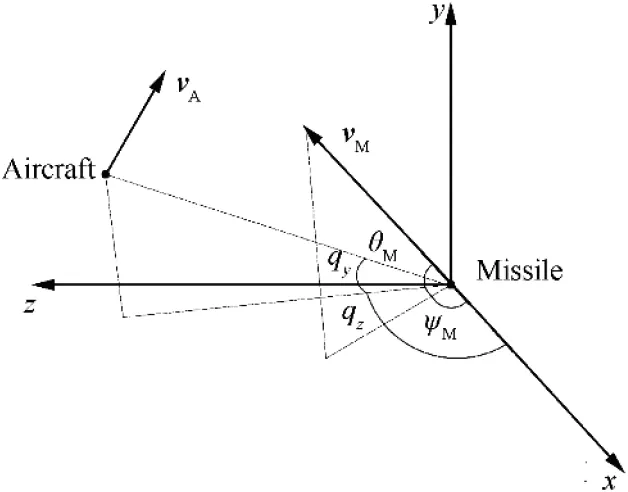
Fig. 1 Inertial coordinate system.

where R is the relative distance between missile and aircraft;x，y， and zare relative distance in x， y， and z axis， respectively.

2.2. Characteristics of guidance law parameter identification

The missile implementing different guidance law parameter attacks the aircraft along trajectories with different curvature，as shown in Fig. 2. There is a nonlinear complex mapping relationship between relative kinematic information and the guidance law parameter.The input of the problem is an episode of the kinematic information， while the output is the guidance law parameter. The key point to solve the problem is to find the nonlinear mapping relationship between the input and the output.

3. Parameter identification model

Remark 1. The identification of guidance law parameter is solved as a regression problem related to time in this paper.And GRU neural network has a good performance in dealing with such problems.

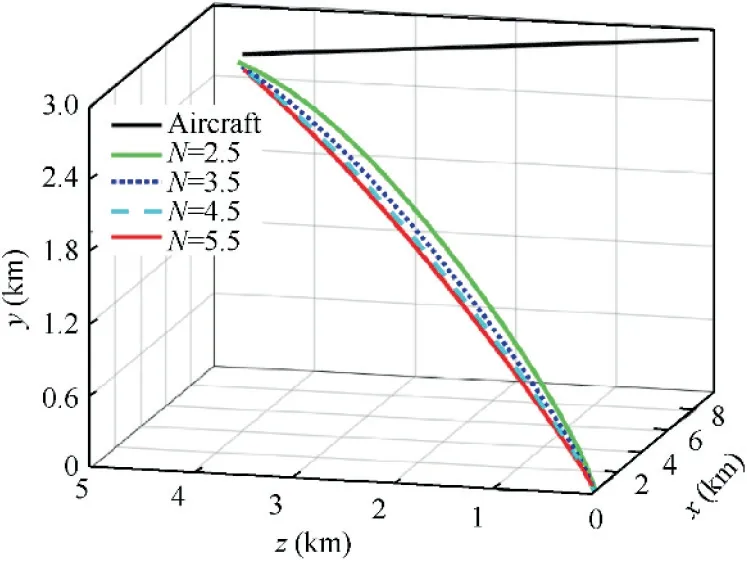
Fig. 2 Different parameters correspond to different trajectories.

In this section， we firstly present the defects of the conventional neural network in the regression problem. To improve the defects， the MMM is proposed in this paper. The concept of the GRU neural network and the structure of the identification model based on the GRU neural network with MMM are presented at the end of the section.

Notations. For simplicity， in the following of this paper，sigmoid，tanh and softmax denote different activation function as follows:

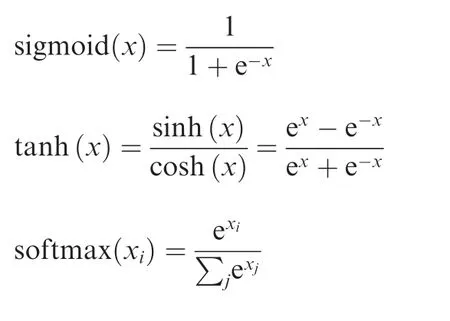
3.1. Multiple-model mechanism

The structure of a conventional neural network in the regression problem is shown in Fig. 3， where x is the input data to the neural network; N is the regression result.

There are three different types of layers in the conventional neural network. The input layer is used for processing input data.The hidden layer is the main part of the neural network，consisting of hidden neurons to extract information from the input data. The output layer is a fully-connected layer， and the regression result is the sum of the output of the last hidden layer. The initial output range of the neural network is influenced by the number of neurons， depth of the neural network， initialization method， et al. So， the first stage of the training process is to compress or extend the output of the neural network (e.g.， ［0，b］，［a，b］，［a，b］) equal to the required range (［a，b］)， as shown in Fig. 4.

However， the required range is reflected in the dataset and could be obtained before training. To this end， ideas of multiple-model adaptive estimator and Kalman filter are introduced to the neural network，and an output processing method using Multiple-Model Mechanism is proposed in this paper.Add a multiple-model layer behind the conventional neural network， in which regimes， similar to Kalman filters in MMAE， are constructedas the structure of a neural network using MMM is shown in Fig. 5， where Ris the value of j th regime and Gis the weight of j th regime. The number of the model is set before training. Each regime represents a different quantity.The output of the neural network is weights of different regimes，and the regression result is a weighted sum of each quantity.

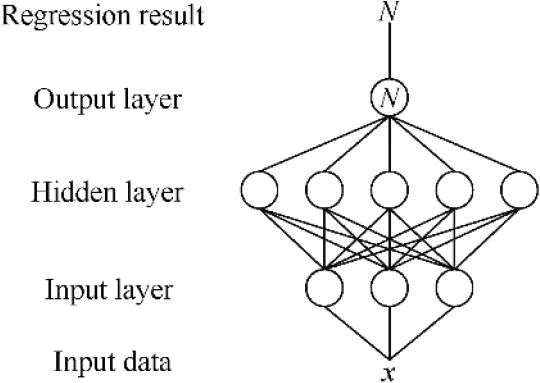
Fig. 3 Structure of a conventional neural network in the regression problem.

Weights of different regimes are obtained through the output layer. The activation function of the output layer is softmax， which makes the sum of weights of regimes equal to one:

Let the maximum value of regimes a little larger than the maximum label of the training dataset， while the minimum value a little smaller than the minimum label of the training dataset.Therefore， according to Eqs.(11) and(12)， the identification result of the neural network is limited to the required range before training.

Remark 2. The MMAE is a static multiple-model estimator，addressing a scenario in which the solution of the problem is within a known finite set of possible results. The correct probabilities of different regimes are represented by the weights.In MMM， the concept of regimes is adopted to limit the regression result of the neural network to the required range，and the weights represent the proportion of different regimes.

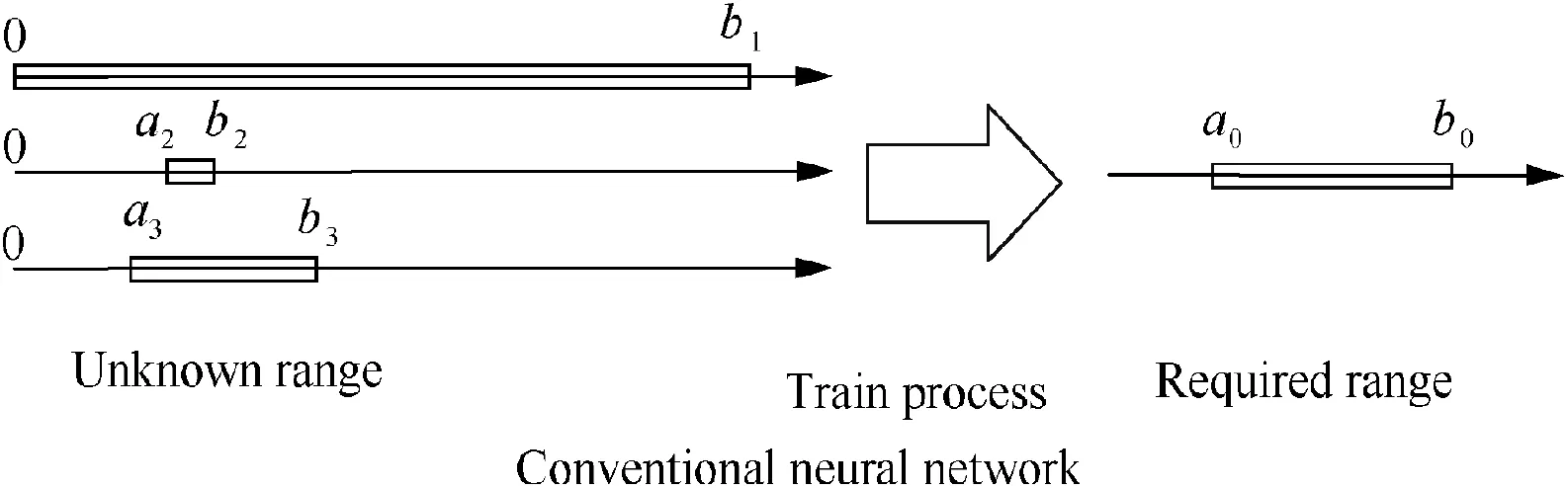
Fig. 4 First stage of the training process of conventional neural network.

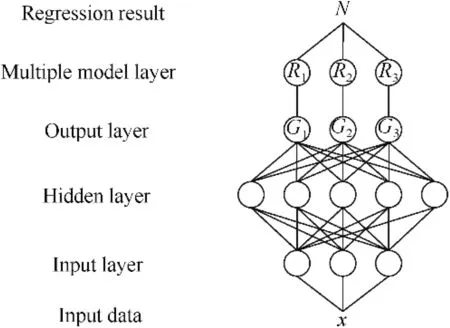
Fig. 5 Structure of the neural network with MMM.

Different from the conventional neural network shown in Fig. 4， the weights of different regimes instead of the absolute output result are emphasized in MMM， as shown in Fig. 6.

3.2. Structure of parameter identification model

where σ is the sigmoid function;w is the weight matrix;b is the bias vector; · is the matrix multiply; and × is multiply by element.

The identification models based on GRU neural network with and without MMM are shown in Fig. 8， where Mis the measurement data; xis the input data to neural network;GRU（i，n）is i th hidden layer，whose neuron number is n;wis the weight of j th regime; Nis the identification result; m is the period of the measurement data; l is the input step of the model.

The preset input step of the model is denoted as K. In the encoding layer，if the period of the measurement data m is less than K， then the input step of the model l is set as m. Otherwise，the input data of the model is set by sliding windows with time overlap，i.e.，

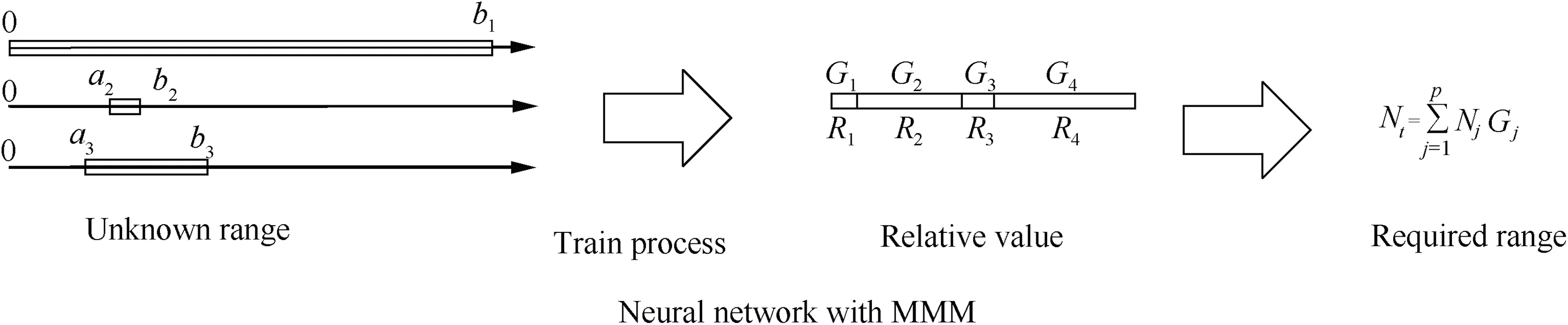
Fig. 6 Difference between conventional neural network and neural network with MMM.

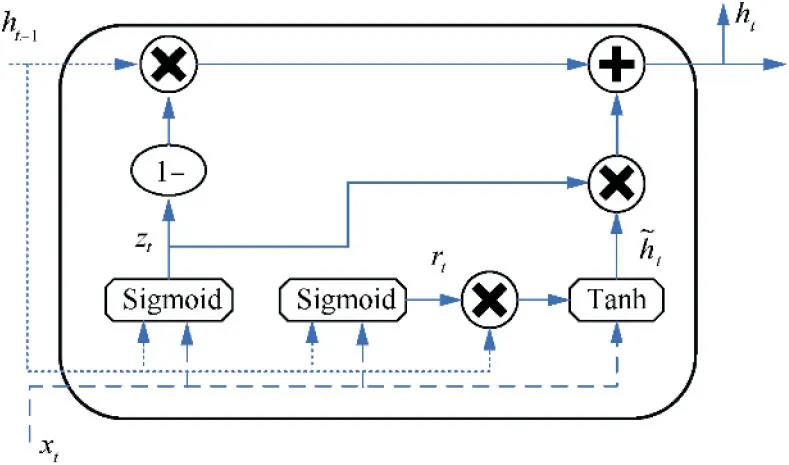
Fig. 7 Structure of basic GRU neuron.

4. Training method

This section presents the dataset establishing method，followed by the derivation of the training process of GRU neural network with MMM.

4.1. Dataset establishment

Sliding window is adopted to extract information from the nonlinear dynamic model in Section 2 and to form the samples，as shown in Fig. 9.

Remark 3. We assume the missile is guided towards the aircraft using PN guidance law. If the assumption does not hold， similar identification models to identify guidance law and to obtain parameters of different guidance law (e.g.， N of augmented proportional navigation law and α of optimal guidance law) can be established and trained using the method proposed in this paper.

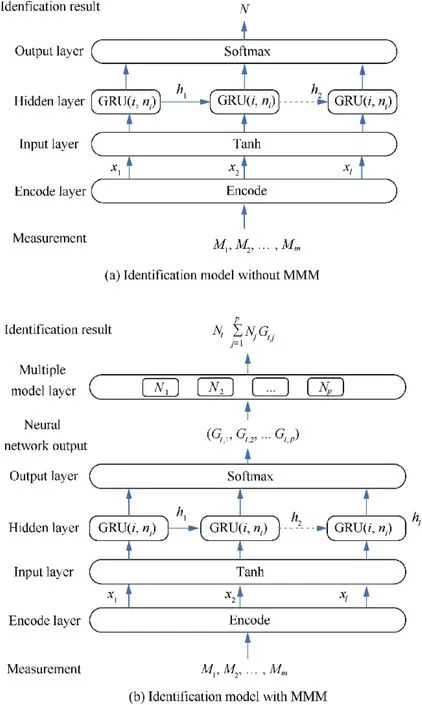
Fig. 8 Identification model based on GRU.

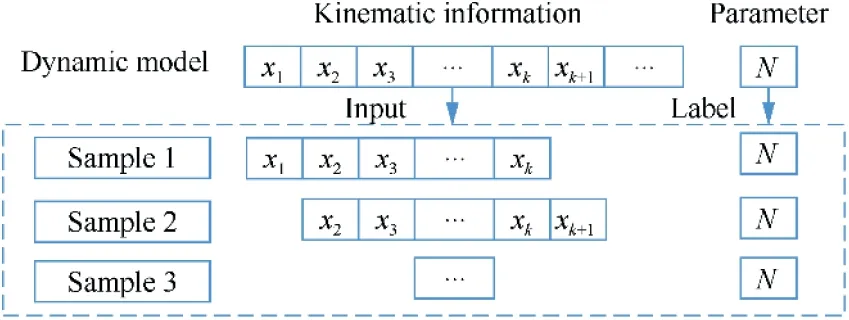
Fig. 9 Demonstration of sliding windows.

The label of the sample is a different guidance law parameter. To increase the training speed of the model， besides the measurement information in Eq. (9)， the differential of measurement is also defined as input data， i.e.，

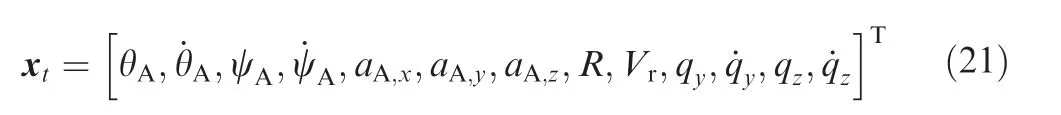
where Lis the label of a sample; Nand Nare preset experimentally instead of the maximum or minimum value of guidance law parameter in the dataset.

4.2. Training process

Remark 4. The loss function of the identification model established in this paper is the Mean Square Error (MSE) instead of the cross-entropy， which is widely used to solve classification problem. Therefore， although softmax is adopted as the activation function of the last layer， the training formula is different from the conventional classification neural network.

The training of a neural network is to adjust the parameters to reduce the value of the loss function. The trainable parameters include weight matrixes and the bias of the input layer，hidden layers， and output layer. Define the error gradient of the parameters along the parameter c as follows:

5. Numerical simulation

The performance of the proposed network with MMM and the established identification model are evaluated in this section via numerical simulation.Firstly，the performance comparison between the identification model based on the conventional GRU neural network and GRU neural network with proposed method is carried out. Then， the impact of the input step and noise is presented.The transient process of the identification is presented at the end of this section.

5.1. Engagement scenario and parameters

where Ais the available amplitude; f is the frequency. The parameters are set as A＝30， f ＝0.2， ψ（0 ）＝－45.tial learning rate is 0.00025，and the learning rate decaying rate is 0.95/100 iterations.To prevent over-fitting of the neural network，dropout regularization is adopted in this paper，with the dropout rate set to 5%. The Adam algorithm parameters are set to ∈＝10， η＝0.9， η＝0.999.

5.2. Performance of proposed method

The identification models based on GRU neural network with and without MMM are established in Section 3 respectively.The number of the hidden layer is 3， and each layer contains 80 basic GRU neurons. The preset input step is K ＝25. The loss function of both neural networks is MSE. The training process is depicted in Fig. 10. It can be found that compared with the conventional model，the initial MSE of the model with MMM reduces from 0.2957 to 0.0477， validating the theoretical analysis in Section 3. And it can also be observed that the MSE after the training of the model with MMM is less than that of conventional model， which means the former has higher identification accuracy.

The measurements of the aircraft are contaminated by a zero-mean white Gaussian noise，as expressed in Eqs. (9)and (10). The noise is defined in

The performance of the identification model under different noise is presented in Fig. 11. It can be observed that with the increase in noise level，the accuracy of the identification model gets lower. The effect of the input step on the performance of the model with the proposed method is depicted in Fig. 12.It can be found that when the input step is less than 25， i.e.，the identification time is less than 0.5 s，it would lead to degradation of the identification performance.

5.3. Transient process

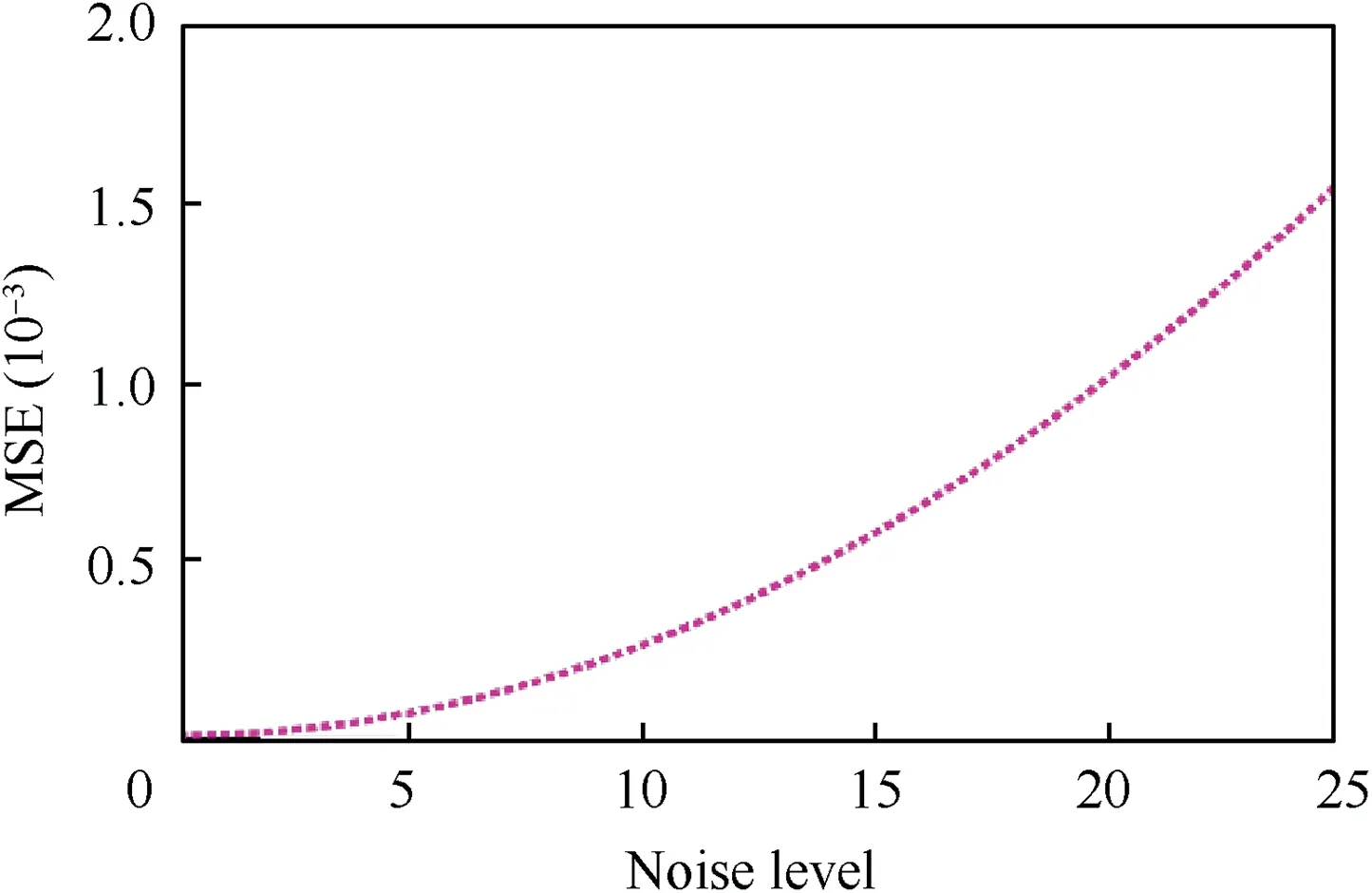
Fig. 11 Performance with regard to noise.

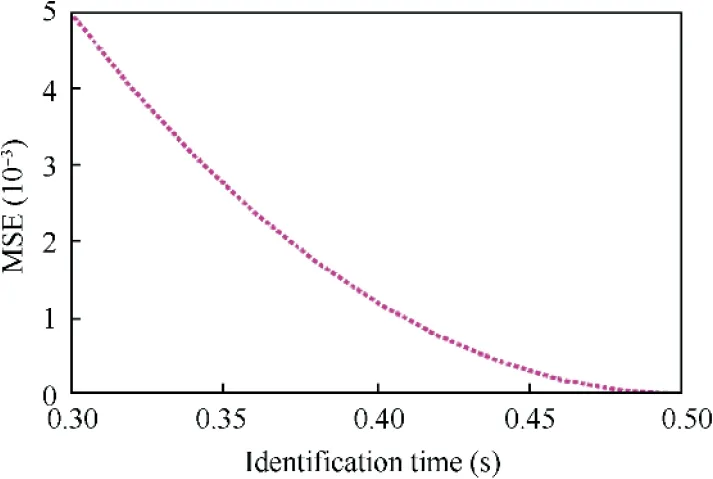
Fig. 12 Performance with regard to identification time.

Fig.13 presents the transient process of weights of each regime and identification results in three cases: N ＝2.5，4.0，5.5. The weights of each regime are equal in theory at t ＝0， so identification result at t ＝0 is 4.0. In all cases， the identification result of the model converges to the real value in 0.5 s without fierce fluctuations， which verify the rapidness and stability of the model. Under the computer environment of this paper，the calculation time of the identification model is 0.1936 ms，which could be ignored compared with transient process time 0.5 s.

The missile may not be detected by aircraft at the moment of launch. Assume that the missile is captured by the radar of aircraft in tseconds after the missile is launched. Fig. 14 presents transient process of different t. It can be found that the model performs a more stable convergence process with the closer distance to the missile.The reason for this phenomenon is that the observability of the measurements is closely related to the range between the missile and the aircraft， more precisely， the maneuver of the missile lured by the aircraft is generally more intense with a smaller range.

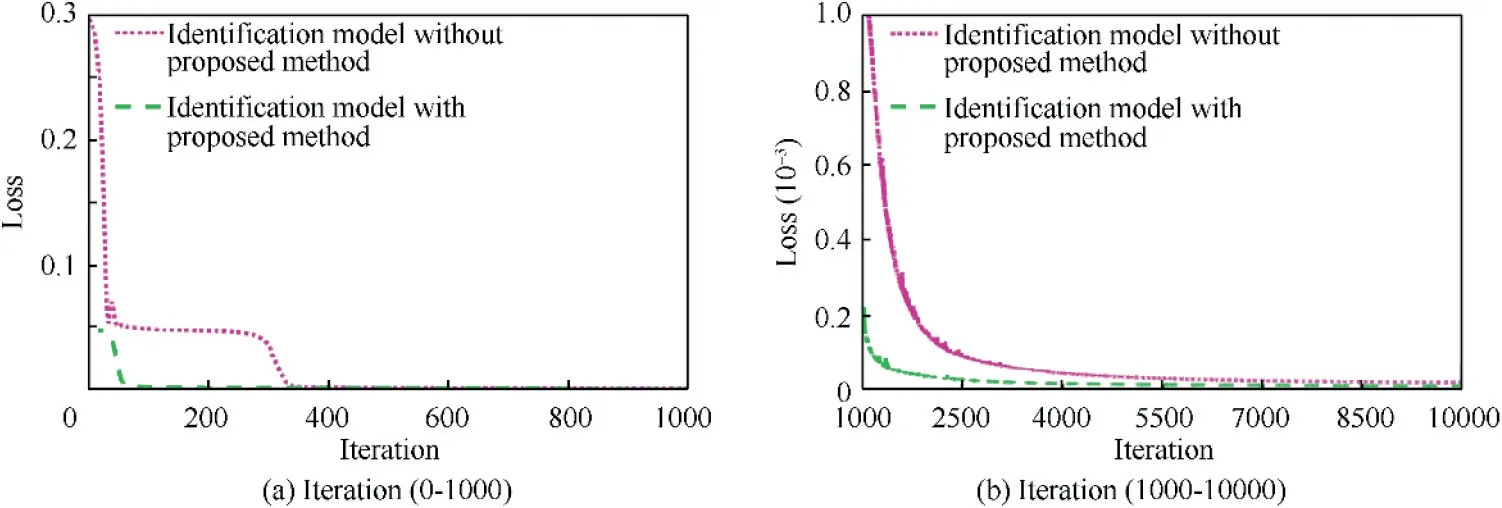
Fig. 10 MSE of two neural networks.

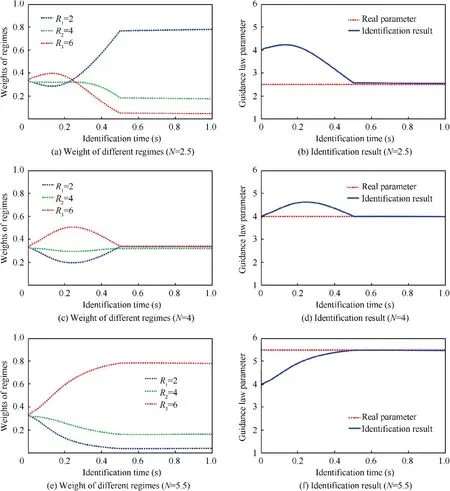
Fig. 13 Transient process of different N.

The required identification time (the minimal length of input data to make the model achieve the reliability) and the average computation time of different methods is presented in Table 1， in which the reliability means the probability of the true regime for Kalman filter， accuracy for classification GRU neural network， and MSE for regression GRU neural network. It can be found that the required identification time of the identification model based on GRU neural network is generally within 0.5 s and has a notable reduction compared with the Kalman filter.The reason for the phenomenon is that the identification model based on the Kalman filter has a relatively long transient process，while the identification process is shortened in the model based on GRU neural network by training with a large number of prior data， i.e.， training samples.

In Ref.30 the guidance law parameter identification is generally regarded as a classification problem under the assumption that the system is in a finite set of possible results known by the aircraft in advance. The simplicity assumption is discarded in the regression model established in this paper.Therefore， the required identification time of the regression model based on GRU neural network with the proposed method is longer than that of the classification model based on GRU neural network， as shown in Table 1. Besides， it can also be found from the last column of the table that the average computation time of all the different methods is less than 0.2 ms， which means it could be ignored compared with the required identification time.

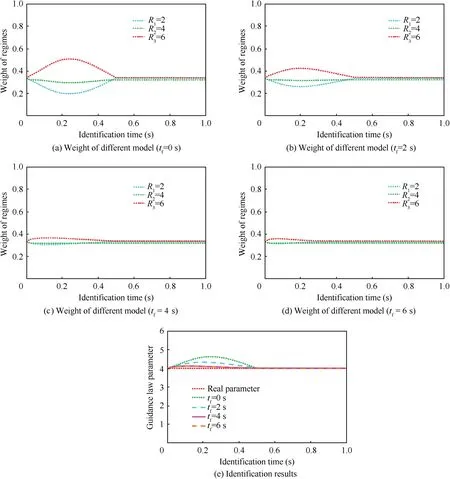
Fig. 14 Transient process at different find time.

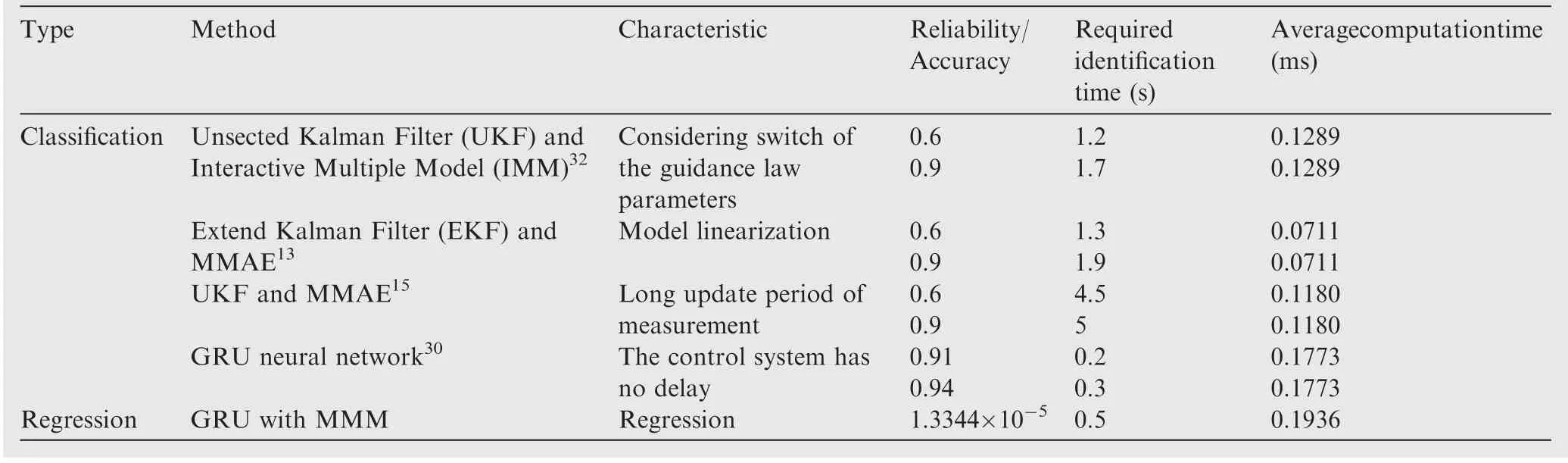
Table 1 CPU time ratio of each term.

6. Concluding remarks

Considering a scenario in which an incoming missile attacks a target aircraft using proportional navigation guidance law， a guidance law parameter identification model based on GRU neural network is established. The input of the network is the kinematic information of the missile and the aircraft， and the output is the guidance law parameter. The performance of the model is verified by numerical simulations. Compared with Kalman filter，the proposed method is faster，as the transient process of the neural network is shortened to less than 0.5 s.

To increase the training speed and accuracy of the model，an output processing network with MMM is proposed. In MMM，the concept of regime is utilized to limit the regression result of a neural network in the required range.The weights of different regimes，instead of absolute output result，are emphasized in MMM. Simulation results demonstrate that the identification model with proposed method has a better performance than the conventional model.

In addition， despite the assumption that the missile is guided towards the aircraft using PN guidance law，the models can be modified conveniently to easily extend to other various guidance laws.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgement

This study was supported by the Airforce Advance Research Project of China (No. 3030209).