Capture and detumbling control for active debris removal by a dual-arm space robot

Dong HAN， Gangqi DONG，*， Panfeng HUANG， Zhiqing MA

a National Key Laboratory of Aerospace Flight Dynamics， Northwestern Polytechnical University， Xi’an 710072， China

b Research Center for Intelligent Robotics， School of Astronautics， Northwestern Polytechnical University， Xi’an 710072， China

KEYWORDS Active debris removal;Adaptive backstepping control;Compliant clamping control;Prescribed trajectory tracking;Space robot

Abstract Active debris removal (ADR) technology is an effective approach to remediate the proliferation of space debris，which seriously threatens the operational safety of orbital spacecraft.This study aims to design a controller for a dual-arm space robot to capture tumbling debris， including capture control and detumbling control. Typical space debris is considered as a non-cooperative target， which has no specific capture points and unknown dynamic parameters. Compliant clamping control and the adaptive backstepping-based prescribed trajectory tracking control (PTTC)method are proposed in this paper. First， the differential geometry theory is utilized to establish the constraint equations， the dynamic model of the chaser-target system is obtained by applying the Hamilton variational principle， and the compliance clamping controller is further designed to capture the non-cooperative target without contact force feedback.Next，in the post-capture phase，an adaptive backstepping-based PTTC is proposed to detumble the combined spacecraft in the presence of model uncertainties. Finally， numerical simulations are carried out to validate the feasibility of the proposed capture and detumbling control method.Simulation results indicate that the target detumbling achieved by the PTTC method can reduce propellant consumption by up to 24.11%.

1. Introduction

The amount of space debris increase as human space development activities accelerate.Space debris not only poses a serious threat to spacecraft safety， but also affects the launching of new satellites.Active debris removal (ADR) has received much attention in recent years to address the space debris problem. According to NASA from the beginning of 2020，at least five large-scale debris targets (e.g.， malfunctioning satellite， rocket upper stages， remnants of explosions， etc.)need to be removed each year to maintain the orbit environment.Recently， major aerospace countries have begun research into ADR technology and actively carried out key technology testing and verification tasks， such as ETS-VII，CSO，RemoveDEBRIS，and AnDROiD.However， these projects mainly focus on cooperative targets，while orbital debris generally does not have a specific docking interface or even tumbling due to their residual angular momentum.Therefore， the capture and detumbling of such non-cooperative targets remain a major research challenge.

Flexible tools， including tether netsand tether grippers，are currently used to capture targets without a specific capture point. These methods require the consideration of target shape feature， and in practice， they are difficult to control because of their flexible nature.Low reusability is another intrinsic weakness of tether systems. In contrast，a robotic arm with a customized end-effector was developed to achieve debris capture with high reliability and reusability. Wei， et al.focused on collision impact reduction， introducing the ‘‘dynamic grasping area” concept to control the end-effector constricting speed. Simulations indicated that the grasping strategy was superior to accelerate grasping.Aghilipresented an optimal guidance scheme for smooth robotic capturing of a tumbling target， taking the zero relative velocity between the end-effector and the grapple fixture as the optimization index. Compared with the single-arm space robot， the dual-arm robot could provide better contact stability. At the same time， in the closed-chain structure composed of the space robot and the target， the dual-arm system could maintain the movement flexibility of the grasped object. Huang et al.investigated a dynamic balance control method， using a mission arm capture the target，while a balance arm was utilized to keep the base fixed in the inertial frame. A relationship between the motions of the two arms was established that could realize zero reaction to the base. Xu et al.proposed a dual-arm coordinated‘‘Area-Oriented Capture” (AOC) approach， where a plane，rather than a point， was taken as the capture interface， making target capture more tolerant and efficient. Impedance-PD control and hybrid impedance/position control were adopted to achieve target capture，and the hybrid control method significantly improved the control system robustness. Similarly， a clamping strategy based on multispace hybrid impedance control was designed to achieve a precise contact force， and a dual-arm extended Jacobian matrix was applied to stabilize the attitude of the base，which could steadily reduce the angular velocity of the tumbling target. However， all these control methods require an accurate contact force sensor and sufficient computing resources to solve the inverse kinematics， which limits their space applications. In addition， traditional grippers require millimeter level or higher accuracy to capture targets with a point grasping interface，significantly increasing the requirements for manipulator control accuracy. Additionally，rigid grippers will inevitably cause collisions. Therefore， it is necessary to design a flexible end-effector that is not sensitive to pose accuracy.

Detumbling control is carried out after a robot arm captures a target. In-depth research has been conducted on combined spacecraft detumbling， with the majority of scholars focusing on issues such as uncertain target mass parameters，inaccurate dynamic modeling， and unknown combined spacecraft angular momentum. Zhang et al.introduced a coordinated stabilization scenario for unloading the unknown angular momentum of a combined spacecraft. A modified adaptive sliding mode control algorithm was proposed to reduce the unknown target angular momentum， where sign function and time-delay estimation were adopted to ensure the convergence speed and convergence performance of the system. Wang et al.designed an integrated control strategy for uncertain mass properties and unknown combined spacecraft angular momentum problems， including a detumbling strategy， coordinated control， and parameter identification.A seven-degree-of-freedom redundant space manipulator was used to verify the effectiveness of the control algorithm. Wei et al.adopted the prescribed performance control method for dynamic model uncertainty and actuator saturation. This type of controller does not rely on the system dynamic model，nor does it require inertial parameters identification， which dramatically decreases the complexity and difficulty of the controller design. All of the above methods can realize spacecraft detumbling.However，zero angular velocity as a direct control objective will inevitably lead to actuator saturation， and an excessive detumbling torque will also affect the stability of the chaser-target closed-chain system.

In summary， in the existing research on debris capture and detumbling methods，the target is usually considered to have a specific capture point or structure，which is not in line with the actual space debris situation.Moreover， zero angular velocity as a direct control objective will inevitably lead to actuator saturation. In this paper， a compliant capture and smooth detumbling strategy is proposed. Firstly， compliant clamping control is adopted to grasp a target without docking interface stability， where the target information， force sensor and inverse kinematics are not required. Secondly， an adaptive backstepping-based prescribed trajectory tracking control(PTTC) method is proposed to detumble the combined spacecraft in the presence of model uncertainties and nonlinearities.Finally， numerical simulations are carried out to validate the feasibility of the proposed capture and detumbling control method.

The remainder of the paper is organized as follows.In Section 2，we discuss the constraint analysis of a chaser-target system and establish a combined spacecraft system model in terms of the modified Rodrigues parameter. The controller design，including a capture controller and a detumbling controller，are presented in Section 3， numerical simulations and discussions are presented in Section 4， and finally， conclusions are provided in Section 5.

2. Constraint analysis and dynamic model

In this section， the constraints between two manipulators and a grasped target are considered， and the capture dynamic model and the detumbling dynamic model are derived. The space robot is assumed to consist of a service spacecraft with thrusters，two rigid space manipulators，and two semispherical claws as end-effectors.The target is rigid with a cylinder shape，as shown in Fig. 1.

For convenience， in the capturing and detumbling model，relative frames are introduced， as shown in Fig. 2. Point O denotes the origin of the space robot coordinate Oxyz fixed at the centroid of the space robot. Similarly， Odenotes the origin of the target coordinate OXYZ，and Odenotes the origin of the inertia coordinate.

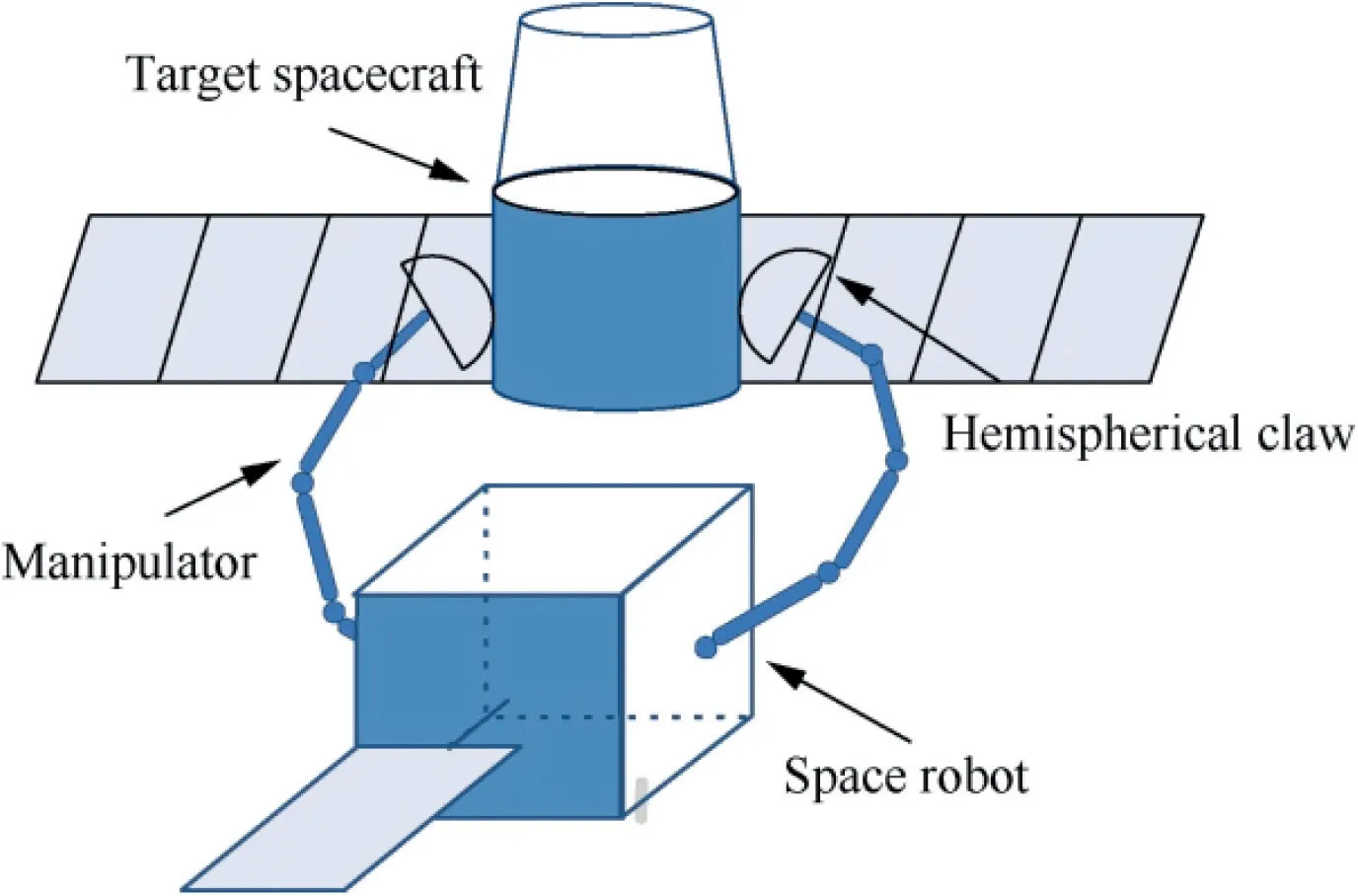
Fig. 1 Space robot capture an target with arbitrary shape.

2.1. Constraint analysis

It is assumed that the space robot and the target are on the same orbital plane， and they have the same angular velocity.The feasibility of this assumption has been confirmed by theoretical analysis and ground experiments.Thus，space target capture is simplified to the two-dimensional plane as shown in Fig. 2.

The position of the target centroid is denoted by Owith the coordinates （x，y） expressed in the space robot frame. Let the number of ith joint be N（i ＝1，2）(i ＝1 represents the left manipulator， and i ＝2 represents the right manipulator). The center of the hemispherical claw is located at the end of the manipulator， which is defined as O（x，y） and O（x，y）. According to the manipulator kinematics， the two points can be expressed as

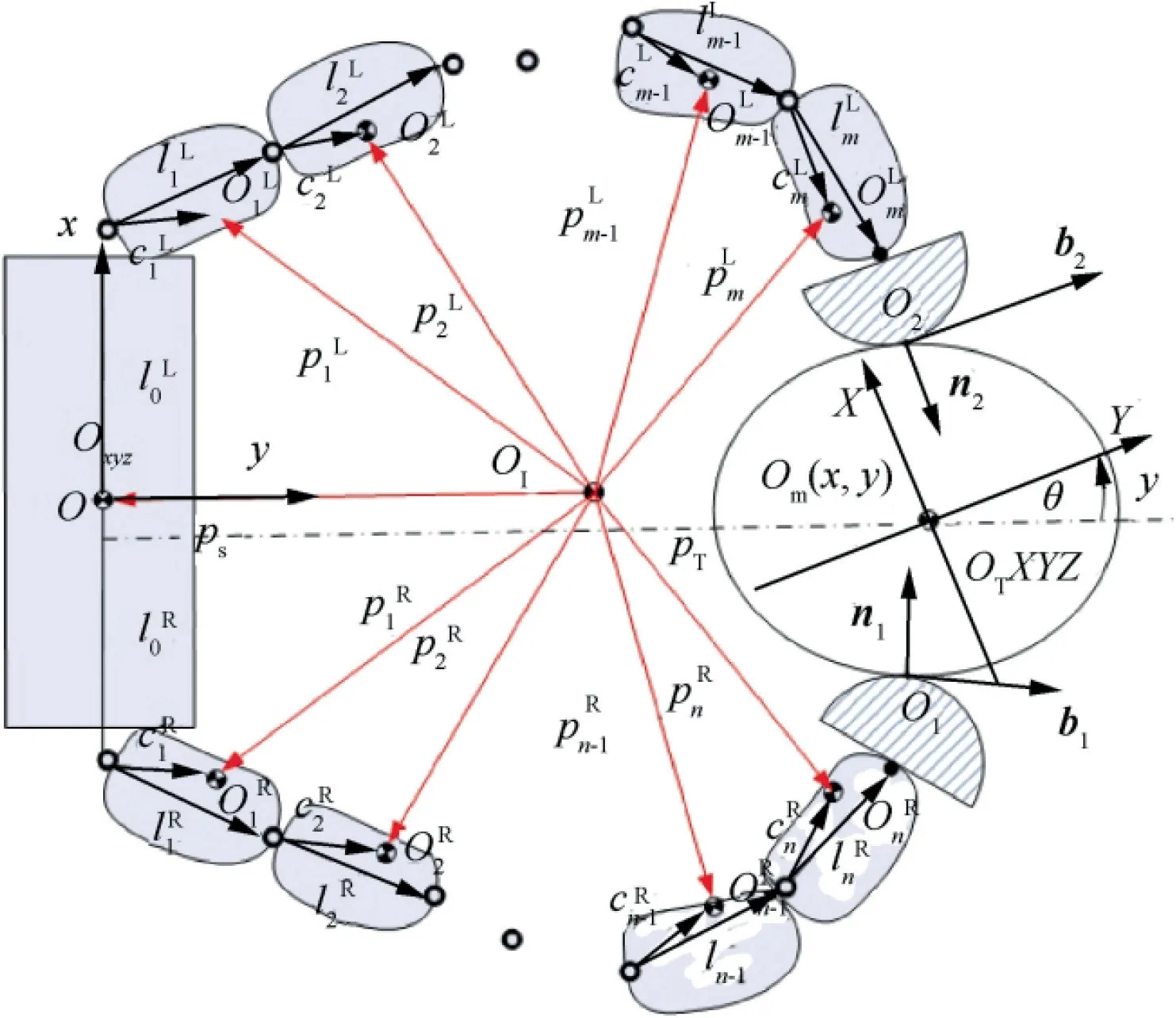
Fig. 2 Frame of chaser-target assembly.

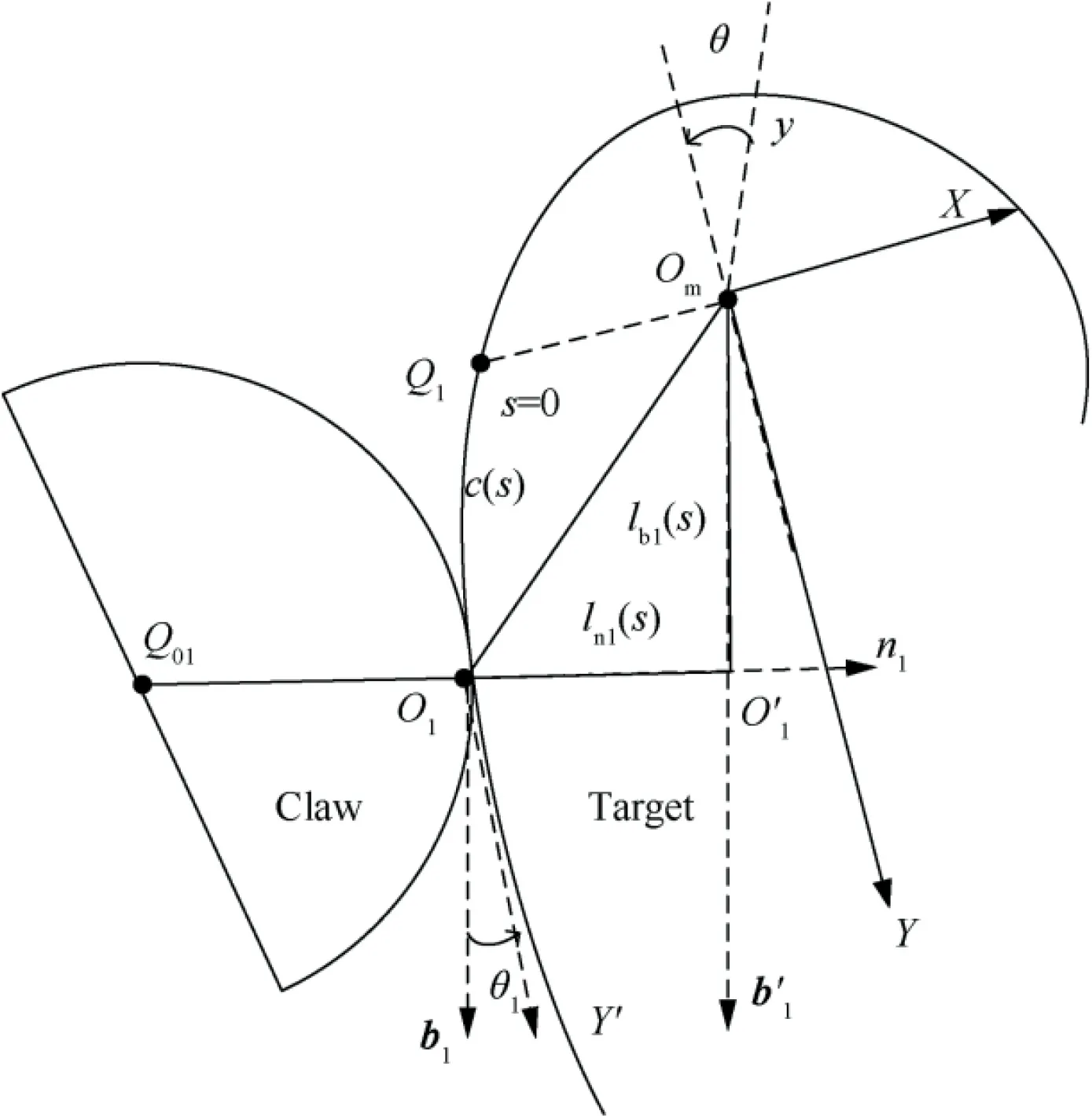
Fig. 3 Geometrical relationship between claw and target.

2.2. Capture dynamic model

By introducing Lagrange’s multipliers fand λ，corresponding to holonomic constraints Q＝0 and nonholonomic constraints R＝0 for i ＝1，2， we have

2.3. Detumbling dynamic model

After the target is captured by the space robot， a combined spacecraft is formed in the post-capture phases. Hence， combined spacecraft detumbling can be achieved through the space robot attitude stabilization system， and the detumbling dynamics equation must first be established.To avoid geometric singularity，the kinematic model of the combined spacecraft in terms of the modified Rodrigues parameter (MRP) can be expressed as

where Tis the control torque， Tis the disturbances torque，ωis the skew-symmetry matrix of ω， and I is the inertia tensor of the combined spacecraft. Although the inertial parameters of the combined spacecraft can be obtained through the parameter identification method， accurate identification is difficult.Therefore，the inertia uncertainty must be considered，so that the dynamic equation containing the inertia uncertainty can be derived as follows

3. Controller design and stability analysis

In this section， capture controller and detumbling controller are designed to capture and stabilize the tumbling debris.The space manipulators are controlled by the capture controller to grasp the debris. Once stable grasping is achieved，the space robot and the debris form a combined spacecraft in the post-capture phase.Consequently，the target detumbling problem is transformed into a combined spacecraft attitude stability problem，which can be solved by controlling the space robot thrusters.

3.1. Force/torque balance conditions

As shown in Fig.3， the pressing force emerging at the contact point Ois defined as f， and the opposite pressing force emerging at the contact Ois defined as f. According to the closed-chain constraint relationship， the torque generated by facts on Oand the torque generated by facts on O. The total torques around the z axis can then be expressed as

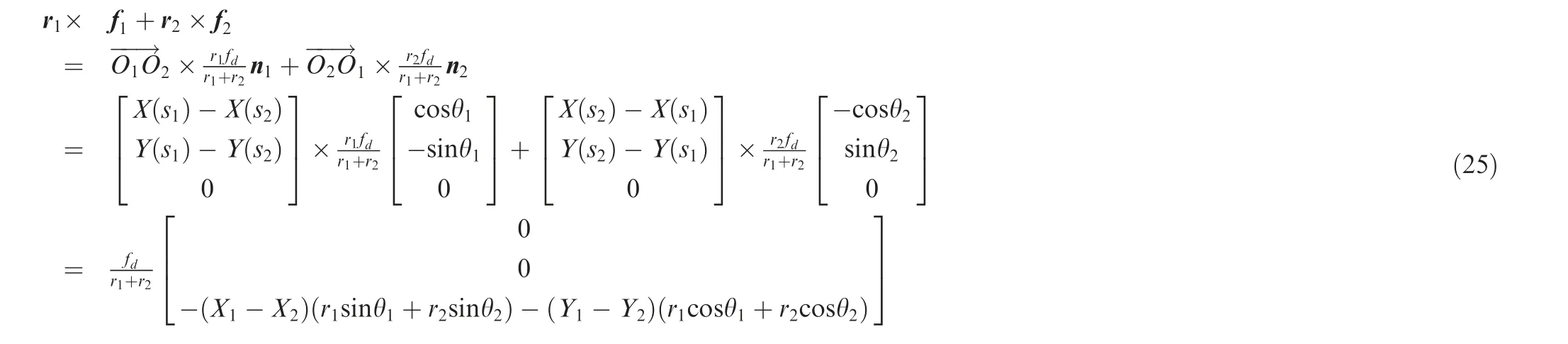
To summarize， it is possible to adjust s by controlling the manipulators to meet the target equilibrium condition and achieve stable capture.

3.2. Capture controller design

It is difficult to grasp debris with an arbitrary shape because the surface of the debris is changeable and the mass parameters are unknown. Inspired by the movements of a human hand grasping an object and referring to the feedback control method，a control input named ‘‘compliant clamping” is adopted， and a hemispherical claw is designed to achieve the force/torque balance by adjusting the manipulator joint angles，which is given by

where V＝K ＋U ＞0.

Therefore， the closed-loop system satisfies passivity. If the system is equal-constrained， then the quantity Vbecomes a Lyapunov function， and ˙q， ˙z converge to zero as t tends to infinity. According to LaSalle’s invariance theorem， we have f＝f＝f.The capture controller structure is shown in Fig.4.

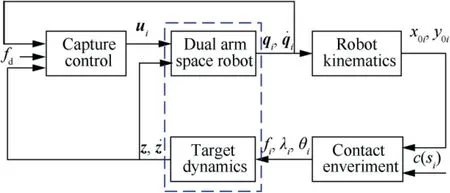
Fig. 4 Schematic diagram of capture control system structure.

3.3. Detumbling controller design

The combined spacecraft is formed in the post-capture phase，but it is not fixed.To prevent the target escaping from the claw due to sliding， an adaptive backstepping-based prescribed trajectory tracking control is proposed to reduce the maximum detumbling torque， save the propellant， and ensure the smoothness of the detumbling process.

3.3.1. Adaptive backstepping control

The original tracking errors are defined as

Step 2: The quadratic form is chosen as a Lyapunov function

Remark 1. If the control signal output is unsaturated， the compensated tracking errors ηand ηwill converge to the original tracking errors zand z.Otherwise，if the control signal output is saturated， even though zand zmay increase， ηand ηcan still converge to zero. Moreover， the adaptive parameter estimation remains stable as it is updated by the compensated tracking errors.

The thrusters are used as the attitude stabilizing actuator of the combined spacecraft.The optimal control allocation problem can be described as follows:

3.3.2. Prescribed trajectory of combined spacecraft detumbling

By presetting the detumbling trajectory of the combined spacecraft， the detumbling time and angular velocity are prescribed so as to avoid the excessive controller output and actuator saturation caused by simply controlling angular velocity. Specifically， this section applies an intelligent algorithm to optimize the trajectory of the combined spacecraft， including attitude trajectory and angular velocity trajectory.

First， the initial and desired state constraints for trajectory planning are introduced， including the attitude angle， angular velocity， and angular acceleration of the combined spacecraft at the initial time tand the end time t， which satisfy the following constraints:

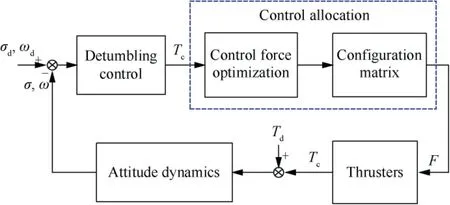
Fig. 5 Schematic diagram of detumbling control system structure.

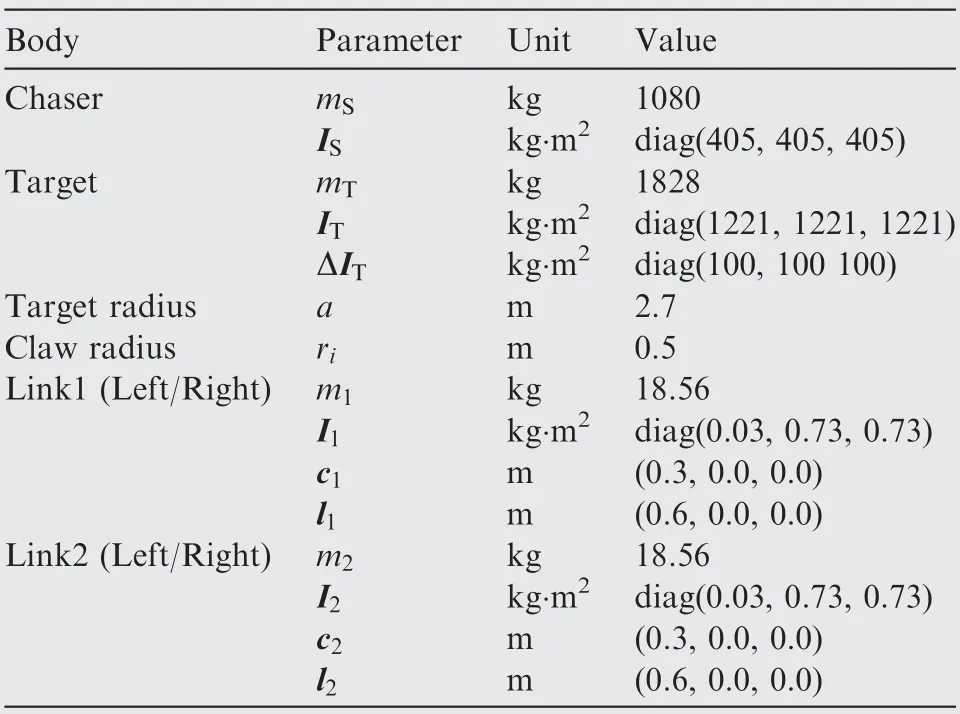
Table 1 Physical parameters of space robot and target.

4. Numerical simulations

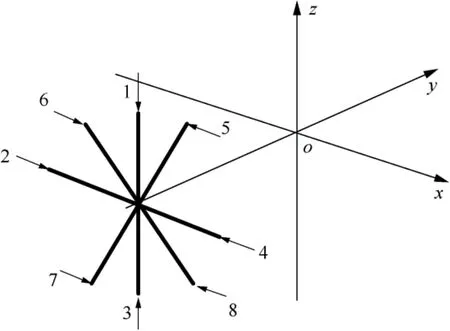
Fig. 6 Configuration of thrusters in space robot body frame.

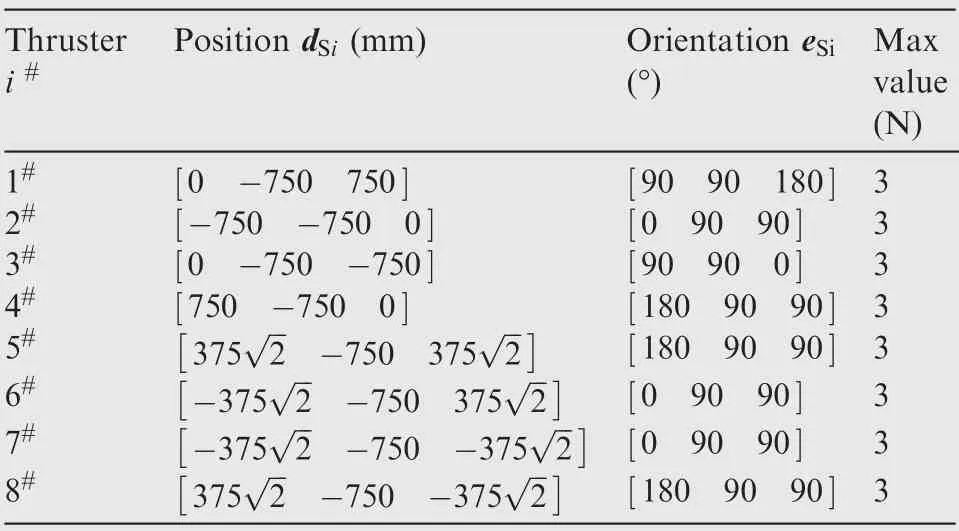
Table 2 Mounted positions and vectors of thrusters.

Fig.7 shows the dual-arm clamping force curve.The simulation results show that accurate grasping force control is still achieved without the contact force sensor. Moreover， due to the use of elastic claws， no impact caused by collision appears in the capture process，and the capture process is smooth.The tangential force compensation is shown in Fig.8.To satisfy the force/torque equilibrium condition，the control item G（t ）generates a tangential force compensation to prevent the rolling motion， which is effective for grasping an arbitrary shape target.Fig.9 and Fig.10 show the target pose adjustment during the capture process. The simulation results show that under the condition of the initial capture position asymmetric， by adjusting the posture of the claw，the adjustment of the capture position is completed， and force/torque balance is achieved，ensuring the stability of the target.

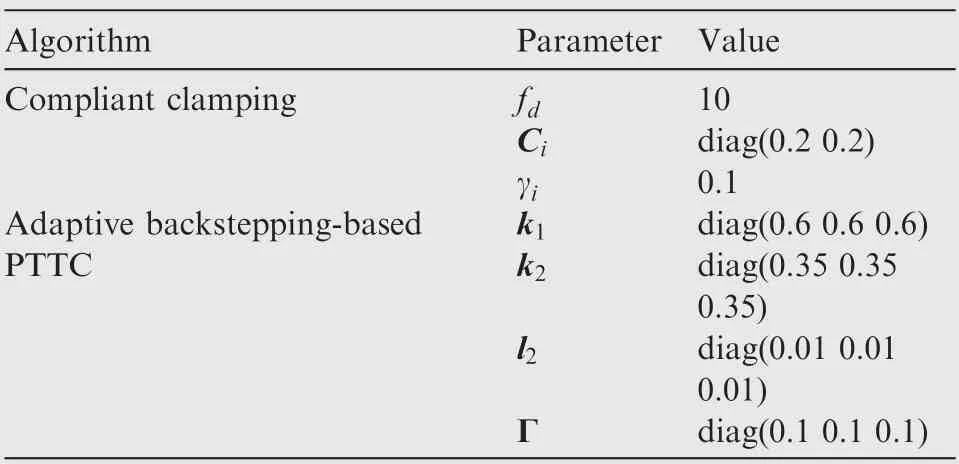
Table 3 Control parameters.

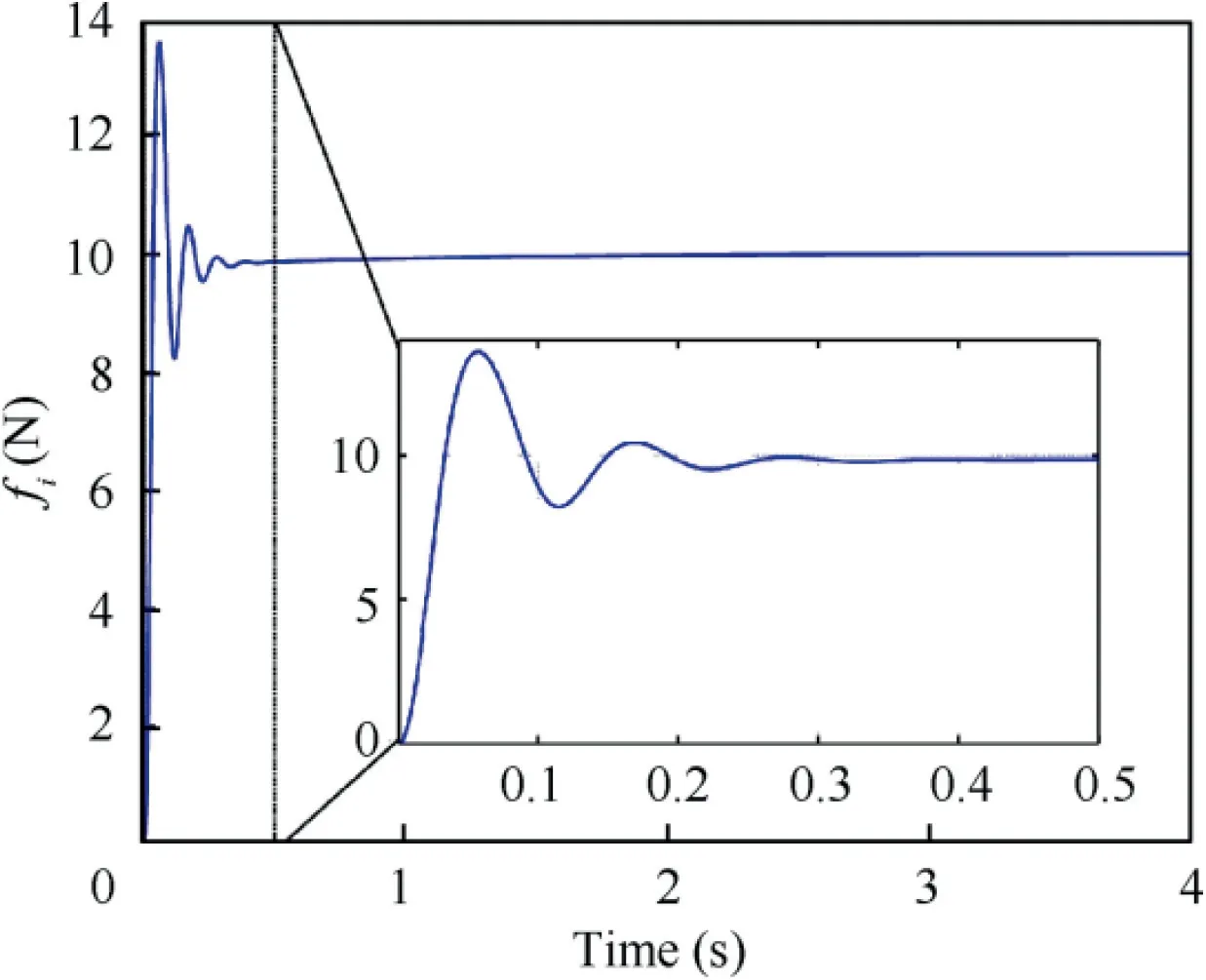
Fig. 7 Trajectory of normal force.

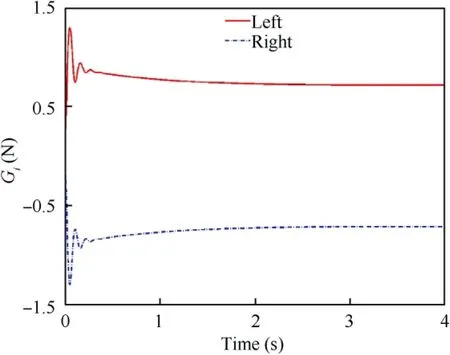
Fig. 8 Trajectory of tangential force compensation.

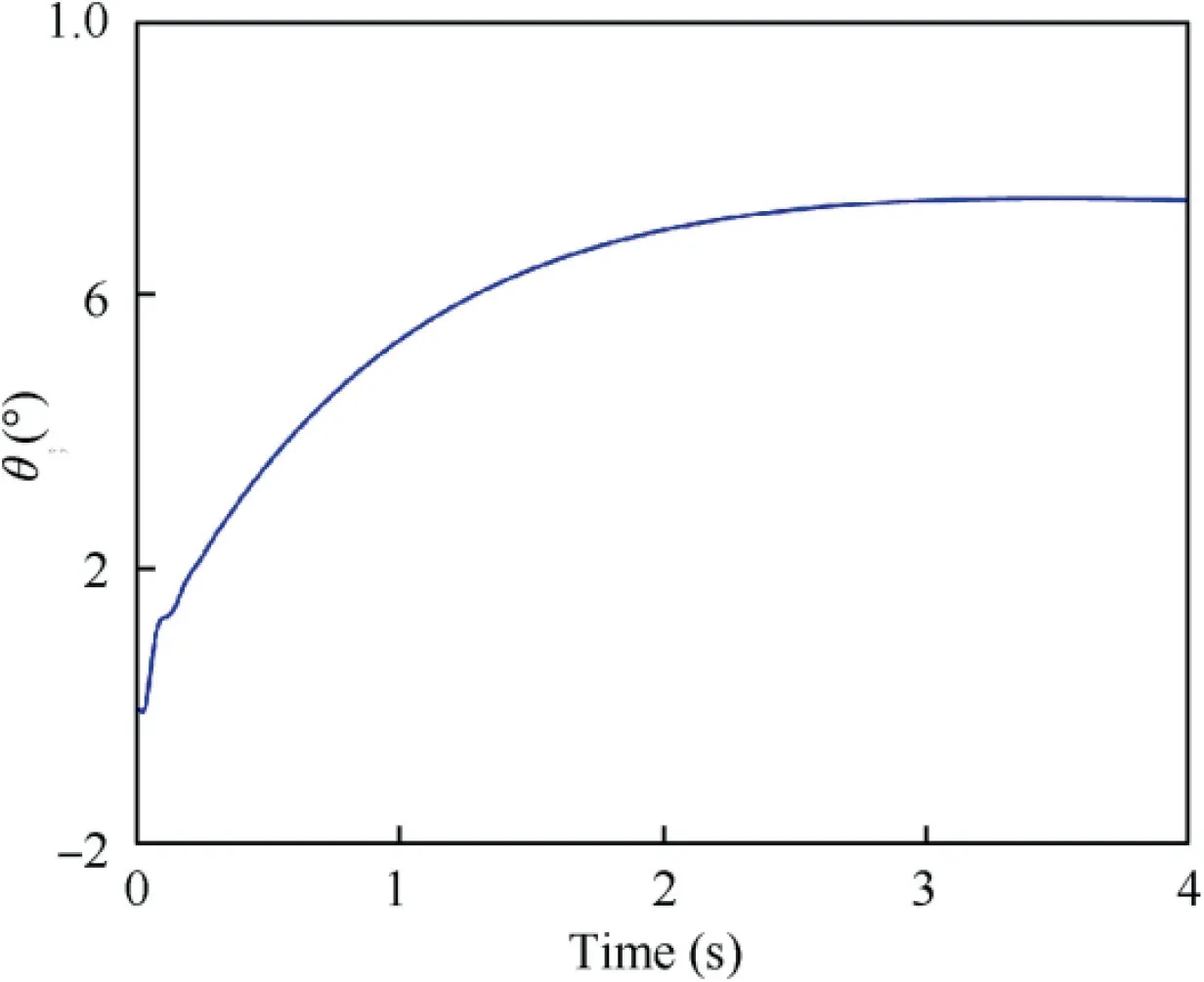
Fig. 9 Trajectory of target orientation angle.

Fig.11 and Fig.12 show the state of the robotic arm during the capture process. The simulation results show that the control torque is continuous， and the joint angles are smooth，which ensures the engineering feasibility of the controller.Moreover， compared with traditional force/position control，compliant clamping control does not require the solving of manipulator inverse kinematics， thus avoiding a large number of calculations and possible kinematic singularities.

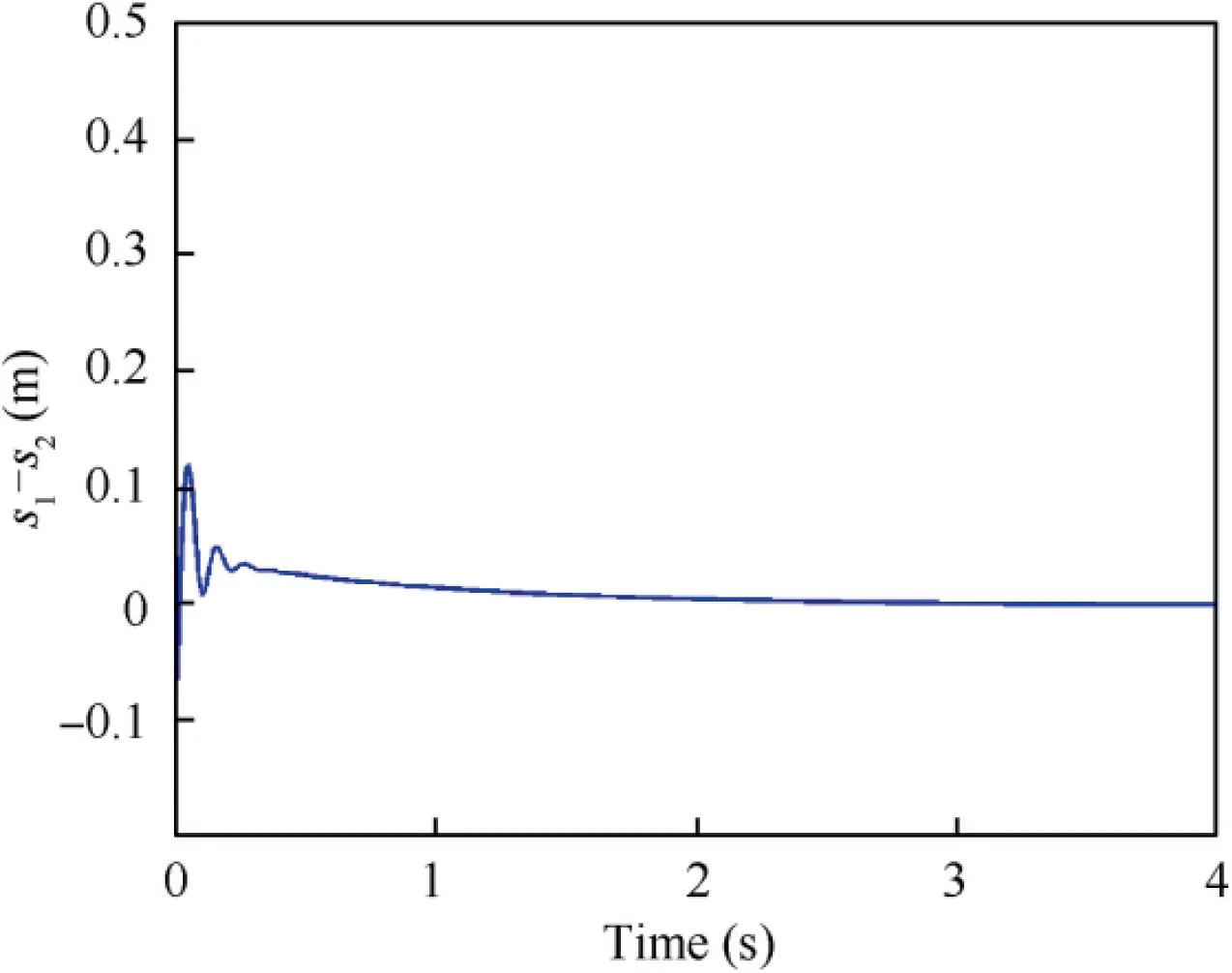
Fig. 10 Trajectory of arc length deviation.

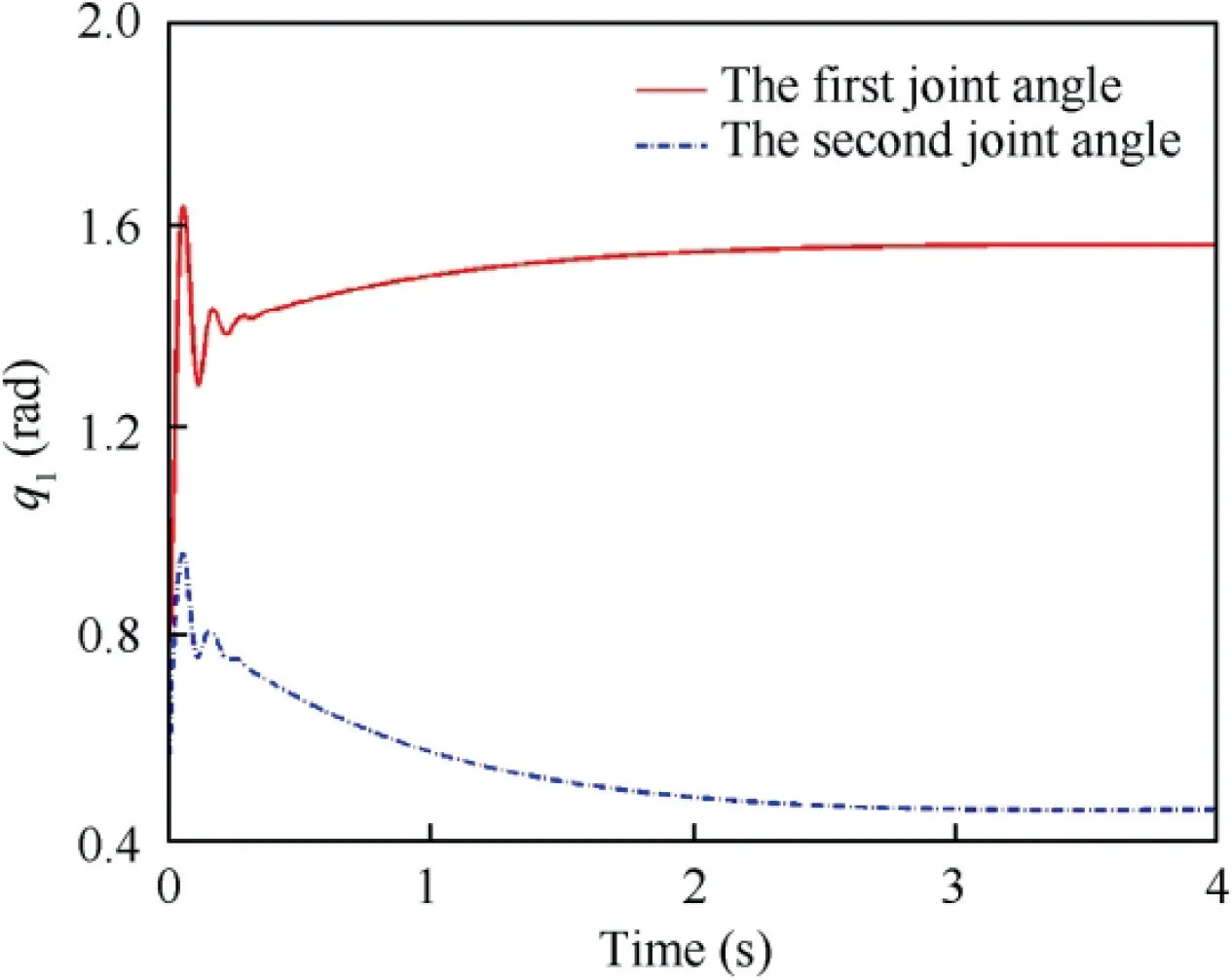
Fig. 11 Trajectory of joint angular.

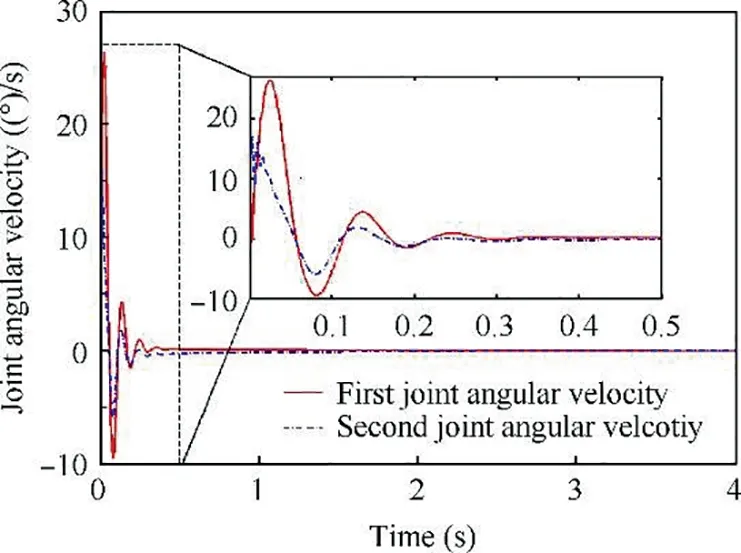
Fig. 12 Trajectory of joint angular velocity.

The space robot and the target constitute the combined spacecraft in the post-capture phase. Therefore， the target’s detumbling mission is transformed to combined spacecraft detumbling.Because the target itself does not have an attitude control ability，it is necessary to complete the combined spacecraft detumbling through the space robot attitude control system.

Fig. 13 Coefficient optimization through the PSO algorithm.

Fig. 14 Trajectory of combined spacecraft attitude.

Fig. 15 Trajectory of attitude tracking errors.

Fig. 16 Trajectory of combined spacecraft detumbling.

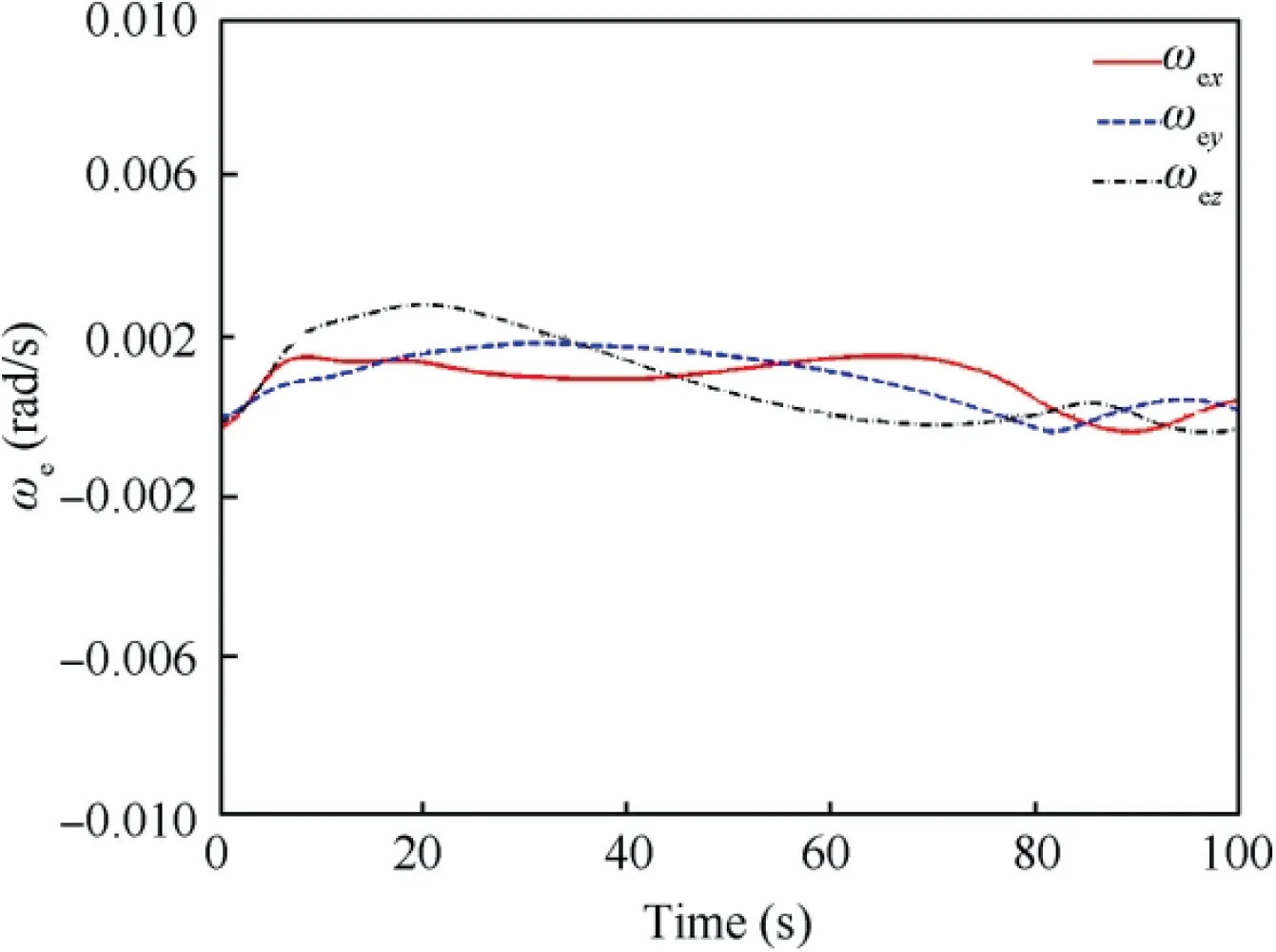
Fig. 17 Trajectory of angular velocity tracking errors.

Fig. 18 Detumbling control torques after optimization.

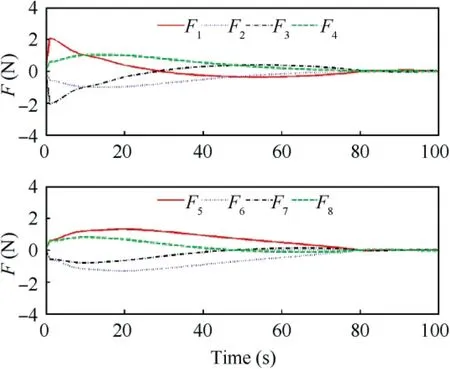
Fig. 19 Thrust curves after optimization.

Adaptive backstepping-based PTTC was adopted to track the optimized detumbling trajectory.Fig.14 and Fig.15 show the combined spacecraft attitude adjustment trajectory and attitude tracking deviation， where the simulation results show that the combined spacecraft remains stable after the detumbling is achieved. Fig. 16 and Fig. 17 shows the combined spacecraft detumbling curve and angular velocity tracking deviation， respectively. The simulation results show that the angular velocity deviation finally converges to zero within the 80 s and stable detumbling is finished. Note that a small error remains in the attitude adjustment trajectory， which is caused by the continuous disturbance torque added in the simulation.

The control torque output curve are shown in Fig. 18， and the thrust curves after optimization generated by the control allocation module are shown in Fig. 19. The optimized maximum output torque of the actuator is adjusted to within 4 N， which effectively avoids actuator saturation， and maintains output smoothness.

Due to the limited propellant carried by the space robot，propellant consumption is one of the main constraints to be considered in space missions. Under the conditions that the combined spacecraft configuration and the actuator installation position remain fixed， adjusting the angular velocity trajectory can save the total propellant consumption. The thrust produced can be calculated by multiplying the mass flow rate of the propellants by their exhaust velocity relative to the engine as

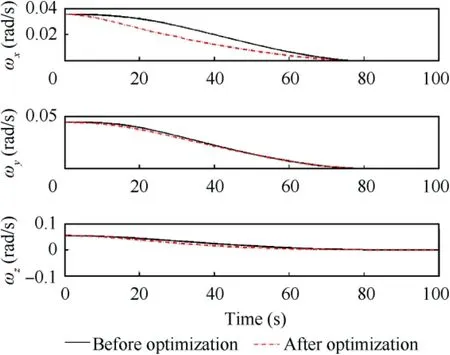
Fig. 20 Comparison of detumbling trajectory before and after optimization.

Fig. 21 Comparison of propellant consumptions.

where Fis the thrust obtained from the ith engine， gis the standard gravity， Iis the specific impulse， and ˙mis the mass flow rate of the expended propellant.

Considering that gand Iare constants， let Jbe the propellant consumption index， obtaining

The detumbling trajectory is then compared with existing literature， and the optimized trajectory is shown in Fig. 20.Using trajectory optimization， the thruster propellant consumption is saved as shown in Fig.21.As can be seen，the propellant consumption index before optimization is 511.8708，while the index after optimization is 388.4243. Therefore， the propellant consumption is reduced by 24.11% after optimization，which effectively improves the space manipulation ability of the space robot.

5. Conclusions

This paper presented a control strategy for stable grasping and smooth detumbling of a space object without a specific grasping point， and an elastic hemispherical claw was adopted.Unlike the previously studied fixed connection capture methods， this capture strategy employed a closed-chain structure to clamp the target. The capture control could achieve force/-position adjustment without force sensor and object information， and target slipping was avoided through prescribed trajectory tracking control in the detumbling phase.The effectiveness of the control strategy was demonstrated by numerical simulation， which indicated that the proposed method also avoided actuator and reduced propellant consumption. This research overcomes the limitation that non-cooperative target capture is only for objects with specific grasping points. The main contributions are as follows:

(1) An elastic hemispherical claw is explored to achieve compliant capture，which does not incur discontinuous contact force， and facilitates contact position adjustment.

(2) Compliant clamping capture control is adopted， which does not require any force sensor or target information or the solving of inverse kinematics.

(3) An adaptive backstepping-based PTTC is proposed by adding an intelligent algorithm to the controller design， and a remarkable effect of propellant saving is obtained.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgement

This study was supported by the National Natural Science Foundation of China (Nos. 61725303 and 61803312).