螺旋桨脉动压力作用下自航船舶艉部振动数值研究

工作在船后非均匀尾流场中的螺旋桨承受周期性的变化力，其诱导的压力场传递到船体表面产生脉动压力，即螺旋桨表面力，是引起艉部结构振动的主要原因.船体振动关系到船舶的乘用舒适性，影响船上机器和设备的正常工作，严重时对结构产生疲劳破坏.振动辐射噪声不仅会破坏军用舰艇的隐蔽性，也会对海洋动物的生活环境产生干扰.因此，开展螺旋桨激励下船艉结构振动机理分析与减振措施研究具有重要的工程意义.

近年来，研究人员针对螺旋桨脉动压力引起的船体振动问题开展了大量研究.刘西安根据国家军用标准计算了螺旋桨叶频表面力，然后均匀施加于螺旋桨上方局部区域，探究了结构形式变化对振动响应的影响.陈翔等基于霍尔顿法计算了螺旋桨叶频脉动压力，比较了3种脉动压力加载方案下艉部与上层建筑振动响应的不同，采用模态叠加法实现了对该船的振动计算与评估.周清华等根据经验公式计算得到螺旋桨激励力，通过瞬态响应分析方法预报了滑行艇艉部结构振动响应.船舶航行时螺旋桨激励力的准确预报直接影响到艉部振动计算的可靠性，目前在船舶振动分析时，螺旋桨激励力大小通常根据经验公式得到，并且作用区域大多采用单点、多点或者某局部区域，这种加载方式与船体表面真实压力分布存在一定的差距，因此计算结果具有一定的局限性.

1214 Efficacy and safety of intravenous thrombolysis or bridging therapy for acute minor ischemic stroke with large artery occlusion

部分学者基于试验测量的压力数据计算船体振动响应，船体表面压力分布更加真实可靠，但是试验测量成本较高且周期长.许树浩等根据水槽试验得到螺旋桨诱导的船体表面力，完成了全船总振动计算.朱理等采用脉动压力试验数据，实现了不同航行工况下的舰船结构振动分析.随着计算流体力学(CFD)技术的日益成熟，越来越多的学者通过数值方法研究复杂流场中螺旋桨的激振力特性.陈如星等基于CFX软件分别将理论轴向伴流数据与船模试验伴流数据设置为计算域的速度入口边界条件，取代了船艉结构三维模型，预报了非均匀来流下的螺旋桨非定常水动力，为伴流场中螺旋桨激振力的计算提供了可行的数值方法.Yao等在获得船艉非均匀伴流的条件下，计算并分析了螺旋桨轴承力特性，探究了伴流场中横向速度对轴承力计算的影响.随着计算机性能的提升，很多学者开展了船桨一体的数值研究.进行船舶自航数值模拟可以考虑船桨的相互干扰以及伴流场中所有分量的影响，因此，将“船+桨”自航数值模拟应用于螺旋桨激励力预报，开展螺旋桨脉动压力下自航船舶艉部振动规律的研究是非常有必要且有实际意义的.结构振动响应受激励力与结构固有特性的共同影响，现有文献很少结合自航船舶艉部表面复杂的压力分布特性、结构固有特性以及结构振动响应开展系统的研究.

本文以3 500TEU集装箱船KCS的模型船为研究对象，开展船桨一体的自航数值模拟，获得了船舶自航时螺旋桨诱导的船体表面脉动压力.以此作为外激励，应用有限元-边界元相结合的方法计算艉部结构耦合模态以及振动响应，探究螺旋桨脉动压力特性、结构固有特性以及振动响应的对应关系，为自航船舶艉部振动的数值预报提供了可行方法.在此基础上，研究增加板厚与安装加强筋对艉部振动响应的影响规律.

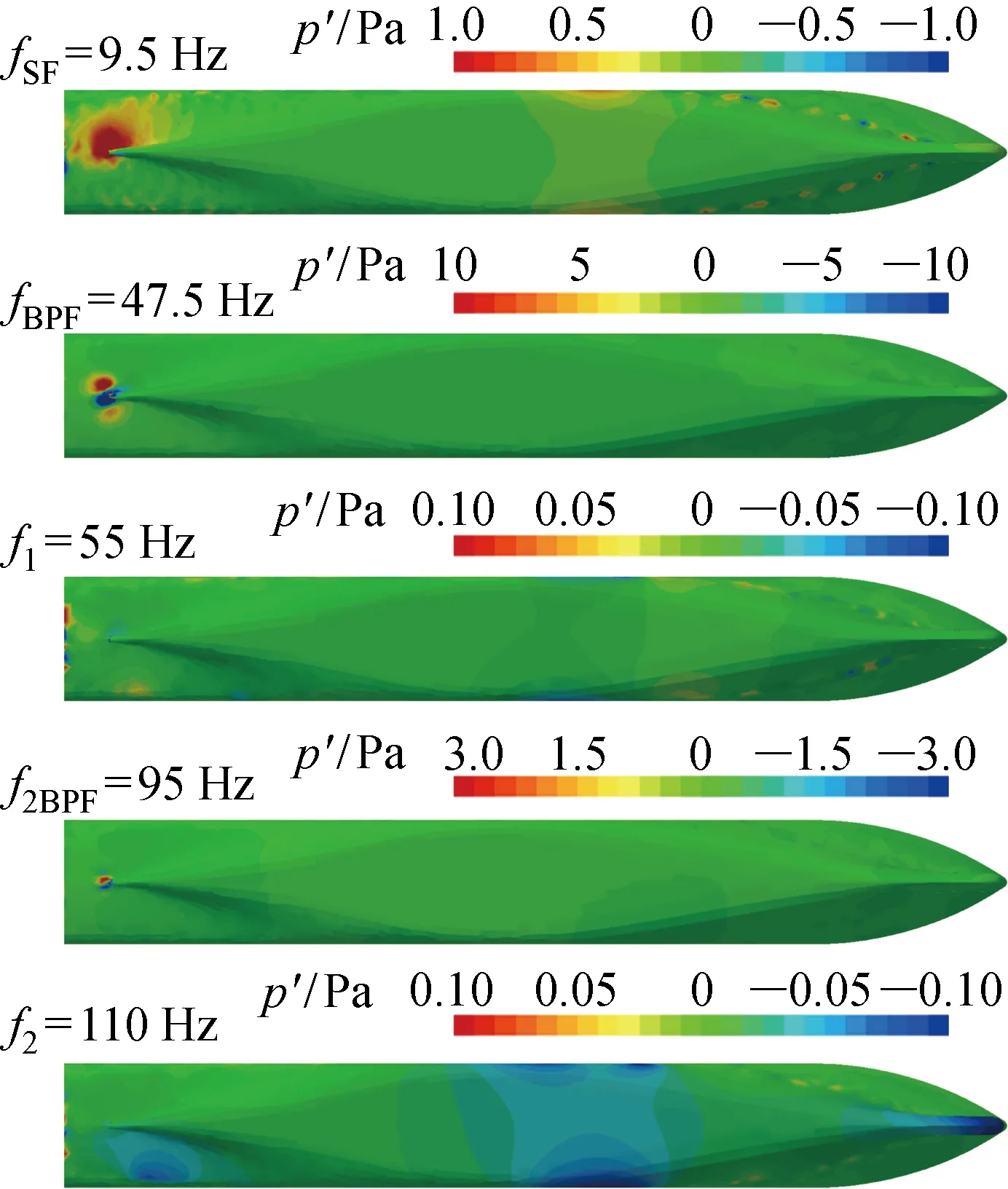
..船体表面脉动压力 船舶在航行时，表面压力随时间变化，变化的压力是结构产生振动的根本原因.在静水中(不考虑波浪)航行的船舶，船体表面压力的变化主要出现在船艉(螺旋桨上方区域).将船体表面脉动压力做频谱分析，图6所示为几个特征频率时的压力分布云图，其中′为压力幅值，定义螺旋桨轴频=9.5 Hz，定义螺旋桨叶频=47.5 Hz，螺旋桨倍叶频=95 Hz，另外选取=55 Hz 与=110 Hz的压力幅值分布做比较.可以看出，螺旋桨叶频是船体表面脉动压力的主要频率，该频率的压力幅值远大于其他频率的幅值.在其他频率分量中，倍叶频以及轴频的幅值比较明显.从轴频、叶频和倍叶频的压力云图可以看出，艉部表面的压力幅值往舷侧方向减小.右旋桨诱导的船体表面脉动压力不是左右对称的，右舷侧的压力幅值大于左舷侧的压力幅值，并且最大脉动压力位置出现在桨轴线右侧.

1 计算模型

1.1 螺旋桨表面力激励自航船舶艉部振动预报方法

考虑到艉部结构振动变形对周围流场的影响很小，在进行自航数值模拟时采取刚体假设，忽略结构振动对流场计算的反馈，即采用单向流固耦合方法计算外载荷对艉部结构的激励作用.另外，在船体振动计算时将艉部结构看作弹性体，需要计及舷外水对结构的耦合作用.本研究考虑流体可压缩性，基于结构有限元耦合流体边界元理论处理流固耦合问题，计算流程如图1所示.首先基于CFD进行静水中船桨自航数值模拟，得到螺旋桨诱导船体表面脉动压力分布，并保存每个时间步内的压力信息，作为后续振动计算的外载荷输入.然后，分别建立艉部结构有限元模型与浸水部分边界元模型.采用有限元方法计算艉部模型的干模态，之后通过结构有限元模型耦合流场边界元模型，建立艉部结构及周围流场的声固耦合分析模型，可进一步计算湿模态.最后，以船体表面脉动压力为外载荷，基于模态叠加法进行声固耦合分析，计算艉部结构振动响应.

或许是下午喝了点茶的缘故，晚上久久不能入眠，我索性翻看手机，却无意进入露露的QQ空间。空间里的一条说说引起了我的注意：“值得纪念的一天，闺蜜小雨、好友梓轩，成功表白！”

11月12日晚，位于迪庆德钦的灾民安置点灯火通明，“没想到一入住安置点灯就亮了，有亮光就觉得有希望，心里也就踏实了。”夜幕下，提前转移至灾民安置点的群众脸上露出了温暖的笑容。迪庆供电局、丽江供电局早在堰塞湖形成之初，就主动靠上去，提前和当地政府联系，及时掌握安置点的动态变化情况同步开展供电接线工作，确保“搭建一顶帐篷，点亮一盏电灯”。

1.2 船桨自航模拟数值模型

以标准船模KCS及KP505螺旋桨为研究对象，几何模型与主尺度参数分别如图2与表1所示.

利用雷诺平均(RANS)方法模拟船舶自航时的黏性湍流场，为了使RANS方程组封闭，引入剪切应力输运(SST)-湍流模型.该模型利用混合函数在近壁区使用准确性高的-模型求解，在远场应用具有自由流独立性的-改进模型，可以更可靠地模拟逆压梯度流动问题.SST-模型中湍流黏性系数、湍流动能以及特定湍流耗散率的定义式为

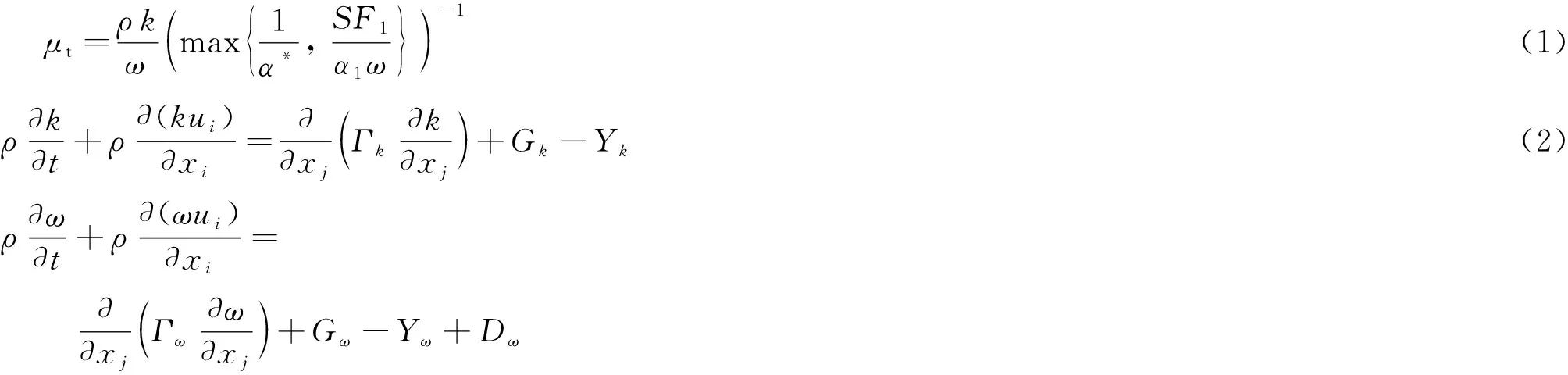
(3)

式中：为流体的密度；为湍流动能；为特定湍流耗散率；为流体微团的平均剪切应变率；为混合函数，表示-模型与-模型的混合使用情况；与为模型常量；为时间；与为笛卡尔坐标；为流体速度在坐标轴(=1, 2, 3)上的分量；与为扩散率；为湍动能的源项，表示由流场中的平均速度梯度产生的湍动能；与为扩散项；为耗散率的产生项；为交叉扩散项.

2.2.3 CGF促进牙髓组织基础研究 国内学者杜楠[27]通过培养人牙髓干细胞，将不同浓度CGF作用于干细胞，通过检测碱性磷酸酶浓度作为分析CGF对牙髓干细胞增殖分化的影响，结果显示，碱性磷酸酶浓度增加，并和CGF浓度呈正相关，得出结论：CGF在一定浓度下可以促进牙髓干细胞的增殖分化。

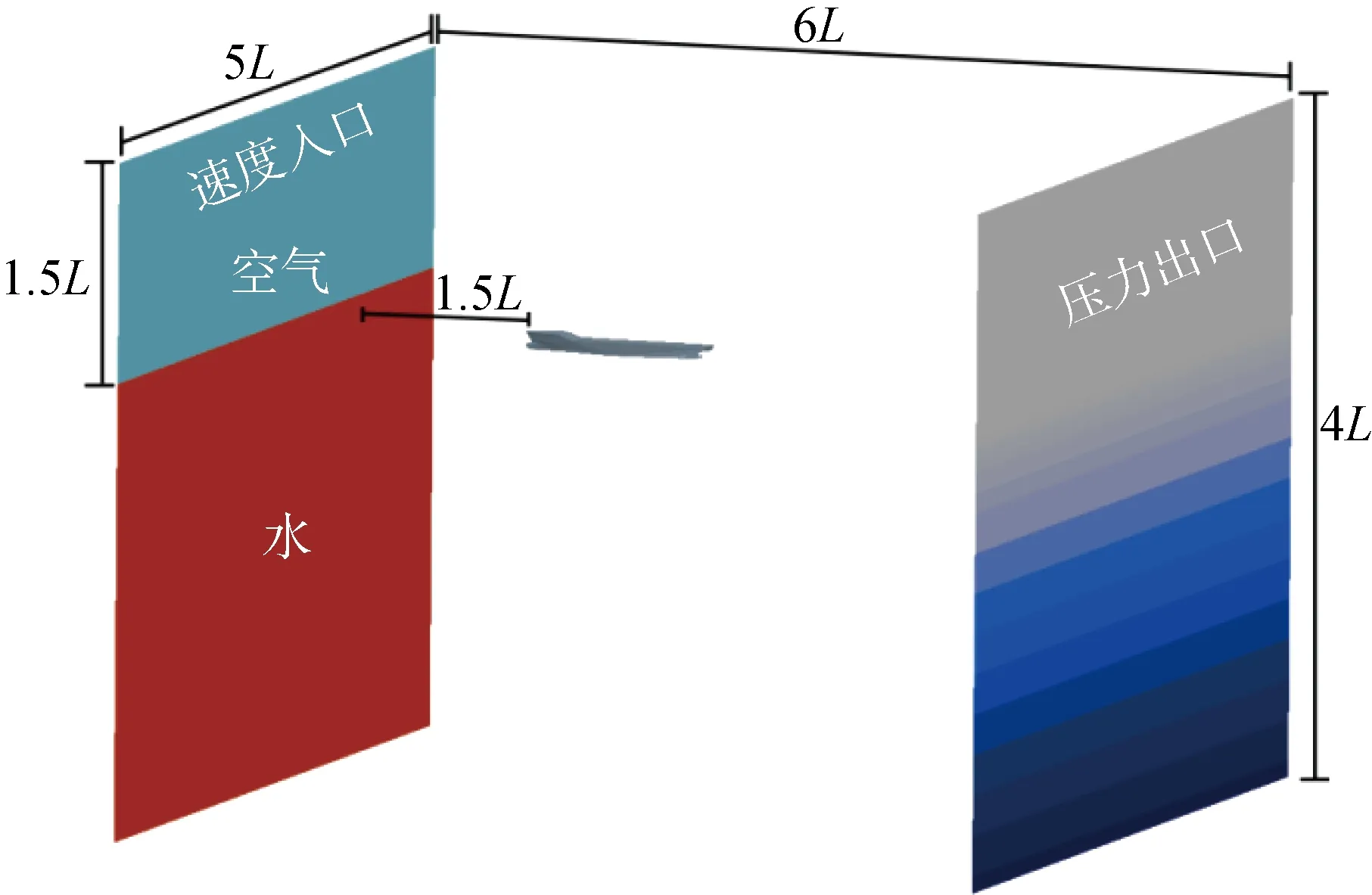
建立船桨自航数值模拟的计算域，如图3所示，图中为船长.船模上游入口边界设置为速度入口，来流速度为 2.196 4 m/s；船模下游出口边界设置为压力出口，计算域顶部、底部及侧面边界均设置为滑移壁面.采用流体体积(VOF)模型求解水与空气的交界面，计算自由液面处的船行波.为避免计算域边界反射波对自由液面产生干扰，侧面边界与压力出口均采用波阻尼函数进行消波处理.

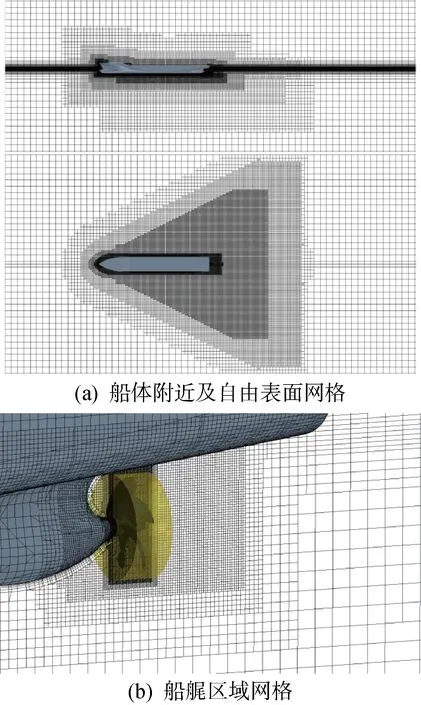
采用切割体网格对计算域离散.如图4所示，为了捕捉复杂的船行波，采用多块结构对船体附近区域以及自由表面进行网格加密.计算域分为旋转域与静止域，采用滑移网格技术处理螺旋桨的旋转问题，旋转域与静止域交界面的网格尺寸要保持一致.为了准确模拟非均匀尾流场，在船艉区域进行多重网格细化.经过网格无关性验证，确定合理的网格数目为429万.

式中：为声固耦合矩阵；()为间接边界元影响矩阵；为结构表面压力差向量.

1.3 艉部结构振动计算模型

针对船体艉部结构振动问题，考虑到结构与流体的耦合作用，结构动力学方程为

(4)

式中：为系统谐振频率；为结构质量矩阵；i为虚数单位；为结构阻尼矩阵；为结构刚度矩阵；为结构节点位移向量；为结构所受外载荷向量，此处为螺旋桨诱导的脉动压力；为耦合面上流体介质作用在结构上的动压力向量.

“十一五”开始，我国以刚性约束手段对大气主要污染物实行总量控制，在全国范围内开展了SO2总量减排实践，“十二五”在SO2基础上增加了NOx减排指标，“十三五”已将大气环境质量改善目标作为减排考核中心[14]。而火电行业作为大气污染物的重点排放源，是总量控制重点监管的领域。2006年国家环保部颁布的《二氧化硫总量分配指导意见》中加强和规范了SO2总量分配的落实工作，按照区域和时段(《火电厂大气污染物排放标准》)划分，统一规定排放绩效值，将排放绩效引入电力行业的二氧化硫总量分配中，其中东部地区第Ⅲ时段机组SO2排放绩效为0.7 g/kWh，详见图1。

(5)

式中：=/为波数，为流体介质运动圆频率，为流体介质中的声速.

利用格林公式将流体域中的微分方程(5)转换为边界上的积分方程，可得流场内任一点的动压力：

将周围流场通过边界元格式离散，与结构有限元耦合求解，假定流体为无黏、无旋且做小扰动运动，并考虑流体可压缩性，此时流场中各点的压力满足Helmholtz方程：

(6)

式中：为场点；为源点；(,)为Helmholtz方程的格林函数；为振动结构的表面法向；为结构表面压力差，即双层势；为结构表面压力梯度差，即单层势；为振动结构表面.

将式(4)中用边界积分方程(6)的形式来表示，再根据结构表面声压或声压差与结构表面法向振动速度的关系，以及法向振动速度与结构表面振速及位移的关系，经过处理可以得到满足单层势=0的结构有限元耦合间接边界元的动力学方程如下：

(7)

船桨自航数值模拟求解时首先保持旋转域静止，时间步长设置为0.4 s.计算120 s后，当监测的船模阻力系数曲线稳定时，表明船模绕流场已充分发展.以此作为初始解，设定旋转域网格以 9.5 r/s 的速度绕桨轴旋转，调整时间步长为3×10s，每步对应螺旋桨转动 1° .等计算稳定后，保存每个时间步内的船体表面压力数据.

为探究板的厚度变化以及有无加强筋对结构振动响应的影响，将船艉结构模型分别设置为4种板厚：=4.0，4.5，5.0，5.5 mm，另外在板厚为4.0 mm与5.5 mm时安装加强筋，共6组计算模型.图11所示为安装加强筋的船艉结构有限元模型，加强筋等间距布置，采用板单元离散，其厚度与船壳板厚度一致.表4所示为6组计算模型的前10阶耦合模态固有频率.可以看出，各阶模态固有频率随着板厚的增加均有不同程度的增大.安装加强筋后，板厚为 4.0 mm 与 5.5 mm 的船艉结构各阶模态固有频率均有相应的增加.

图5所示为艉部结构有限元模型与浸水部分边界元模型.艉部模型是在自航模拟所采用的KCS船模基础上添加基本结构而得到，假设图中横剖面处为横舱壁，采取完全固定约束.横剖面到艉封板的距离为1.55 m，约为船长的1/5，材料设置为结构钢.由于可以把梁、杆等小构件的作用转换成等效质量加在板上，为简化计算，船壳板、横舱壁以及甲板平台上均未设置加强筋，使用板单元离散.最终有限元网格总数为 14 769，边界元网格总数为 4 465.

2 计算结果

2.1 螺旋桨诱导船体表面脉动压力

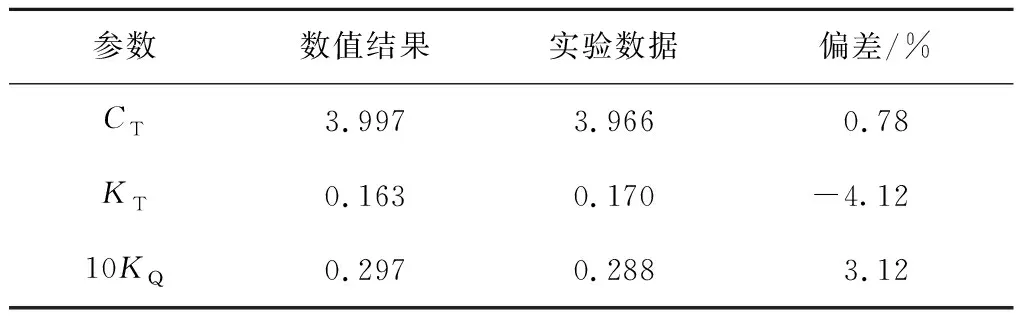
..船桨自航数值方法验证 将自航数值模拟得到的船舶阻力系数()、螺旋桨水动力性能参数(，10)与实验数据作对比，其中为螺旋桨推力系数，为螺旋桨扭矩系数.如表2所示，数值计算的船舶阻力系数与实验数据很接近，螺旋桨水动力性能与实验值的偏差在4.12%以内，由此可以证明船桨自航数值模拟的准确性.

式(1)中TFEA为回波信号起始点到特征点的时间,与回波信号起始点相差n个周期,而回波信号的周期由换能器B的中心频率决定。当每次测量特征点D2均在回波信号的同一位置时TFEA为常量,根据式(1)可以得到渡越时间TAB:

在船艉外底板表面布置6个监测点，如图7所示，图中监测点等间距分布，表示螺旋桨直径.点位于螺旋桨正上方、船舶中纵剖面内，点位于桨盘面下游，点与点位于右舷侧.图8所示为各个监测点的压力时域变化曲线，其中螺旋桨正上方的点压力幅值最大；点与点位于桨盘面内，右旋桨带动水流冲击导致点压力大于点压力；点与点位于桨盘面上游，压力波动幅值大致相等，压力变化存在一定的相位差.

选取点与点，将压力时域数据做快速傅里叶变换，结果如图9所示，为功率谱密度，为频率点与点的脉动压力最大幅值出现在螺旋桨叶频，点在螺旋桨倍叶频也有峰值出现，其他频率分量几乎为0.

The teacher gives the students different tasks according to their interests,levels,need and strategies.So the students can improve in the field they like.With the development of their language skills and competence,they can be encouraged to enlarge their interestsand need.

2.2 艉部结构振动响应

板厚为4.0 mm时艉部结构前10阶干模态与耦合模态的固有频率如表3所示.相比于干模态，耦合模态的各阶固有频率都有较大程度的降低，这是因为舷外水对结构振动的影响主要表现为附加质量，从而降低了其振动固有频率.在基于模态叠加法进行声固耦合分析时，应该采用干模态，否则会重复考虑流体耦合的影响.

振动位移监测点的分布同图7所示，与压力监测点一致.板厚为4.0 mm时6个监测点的振动位移的频谱分析结果如图10所示，图中′为振动位移.首先，各点的振动位移曲线最大峰值频率均出现在47 Hz处，该频率与螺旋桨叶频(47.5 Hz)很接近，由上节脉动压力的频谱特性分析可知，船艉外板受到的激励主要为螺旋桨叶频分量(47.5 Hz).并且结构的第1阶耦合模态固有频率为46.8 Hz，几乎等于螺旋桨叶频(47.5 Hz)，此时结构会出现共振.因此振动响应中47 Hz的振动位移幅值最大是合理的，这说明本文计算方法是可信的.其次，点的振动位移响应与点的振动位移响应一致，幅值最大根据212节的压力数据结果，螺旋桨诱导的脉动压力主要集中在点，并且右舷监测点的压力幅值高于左舷监测点，但是点的振动响应最小，点的振动响应与点的振动响应一致.这说明复杂结构的振动响应不仅受外激励的影响， 且与结构特性相关.

3 结构变化对振动响应的影响

移入场的被动接受还是主动选择，是影响很多作家地域书写的一个因素，对于主观型诗人陆游而言，这点尤为重要。而陆游在梁益地区的宦游生活，除了兴元府基本属于主动选择外，夔州以及成都、蜀州、嘉州各地都属于被动接受，因而他对梁、益二地书写的主要情调有明显的不同。上级任命的不可抗拒、个人生活命运的不可掌控，认命的被动无奈心态，让陆游的巴僰、蜀地书写以悲伤为主调。而兴元府，从地理位置上讲更属于“边州”，除军事地位比较重要外，其经济、文化各方面显然不如蜀，但陆游对其书写却显得热情高涨、兴高采烈。

螺旋桨激励力的主要分量为叶频与倍叶频，且叶频处压力幅值远大于倍叶频处压力幅值.在表4各阶模态固有频率中选取最接近螺旋桨叶频与倍叶频的固有频率值，计算错频比率，如表5所示.与原模型 I 相比，增加板厚与安装加强筋均可以引起结构固有频率远离螺旋桨叶频.另外，对于模型 IV 与模型V，虽然结构固有频率错开了螺旋桨叶频，但其某阶固有频率与螺旋桨倍叶频很接近.

保持船艉外板所受外激励不变，分别计算6组船艉结构模型的振动响应，取点的振动位移响应结果作比较，如图12所示.无加强筋的条件下，当板厚从4.0 mm增加到4.5 mm时，点的振动位移幅值明显降低.其主要原因是板厚为4.5 mm时，最接近脉动压力主频率(47.5 Hz)的是第1阶耦合模态固有频率(51.0 Hz)，从而避开了共振.当板厚从4.5 mm增加到5.0 mm时，点的振动位移幅值进一步降低.当板厚从5.0 mm增加到5.5 mm时，点的振动位移幅值又略有增大，且最大幅值所在频率为95.5 Hz.由表4及表5可知，该频率刚好为第5阶耦合模态固有频率，并且靠近螺旋桨倍叶频(95 Hz)，因此结构振动响应会出现明显峰值.此时的振动位移最大幅值与原模型 I 相比减小了 0.004 mm，不及模型 II 与模型 III 的减振效果明显.此外板厚为 4.0 mm 时，安装加强筋后，结构第1阶耦合模态固有频率增长为53.1 Hz，避开螺旋桨叶频 47.5 Hz，因此点的振动位移幅值明显降低.当板厚为5.5 mm时，安装加强筋后，结构耦合模态固有频率避开了螺旋桨倍叶频95 Hz，因此点的振动响应减弱.应当注意，当板厚增加为 5.5 mm 后，此时结构质量增加明显，因此在质量资源有限的情况下，应该选择适当的增加板厚(如模型 II 与模型 III)或者安装加强筋(如模型V).

图13所示为船艉结构振动位移在频域内=47.5 Hz 时的分布云图.首先，板厚为 4.0 mm、无加强筋时船艉结构振动响应最明显，原因是 47.5 Hz 接近该模型第1阶耦合模态固有频率.而其他各组计算模型的耦合模态固有频率均远离该频率，因此振动位移未出现较大幅值.其次，随着板厚的增加，该频率下的振动位移响应逐渐减弱，安装加强筋后同样如此.由此表明，增加板厚或者安装加强筋可以增大结构刚度，增强结构抵抗振动变形的能力，达到减振效果.

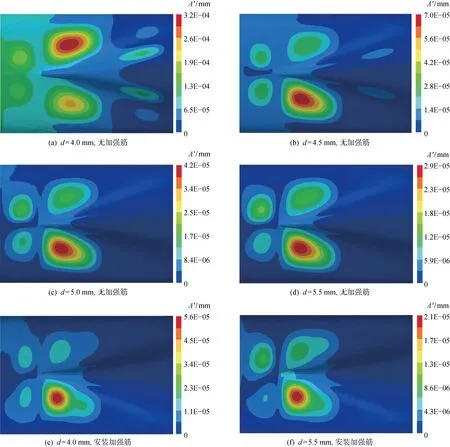
图14所示为船艉结构振动位移在频域内=95 Hz时的分布云图，由于激励力中螺旋桨倍叶频分量远小于其叶频分量，所以除了板厚为 5.5 mm、无加强筋时的振动幅值有所增加，该频率下的其他各组计算模型的振动位移幅值远小于叶频时的位移幅值.通常情况下结构振动最大位移对应的频率为螺旋桨叶频，只有当其他频率与结构某阶耦合模态固有频率一致时，才会有比较明显的振动位移出现.

4 结论

本文针对静水中航行的水面船舶艉部振动问题，通过船桨自航数值模拟获得了螺旋桨诱导船体表面脉动压力，分析了螺旋桨诱导船体表面脉动压力在时域与频域内的变化规律.建立了声固耦合分析模型进行艉部振动响应预报，研究了螺旋桨脉动压力特性、结构固有特性以及振动响应结果的对应关系.在此基础上，探究了相同激励作用下船艉结构变化对振动响应的影响，主要结论如下：

(1) 建立了螺旋桨激励自航船舶艉部振动的数值预报方法，船艉外载荷的加载方式更接近真实的压力分布，基于有限元-边界元法计算得到的结构振动结果更具有可靠性，该方法对于进一步研究船舶航行时的船体振动问题是有帮助的.

刘建说，本来我想让亲戚进大发的。夏俊答应了，但要六百块，说要打发总务经理和人事课长。分明是他自己想得好处，老子不想给他。而且我那亲戚刚出来，也实在拿不出钱来。

(2) 对于静水中航行的船舶，螺旋桨诱导的船体表面脉动压力中的叶频分量的幅值远大于其他频率分量的幅值；对于右旋桨，螺旋桨上方的右舷侧压力幅值高于左舷侧压力幅值.

(3) 当船艉结构某阶耦合模态固有频率靠近螺旋桨激励力频率时，振动幅值会明显增大，而当结构的某阶耦合模态固有频率远离螺旋桨激励力频率时，振动幅值则明显降低.增加板厚或者安装加强筋可以改变结构特性，从而避开共振频率，达到减振的目的.需要注意，增加板厚或者安装加强筋后，如果使得结构某阶耦合模态固有频率更加接近激励频率，结构振动反而会明显增大.