冰与斜面结构作用过程的离散元模拟与分析

根据冰块破碎形式的不同，可以将冰区海洋工程结构分为直立结构和斜面结构两种形式.其中，冰与直立结构作用主要发生挤压破坏，而冰与斜面结构作用主要发生弯曲破坏.相同条件下海冰发生弯曲破坏产生的冰荷载峰值要远小于海冰发生挤压破坏时产生的冰荷载峰值.例如，Timco等对波弗特海域沉箱结构的冰荷载进行了现场实测，通过对实测数据的分析发现，海冰发生挤压破坏时产生的冰荷载约为弯曲破坏时产生冰荷载的6倍.海冰发生弯曲破坏的概率又与斜面结构的倾角有关，如白旭等基于模型实验和现场实测数据，对船体斜面与海冰作用的过程进行研究，总结出破坏模式与倾角的关系：当斜面倾角小于70° 时，海冰以弯曲破坏为主；当斜面倾角在70°～82° 之间时，挤压破坏和弯曲破坏同时存在；当斜面倾角大于82° 时，海冰主要发生挤压破坏.因此，斜面结构倾角是冰区海洋工程结构设计时需要考虑的重要因素之一.

针对海冰问题，数值模拟方法是重要研究手段之一，其中离散单元法(DEM)广泛用于海冰问题的模拟.如Hopkins等采用圆盘单元模拟了浮冰在海浪作用下与海洋结构相互作用过程，通过将模拟结果与试验数据比较，验证了模型的合理性.李紫麟等基于圆盘单元模拟了船舶在碎冰区航行所受冰荷载的问题.上述研究都是基于DEM模拟破碎的浮冰与海洋工程结构的作用.为了同时模拟海冰与结构作用破碎的物理过程，有学者在离散单元法的基础上引入虚拟的“黏结带”概念，构造出具有黏结-破碎功能的离散单元模型，如球体离散单元.但是这些工作都是基于均匀的离散单元，通过规则排布离散单元来构建海冰，这种模型冰破碎形式固定，不能很好地模拟海冰由于气泡、杂质及冻结不均匀等因素造成的海冰物理力学的随机性、非线性及各向异性的特性.因此，有必要构建一种更能体现海冰这种物理力学特性的海冰模型.

综上，本文通过非统一尺寸且初始分布随机的圆盘单元进行黏结来构建平整冰模型.这种平整冰模型相较于规则分布的离散单元模型冰，更能反映海冰破碎时的随机性、非线性及各向异性等特性.本文采用这种非规则排布的离散元海冰模型模拟平整冰与斜面结构作用并发生破碎的动力过程，分析斜面倾角对冰荷载的影响以及海冰破坏模式与斜面倾角间的关系.所构建的数值模型及相关研究内容可以为海冰的离散元数值模拟研究以及斜面海洋工程结构的抗冰设计提供参考.

1 离散元模型

1.1 扩展圆盘单元

参考自然界莲叶冰的形态，Hopkins构造了扩展圆盘单元模型，并用这种圆盘单元模拟了浮冰在海浪作用下与海洋结构相互作用过程，通过将模拟结果与试验数据比较，验证了模型的合理性.这种扩展圆盘单元是通过对一个平面圆盘和球体做闵可夫斯基和运算得到的，可以简单地描述为在二维圆盘表面上的每个点都扩充一个球体，这样就得到了一个表面光滑并具有一定厚度的三维圆盘模型.这种扩展圆盘单元的直径等于平面圆盘直径和球体直径之和，单元的厚度是球体的直径.根据圆盘的几何性质可以把圆盘单元间的接触情况分为平面-曲面、曲面-曲面和平面-平面接触这3种类型.根据接触单元间的相对位置判断其接触类型，进而计算得出单元间的变形量，再根据弹簧-黏壶模型计算出单元间的接触力.圆盘单元受到的外力除了单元间的接触力以外，还有浮力、拖曳力及附加质量等.

所有数据应用SPSS 17.0进行统计学分析，计数资料以频数及百分率表示，组间比较采用χ2检验，计量资料以均数±标准差表示，组间比较采用t检验，以P<0.05为差异有统计学意义。

1.2 非规则分布的圆盘单元及其黏结-破碎模型

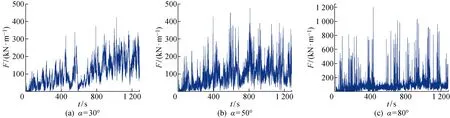
根据现场实测数据的工况，本文对0.5、0.875 及1.25 m共3个冰厚分别进行3次模拟试验，并增加0.6、0.7、0.8、0.9、1.0及1.1 m共6种冰厚工况，并将这几个工况的冰荷载最大值与实测数据进行比较.图5所示为当冰厚为1.25 m时3次模拟的冰力时程.图5(a)～5(c)是冰力时程图，图中为模拟时间，为冰荷载,为峰值冰荷载.冰力时程曲线有分明的波峰和波谷，可以看出作用过程中冰力的加、卸载过程.对比可以发现峰值冰荷载的大小以及出现的时间阶段在一定范围内具有随机性，但是3次试验结果得到的冰荷载峰值的最大值差异不大.

(sin+cos)×

平整冰与斜面结构作用后，海冰发生破碎后会在斜面结构前发生堆积，图9所示为数值模拟的堆积情况截图.当斜面倾角较小时，冰块更容易沿斜面上爬，上爬高度与斜面角度呈反比.因此当斜面角度较小时，形成稳定堆积高度的时间长.而当斜面倾角较大时，冰块不易沿斜面上爬，其爬坡高度有限，因此海冰在斜面结构前的堆积很快达到平衡.当斜面倾角较小时，斜面结构前碎冰的堆积爬坡现象明显，因此由爬坡堆积的冰块重力所造成的荷载对结构的影响也较大.海冰对斜面结构的作用力可以分为两部分，一是海冰爬坡堆积所产生的重力，二是海冰与斜面结构作用发生断裂破碎而产生的动冰力.

(1)

(2)

(3)

(4)

(5)

真实海冰的破坏形式是复杂多样的，本文将海冰的破坏模式简单地分为3种，即挤压破坏、弯曲破坏及剪切破坏.根据正应力的正负可以判别力是拉应力还是压应力，将应力值分别与拉应力极限或者压应力极限对比判断黏结带是发生弯曲破坏还是挤压破坏，将计算得到的剪应力值与切应力极限对比判断黏结带是否发生了剪切破坏.

大型国企，鲁西好肥，肩负起这片福地作物生长的重任，石榴成长的道路上有鲁西化肥一路陪伴，既是对石榴全面营养的补充，又换来老百姓对国企鲁西化肥品质的信赖。

1.3 冰与斜面结构作用的离散元模型

计算域的宽度为30 m，宽度方向上采用循环边界来模拟大范围的斜面结构.平整冰的长度为 86 m，计算域长度200 m，水深15 m，斜面结构的倾角为，如图3所示圆盘单元的运动采用局部坐标系与整体坐标系，局部坐标系固定在每个圆盘单元的质心；整体坐标系固定于计算域内局部坐标系和整体坐标系间的转换通过四元数方法实现为避免计算结果的偶然性，本文对冰排前沿部分海冰单元赋予垂直方向的初始微扰动每个算例进行3次数值模拟，对应3种不同的微扰动初始速度=(-1)×10m/s，其中=1，2，3，表示第次数值模拟时施加在冰排前沿的初始速度微扰动.海冰的断裂强度参考了文献[13-14]的数值模拟工作，其余参数参考文献[1]在原型监测中的工况，相关参数值如表1所示.平整冰在海流的驱动下撞向斜面结构并发生破碎，随着模拟的进行，破碎的冰单元越来越多地在斜面结构前产生堆积.数值模拟中冰排与结构作用过程截图如图4所示.

称取0.013 g甲基橙，加入1 000 mL去离子水中配置甲基橙溶液；用紫外可见分光光度计在460 nm测定加入硅酸镁、硅酸钙、硅胶、硅胶复合材料吸附剂前后吸光度。

1.4 模型验证

海冰是由纯冰、卤水及空气组成的复杂物质，具有非匀质的特点.数值模拟中为了更贴近海冰的非匀质特点，采用初始分布为非规则、非统一尺寸的圆盘单元进行黏结来构造平整冰，如图1所示.采用这种非统一尺寸扩展圆盘单元构建的平整冰可以真实模拟海冰非匀质的力学性质，使海冰破碎更加随机，更符合真实的海冰破碎过程.平整冰与斜面结构作用时，海冰破碎长度与冰厚之比约为7，而本文算例中最薄的平整冰厚度是0.5 m，即海冰的破碎尺寸约为3.5 m.平整冰的破碎是黏结带的破碎，圆盘单元不破坏，因此圆盘单元的尺寸要小于破碎尺寸，这样圆盘单元尺寸对破碎尺寸的影响较小.本文数值模型中选择的圆盘直径范围为1.59～2.65 m.平整冰模型构建时，首先计算每对相邻圆盘单元间的最短距离，当单元间的距离小于冰厚的一半时进行黏结，否则不黏结.依据这样的判断准则，圆盘单元将与其直接相邻并距离较近的单元黏结.如图1中的1号单元，与其相邻的2～8号单元直接相邻且距离均小于0.5(为冰厚)，因此将它们黏结在一起.基于这样的算法遍历所有圆盘单元，最终将计算域中的所有满足条件的圆盘单元黏结在一起，形成具有一定孔隙的平整冰模型.

将数值模拟中得到的冰荷载值除以斜面结构的宽度，得到单位宽度的结构所受冰荷载情况，如图6所示.其中，黑色实线由实测数据中海冰发生挤压破坏的数据进行线性拟合得到；黑色虚线由实测数据中海冰发生弯曲破坏时的数据进行线性拟合得到；红色实线由实测数据中海冰发生混合破坏模式时的数据进行线性拟合得到.比较发现，数值模拟的冰力峰值基本在混合破坏拟合直线偏下的区域中.数值模拟的结果均比挤压破坏的冰力小、比弯曲破坏的冰力大，并在混合破坏冰力范围内.

2 斜面倾角影响分析

2.1 斜面倾角对冰荷载的影响

基于该模型，本文模拟了海冰与不同倾角的斜面结构作用的动力过程.海冰与斜面结构作用的受力分析如图7所示.根据M-C理论有=，为碎冰上爬时与斜面结构产生的摩擦力，为斜面对碎冰的支反力将力分解到水平方向和竖直方向可知，当竖直方向分量为0时可以认为海冰仅发生挤压破坏，即sin-cos=0极区海冰与海洋工程结构间的摩擦因数范围是0.04～0.14，当等式成立时倾角的范围是 82° ～88° .本文数值模拟中采用的海冰与结构间的摩擦因数是0.1，故当等式成立时对应的倾角为84.3°.由于仅发生挤压破坏时冰荷载增长迅速，所以为保守起见，本文取斜面最大倾角为 82° .

综上，设定斜面倾角工况分别为30°、40°、50°、60°、70°、75°、80° 和 82° .设定冰速为0.05 m/s，冰厚为1.25 m，冰排长度为86 m，模拟时长为 1 285 s，部分冰荷载时程如图8所示.比较发现，冰荷载大小(整体变化趋势)随着斜面倾角的增加而增加.根据图8中冰荷载整体的变化规律，可将结构所受冰荷载分为两个阶段，即冰力发展阶段和冰力稳定阶段.在冰力发展阶段，冰力均值逐步增加；在冰力稳定阶段，冰力均值变化较小.当斜面倾角较小时，冰荷载有较长的发展阶段，如图8(a)所示；而当斜面倾角较大时，冰荷载很快进入稳定阶段，如图8(c)所示.当斜面倾角较小时，海冰会在斜面上爬升并发生堆积，因此冰力发展阶段主要是由海冰在斜面上爬坡堆积的重力作用造成的，当堆积稳定后，冰力就进入稳定阶段.而当斜面倾角较大时，海冰不容易发生爬坡堆积，故冰力会较快进入稳定阶段.

治安法官作为英国的历史遗产，一直没有中断，幸存久远，运行良好，并发展嬗变为现代英国治安法官。因为治安法官在英国历史上每个关键时期显示了治安法官群体特有的气质和品质，审时度势，勇于自我革新，顺应统治者和形势的需要，就连资产阶级革命也没有将其摧毁打碎，反而为资产阶级所利用，治安法官最终幸存下来。因此，现代英国治安法官积淀了深厚的历史文化底蕴，带有极易察觉的历史痕迹，再现了英格兰法律发展历史连贯性。

冰荷载理论研究中，根据二维理论模型，在作用初期，即没有大量碎冰堆积形成时，其冰力的计算公式为

寝室文化设计犹如一个家庭的装修风格，舒适的环境往往使人身心愉悦，心理的归属感和安全感会明显上升。相反则会使寝室成员缺乏安全感和归属感，不仅不利于寝室人文文化的建设，也不利于大学生身心健康的发展。因此工作室的成立具有极大可行性和提升大学生人文素养的现实意义。同时，通过加强大学生寝室文化建设，发挥其育人的功能，为学生构建一个和谐、积极向上的寝室环境，以健全的人格，为社会主义现代化建设不断努力。寝室文化工作室指导工作涉及内容广泛，要提升学生的创造性思维，设计出更多主题鲜明、内涵丰富的作品，在实践指导工作中还需要不断地学习、思考和总结。

日子就这样一天一天过去，没有什么进展，蒋海峰心里乱糟糟的。约她俩散步，紫云借故不参加，水仙芝也不去。课余时间，蒋海峰窜到水仙芝的座位上，看见一本相册，随手翻了几页，发现了一张发黄的毕业照，他家也有，他的父亲就在合影里。

(6)

(7)

式中：为水平冰力；为平整冰与结构的接触长度；为海冰沿斜面上爬的最大高度.

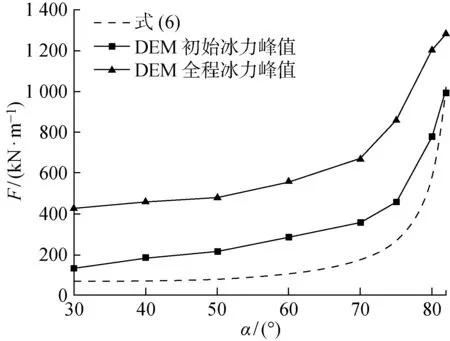
为了验证数值模拟结果的合理性，将本文数值模拟结果与上述理论值计算值进行比较，如图10所示.考虑到理论公式的实用范围是在海冰作用初期，图中增加了数值模拟初期时的冰力峰值采点.对比发现，离散元模型计算得到的初期冰荷载变化趋势与由理论公式得到的变化趋势基本一致，特别是当斜面倾角为82° 时，数值模拟结果与理论值几乎重合.数值模拟结果中，全程冰力峰值较大的原因是数值模拟计算的冰荷载包含了碎冰堆积与爬坡时的重力分力，而理论计算没有考虑碎冰堆积的重力影响，故数值模拟计算的结果比理论公式的计算值大.如图10所示，当斜面倾角小于70° 时，海冰的破坏模式以弯曲破坏为主；当斜面倾角不小于70° 时，海冰的挤压破坏比率超过弯曲破坏的比率.

第四，纠纷解决结果大相径庭。“狗咬羊”案中，张新富死亡的冤屈得以昭雪，尽管没有获得身体上的惩罚，但“青楞”赔偿给死者家属的3000元钱也许更能解决实际问题；而“羊吃花生”案中，王贵春虽然最终被抢救过来，但从情理上讲，王贵春因“青楞”而自杀，抢救花费不少，“青楞”却始终没有以实际行动来表示歉意。可以预测，如果胡光宝自己咽不下这口气，很可能以暴力的方式解决问题，最终胡光宝反而需要因此承担相应的法律责任；如果胡光宝选择司法救济，法院可能按照简易程序进行司法调解或判决，这样胡光宝不仅无法出气，最后的执行也将是个难题。

2.2 海冰破坏模式分析

在冰与结构作用过程中，海冰的主要破坏模式有挤压破坏、剪切破坏及弯曲破坏.为了进一步探究斜面倾角对海冰破坏模式的影响，并验证前文关于冰荷载变化的分析，本文统计出不同斜面倾角工况下不同破坏模式发生的总次数，并计算得到不同破坏模式所占比率()，如图11所示.可见，当斜面倾角为30° 时，海冰发生弯曲破坏的比率为85%.随着斜面倾角的增加，挤压破坏模式的发生概率逐渐增大，弯曲破坏模式所占比率逐渐下降.当斜面倾角为70° 时，海冰发生挤压破坏的概率超过发生弯曲破坏的概率；而当斜面倾角为80° 时，海冰主要发生挤压破坏.结合图10对比发现，挤压破坏使冰力峰值急剧增加.当斜面倾角小于70° 时，海冰主要发生弯曲破坏且冰力峰值增加相对缓慢，因此冰区斜面结构的倾角设计应尽量小于 70° ，同时需综合考虑建造成本以及冰堆积等因素.

3 结论

为了更好地表现海冰物理力学性能的随机性、非线性及各向异性的特点，本文构建了非规则分布且具有黏结-破碎功能的扩展圆盘单元海冰模型，并基于该模型模拟了海冰与不同斜面倾角结构作用并发生破碎的动力过程，获得以下结论：

(1) 基于本文提出的离散元模型模拟的冰力时程曲线有分明的波峰和波谷，可以看出作用过程中冰力的加卸载过程，且冰荷载的峰值大小及出现的时间具有一定随机性.表明该模型可以准确模拟出冰力的加卸载过程以及海冰力学性能的随机性.

(2) 斜面倾角对海冰破坏模式及冰荷载峰值影响较大，通过计算粗略认为，当斜面倾角超过70° 后，海冰发生挤压破坏的概率将超过弯曲破坏，结构所受冰荷载大小也将急剧增大.因此斜面结构的倾角设计应尽量小于 70° .