水泥净浆弹性模量的纳米压痕表征与多尺度计算

纳米压痕技术作为一种测试材料微观力学性能的先进试验方法，能获得材料纳米尺度(1～100 nm)的弹性模量、硬度、蠕变和断裂韧度等力学参数.其基本原理是利用精密传感器连续测量特定形状的压头在材料表面压入过程中的荷载和深度，并通过接触力学理论，计算出待测材料的微观力学参数.1992年，Oliver等提出了纳米压痕试验的 Oliver-Pharr分析方法，并得到普遍应用.目前，纳米压痕技术已被越来越广泛地用于包括水泥基材料在内的各种材料的微观力学性能测量.

1) 从通航净高尺度看，与桥梁净高相关。根据《运河通航标准》[10]规定，长三角地区二～四航道等级的水上过河建筑物通航净高尺度为7 m，对标大运河全线7 m以上净高桥梁，目前共计342座，占比85.3%(见表7)，相比2006年发布《办法》前增长13个百分点，但仍有50座非标桥梁存在，主要分布在浙江内河四级航道，但按照浙江段三级航道整治工程计划，桥梁改建后净高均为7 m。对于其余河段非标桥梁，或因沉降略微下降高度或可通过其他航道绕行，因此运河全线通航净高以7 m为限。

弗雷泽（Fraser）从语用学角度讨论了模糊限制语对施为性句（Performative Sentences）的影响，探讨的是模糊限制语的实用缓和了说话者的言语行为的责任。这种观点被称为“限制性施为”（Hedged Performative）（Fraser，1975）。

水泥基材料的纳米压痕测试最早可以追溯到Velez等对水泥熟料主要成分的弹性模量和硬度的研究，而后由Constantinides等将其引入到水泥水化产物的微观力学测量.针对水泥基材料的多相特性，Constantinides等进一步提出点阵纳米压痕技术，为识别水泥基材料微观各相的力学性能提供了一种有效的解决办法.在此基础上，多位学者测量了水泥水化产物的弹性模量和硬度.微观测试方法的实现，进一步推动了水泥基材料从微观到宏观的多尺度力学性能的相关研究.2003年，Bernard等和Constantinides等提出水泥基材料多尺度模型，采用连续介质力学中经典的Mori-Tanaka法进行弹性参数的跨尺度计算，区别是前者采用水化动力学模型来描述水泥水化产物的体积分数，后者则采用点阵纳米压痕来获得统计意义上的低密度和高密度水化硅酸钙(LDCSH和HDCSH)的相对体积分数.此后，多数研究也主要采用自洽法和Mori-Tanaka法研究水泥净浆的弹性多尺度性能.近年来，添加掺合料的现代水泥混凝土的多尺度弹性表征开始获得更多关注，多采用传统Mori-Tanaka法和自洽法，仅少部分研究采用广义自洽法进行计算.

值得注意的是，纳米压痕试验无法直接探测到纯孔隙相，一般认为，在点阵纳米压痕试验获得的各相的弹性模量参数中，仅包含了部分孔隙的影响.实际上，微观相参数中包含的孔隙均为相内孔隙，例如LDCSH与HDCSH的弹性模量差异，主要来自层间孔和堆积密度，其孔径范围在几十纳米以内，而超过几十纳米的毛细孔径则未予以考虑.因此，本研究基于由点阵纳米压痕试验测量获得的水泥净浆各相的弹性模量和由压汞试验(MIP)测得的孔隙结构，考虑相间较大孔隙的影响，计算水泥净浆的宏观弹性模量，并与试验测试结果进行对比.为考察不同均匀化方法的适用性，对稀疏法、自洽法、Mori-Tanaka 法、相互作用直推(IDD)法和多层次均匀化法进行计算和比较.结果表明，除多层次均匀化法外，其他方法都可以得到近似结果，并与试验数据吻合良好.

1 材料与方法

1.1 材料配比

使用 P.O 42.5普通硅酸盐水泥制备水灰比(w/c)分别为0.2、0.4和0.6的水泥净浆试样，在温度=(20±2) ℃、相对湿度大于95%的标准养护条件下养护180 d后，进行纳米压痕、MIP和宏观弹性模量试验.其中，纳米压痕试验和MIP采用70.7 mm的立方体试件，弹性模量试验采用尺寸为 70.7 mm×70.7 mm×220 mm的棱柱体试件.由X射线荧光光谱(XRF)分析得到的水泥参数如表1所示.

1.2 试验方法

该方法并没有考虑夹杂之间的相互作用，因此一般只适用于夹杂量很少的情况(≈5%).

通过调查，轿车前挡风玻璃设计倾斜角度一般为30°～45°，货车及部分特种车辆前挡风玻璃设计倾斜角度多为60°～90°，计算结果为车窗玻璃下缘到地面距离H的范围为0.9～1.3 m。另外，通过对北京市二环路沿线公交车车型的调查，公交车车窗底部至地面的垂直距离约为1.05 m，在计算结果范围之内。

对于荷载-位移曲线，也即荷载-压入深度(-)曲线，接触约化模量()和压痕硬度()可由下式得出，即

(1)

(2)

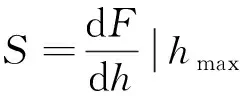
(3)

式中：为压头形状修正因子，对于Berkovich压头，=1.05；为接触刚度；为最大压痕深度；为处的投影接触面积，可以表示为有效接触深度()的多项式函数，即=().

对于各向同性的均质材料，接触约化模量与弹性模量()具有如下关系:

(4)

该方法具有与广义自洽法同阶的精度，同时可以避免广义自洽法求解困难问题，具有较好的应用前景.

然而，从目前的发展来看，多元矛盾纠纷化解机制并未真正走向多元，而是越来越走向“一元”，具体而论，呈现出一种权力主体一元、执行主体多个的发展态势。

(5)

不同的颜色能带来不同的心理效应，如表2。比如红色的警示路牌能刺激道路上其他驾驶员的情绪，给他们带来积极的情绪，使他们提高警惕，颜色通过心理效应发挥了正面的作用，但长时间红色的视觉感官又会让看的人产生烦躁的情绪，应用不当，颜色也会产生负面的作业。同时，心理效应又不单单是带来的情绪上面的效应，也有视觉上的效应。比如颜色的深浅和冷暖会影响到颜色的远近感，通常来说，颜色越深，颜色越暖，给人感觉越近，反之仍成立。于是红橙黄等暖色看起来有逼近感，感觉较近，蓝绿紫等冷色系有后退之感，感觉较远。而在交通道路上，有逼近感的颜色更能触发我们的神经，调动我们的情绪，使我们更快同时更积极的做出相对应的行动。

..压汞试验 水泥净浆试件的孔隙率通过压汞试验测得.将待测试样切成约3 mm的小块，放入异丙醇溶液中24 h，以终止水化，然后将试样放入55 ℃干燥箱中干燥48 h去除水分.采用Micromeritics公司生产的AutoPore IV 9500型压汞仪进行标准压汞试验，试验标准接触角为130°，压力范围为0.7～421 MPa.

稳定流模拟的河道边界条件为1981年最大流量和平均流量，初始条件为河道比降。非稳定流模拟的河道边界条件为1981年至1982年逐月流量，初始条件为河道基流。根据稳定流模拟所得水深和流速情况调整模型几何数据并进行保存。建立非稳定流模型时，运用稳定流模拟中调整过的几何数据再现河道情况。模型所用边界条件和初始条件见表1。

..弹性模量试验 水泥净浆试样的宏观弹性模量试验采用行业标准JGJ/T 70—2009中关于静力受压弹性模量测试的相关规范，所获得的弹性模量为应力是40%轴心抗压强度时的割线模量.

1.3 均匀化计算方法

均匀化方法是用复合材料力学计算多相材料多尺度问题的基础方法，其原理是用一个均匀材料的响应来代替非均匀复合材料的平均响应.同时，材料的结构尺度()、微元尺度()分别代表体积单元、夹杂尺度()，应满足尺度上的级差关系，即≪≪在此基础上，通过建立每一相材料的应力与外加应力或者应变与外加应变的局部化关系(设为张量或)，可以得到有效弹性常数的表达式为

(6)

(7)

通过对单夹杂问题的求解可以获得四阶张量的表达式为

(5) 多层次均匀化法.该方法通过引入修正张量，将夹杂置于修正基体中，并在情况下求解(见图2(e))，获得两相情况下的等效弹性常数.然后再利用多层均匀化思路，将获得的两相的等效相与另外一相进行上述计算，得到新的等效弹性常数.以此类推，最后得到复合材料的等效弹性常数，其递推表达式如下：

=[+(-)]

(8)

式中：为四阶单位张量；为与夹杂形状相关的张量.与Eshelby张量()的关系为

=

(9)

对于水泥净浆多夹杂问题，主要是利用对基体和远场作用应变的合理假设，将多夹杂问题转换为单夹杂问题进行求解.主要讨论下述5种方法的有效性.

(1) 稀疏法.该方法将每个夹杂置于无限大的基体中，并在远场作用初始应变()情况下求解(见图2(a))，得到等效弹性常数的显式结果：

(10)

..纳米压痕试验 在进行纳米压痕测试之前，需将水泥净浆试样切割成直径约为10 mm的小试块，并将其浸泡在异丙醇溶液中48 h，以终止水化.然后将小试块嵌入速凝树脂中完成纳米压痕试样成型，并对镶嵌试样进行打磨和抛光.打磨时用目数分别为400、800、1 200、2 000 目的金相碳化硅砂纸依次打磨，之后用颗粒粒径分别为3、1、0.5、0.25 μm 的酒精基金刚石悬浮液依次抛光.激光显微镜测得试样表面粗糙度约为150 nm.

(2) Mori-Tanaka法.该方法将每个夹杂置于无限大的基体中，并在远场作用基体平均应变()情况下求解(见图2(b))，得到等效弹性常数的显式结果：

(11)

该方法适用于夹杂量较多的情况(≈30%)，较为常用.

(3)自洽法.该方法将每个夹杂置于无限大等效基体中，并在情况下求解(见图2(c))，得到等效弹性常数的隐式结果：

=+

(12)

该方法的求解过程较复杂，但比较适用于求解无明显基体相的复合材料.

(4) IDD法.该方法将每个夹杂置于无限大的基体中，并在远场作用有效应变()情况下求解(见图2(d))，等效弹性常数的显式结果：

(13)

(14)

(15)

(16)

式中：为待测材料的泊松比；和分别为金刚石压头的弹性模量和泊松比在本研究中，设=024点阵纳米压痕的数据处理采用经典解卷积法，假定各相力学性能和服从正态分布，通过最小化理论模型与实测结果的累积分布误差来获得各相的和均值为

系统性是初中体育高效课堂的基本特征之一，主要指的是体育教师在设计课堂教学活动时，需要将系统论作为教学设计的指导思想，使整个课堂成为一个有机的整体。初中体育高效课堂其本身就是一个有效的教学系统，包括教材与学情、指导思想、教学目标与教学方法、教学重难点以及教学评价等等。所以，在打造初中体育高效课堂时，要坚持以系统观点，对课堂教学的各个要素进行全面分析，例如，创设教学情境，激发学生参与积极性，确保教学活动能够有序开展。

近年来，高台县认真贯彻落实国家“一带一路”战略，坚持把促进农产品“走出去”作为转变农业发展方式、调整产业结构、促进农民收入的重要抓手，着力在建基地、壮龙头、创名牌、拓市场、活流通上下工夫，初步形成了外向型农业产业体系和产、供、销一体化发展模式。

[(1-)+]

(17)

(18)

(19)

采用iMicro Nanoindenter纳米压痕试验仪进行纳米压痕试验，其动态接触模块(DCM)头配备尖端半径小于20 nm的金刚石Berkovich压头.在连续刚度测量(CSM)模式下进行测试，荷载和位移分辨率分别为50 nN和小于0.04 nm.试验设置了包含400(20×20)个点的点阵，测点的间距设置为 60 μm，以消除不同点之间的相互影响.标准的纳米压痕测试流程主要包括3个步骤(见图1)：① 采用常应变率(0.05 s)加载至预设深度 2 000 nm；② 在最大荷载处持载10 s，以消除蠕变影响；③ 线性卸载至0.

2 试验结果与分析

2.1 纳米压痕试验结果与分析

在传统的纳米压痕试验研究中，通常将水泥净浆中所测到的点分为含孔相(PP)、LDCSH、HDCSH、氢氧化钙相(CH)和超高性能相(UHP，主要以未水化水泥颗粒为主).其中最主要的水化产物为LDCSH和HDCSH，如图3所示.图4为w/c=0.4的水泥试样在200 nm深度处的弹性模量的解卷积计算结果.表2为不同水灰比试样的点阵纳米压痕试验所获得的各相弹性模量与体积分数.

二是虚假信息的泛滥。网络上充斥着大量虚假新闻、虚假事件以及损害他人利益、损害国家名誉等的不良信息，影响公众对舆论的判断力。一些违法分子甚至在网络上发布凭空捏造一些子虚乌有的事件，煽动公众情绪，尤其是煽动公众损害他人利益的信息、影响政府声誉的信息、甚至是危害国家安全的信息，对社会公共安全形成威胁。

从结果可知，LDCSH的弹性模量约为20 GPa，其体积分数随水灰比的增加而增加；HDCSH的弹性模量约为30 GPa，其体积分数随水灰比的增加而减少.w/c=0.2的净浆试样测得的结果以HDCSH为主；w/c=0.6的试样测得的结果则以LDCSH为主，同时具有比较多的含孔相；w/c=0.4的试样则同时具有相对丰富的LDCSH和HDCSH.同时，由于水化程度相对较低，在w/c=0.2的试样中仍有部分未水化的水泥颗粒，且其弹性模量平均值可以达到 97.18 GPa，而在w/c=0.6的试样中未探测到UHP相.CH相的弹性模量相对不固定，这与其结晶呈各向异性有关，当w/c=0.2，0.4，0.6时，=56，44，38 GPa.含孔相也被称作低硬度相，是受小孔径的孔隙影响的测试点集合，而非具有特定成分的相.该相的弹性模量为10 GPa左右，具有比较大的离散性.

改革需要赋权也需要控权。建立健全司法人员履职保护机制，确保法官、检察官非因法定事由、非经法定程序，不受法律追究；建立健全冤假错案的责任追究机制，要求法官、检察官、人民警察在职责范围内对办案质量终身负责，确保作出的每一项决定都经得起历史检验。

2.2 MIP结果

采用MIP法测得的w/c=0.2，0.4，0.6的净浆试样的孔隙率分别为11.10%、15.51%和29.45%，这3个净浆试样的孔径()分布(5～350 000 nm)如图6所示.水泥净浆中的孔隙大致可以分为凝胶孔、毛细孔和宏观孔3种，毛细孔是水泥净浆水化后期最为主要的孔隙相，在不同水灰比试样的孔隙中均占极大的体积比例.在w/c=0.2的试样中，大部分的毛细孔直径均小于50 nm，大于50 nm的毛细孔较少，且总孔隙率低，这表明水化产物十分致密，孔隙对于材料整体弹性模量的影响可以忽略不计.随着水灰比升高，毛细孔的含量增多，将会对弹性模量产生较显著的影响.

2.3 宏观弹性模量试验结果

3 等效弹性模量计算

3.1 基于点阵纳米压痕测试结果的等效弹性模量计算

基于纳米压痕测量的微观各相弹性模量及其体积分数，分别采用稀疏法、Mori-Tanaka法、自洽法、IDD法和多层次均匀化法，计算3种水灰比水泥净浆的宏观等效弹性模量().为便于计算，假定夹杂均为球形.在等效计算过程中，选用最多的水泥水化产物相LDCSH或HDCSH为基体相，基于各均匀化方法的计算公式，与各夹杂相PP相、CH相和UHP相进行等效计算.其中，w/c=0.4的水泥净浆中，LDCSH作为基体相，HDCSH作为夹杂相.多层次均匀化法的计算策略与其他方法不同，在基体相确定后，每次仅选取一个夹杂相，依次进行等效计算，直至所有相都包含在复合材料中.以 200 nm 深度的结果为例，计算和试验测试所得的对比结果如图7所示.与试验测试结果相比，w/c=0.2的水泥试样多层次均匀化法的计算结果偏高，误差为8.2%.其他方法的计算结果比较接近，误差在5%左右；w/c=0.4的水泥试样多层次均匀化法计算的结果误差大于47%，其他方法的误差约为17%；w/c=0.6的水泥试样，5种方法的误差都在70%以上.可知，直接运用点阵纳米压痕结果进行等效计算，对于水灰比较高的试样存在较大偏差，这是由于高水灰比的试样通常毛细孔隙率较高，而纳米压痕试验结果中仅包含了部分孔径较小的毛细孔隙对宏观弹模的影响.

3.2 考虑孔隙率修正的等效弹性模量计算

为了量化高水灰比试样中较大孔径的孔隙影响，需要确定点阵纳米压痕试验结果中无法直接包含其影响的孔径分布区间范围.根据CSH的孔隙特征，一般认为孔径为0.5～10 nm的孔为CSH凝胶孔，而纳米压痕测量的CSH相为凝胶簇，其堆积孔孔径可达20 nm左右.因此，在本文计算中，不大于20 nm的孔作为相内孔，而大于20 nm的孔作为相间孔.另外，根据纳米压痕测试中的尺度关系，小于0.1的微观相，其影响已计入测量的弹性模量参数之中.基于MIP实验，可以获得孔径在任意范围内的孔隙率及分布.对于200 nm深度的压痕数据，统计孔径大于20 nm的毛细孔体积分数，并将其作为孔隙相，重新计算水泥净浆的等效弹性模量.此处的孔隙相，为包含在水泥基复合材料中，与各个矿相并列存在的相间孔隙.而含孔相则是指在相内包含了较多孔隙或堆积密度比较疏松的复合矿相，由于相内孔隙率高，所以纳米压痕测得的弹性模量较低且离散度高.在计算中，孔隙相考虑为具有一定封闭性的孔隙，体积模量设为不排水情况下水的常温(25 ℃)体积模量2.2 GPa.考虑孔隙相影响的值计算结果如图8所示.除多层次均匀化法外，进行孔隙修正后的各个方法计算得到的w/c=0.4，0.6的水泥试样值与实测弹性模量均比较接近，其计算与实测弹性模量的平均误差分别在7.5%和8%之内.多层次均匀化法预测水泥净浆的结果偏高，原因可能是过高地估计了夹杂之间的相互作用.

于是保安离他而去，花匠离他而去，厨子和女佣离他而去。他们在这里工作太久却没有得到什么，他们的离去太过正常。或许他们至死都不知道他们一直在为玩偶服务——他们是卑贱的奴仆，玩偶是高贵的主人，这实在充满讽刺；或许某一天，当他们突然在自己的脚跟或者脚趾间发现几道淡紫色的伤疤，当他们突然在某一个隐蔽的地方发现属于自己的保修卡、信誉卡、使用说明……当那一天真的来临，迎接他们的，首先是恐惧，然后是哀伤。

数据的统计分析均使用SPSS 16.0软件完成，性别、满意度等计数资料采用χ2检验或秩和检验（有序等级资料），年龄、成绩等计量资料采用t检验或秩和检验（非正态），以（均数±标准差）表示，以P＜0.05表示差异有统计学意义。

3.3 不同计算方法的比较

表4为5种均匀化方法计算所得的3个水灰比试样的等效弹性模量.在5种方法中，自洽法、IDD法和Mori-Tanaka法获得的结果较为接近，稀疏法获得的结果偏低，多层次均匀化法获得的结果则偏高.稀疏法并未考虑各种夹杂之间的相互作用，适应于夹杂量较低的情况，因此，对于水泥净浆这一夹杂量相对较多的材料并不适用.自洽法、IDD法和Mori-Tanaka法均表现出较好的适用性，由于IDD法所得结果为显式结果，求解方便，同时又具有2精度，在水泥基材料多尺度弹性计算中具有比较好的应用前景.

4 结论

通过点阵纳米压痕试验与压汞试验，提出了考虑纯孔隙相修正的水泥净浆宏观等效弹性模量计算方法，为利用传统点阵纳米压痕试验结果无法完全考虑孔隙对材料宏观弹性模量影响的问题，提供了一种解决思路.与宏观弹性模量试验结果的对比表明，计算结果与实测弹性模量吻合良好，计算误差在8%之内，其主要结论如下：

(1) 在采用点阵纳米压痕试验测得的微观各相弹性模量进行等效弹性模量计算时，对于水灰比较高的水泥净浆试样，由于其孔隙率较高，而点阵纳米压痕试验仅包含部分小孔径孔隙的影响，所以无法直接获得较为准确的计算结果.但可以通过压汞试验获得水泥净浆的孔隙率和孔径分布，从而利用压痕过程中的尺度关系，以实现对较大孔径的孔隙影响的定量考虑，所得的计算结果与实测弹性模量吻合良好.

(2) 横向对比不同均匀化方法获得的水泥净浆等效弹性模量，可知在均假设夹杂形状为球形的情况下，多层次均匀化法所得结果偏高，稀疏法所得结果偏低，而自洽法、IDD法和Mori-Tanaka法所得结果具有较好的一致性，且与实测结果相近，因此具有较好的适用性.