逆流连续催化重整工艺烧焦过程的数值计算与分析
郑 晨,姜晓花
(中国石化工程建设有限公司,北京 100101)
石脑油连续催化重整(简称连续重整)是在催化剂作用下,将低辛烷值石脑油转化为富含芳烃的重整生成油并副产氢气的工艺过程。重整生成油可用作车用高辛烷值汽油调合组分,也可用于制取苯、甲苯和二甲苯等化工原料;副产氢气可用作炼油厂其他装置的氢源,综合效益良好。
目前,以美国UOP和法国IFP/Axens公司工艺为代表的连续重整工艺,催化剂在反应器间的流动方向与反应物料一致,即为“顺流”连续重整。在顺流连续重整过程中,随着物料和催化剂的流动,催化剂积炭逐渐加重、催化性能逐渐下降,重整效果逐渐降低;为解决这一问题,中国石化工程建设有限公司从催化剂积炭程度与反应难易程度匹配性出发,提出了“逆流”连续重整的概念,经过与中国石化石油化工科学研究院、清华大学十余年的合作研究,开发出具有“完全自主商业运作权”的逆流连续重整技术并已进行工业应用。其工艺流程如图1所示。由图1可知,该技术的主要特点是:催化剂与反应物的流动方向相反,催化剂的活性状态与反应的难易程度相适应[1]。再生后的催化剂首先进入第四反应器(四反),然后依次经过第三反应器(三反)、第二反应器(二反)、第一反应器(一反),最后返回至再生器。截至目前,逆流连续重整工艺已建成投产5套装置,运行中各项指标均达到或超过设计值,达到国际先进水平。
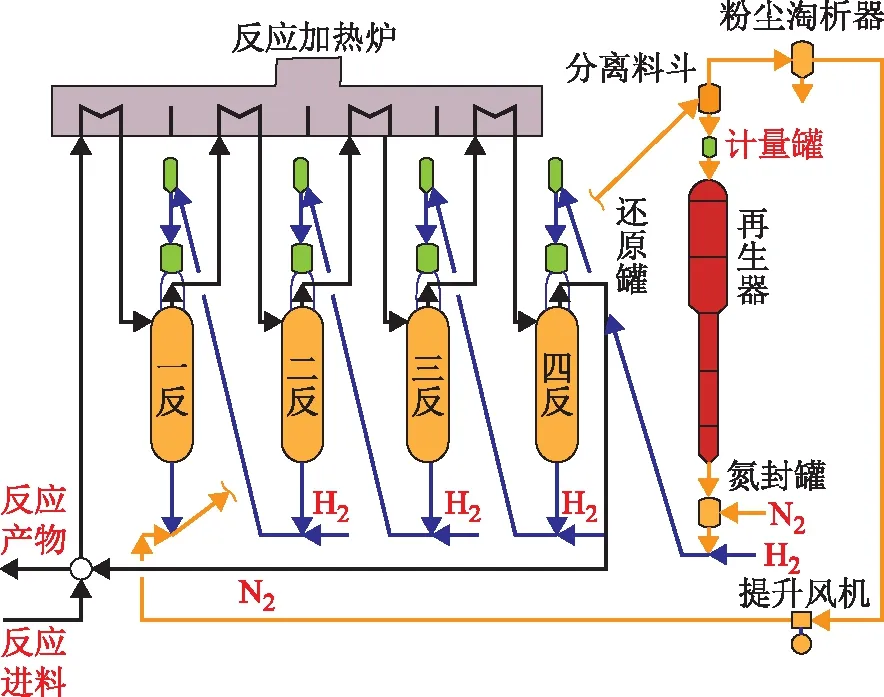
图1 逆流连续重整技术示意
催化剂的连续再生是整个重整工艺中的关键部分,而催化剂烧焦段的传质和性能是再生工艺的关键步骤。逆流和顺流连续重整工艺的主要区别在于:催化剂流动方向不同使反应器中催化剂积炭分布存在差异,并最终影响再生器内的烧焦反应[2]。
潘国庆等[3-4]对Pt-Sn重整催化剂烧焦反应本征动力学进行了试验研究,并建立了描述轴向床层烧焦过程的稳态数学模型,得到了再生气体中氧摩尔分数、催化剂上积炭质量比、床层温度和烧焦反应速率随着床层高度和径向长度的变化关系。熊献金等[5-6]在此基础之上建立了对催化剂烧焦反应数值模拟程序包。阮宇虹等[7]对新一代Pt-Sn重整催化剂烧焦反应本征动力学进行了试验研究,建立了描述轴向床层烧焦过程的数学模型,但该模型存在一些不足:①该模型为稳态条件下的模型,对于动态数据缺乏分析计算能力;②计算得到床层温度最高的位置距离催化剂入口很近(30~60mm),表明催化剂一进入再生器即迅速燃烧,与重整再生装置目前实际运行情况不符;③忽略气固相间传热,认为再生器内每个微元气相和固相的温度相同,也与实际情况不符(如出口催化剂和气相温度不同);④模型参数均是基于传统顺流连续重整装置建立,在用于逆流连续重整烧焦再生过程计算时,均与实际情况有较大偏差。
因此,在前述研究的基础上,结合逆流连续重整烧焦区的动量、热量、质量传递过程及其反应动力学,建立适用于逆流连续重整烧焦过程数学模型,采用数值计算方法进行求解,进而深入研究初始积炭量、催化剂循环速率等操作条件对烧焦区焦炭含量、再生气氧含量、床层温度、气相温度等参数影响,对逆流连续重整再生器的设计和操作条件的优化具有重要意义。
1 模型建立
逆流连续重整装置移动床径向再生器的结构如图2所示。根据该再生器的结构特点,可将其抽象设计为圆环套筒模型。催化剂在重力作用下沿着内、外筛网之间的环状空间自上而下流动,再生气体通过外筛网沿径向进入催化剂床层,穿过床层后通过内筛网进入中心管。采用有限体积法将整个再生器空间划分为若干体积微元。由于再生器对中心线具有轴对称性,因而取环形微元体为基本单元。
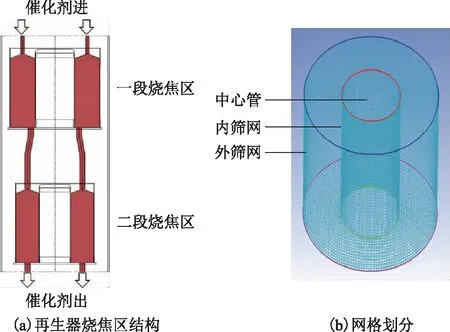
图2 逆流连续重整再生器烧焦区结构及其网格划分示意
结合纳维-斯托克斯方程与传热、反应动力学方程,对每个微元建立数学模型(旋转对称,只考虑轴向(自上而下)和径向方向)。其中,催化剂上的焦炭含量、再生气氧含量、催化剂床层温度、再生气体温度的计算数学模型分别如式(1)~式(4)所示。
(1)
(2)

(3)

(4)
式中:C为焦炭质量比(催化剂上积炭与催化剂的质量比);t为烧焦时间,s;l为从烧焦区底部向上的轴向长度,m;Y为再生气中氧摩尔分数;Vm为再生气摩尔体积,m3/kmol;r为微元体的径向半径,m;Ts为催化剂床层温度,K;Tg为再生气温度,K;h为气-固相间传热系数,kJ/(K·s);ΔH为反应热,kJ/(kg·K);α为表征扩散传热项的系数,m2/s;β1、β2为表征扩散传质项的系数,m2/s;ul为催化剂轴向速度分量,m/s;ur为催化剂径向速度分量,m/s;rC为焦炭消耗速率,s-1;rY为氧气消耗速率,s-1。
为了更好地求解模型,根据实际情况对模型做如下假设:
(1)对于焦炭含量计算模型,假设催化剂轴向移动为平推流,忽略其径向浓度差异;由于焦炭附着于催化剂表面,扩散需要克服吸附能,因此扩散速率极低,忽略其在轴向和径向的扩散。
(2)对于再生气氧含量的计算模型,假设气相在轴向上均匀分布且无返混,在径向上通过各个横截面的摩尔流量相等;由于流速很高,气相在催化剂床层的停留时间为秒级,其对流传质速率远大于扩散传质,忽略其扩散项。
(3)当气相为高速湍流流态时,假设对流导热速率远大于扩散导热速率,忽略温度扩散项;同时假设固相温度影响主要由催化剂轴向流动产生,气相温度影响主要由气体径向流动产生,考虑相间传热。
(4)催化剂的物性(堆密度、孔隙率、比热容等)不受积炭量、温度等因素影响,为定值;
(5)假设催化剂上积炭的碳氢原子比为定值(0.66),其反应表达式[7]如下:

逆流连续重整装置用催化剂的铂含量较低[8],因此可依照高劲松等[9]对低铂含量催化剂烧焦动力学的研究结果计算逆流连续重整过程的反应动力学,表达式如式(5)所示。
(5)
将式(5)代入式(1)~式(4)的数学模型得到如式(6)所示方程组。
(6)
式中:FC为单位面积催化剂的质量流速,kg/(m2·s);φ为催化剂堆密度,kg/m3;η为催化剂有效因子;p为床层压力,MPa;F0为再生气总摩尔流量,kmol/s;ε为空隙率;L为床层轴向高度,m;m′为焦炭与氧气质量比;MO2为氧气摩尔质量,g/mol;w为反应热在固、气两相分配系数;Cp,s为催化剂定压热容,kJ/(kg·K);ρg为气相密度,kg/m3;Cp,g为再生气定压热容,kJ/(kg·K)。
2 模型求解
式(6)所示模型方程组为非线性偏微分方程组,采用数值计算的方法对其进行求解。首先对数学模型在轴向、径向上进行离散化处理:将…分为100等份,由下至上依次记为1,2…i…99,100;将径向…分为40等份,由外网至内网依次记为1,2…j…39,40;分别在两个方向上对一阶导数向后差分,离散为轴向100份、径向40份,共4 000个微元。
床层顶部催化剂入口边界条件为l=L,C=C0,Ts=Ts,0;床层外筛网处再生气进口边界条件为:r=Rout,Y=Y0,Tg=Tg,0;烧焦完全边界条件为dC/dl=0。其中:C0为焦炭与催化剂的初始质量比;Ts,0为催化剂的初始温度,K;Rout为外筛网的半径,m;Y0为再生气的初始氧摩尔分数;Tg,0为再生气的初始温度,K。
对式(6)方程组采用离散化处理,为保证迭代过程收敛精度,采用4级5阶龙格-库塔(Runge-Kutta)显示差分法求解。设定步长为1 s,利用Matlab矩阵运算功能对该数学模型进行矩阵迭代求解,可以大大缩短求解时间,同时利用Matlab图形处理功能输出直观的浓度、温度分布图。
3 参数估计与结果分析
在方程组(6)中,除气固相间传热系数(h)和反应热在气固相间分配系数(w)外,其余参数均可通过直接测量得到。逆流和顺流连续重整工艺的催化剂积炭分布存在差异,影响再生器内的烧焦过程,对于逆流连续重整工艺的烧焦过程需要以实际操作数据对参数h、w作回归估计。
取某逆流连续重整装置的实际操作数据,对再生烧焦区数学模型计算程序中的参数进行校正。将再生器进料数据输入数值计算程序,包括再生气量、再生气温度、再生气氧含量、催化剂速循环率、催化剂温度、催化剂焦炭含量(通过取样分析确定)等,计算得到再生器一、二段烧焦区内任意位置催化剂焦炭含量、再生气氧含量、催化剂床层温度以及再生气温度。对再生器出口计算数值积分后取平均值,得到再生器出口的再生气温度、再生气氧含量、催化剂焦炭含量、催化剂温度。选取同一生产周期内3种不同操作条件为研究对象,其具体参数见表1。其中,条件一为基准条件,条件二在条件一的基础上调整催化剂的循环量,条件三在条件一的基础上调整入口催化剂焦炭含量。
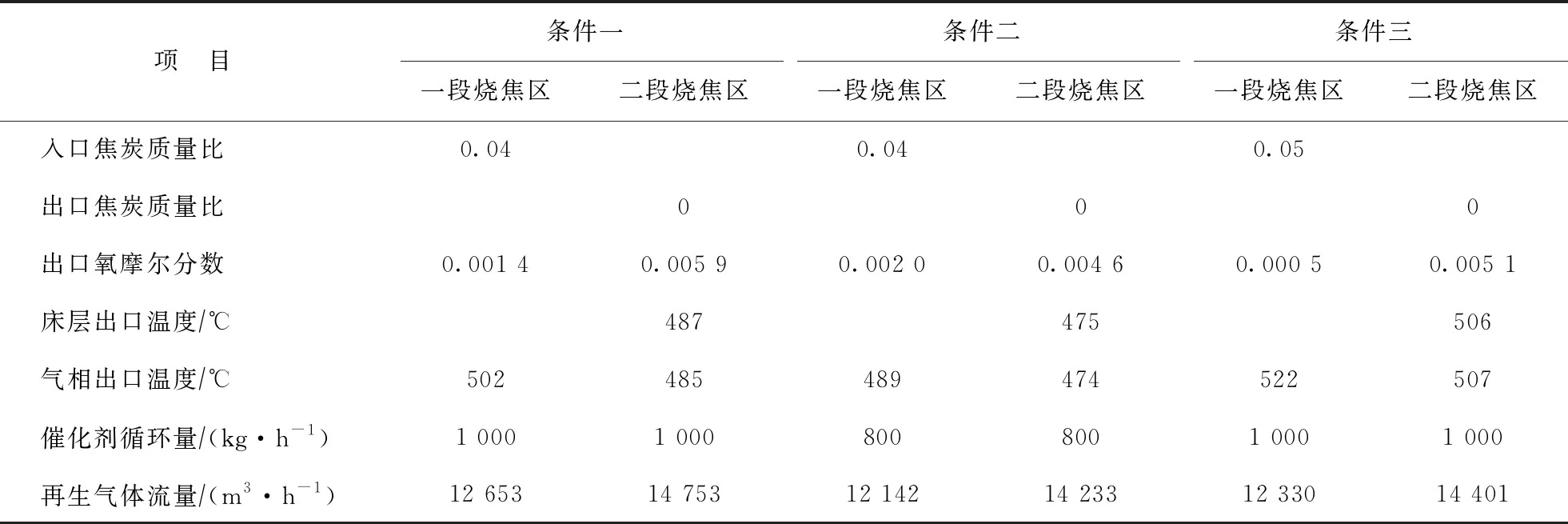
表1 模拟计算的3种操作条件
3.1 条件一工况下的计算结果
在条件一工况下,需要输入的参数主要有进料焦炭质量比(0.04)、床层入口温度(368 ℃)、再生气氧摩尔分数(一段烧焦区0.007 4、二段烧焦区0.006 4)、再生气入口温度(一段烧焦区446.4 ℃、二段烧焦区486 ℃),由模型方程组可计算得到一段烧焦区和二段烧焦区的焦炭质量比、O2浓度、催化剂床层温度、再生气温度的分布,分别如图3和图4所示。图中横坐标轴刻度标示床层径向40等份中由外网至内网依次0~39微元;纵坐标刻度标示为床层轴向100等份中由下至上依次0~99微元。
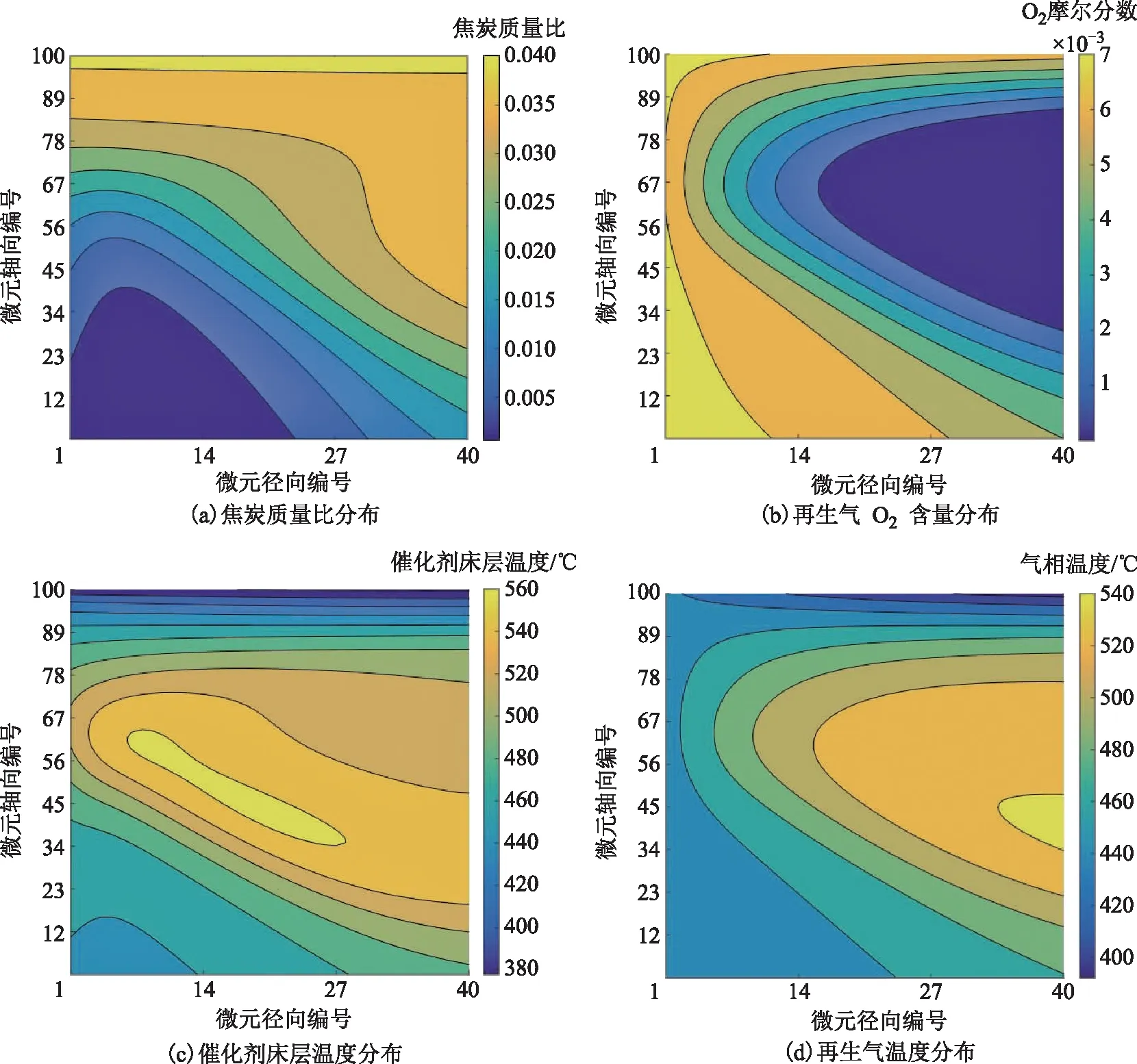
图3 条件一工况下一段烧焦区模拟计算结果

图4 条件一工况下二段烧焦区模拟计算结果
烧焦反应是放热反应,其反应速率主要取决于积炭量、再生气氧含量和反应温度。由图3可知,待生催化剂由顶部进入烧焦区,随着轴向向下距离的增加,催化剂的停留时间逐渐增加,焦炭含量逐渐降低,床层温度逐渐升高。在外筛网附近,催化剂接触到氧浓度高的新鲜再生气,在离开一段烧焦区时积炭基本燃烧完全;而在内筛网附近,催化剂接触到氧浓度低的再生气,烧焦速率下降,在离开一段烧焦区时还有积炭剩余,需转入二段烧焦区进一步烧焦。
再生气自外筛网进入,沿径向自外向内流过催化剂床层;由于烧焦消耗O2,流动过程中再生气中的O2浓度逐渐降低,而再生气温度逐渐升高。在一段烧焦区上部,虽然积炭含量最高,但由于烧焦区入口段的温度较低,导致烧焦速率低,再生气从内筛网处出烧焦区时O2仍有剩余;在一段烧焦区中部,随着温度升高烧焦速率明显提高,再生气流动过程中的O2完全消耗,导致内筛网附近区域的再生气中几乎没有O2,无法发生烧焦反应,因而该区域催化剂上的积炭量几乎不变;在一段烧焦区下部,由于焦炭质量比降低,整体烧焦速率降低,再生气中的O2又有剩余。
温度与烧焦反应的速率密切相关,烧焦反应速率越大温度越高。催化剂自顶部进入烧焦区,随着烧焦反应的进行,床层温度逐渐升高;达到最高值后,由于焦炭质量比降低、烧焦反应速率下降、再生气带走热量等原因,床层温度转而逐渐降低。床层温度最高区域在再生器中下部,通过计算得到床层最高温度约560 ℃。再生气由外向内沿径向流动,不断吸收烧焦反应产生的热量,气相温度逐渐升高,在内筛网处达到最高。
由图4可知,由于大部分积炭在一段烧焦区已经被烧掉,剩余积炭在二段烧焦区轴向较短的流动距离内完全燃烧。因此,二段烧焦区有较大处理裕量,可应对更高的烧焦强度。
条件一工况条件下烧焦区物料和操作参数的计算结果与实际结果比较见表2。由表2可见,通过模型方程模拟计算的操作参数与装置实际操作参数基本一致,说明所建的模型方程组具有良好的模拟精度和准确性。
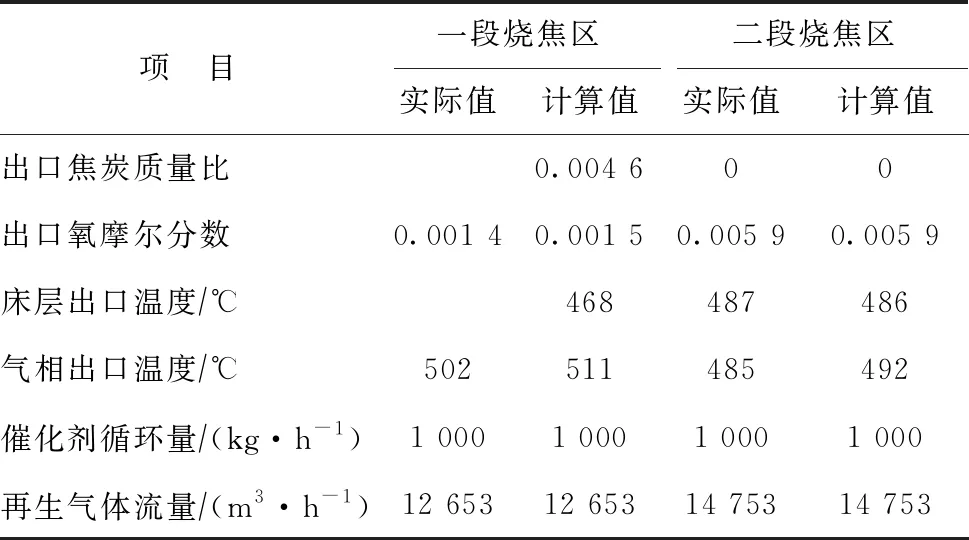
表2 条件一工况下烧焦区操作参数计算值与实际值比较
再生器一、二段烧焦区各设置3组热电偶,分别设置在内筛网处床层最上部、最下部和中间部位。一段烧焦区床层局部温度的实际测量和模型计算结果如表3所示。由表3可知,模型计算与实际测量的床层局部温度有较好的相符性,验证了模型的准确性和可靠性。

表3 条件一工况下一段烧焦区床层局部温度实际值与计算值比较 ℃
3.2 条件二工况下的计算结果
在条件二工况下,需要输入的参数主要有进料焦炭质量比(0.04)、床层入口温度(368.4 ℃)、再生气氧摩尔分数(一段烧焦区0.007 3、二段烧焦区0.004 9)、再生气入口温度(一段烧焦区435.6 ℃、二段烧焦区475.7 ℃),可计算得到一段烧焦区和二段烧焦区的焦炭质量比、O2浓度、催化剂床层温度、再生气温度的分布,分别如图5和图6所示。
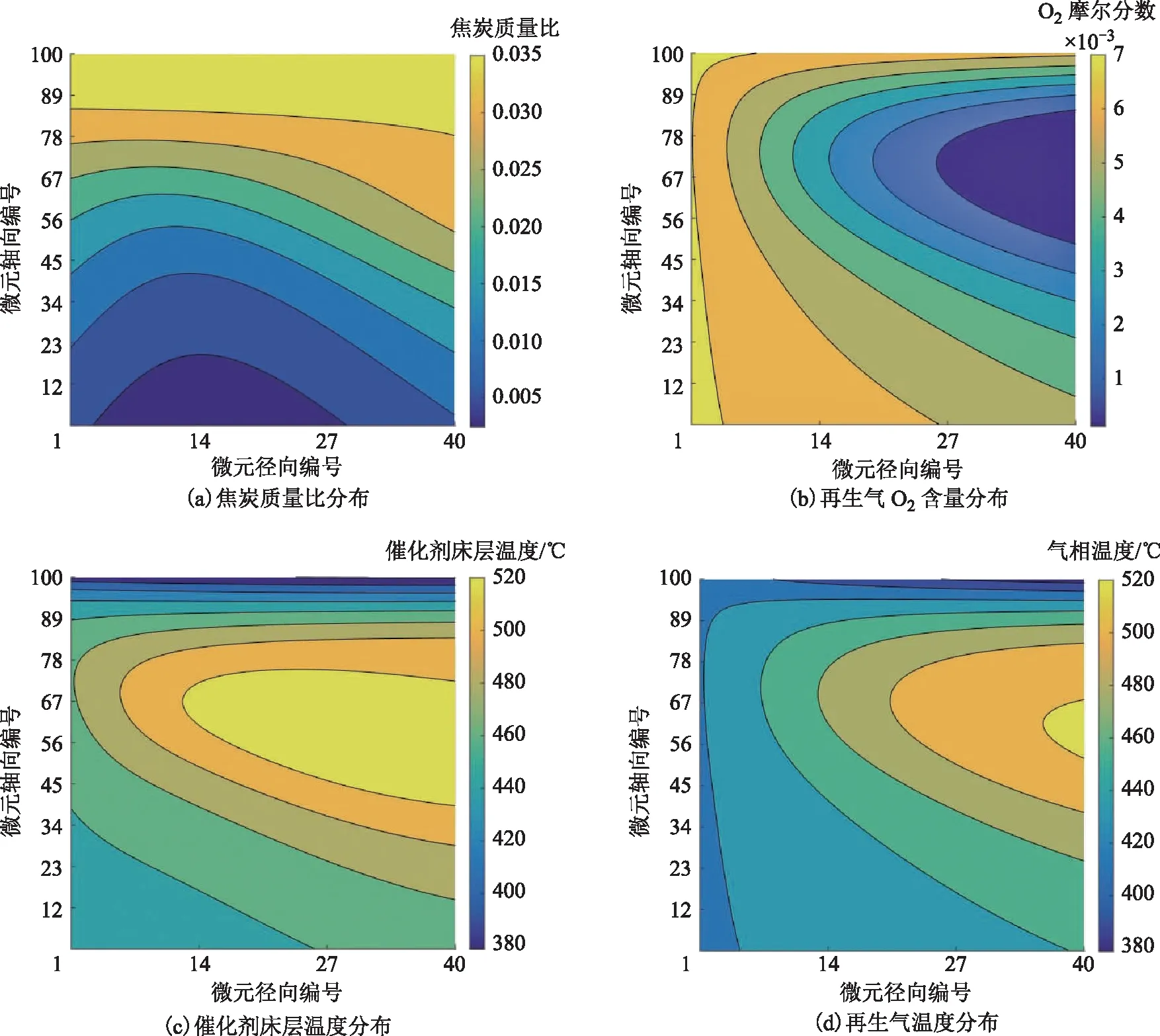
图5 条件二工况下一段烧焦区模拟计算结果

图6 条件二工况下二段烧焦区模拟计算结果
由图5和图6可知,在焦炭质量比相同的情况下,条件二工况下催化剂的循环速率降低,导致整体烧焦强度降低,一段和二段烧焦区的催化剂出口温度、再生气出口温度、床层最高温度均比条件一工况下低10 ℃左右。催化剂轴向流速减小导致烧焦热量更多地在一段烧焦区上部释放累积,因而烧焦区最高温度位置向上部移动。条件二工况下烧焦区物料和操作参数的计算结果与实际结果比较见表4;一段烧焦区床层局部温度的计算值与实际值的比较结果见5。由表4和表5可知,在条件二工况条件下,烧焦区物料、操作参数和局部温度的模型计算值与实际测量值均具有较好的相符性。
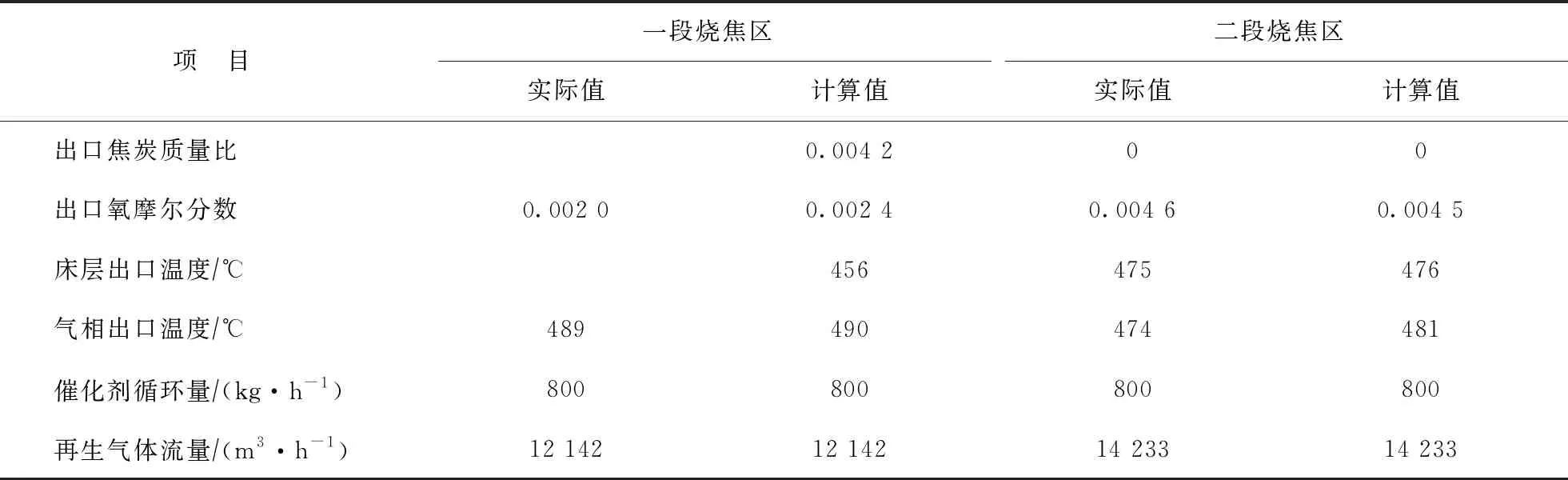
表4 条件二工况下烧焦区操作参数计算值与实际值比较

表5 条件二工况下一段烧焦区床层局部温度实际值与计算值比较 ℃
3.3 条件三工况下的计算结果
在条件三工况下,需要输入的参数主要有进料焦炭质量比(0.05)、床层入口温度(364 ℃)、再生气氧摩尔分数(一段烧焦区0.007 6、二段烧焦区0.005 8)、再生气入口温度(一段烧焦区451.7 ℃、二段烧焦区505.6 ℃),可计算得到一段烧焦区和二段烧焦区的焦炭质量比、O2浓度、催化剂床层温度、再生气温度的分布,分别如图7和图8所示。由图7和图8可知,与条件一相比,条件三在保持相同催化剂循环速率的情况下,初始焦炭质量比提高了25%,导致整体烧焦强度增大,一段和二段烧焦区的催化剂出口温度、再生气出口温度均比条件一工况提高20 ℃左右,而烧焦区床层最高温度接近600 ℃。说明较大的初始焦炭质量比致使初始烧焦反应速率明显提高,再生气流动过程中的O2消耗明显加快,导致内筛网附近存在无O2区域明显增大,O2的不足在一定程度上抑制了内筛网附近区域的烧焦反应,从而导致床层最高温度位置沿径向向外筛网方向迁移。

图7 条件三工况下一段烧焦区模拟计算结果
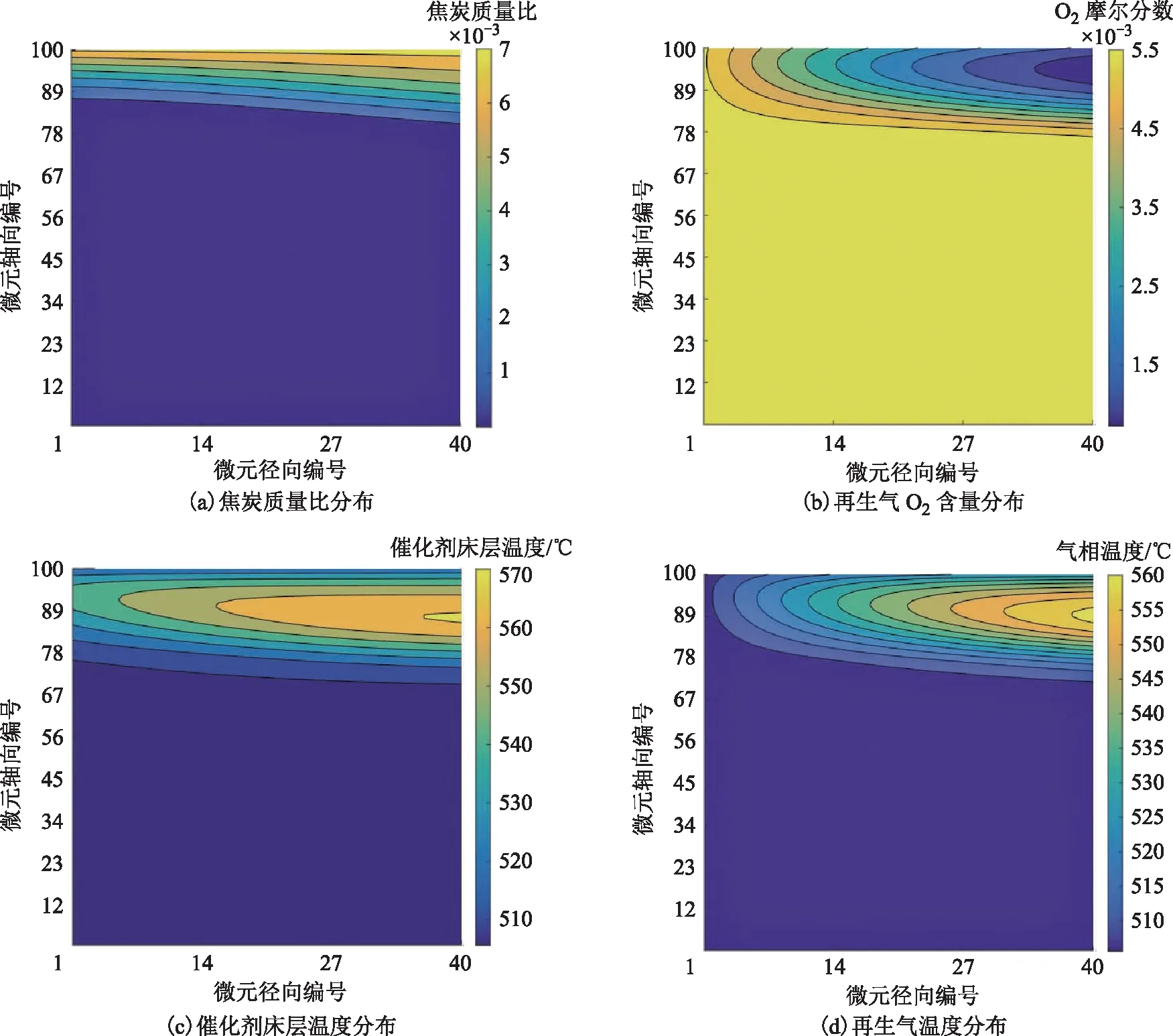
图8 条件三工况下二段烧焦区模拟计算结果
条件三工况下烧焦区物料、操作参数和床层局部温度的计算值与实际值比较分别见表6和表7。由表6和表7可知,在条件三工况条件下,上述参数的模型计算值与实际值的相符性均较好。

表6 条件三工况下烧焦区操作参数计算值与实际值比较

表7 条件三工况下一段烧焦区床层局部温度实际值与计算值比较 ℃
4 结 论
基于动量、热量、质量传递和化学反应基本原理,建立了逆流连续重整再生烧焦区动态数学模型。选取3种操作工况条件,利用该模型对逆流连续重整再生器两段烧焦区内不同位置的焦炭质量比、再生气O2含量、床层温度和气相温度进行模拟计算,发现催化剂积炭量、再生气O2含量和反应温度均影响烧焦反应速率。
在烧焦过程中,一段烧焦区的床层温度由上向下先升高再降低,最高温度出现在一段中下部,与烧焦反应速率一致;再生气中O2含量由外向内逐渐降低,在内筛网中部附近存在无氧区域,影响该区域的烧焦反应;再生气温度由外向内逐渐升高,在内筛网处最高;积炭在一段烧焦区基本燃烧完全,若再生气流量较低,少量剩余积炭需转入二段烧焦区,在二段轴向较短距离内完全燃烧。
对比3种操作工况条件的模型计算结果,发现增加催化剂初始积炭量和(或)催化剂循环量,均可增大烧焦强度,导致催化剂出口温度、床层局部最高温度明显升高。增加初始积炭量,床层最高温度位置向外筛网方向迁移;增加催化剂循环量,则床层最高温度位置显著地向下部迁移。
模型计算结果与装置实际测量结果具有较高的一致性,说明所建模型的计算方法具有良好的准确性,可为工业装置现场操作和工程设计提供可靠指导。

