顾及收发分置影响的海洋大地基准声线跟踪定位方法
辛明真, 葛茂荣, 阳凡林, 刘焱雄, 鲍李峰, 石波, 罗宇
1 山东科技大学测绘与空间信息学院, 青岛 266590 2 德国地学研究中心, 波茨坦 14496 3 自然资源部第一海洋研究所, 青岛 266061 4 中国科学院精密测量科学与技术创新研究院, 武汉 430077 5 自然资源部海洋测绘重点实验室, 青岛 266590
0 引言
海洋大地基准是陆海统筹国家大地测量基准的重要组成部分(刘经南等,2019;杨元喜等,2020),是融合了测绘基准与时空服务属性的国家基础设施,一般采用GNSS与声学定位相结合的技术方法(阳凡林等,2006;刘焱雄等,2006;孙大军等,2019;陈瀚等,2019),通过周期性的测量实现海洋大地基准的长期维持;不仅可以满足日益增长的海洋地球物理科学研究与民用需求,如板块运动监测、大陆架划界、深远海资源开发等(Spiess et al.,1998;Nishimura et al.,2018);又可为GNSS拒止环境下的海洋高精度定位与导航提供一种可替代的技术手段,如执行长航时水下隐蔽任务的潜艇、自主水下潜器等位置精确校准(Tan et al.,2011;Ji et al.,2019;李钊伟等,2019);因其具有极为重要的科学研究价值和军事战略意义,已经成为世界各国争相发展的核心设施与关键技术.
准确获取海洋大地基准的位置信息是发挥其时空基准作用的基础条件,目前主要采用水声测距的方式通过空间距离交会实现海洋大地基准的精密定位(杨元喜等,2017).但受复杂海洋环境动态变化影响,水声距离观测值会受到各类偶然误差、系统误差甚至粗差的综合影响(Zhang et al.,2016;Xin et al.,2018;Chen et al.,2019),因此构建起完善的海洋大地基准定位模型成为了当前的研究重点之一(Xu et al.,2005;Yang et al.,2011).值得注意的是,现有的海洋大地基准定位模型普遍基于收发同置假设,即声波的往返路径和测量载体的位置姿态在较短的观测时延内不会发生变化.一般认为,在浅水的主动声学定位中采用收发同置假设是可以接受的,但对于海洋大地基准的深海定位模式而言,假如在声速为1500 m·s-1的情况下对3000 m水深的基准点进行声学应答式测距,此时声波的往返时延将达到4 s之多,这种情况下仍采用收发同置假设必然会在定位结果中引入一定的模型近似误差.
海洋大地基准收发分置问题的关键在于声波往返路径的准确反演,海水声速的时空变化使得声波的传播路径并非直线,而是发生连续折射的曲线,此即声波的折射效应(Kammerer,2020;辛明真等,2020),因此需要利用实测声速剖面对实际声线进行反演,从而消除折射效应引起的定位误差(Geng and Zielinski,1999;陆秀平等,2012;辛明真,2020).尽管收发分置问题对水声定位导航造成的误差影响已经引起关注(Chen,2014;郭颖,2019),但尚未有研究在射线声学理论框架下,提出水声定位收发分置问题的声线跟踪解决方案.本文针对海洋大地基准定位的收发分置问题,分别提出了基于往返时延差最小的坐标搜索法、基于往返时延分配的方程解算法,实现了收发分置假设下的海洋大地基准的准确声线跟踪定位,可为相关的科学研究和实际解算提供参考.
1 海洋大地基准定位的收发分置问题
海洋大地基准的准确位置通常采用空间距离交会定位的方式确定,如图1所示,测量船可利用搭载的GNSS接收机获得高精度的位置信息,再结合船体姿态和安装参数,通过坐标转换获得声学换能器的坐标,声学换能器向水下基准点发射声信号并接收返回信号,测量声学信号由发射到接收的时间延迟ti,观测历元i=1,2,…,m.
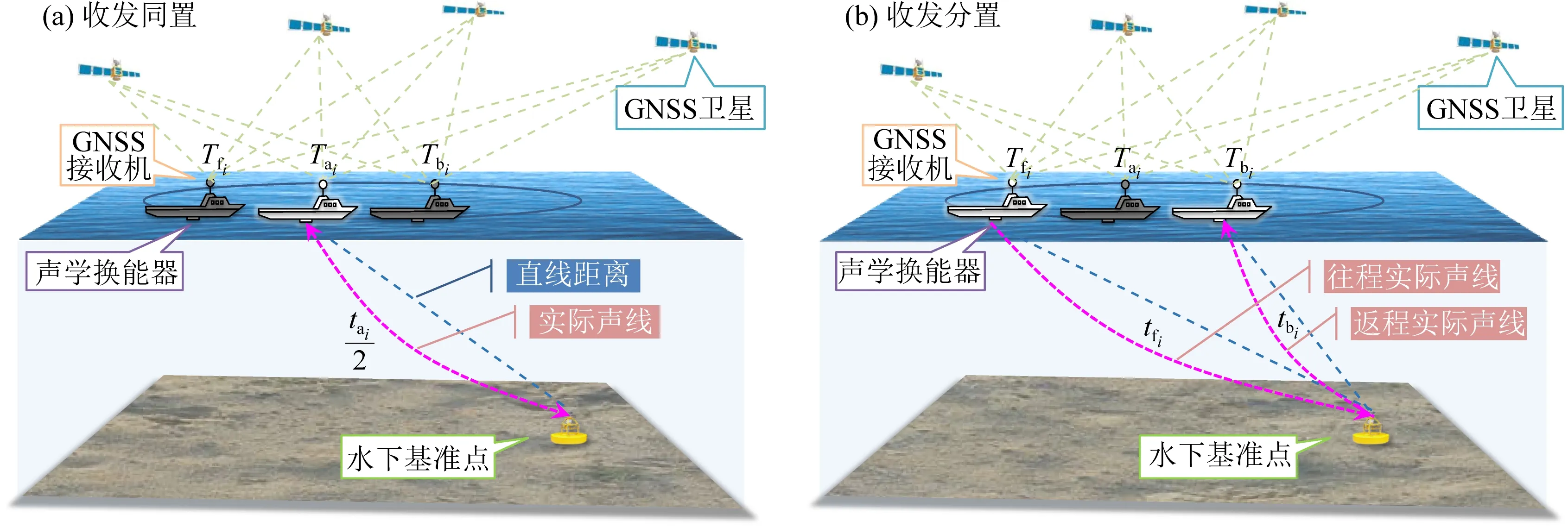
图1 海洋大地基准的水声定位Fig.1 Underwater acoustic positioning of marine geodetic datum
(1)基于收发同置的海洋大地基准定位
收发同置假设在声学信号的发射时刻和接收时刻,声学换能器的位置和姿态没有发生变化,且声波在声学换能器与水下基准点间的往返路径相同(图1a).设声学换能器在信号发射和接收平均时刻Tai的坐标为(xai,yai,zai),声学信号的单程时延为tai=ti/2,则收发同置的距离交会方程为
(1)
式中,(xt,yt,zt)为水下基准点坐标;ρai为收发同置距离观测值,即声学换能器与水下基准点间的直线距离.在声速c为常值的情况下,可以得到声学换能器与基准点的距离ρai=ctai,但海水中的声速存在时空上的变化,因此需要结合实测声速剖面利用声线跟踪对距离观测值进行修正.
(2)基于收发分置的海洋大地基准定位
收发分置认为在声学信号的发射时刻和接收时刻,声学换能器的位置和姿态已经发生了变化,且声波在声学换能器与水下基准点间的往返路径并不相同(图1b).设声学换能器在信号发射时刻Tfi的坐标为(xfi,yfi,zfi),信号接收时刻Tbi的坐标为(xbi,ybi,zbi),声信号的往程(Forward)时延为tfi,返程(Backward)时延为tbi,并有tfi+tbi=ti.则收发分置的距离交会方程为
(2)
式中,ρfi、ρbi分别为往返程的距离观测值.在声速c为常值的情况下,可以得到声学换能器与水下基准点的往程距离ρfi=ctfi、返程距离ρbi=ctbi,且有ρfi+ρbi=cti.同样受海水声速时空变化的影响,需要结合实测声速剖面利用声线跟踪对距离观测值ρfi、ρbi进行修正.
非差距离交会定位的最小二乘解为
X=(ATA)-1ATL,
(3)
由上述可知,海洋大地基准定位的收发分置问题,关键在于对声线往返双程的准确声线跟踪.相较于单程声线跟踪问题,双程声线跟踪问题的难点在于往程、返程声线之间除了时延之和为时延观测值之外,不存在波束入射角等声学信号方面的其他约束条件,下面将结合具体的声线跟踪方法对该问题展开讨论.
2 常梯度声线跟踪方法
目前,基于射线声学理论的常用声线跟踪模型主要有常梯度声线跟踪法、等效声速剖面法等,其中常梯度声线跟踪法不仅应用广泛,而且具有较为严密的理论基础,因此本文将结合常梯度声线跟踪方法对海洋大地基准定位的收发分置问题展开一般性研究讨论.
常梯度声线跟踪是将实际声速剖面分成若干层,假设层内声速以常梯度变化,采用层追加的方法计算声线的传播时间、垂向距和侧向距.如图2所示,若第k层内深度区间为(zk,zk+1),声速区间为(ck,ck+1),波束入射角为θk,k=0, 1, …,n,声线在声速常梯度层中的轨迹为圆弧,圆弧半径Rk为
Rk=1/|pgk|,
(4)

图2 常梯度声线跟踪方法Fig.2 Constant gradient ray tracing method
式中,p为Snell常数,gk为层内声速梯度,可分别表示为
(5)
gk=(ck+1-ck)/(zk+1-zk).
(6)
第k层声线的垂向距、侧向距可以表示成
(7)
改正后的距离为
(8)
声波沿圆弧从sk传播到sk+1所需要的时间tk可表示为
tk=ln(tan(θk+1/2)/tan(θk/2))/gk.
(9)
在声速梯度和观测时延已知的情况下,可以通过迭代计算实现波束入射角和目标位置的准确计算.但对于收发分置问题而言,难点在于观测时延为往程时延和返程时延之和.为此,提出两种不同思路的收发分置声线跟踪定位方法,一种是基于时延误差最小的目标最优坐标搜索法,另一种是基于声线距离分配往返时延的方程解算法.
3 基于时延误差最小的坐标搜索法
海洋大地基准定位的收发分置问题需要分别确定声波的往返声线,这就要求第i个观测历元的往程时延tfi和返程时延tbi是分别已知的,但现有的时延观测值是往程时延和返程时延之和ti=tfi+tbi.收发分置非差距离交会定位应满足最小二乘准则
(10)
其中,时延观测误差Δti=ti-(tfi+tbi),在声速信息已知时,(10)式可以转化为
(11)
以常梯度声线跟踪方法为例,如图3所示,在第i个观测历元下,在信号发射时刻声学换能器坐标(xfi,yfi,zfi)、水下基准点坐标(xt,yt,zt)和声速剖面一定的情况下,若存在则存在声线的唯一直达路径由声学换能器至水下基准点,往程声线在常梯度层内的传播时间为
(12)

图3 顾及收发分置影响的声线路径Fig.3 Sound ray considering the effect of transceiver separation
同理,在信号接收时刻换能器坐标(xbi,ybi,zbi)、水下基准点坐标(xt,yt,zt)和声速剖面一定的情况下,若存在则存在声线的唯一直达路径由水下基准点至声学换能器,返程声线在常梯度层内的传播时间为
(13)
则该观测历元下的往返时延分别为
(14)
4 基于往返时延分配的方程解算法
为提高海洋大地基准定位声线跟踪的计算效率,提出基于声线传播距离对往返时延进行分配的方程解算法,即根据历元内的往程声线距离sfi和返程声线距离sbi,对时延观测值ti进行分配得到往程时延tfi和返程时延tbi
(15)
在往程时延已知的情况下,根据常梯度声线跟踪可以构建得到往程时延与Snell常数pfi间的关系方程
(16)
同理,返程时延与Snell常数pbi间的关系方程
(17)
根据各声速剖面层内的时延之和应该等于总时延观测量,可得
(18)
可以采用非线性方程解析方法对方程(18)进行求解,从而得到Snell常数和声线跟踪所需的波束入射角.这里采用牛顿迭代法来对这个非线性方程进行解算,牛顿迭代法可以表示为
ph+1=ph-F(ph)/F′(ph),
(19)
式中,迭代次数h=0, 1, …,r.对于式(18)的解算,可具体为
F(ph)=∑f(ph)-t,
(20)
F′(ph)=∑f′(ph).
(21)
由此构建起收发分置假设下的声线跟踪与目标坐标的迭代解算过程,结合图4可知该方法的运算逻辑为:(1)在往返时延一定的情况下,确定唯一能够使声线从起始点传播到终止点的波束入射角;(2)确定波束入射角后利用声线跟踪对距离观测值进行修正,再将改正后的距离观测值用于定位解算,从而提高目标的定位精度;(3)较高精度的目标位置可以反算出精度更高的波束入射角,通过反复迭代就可以实现声线跟踪、目标位置的渐次修正.
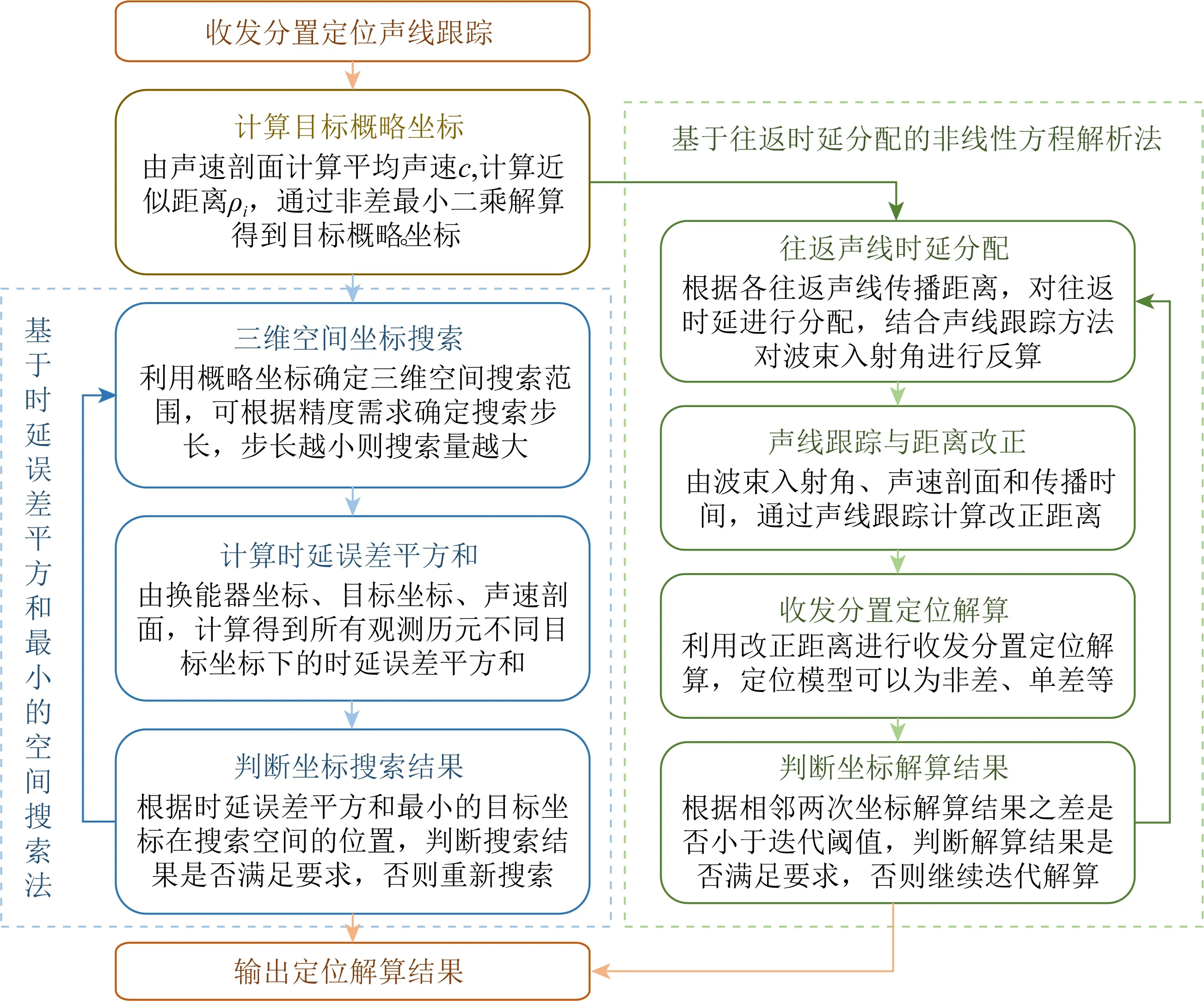
图4 顾及收发分置影响的声线跟踪定位方法Fig.4 Sound ray tracing positioning method considering the effect of transceiver separation
5 海洋大地基准海试
2019年在我国南海海域开展了海洋大地测量基准与海洋导航新技术深海综合试验,在试验区域内以圆形航迹对海底基准点进行了连续观测(图5),水声数据由哈尔滨工程大学的深海高精度水声定位系统采集得到,水声定位测量结束后进行了3次全水深温盐深系统(CTD, Conductivity Temperature Depth)测量,往返测量获得6条声速剖面(图6).首先采用与水声定位测量时间最接近的实测声速剖面svp1down,分别利用收发同置-发射时刻、收发同置-接收时刻、收发同置-平均时刻、收发分置-搜索法、收发分置-解算法进行海洋大地基准定位计算,其中收发同置-发射时刻是指采用声学信号发射时刻的位置和姿态进行解算,收发同置-接收时刻是指采用声学信号接收时刻的位置和姿态进行解算,收发同置-平均时刻是指采用接收和发射平均时刻的位置和姿态进行解算.图7、图8分别为各观测历元内水声信号发射时刻、接收时刻和平均时刻的测船位置和姿态,图9为采用收发同置-发射时刻、收发同置-接收时刻、收发同置-平均时刻、收发分置-解算法得到的距离残差曲线,图10为采用收发分置-搜索法得到的时延残差空间分布,表1中统计了各方法计算得到的目标坐标、中误差及计算时间.为进一步分析声速剖面随时间变化对定位结果的影响,采用不同的声速剖面解算得到的三维坐标变化情况如图11所示.

图5 测船航迹与水下目标Fig.5 Ship tracks and underwater target

图6 声速剖面Fig.6 Sound velocity profiles

图7 信号发射、接收及平均时刻的测船位置Fig.7 Ship position at the time of signal transmission, reception, and average

图8 信号发射、接收及平均时刻的测船姿态Fig.8 Ship attitude at the time of signal transmission, reception, and average

图9 距离残差曲线Fig.9 Distance residuals curves
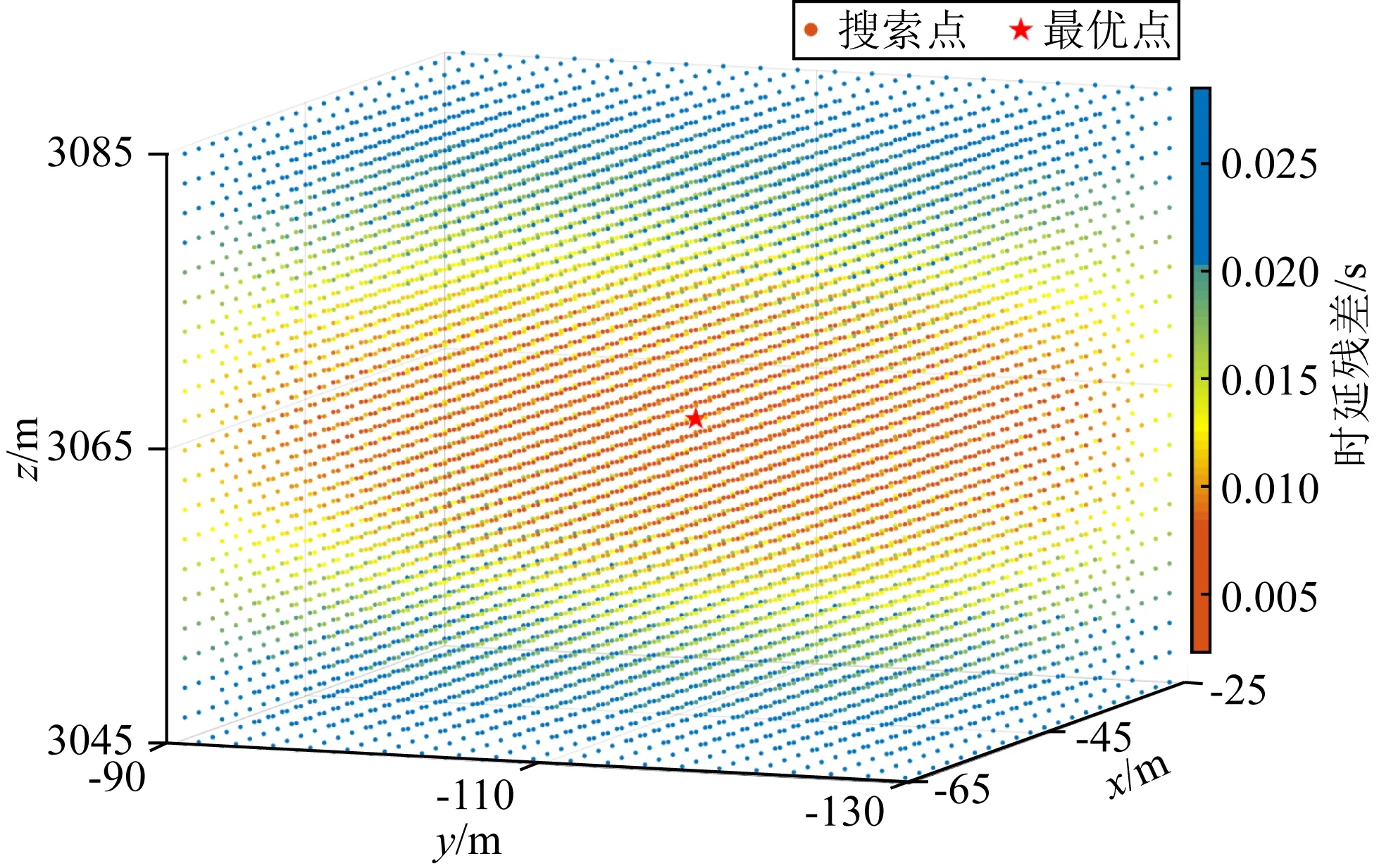
图10 时延残差空间分布Fig.10 Spatial distribution of delay residuals
对实验结果的分析如下:
(1) 结合图7、图8分析可知,在海洋大地测量基准的深度达到3000 m以上的情况下,水声信号的往返时延约为4 s,此时水声信号发射时刻、接收时刻的测船位置和姿态已经发生了明显的变化,收发同置假设下采用平均时刻测船位置和姿态本质上是一种近似平滑处理方法,而且由于忽略了声波往返路径的变化,必然引入一定的模型近似误差.
(2) 由表1统计的解算坐标和单位权中误差分析,收发分置-搜索法和收发分置-解算法的定位结果差异较小,表明收发分置-解算法根据往返声线距离分配时延的方法是可行的;由于收发分置-搜索法是基于时延误差平方和最小,因此其统计结果为时延中误差,并不能与距离中误差进行直接比较;在计算效率方面,收发分置-搜索法的计算时间约为收发分置-解算法的23倍,结合图10可知在三维空间内的坐标搜索会带来较大的运算量,导致收发分置-搜索法的效率较低.
(3) 结合图9对收发同置方法、收发分置方法的距离残差进行对比可知,收发分置-解算法由于能够实现往返声线的有效改正,因此在一个观测历元内存在往程、返程两个距离观测值,而且相比于收发同置方法的距离残差,收发分置-解算法的往程、返程距离残差显著降低;结合表1对收发同置方法、收发分置方法的中误差进行对比,收发分置-解算法的中误差低于收发同置方法的中误差;由此可见收发同置假设的确存在一定的模型近似误差,也验证了顾及收发分置的声线跟踪定位方法的有效性,相比于收发同置-平均时刻的定位精度提高了约20%,相比于收发同置-发射时刻、收发同置-接收时刻的定位精度提高了40%以上.
(4) 进一步分析声速剖面变化对定位解算结果的影响.由图6可知,随着时间推移该海域的声速剖面是在不断变化的,符合海水声速存在时空变化这一普遍认知.结合图11分析声速剖面变化对海洋大地基准定位解算结果的影响,可见水平方向坐标变化明显小于水深方向坐标变化,这是由于具有对称性的圆形航迹使得声速误差在水深方向累积.此外声速剖面变化对定位结果的影响似乎呈现出一定的周期性变化规律,有待通过更多实测数据加以分析研究.

表1 试验结果统计表Table 1 Statistical table of experimental results

图11 采用不同声速剖面的坐标Fig.11 Coordinates using different sound velocity profiles
6 结论
海水作为一种典型的非均匀介质体,其状态参数的时空变化会引起声波的折射效应,如何有效消除折射效应的影响已经成为所有利用声学手段进行各类海洋地球物理测量中存在的一个共性问题.本文面向海洋大地基准的深海准确定位需求,基于射线声学领域广泛采用的常梯度声线跟踪方法,对深海声学定位的收发分置问题进行了一般性的研究和解决,其关键在于声波往返路径的准确反演,即从往返声线路径相同的收发同置声线跟踪问题,转变为往返声线路径不同的收发分置声线跟踪问题,难点在于时延观测值为往程时延和返程时延之和,因此无法对往返程的声线跟踪进行单独处理.为此,结合常梯度声线跟踪提出了基于时延误差最小的坐标搜索法,在满足观测残差平方和最小的原则下将空间距离交会定位问题转变为满足声线跟踪要求的坐标搜索问题,进而提出了基于往返时延分配的方程解算法以提高方法效率,实现了对海洋大地基准高精度定位中收发分置问题的有效解决,同样可以应用于水声测量中同类型的声线跟踪问题.
致谢特别感谢国家重点研发计划“海洋大地测量基准与海洋导航新技术”项目组及深海试验全体科研人员的合作与支持.

