近似常Q模型的黏声各向异性纯qP波逆时偏移

张闪闪， 谷丙洛， 丁奕文， 王霁川， 李振春

中国石油大学(华东)深层油气重点实验室， 青岛 266580

0 引言

地下真实介质中普遍存在着各向异性(Thomsen，1986)，地震波在各向异性介质中传播时，其弹性特征会随着传播方向发生变化，具体表现为地震波速度随传播方向变化而变化(Xu et al.，2020).因此利用各向同性逆时偏移方法对各向异性地震资料进行成像时，由于地震波走时不准确，会导致构造位置成像不准、同相轴能量不聚焦、绕射波收敛不完全等问题的出现.此外，理论和实验证明实际地下介质是黏弹性的(Robertsson et al.，1994).地震波在黏弹性介质中传播时，地下介质固有的黏滞效应会造成地震波能量衰减和相位畸变.在强衰减介质中，受介质黏滞性影响，实际采集的地震资料将存在明显的振幅衰减和相位畸变，采用无吸收衰减补偿的偏移成像方法进行成像时，偏移剖面分辨率将大幅降低——尤其在强吸收介质下方的地层，导致油气预测出现较大误差(Aki and Richards，2002；Shen et al.，2018).

Alkhalifah(1998)提出各向异性声学近似假设并推导了适用于VTI介质的四阶伪声波方程，但该方程包含波场的四阶偏导数，数值求解对内存要求很高.为了降低计算成本，Du等(2008)利用辅助算子将伪声波方程简化为两个耦合的二阶偏微分方程，实现qP波的高效数值模拟.然而，在求解基于声学近似的TTI介质波动方程时，由于将对称轴上的qSV波速度设置为零，导致求解过程存在数值不稳定(Grechka et al.，2004).针对此问题，Fletcher等(2009)假设横波速度大于零，引入与全弹性频散关系一致的二阶项来修正Alkhalifah(1998)所提出的频散关系，并通过坐标变换将VTI介质qP波方程推广到TTI介质.Zhang等(2011)在声学近似条件下，使用伴随算子和协变导数算子将波场变量旋转到局部倾斜坐标系中，直接利用VTI介质中的弹性波方程推导出稳定的TTI波动方程.为了消除震源处的伪横波干扰，Yoon等(2010)提出了椭圆各向异性近似方法，即在震源周围设置“ε=δ”的光滑圆锥形区域，该方法可有效抑制伪横波假象.然而，这种方法虽然旨在减少横波伪影，却改变了地震波的运动学特征，并在纵波模拟中保留了人工横波分量.为了避免这些现象，Zhang(2009)通过滤波投影方法来压制伪横波，以提高成像剖面精度.程玖兵等(2013)推导出适用于任意各向异性介质的qP波伪纯模式波动方程，并利用偏振矢量将纵、横波分离，进一步降低计算成本、压制横波干扰.Xu和Zhou(2014)基于声学近似假设，提出了VTI介质qP波方程，该方程利用伪差分算子将qP波和qS波解耦表示，其数值模拟结果不含伪横波假象.刘文卿等(2016)推导出可用显式有限差分格式求解的TTI介质下qP波控制方程，并提出正则化有限横波方法解决波场传播及数值计算的不稳定问题.黄建平等(2016)推导了TTI介质一阶速度-应力方程并用高阶有限差分格式求解，同时引入了基于PML原理的一阶qP波方程的伪谱法递推格式来实现波场的稳定延拓.Cheng和Kang(2016)等从物理学角度出发，利用波矢量方向与伪横波震动方向的偏差，从耦合的波场中提取出标量纯qP波场，以提高逆时偏移成像精度.郭成峰等(2017)通过对Harlan公式中的非椭圆项进行修正推导出TTI介质纯P波方程，并利用伪谱法和有限差分法联合实现高精度波场延拓及逆时偏移.杨鹏等(2017)推导出解耦的TTI介质纯qP波近似方程，将其中的偏微分算子分解成一个拉普拉斯算子和一个标量算子，其数值模拟结果可有效实现振幅均衡.郭旭等(2019)利用Poynting矢量分离地震方向行波，并在复杂VTI介质中成像，该方法在偏移速度不准确时仍能有效成像.何兵寿等(2021)指出，在TI介质中的qP波逆时偏移领域需要对qP波方程的动力学精度，qP波逆时偏移中的随机边界技术及波场传播方向的求取方法深入研究.

除了各向异性之外，学者们在衰减补偿方面也做出了许多努力.Kjartansson(1979)提出一种不依赖频率的Q值模型，又称为常Q模型.基于常Q模型，Carcione等(2002)推导出包含分数阶时间导数的黏声波动方程来描述声波在衰减介质下的传播，但该方程需要存储所有历史时刻的波场信息，要求极大的存储空间.在此基础上，Chen和Holm(2004)将分数阶时间导数转化为分数阶拉普拉斯算子，通过伪谱法在波数域进行数值求解，提高了计算效率，节约了内存空间.Treeby和Cox(2010)将振幅衰减项和相位频散项解耦表示，方便在成像过程中进行衰减补偿.基于近似常Q模型，Yan和Liu(2013)采用优化的时空域高阶有限差分算法对黏声波动方程进行数值求解，实现了高精度叠前逆时偏移.Zhu等(2014)提出含有分数阶拉普拉斯算子的时域常Q黏声波方程，将振幅衰减项和相位频散项解耦表示，进行稳定补偿的黏声逆时偏移.Li 等(2016)提出利用频散关系将常Q黏声波方程中的振幅衰减和相位畸变进一步分离，使其能够应用于Q值较小地层，有效改善成像效果.吴玉等(2017)基于解耦的分数阶拉普拉斯算子黏声波方程，采用交错网格有限差分法实现数值模拟和逆时偏移，在波场逆时延拓过程中同时完成频散校正和衰减补偿，大幅提高计算效率和成像质量.周彤等(2018)采用多项式多级优化方法校正衰减引起的相位畸变，提高逆时偏移成像精度.在时间域二阶位移形式的常分数阶拉普拉斯算子黏声波方程的基础上，陈汉明等(2020)推导了一阶速度-应力形式的常分数阶拉普拉斯算子黏声波动方程，并提出一种适用于该方程的卷积型完全匹配层吸收边界加载方法.

在黏声各向同性波动方程的基础上，学者们逐渐将其向各向异性介质发展.Suh等(2012)将Zhang等(2010)推导的含有伪差分算子的黏声波动方程扩展到VTI介质，但该方程忽略了衰减引起的相位频散，只对振幅衰减进行补偿.严红勇和刘洋(2012)以Carcione黏弹各向异性理论为基础，推导了适用于黏弹TTI介质的二维三分量一阶速度-应力方程，同时采用旋转交错网格任意偶数阶精度有限差分格式进行求解，实现了该类介质的地震波场数值模拟.Xie等(2015)根据线性黏弹介质的应力-应变关系推导出TTI介质中的黏声波动方程，并发展了TTI介质中的Q补偿成像方法，有效改善剖面质量.Zhu(2017)推导了适用于任意各向异性速度和衰减的时域位移-应力黏弹波动方程，该方程使用分数阶时间导数表征衰减各向异性，因此需要存储所有历史时刻的波场信息，存储量较大.为了降低计算成本，Hu等(2017)发展了基于有限差分解法的TI介质中的Q补偿逆时偏移成像方法，该方法大幅提高了计算效率，便于代码并行化和GPU实现.Bai等(2019)提出VTI介质中振幅衰减和相位频散解耦的Q补偿逆时偏移成像算法，通过改变振幅衰减项前的符号、保持相位频散项不变来进行衰减补偿，大幅提高VTI介质的成像质量.在弱衰减假设条件下，Zhu和Bai(2019)提出了振幅衰减和相位频散解耦的分数阶拉普拉斯黏声VTI波动方程，该方程在保持模拟精度的同时可以大幅提高数值模拟的效率.Hao和Alkhalifah(2019)对正交各向异性介质中标量和矢量黏声波动方程的一般表示形式进行了推导，使其在多个衰减模型下均可灵活适用.Zhou等(2020)将线性黏滞本构关系扩展为一系列整数阶微分项和一个唯一的积分项，实现了振幅和相位的解耦，并提出基于有限差分解法的Q补偿逆时偏移算法框架，该成像方法可在更宽的频率范围内实现精确的衰减补偿.程时俊等(2021)将衰减各向异性和速度各向异性与常Q模型相结合，建立了黏弹性衰减VTI介质模型，并基于分数阶时间导数理论，推导了对应的本构关系和波动方程.

本文基于Xu和Zhou(2014)提出的VTI介质qP波方程，结合常Q模型的松弛函数，推导出新的黏声各向异性纯qP波方程，该方程没有中间记忆变量，可以有效减少计算过程中的内存存储；该方程通过分数阶拉普拉斯算子将振幅衰减项和相位频散项进行解耦，在成像过程中可以有效进行衰减补偿；均匀TTI模型的数值模拟结果表明本文提出的黏声各向异性波动方程无伪横波假象，可以稳定高效地进行数值求解.本文通过两个VTI模型及一个TTI模型进行逆时偏移成像测试，成像结果表明新的方程可以有效提高黏声各向异性偏移成像结果的精度及分辨率.

1 黏声各向异性纯qP波方程

1.1 qP各向异性波动方程

根据Tsvankin(1997)提出的VTI介质中qP波的频散关系：

(1)

其中，V(α)表示相对于对称轴相位角为α的qP波相速度，VP0是qP波沿对称轴的相速度，ε、δ均为Thomsen(1986)各向异性参数，f定义为

(2)

其中，VS0是qSV波沿对称轴的相速度.根据qP波声学近似假设VS0=0，且式(1)中所有参数都是随空间变化的.

在式(1)及Alkhalifah(2000)的研究基础上，解耦的qP波偏微分方程可以表示为

(3)

(4)

式(3)表示qP波在VTI介质中的传播.经过变换，可以得到解耦的VTI介质中的纯qP波动方程(Xu and Zhou，2014)：

(5)

其中，

(6)

考虑到式(5)中qP波是解耦的，我们将黏滞性引入到其中，以期得到纯qP波在TI介质中的黏声波动方程.

1.2 黏声各向异性qP波动方程

在广义各向异性介质中，常Q衰减模型的松弛函数可以表示为

(7)

其中，Γ(·)表示欧拉伽马函数；Gmn表示介质属性的松弛函数；Cmn表示弹性刚度张量；βmn=arctan(1/Qmn)/π，是一个无量纲参数，且对于任意的品质因子均有0<βmn<0.5；t0=1/ω0表示参考时间，ω0表示参考频率.

基于欧拉伽马函数的特性，各向异性黏弹介质的广义连续性方程可以表示为

σmn=Dmnemn,

(8)

(9)

对于TI介质，矩阵Dmn具有与正交介质相同的空元素，但只有5个独立元素：D11，D13，D33，D55，D66.为了更加方便地描述VTI介质中的地震传播特征，我们可以使用Thomsen参数代替矩阵Dmn中的5个独立元素，其关系式可以表示为

(10a)

(10b)

(10c)

(10d)

在这里，假定衰减是各向同性的，则参数βmn可以简化为β.因此，结合(8)—(10)三式，以及柯西方程和运动方程，Kjartansson模型中基于qP波频散关系的黏声VTI波动方程可以表示为

(11)

当β→0(Q→∞)时，上式可以退化为纯qP波各向异性波动方程；当β→0.5(Q→0)时，上式可以退化为各向异性扩散方程.为了避免存储所有历史时刻的波场，我们将分数阶时间导数转化为分数阶伪拉普拉斯算子(Zhu and Harris，2014)，因此，近似常Q模型的黏声VTI波动方程可以表示为

(12)

近似常Q模型的黏声TTI波动方程可以通过旋转VTI介质的坐标系得到，可表示为

(13)

其中，

(14)

(15)

(16)

(17)

(18)

(19)

θ和φ分别是TTI介质对称轴的倾斜角度和倾斜方位角.

基于近似常Q模型的黏声各向异性波动方程包含两项分数阶拉普拉斯算子，可以分别描述各向异性黏滞性介质中地震波的能量衰减及相位频散，并且将振幅衰减及相位频散解耦表示，方程右端第一项描述相位频散，第二项描述振幅衰减.其中，仅振幅衰减的黏声TTI波动方程可表示为

(20)

仅相位频散的黏声TTI波动方程可表示为

(21)

为了说明黏声各向异性纯qP波动方程描述的各向异性衰减介质中地震波的传播特征，此处使用二维均匀TTI模型进行正演模拟.在均匀TTI模型中，横纵向距离均为10 km，网格间距为10 m，设介质速度为3500 m·s-1，密度均匀，各向异性参数ε为0.3，δ为0.25，θ为0.3，品质因子Q为30，炮点位于模型中心，时间采样间隔为0.5 ms，地震记录总长度为1.0 s.采用主频为30 Hz的Ricker子波作为震源函数.

图1为均匀TTI模型在不同方程中的1.0 s波场快照对比图.其中，(1)为TTI纯qP波动方程的模拟结果，(2)为仅振幅衰减的黏声TTI纯qP波动方程的模拟结果，(3)为仅相位频散的黏声TTI纯qP波动方程的模拟结果，(4)为黏声TTI纯qP波动方程的模拟结果.对比图1中均匀衰减模型在不同方程下的波场快照可以发现，与纯qP波各向异性波场快照相比，振幅衰减的黏声TTI波场快照仅呈现出明显的振幅衰减，波场能量减弱；相位频散的黏声TTI波场快照仅呈现出相位的滞后，振幅保持不变；而黏声各向异性的波场快照中同时呈现出振幅衰减及相位畸变，可以表现出地震波在遇到衰减介质之后的传播特征.这说明黏声各向异性波动方程可以描述各向异性衰减介质中地震波的运动学及动力学特征，同时表明方程中的振幅衰减项及相位频散项可以完全解耦，便于在逆时偏移过程中进行衰减补偿.

图1 均匀TTI模型在不同方程中的波场快照(1.0 s)对比Fig.1 Four snapshot partsat 1.0s of the homogeneous TTI model with different wave equations

图2为均匀模型在不同方程下的同一位置的单道地震记录对比.与各向异性纯qP波地震记录相比，黏声各向异性地震记录的振幅明显降低，能量减弱；相位出现明显滞后，表现出相位延迟现象.

图2 均匀TTI模型在不同方程中的同一单道记录(5000 m处)对比Fig.2 Traces from Fig.1 of the attenuating homogeneous TTI model at horizontal 5000 m

图3为基于近似常Q模型黏声TTI波动方程在不同品质因子Q值下的波场快照切片对比，图4为不同Q值下的单道记录对比图.从图中可以看出，随着Q值的减小，波场的振幅衰减及相位畸变程度逐渐增强，这说明文中推导的方程可以描述不同Q值下的地震波传播特征.黏对于TTI介质，倾斜角的引入使得直接采用伪谱法求解分数阶拉普拉斯算子时存在困难，因此在数值求解时需要先使用伪谱法求解空间偏导数，再将结果代入到两个分数阶拉普拉斯算子中求取每个网格点处的值.

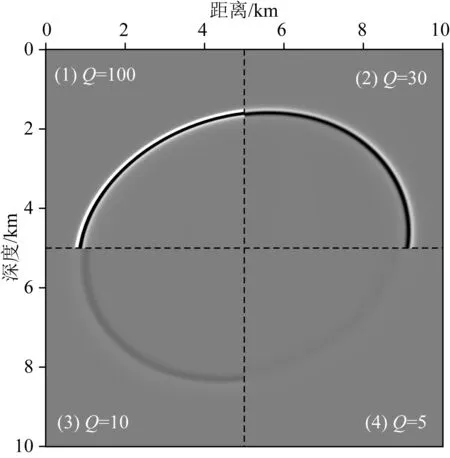
图3 均匀TTI模型在不同Q值下的波场快照(1.0 s)Fig.3 Four snapshot parts at 1.0 s of the homogeneous TTI model with different Q values

1.3 黏声各向异性纯qP波逆时偏移

逆时偏移成像的理论基础是Claerbout(1971)提出的时间一致性原理，其过程可以分为三个部分：震源波场的正向延拓，检波点波场的逆向延拓，以及应用成像条件进行成像.在逆时偏移过程中，波场外推的目的是重建反射点处的入射和反射波场.在黏滞性介质中使用互相关成像条件进行逆时偏移成像时，需要同时对震源波场和检波点波场进行衰减补偿，使波场的能量得到恢复，相位畸变得到校正.在进行波场外推时，Treeby和Cox(2010)及Zhu等(2014)指出，衰减补偿可以通过反转吸收衰减项的符号来实现，但保持等效频散参数不变.因此，需要将振幅衰减项的符号由“+”号变换为“-”号来进行振幅衰减的补偿；同时，由于相位频散项与时间延拓无关(即与频率相关的相位速度在时间上保持不变)，保持相位频散项的符号不变.

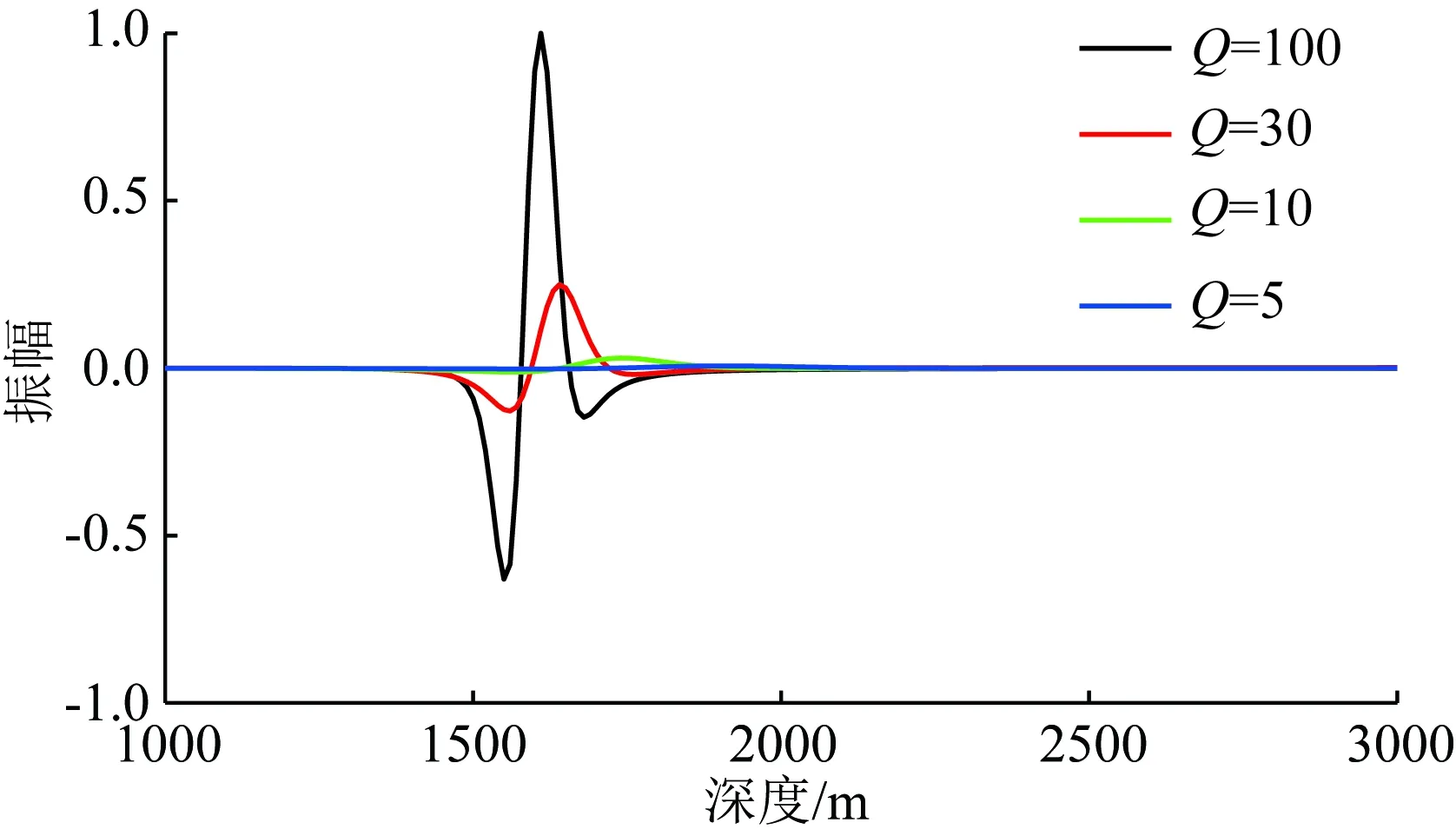
图4 均匀TTI模型在不同Q值下的波场快照(1.0 s)单道对比Fig.4 Single traces from 1.0 s snapshots of homogeneous TTI model with different Q values

利用式(22)即可求解VTI介质中Q补偿的震源波场Us：

(22)

同理，VTI介质中Q补偿的检波点波场Ur可利用式(23)进行求解：

(23)

在偏移成像的实际应用中，地震资料中的较高频率成分比较容易受到噪声的影响.而在黏滞性介质中，由于在波场逆时延拓中进行了衰减补偿，地震波能量呈指数增长，可能会放大不需要的频率成分，增加高频噪声，导致波场延拓的数值不稳定.为了避免补偿过程中高频成分呈指数增长而出现高波数发散问题，本文在计算补偿波场时应用低通滤波方法切除高频噪声，滤波器的截止波数根据介质中最大速度上的截止频率计算得到(Zhu et al.，2014).

2 数值算例

2.1 VTI-Hess模型逆时偏移

首先通过VTI-Hess模型进行黏声各向异性数值模拟，利用数值模拟得到的黏声各向异性地震记录分别进行声波、声波各向异性、黏声波及黏声各向异性逆时偏移成像，对成像结果进行对比，说明它们之间成像效果的差异.图5为VTI-Hess模型，模型大小为9000 m×3750 m，空间间隔Δx=Δz=10 m.共布设了90炮，起始炮点位于(50 m,0 m)，炮间隔为100 m.每一炮均有601个接收点，平均分布在震源两侧，道间距为10 m.地震记录时间长度为6.0 s，时间采样间隔为0.5 ms.采用主频为30 Hz的Ricker子波作为震源函数.

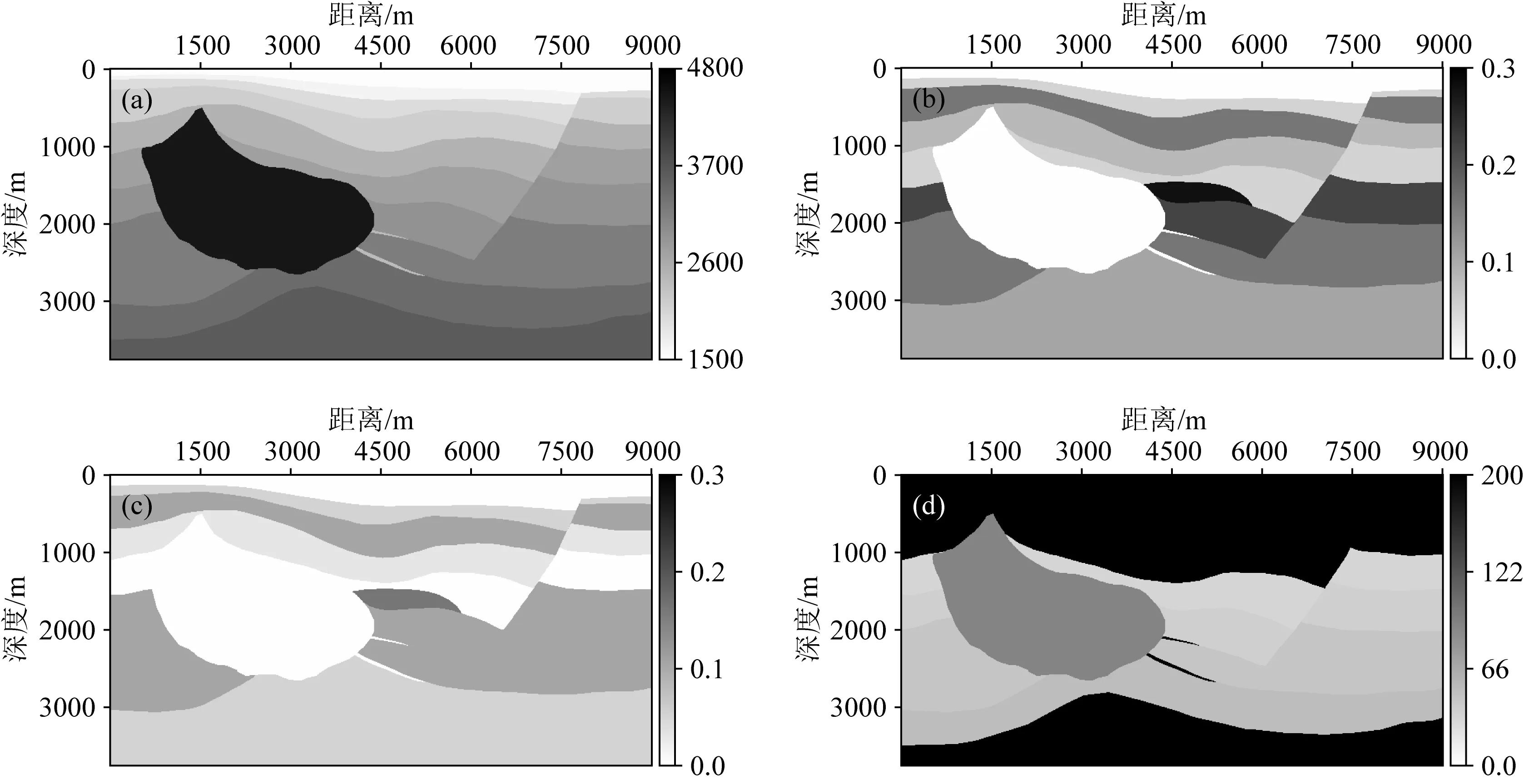
图5 VTI-Hess模型(a) 速度模型； (b) ε模型； (c) δ模型； (d) Q模型.Fig.5 VTI-Hess model(a) Velocity model; (b) ε model; (c) δ model; (d) Q model.

为了验证本文所推导的黏声各向异性波动方程在描述地震波衰减特征方面的准确性，分别进行声波各向异性及黏声各向异性数值模拟，图6为1.0 s及1.5 s时的波场快照对比.图7为VTI-Hess模型的声波各向异性单炮地震记录及黏声各向异性单炮地震记录对比.图8为使用不同方程模拟的单道(4500 m)地震记录及对应的振幅谱对比图.

图6 VTI-Hess模型数值模拟波场快照对比(a) 1.0 s纯qP波VTI； (b) 1.0 s黏声波VTI； (c) 1.5 s纯qP波VTI； (d) 1.5 s黏声波VTI.Fig.6 Snapshots of VTI-Hess model(a) Pure qP-wave VTI wave equation at 1.0 s; (b) Viscoacoustic VTI wave equation at 1.0 s; (c) Pure qP-wave VTI wave equation at 1.5 s; (d) Viscoacoustic VTI wave equation at 1.5 s.

图7 VTI-Hess模型数值模拟地震记录(a) 纯qP波VTI波动方程； (b) 黏声VTI波动方程.Fig.7 Records of VTI-Hess model(a) Record ofpure qP-wave VTI wave equation; (b) Record ofviscoacoustic VTI wave equation.

通过图6及图7中声波与黏声波数值模拟结果的对比可以发现，黏声各向异性的数值模拟结果中呈现出显著的振幅衰减及相位畸变，这说明文中推导的黏声各向异性波动方程在复杂介质中可以较好地描述地震波的运动学及动力学特征.从图8中的单道(4500 m)地震记录及对应的振幅谱对比可以看出，在黏声各向异性波动方程中，由于地层的吸收衰减作用，地震资料的能量减弱，主频降低，频带变窄，这会降低地震资料的分辨率.因此，必须对地震资料进行吸收衰减补偿逆时偏移.

图8 同一单道(4500 m)地震记录对比图(a) 单道记录对比图； (b) 单道记录振幅谱对比图.Fig.8 Comparison of single traces with different equation(a) Comparison between single traces; (b) Comparison between amplitude spectra of single traces.

为了验证黏声各向异性逆时偏移成像方法的效果，这里基于黏声各向异性数值模拟结果进行逆时偏移成像.图9为VTI-Hess模型偏移结果.由图可以看出，四种成像方法均可以对黏声各向异性地震记录进行成像.进一步对比可以发现，因未进行衰减补偿及忽略了各向异性，声波各向同性逆时偏移结果(图9a)中存在大量的构造假象，反射波难以准确归位，同相轴聚焦性不好，衰减区域难以成像，总体成像质量较差；进行了衰减补偿的黏声各向异性逆

图9 VTI-Hess模型偏移剖面(a) 声波逆时偏移剖面； (b) 黏声波逆时偏移剖面； (c) 各向异性声波逆时偏移剖面； (d) 各向异性黏声波逆时偏移剖面.Fig.9 Migration images of VTI-Hess model(a) Acoustic RTM; (b) Acoustic VTI RTM; (c) Viscoacoustic RTM; (d) Viscoscoustic VTI RTM.

时偏移结果(图9d)中的反射界面正确归位，绕射波得到较好收敛，断层、尖灭等复杂构造也得到精细成像，衰减区域成像清晰，分辨率更高，能量更均衡，成像质量较好.成像结果表明考虑介质各向异性及黏滞性影响可有效改善成像质量，提高成像剖面分辨率.

2.2 VTI-BP气云模型逆时偏移

为了进一步验证黏声各向异性逆时偏移成像方法在复杂模型及强烈衰减区域的适用性，本节利用具有强烈衰减气云构造的VTI-BP气云模型进行数值模拟及逆时偏移试验.图10为VTI-BP气云模型，模型大小为3970 m×1600 m，空间间隔Δx=Δz=10 m.共布设了79炮，起始炮点位于(35 m,10 m)，炮间隔为50 m.每一炮有401个接收点，平均分布在震源两侧，道间距为10 m.记录时间长度为2.0 s，时间采样间隔为0.5 ms.采用主频为30 Hz的Ricker子波作为震源函数.

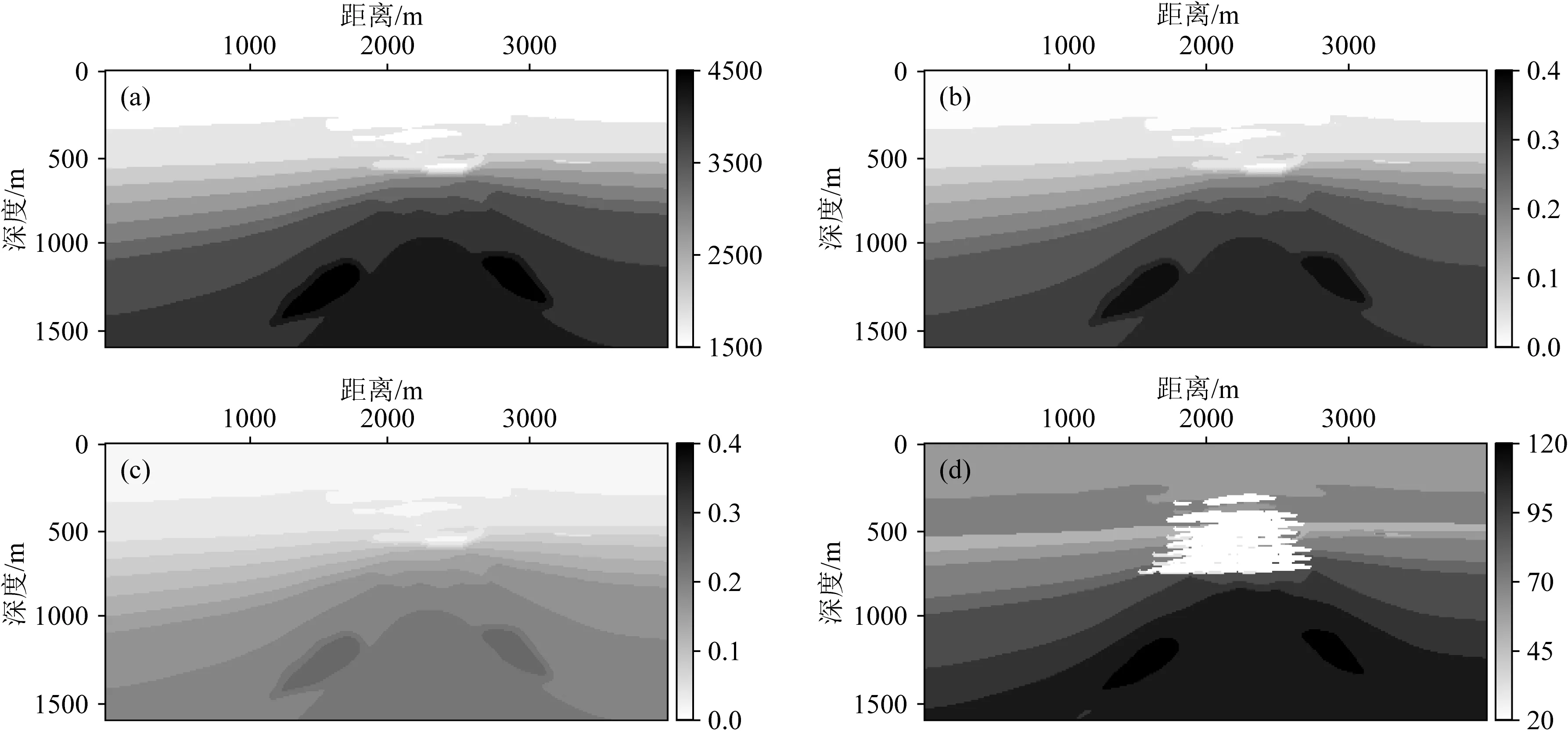
图10 VTI-BP气云模型(a) 速度模型； (b) ε模型； (c) δ模型； (d) Q模型.Fig.10 VTI-BP gas chimney model (a) Velocity model; (b) ε model; (c) δ model; (d) Q model.

图11是基于VTI-BP气云模型使用不同成像方法计算得到的0.5 s时震源波场及检波点波场对比图，其中左侧一列为震源波场快照，右侧一列为检波点波场快照.图11(a)和(e)中的波场是使用声波逆时偏移算法得到的，均未进行衰减补偿，波场能量较弱，由于未考虑各向异性，波前面的位置不准确；图11(b)和(f)中的波场是使用黏声各向同性逆时偏移算法得到的，经过衰减补偿的波场能量得到恢复，但在未考虑各向异性的情况下波前面位置不准确；图11(c)和(g)中的波场是使用声波各向异性逆时偏移算法得到的，图中波前面的位置准确，但因没有考虑衰减补偿的影响导致波场能量不均衡；图11(d)和(h)中的波场是使用黏声各向异性逆时偏移算法得到的，同时考虑了介质各向异性及衰减补偿因素的影响之后，波前面的位置准确，波场能量得到恢复.

图11 VTI-BP气云模型使用不同成像方法计算的震源波场及检波点波场快照(0.5 s)对比(a) 声波震源波场； (b) 声波检波点波场； (c) 黏声震源波场； (d) 黏声检波点波场； (e) 声波各向异性震源波场； (f) 声波各向异性检波点波场； (g) 黏声各向异性震源波场； (h) 黏声各向异性检波点波场.Fig.11 Snapshots at 0.5 s of source and receiver wavefields computed by different RTM of VTI-BP gas chimney model(a) Acoustic source wavefield snapshot; (b) Acoustic receiver wavefield snapshot; (c) Viscoacoustic source wavefield snapshot; (d) Viscoscoustic receiver wavefield snapshot; (e) Acoustic VTI source wavefield snapshot; (f) Acoustic VTI receiver wavefield snapshot; (g) Viscoacoustic VTI source wavefield snapshot; (h) Viscoscoustic VTI receiver wavefield snapshot.

图12是VTI-BP气云模型的偏移结果.图13为VTI-BP气云模型偏移结果在相同位置的局部放大对比图.在声波各向同性逆时偏移剖面中，因为未考虑各向异性及吸收衰减的影响，导致偏移剖面中存在大量成像假象，绕射波无法收敛，衰减区域难以成像，整体能量不均衡，同相轴较难聚焦.在黏声各向同性逆时偏移成像剖面中，虽然衰减区域的能量得到了一定补偿，整体能量更加均衡；但由于忽略了各向异性参数的影响，绕射波难以收敛，反射界面难以准确归位，剖面中存在成像噪声，部分同相轴连续性较差.在声波各向异性逆时偏移剖面中，绕射波得到收敛，反射界面位置也比较准确，但由于未进行衰减补偿，衰减区域的能量没有得到较好的恢复，深部反射界面的成像不够清晰，分辨率较低.而在黏声各向异性逆时偏移剖面中，绕射波得到充分收敛，反射界面得到准确归位，衰减区域能量得到恢复，同相轴的连续性和聚焦性更好，细小构造得到精细刻画，剖面的能量更加均衡，分辨率得到提高，成像质量更好.因此，黏声各向异性逆时偏移成像方法可以对衰减区域的能量进行补偿，对深部层位清晰成像，使绕射波得到归位，成像质量良好，偏移剖面分辨率更高.

图12 VTI-BP气云模型偏移剖面(a) 声波逆时偏移剖面； (b) 黏声波逆时偏移剖面； (c) 声波各向异性逆时偏移剖面； (d) 黏声各向异性逆时偏移剖面.Fig.12 Migration images of VTI-BP gas chimney model(a) Acoustic RTM; (b) Acoustic VTI RTM; (c) Viscoacoustic RTM; (d) Viscoscoustic VTI RTM.

图13 VTI-BP气云模型偏移剖面局部放大图(a) 声波逆时偏移剖面； (b) 黏声波逆时偏移剖面； (c) 各向异性声波逆时偏移剖面； (d) 各向异性黏声波逆时偏移剖面.Fig.13 Zoomed views of VTI-BP gas chimney model RTM images in Fig.10(a) Acoustic RTM; (b) Acoustic VTI RTM; (c) Viscoacoustic RTM; (d) Viscoacoustic VTI RTM.

2.3 TTI盐丘模型逆时偏移

通过一个盐丘模型进行TTI介质中黏声波的逆时偏移成像，从而证明所提出的黏声各向异性逆时偏移方法在复杂介质中的适用性及偏移效果.图14为TTI盐丘模型，大小为8000 m×3500 m，空间间隔Δx=Δz=10 m.共布设了141炮，起始炮点位于(500 m,10 m)，炮间隔为50 m.每一炮有601个接收点，平均分布在震源两侧，道间距为10 m.记录时间长度为3.5 s，时间采样间隔为0.5 ms.采用主频为30 Hz的Ricker子波作为震源函数.

图14 TTI盐丘模型(a) 速度模型； (b) ε模型； (c) δ模型； (d) θ模型； (e) Q模型.Fig.14 TTI-salt model(a) Velocity model; (b) ε model; (c) δ model; (d) θ model; (e) Q model.

图15为TTI盐丘模型的偏移结果.图16为TTI盐丘模型偏移结果(图15)在相同位置的局部放大对比图.从图中可以看出，因为未考虑各向异性参数及衰减补偿的影响，声波各向同性逆时偏移剖面中存在大量构造假象，反射界面位置不准确，剖面中能量不均衡，同相轴能量难以聚焦，剖面质量较低.黏声各向同性逆时偏移成像剖面中，在进行吸收衰减补偿之后，能量得到恢复，振幅较均衡；但由于忽略了各向异性参数的影响，绕射波难以收敛，反射界面不能准确归位，剖面中也存在一些成像噪声，部分同相轴连续性较差，分辨率较低.在声波各向异性逆时偏移剖面中，考虑了介质各向异性对偏移结果的影响，绕射波得到收敛，反射界面位置准确；但由于未进行衰减补偿，剖面的能量没有得到恢复，深部反射界面成像不够清晰.而在黏声各向异性逆时偏移剖面中，同时考虑了各向异性及吸收衰减补偿，绕射波得到充分收敛，反射界面得到准确归位，能量得到恢复，同相轴的连续性和聚焦性更好，分辨率得到提高，成像质量更好.因此，与其他成像方法相比，黏声各向异性逆时偏移可以对盐丘下方高速衰减区域清晰成像，无成像噪声，有效提高成像剖面质量.

图15 TTI盐丘模型偏移剖面(a) 声波逆时偏移剖面； (b) 黏声波逆时偏移剖面； (c) 声波各向异性逆时偏移剖面； (d) 黏声各向异性逆时偏移剖面.Fig.15 Migration images of TTI-salt model(a) Acoustic RTM; (b) AcousticTTI RTM; (c) Viscoacoustic RTM; (d) Viscoacoustic TTI RTM.

3 分析与讨论

3.1 成像方法的有效性和适用性分析

为了说明本文提出的基于黏声各向异性波动方程成像方法的有效性和适用性，本节基于VTI-BP气云模型，采用如下方程(Xu et al.，2015)进行数值模拟：

(24)

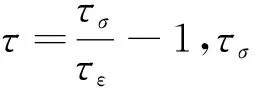
在进行数值模拟时，参数与2.2节中的参数保持一致.基于方程(24)的数值模拟结果，本节利用1.3节中的成像方法进行衰减补偿的偏移成像，并与2.2节中的黏声各向异性逆时偏移结果(图12d)进行对比.

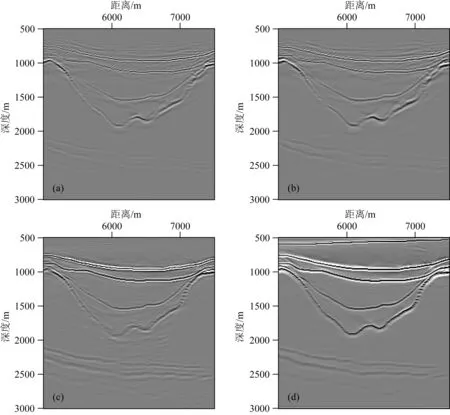
图16 TTI盐丘模型偏移剖面局部放大图(a) 声波逆时偏移剖面； (b) 黏声波逆时偏移剖面； (c) 声波各向异性逆时偏移剖面； (d) 黏声各向异性逆时偏移剖面.Fig.16 Zoomed views of TTI-salt model RTM images in Fig.13(a) Acoustic RTM; (b) Acoustic TTI RTM; (c) Viscoacoustic RTM; (d) Viscoacoustic TTI RTM.

对比图17中的偏移结果，可以看到基于方程(24)模拟数据的偏移剖面与基于本文推导的黏声各向异性波动方程模拟数据的偏移剖面一致，深层衰减区域的能量得到了恢复，层位构造清晰，证明了本文成像方法的有效性和适用性.

图17 VTI-BP气云模型黏声各向异性逆时偏移剖面(a) 基于方程(12)模拟数据； (b) 基于方程(24)模拟数据.Fig.17 Viscoacoustic VTI RTM images of VTI-BP gas chimney model using the synthetic data obtained with (a) equation (12) and (b) equation (24)

3.2 低通滤波器对偏移剖面质量的影响

在黏性介质中，由于需要在波场逆时延拓过程中对地震波吸收衰减进行补偿，地震波能量呈指数型增长，可能会放大不需要的频率成分，增加高频噪声，导致波场延拓的数值不稳定.为了避免这个问题，本文应用低通滤波方法切除高频噪声，滤波器的截止波数根据介质中最大速度上的截止频率计算得到.但这会使最终的偏移剖面损失一些有效的高波数成分，一定程度上会降低偏移剖面的精度.本节将对比不同滤波器参数下的偏移结果，以更直观地说明低通滤波器对最终偏移剖面质量的影响.

在现阶段的衰减补偿成像方法中，主要通过低通滤波器来保证波场延拓的稳定性，滤波参数的选取大多是依据经验进行取值.从图18中可以看出，当滤波参数过小或过大时，都会导致偏移剖面质量的降低.当低通滤波器的截止波数过小时，说明截去的高波数成分较多，会导致深层构造成像不清晰，降低成像剖面质量；当低通滤波器的截止波数过大时，表明截去的高波数成分较少，但无法保证波场延拓的稳定性，降低偏移剖面的精度.因此，在使用低通滤波器时，截止波数的选取一定程度上会影响衰减补偿偏移剖面的质量，这要求我们在今后的研究中寻找一种科学、定量的保持波场延拓稳定的方法.

图18 不同截止波数偏移剖面(a) 截止波数偏小(0.05)； (b) 截止波数适中(0.2)； (c) 截止波数偏大(0.35).Fig.18 Migration images of different cut-off wavenumbers(a) Low cut-off wavenumber (0.05); (b) Moderate cut-off wavenumber (0.2); (c) High cut-off wavenumber (0.35).

4 结论

(1) 本文在各向异性纯qP波动方程的基础上，结合常Q模型的松弛函数，推导出黏声各向异性纯qP波动方程.均匀模型数值模拟结果表明，该方程可以正确描述TI黏声介质中地震波的运动学及动力学特征，并且方程中的振幅衰减项与相位频散项解耦表示，便于在偏移过程中进行衰减补偿.

(2) 通过黏声各向异性逆时偏移成像结果可以看出，同时考虑介质各向异性及衰减补偿的成像结果可以较好恢复地下衰减区域的能量，使反射界面准确归位，绕射波得到收敛，增强同相轴的连续性和聚焦性，精细刻画细小的地质构造，剖面中能量得到均衡，提高剖面分辨率，成像质量更好.

(3) 本文通过低通滤波来保证波场外推时的稳定性，这会使最终的偏移剖面损失一些有效的高波数成分，一定程度上会降低偏移剖面的精度.因此，在今后的研究中可以进一步探讨上述问题.