利用深度学习的硬件计数器复用估计算法*

王一超，王鎏振，林新华

(上海交通大学 网络信息中心， 上海 200240)

硬件计数器是一组CPU专用寄存器。受限于芯片面积，主流X86和ARM CPU至多只能提供12个硬件计数器(C≤12)。在代码执行期间，硬件计数器会记录性能事件发生的数量，如浮点数计算指令数、缓存命中次数等。而主流X86和ARM CPU都提供了上百个硬件事件(E>500)。由于C远小于E，单次采集时，C无法覆盖所有的E。

为提高单次采集硬件事件的数量，许多常用的性能分析工具如PAPI[1]、HPCToolkit[2]等提供了硬件计数器复用(multiplexing，MPX)功能。MPX包括数据采集和结果估计两大步骤：首先，MPX以一个固定频率读取硬件计数器实际采集到的硬件事件数据；其次，MPX基于估计算法，填补未被实际记录的数据。这样MPX就能在单次采集中使用少量硬件计数器C采集大量硬件事件E。基于MPX采集大量的硬件事件数据，研究人员可对应用在CPU上的性能表现进行深入的量化分析[3]。因此，性能分析工具中的MPX对于性能建模研究具有重要价值。

然而，目前PAPI MPX[1]仍采用数值拟合方法补齐未实际采样部分，例如固定插值[4]、线性插值[5]及非线性插值[6]。而这些数值拟合方法的精度较低，主要有两个原因：①基于数值拟合的估计算法无法准确预测所有事件的发生情况，因为一个硬件事件在不同CPU上运行不同程序时，并不服从任何特定随机过程；②采用数值拟合方法的MPX可以提升部分事件的采集精度，但有些事件精度过低，甚至出现负增益，导致MPX结果置信度偏低。事件数量的估计准确度对MPX模式下取得的结果，起到至关重要的作用。根据之前工作的评估[3,6]，当MPX估计算法的准确性下降到90%以下时，数据将无法被用于性能建模。

为提升MPX结果精度，利用深度学习方法，基于神经网络多层感知器[7](multilayer perceptron，MLP)和双向门控神经网络[8](bidirectional gated recurrent unit, Bi-GRU)2个模型，为MPX提供置信度更高的估计模型。需要说明的是，本文研究的MPX方法面向高性能计算中常用的性能事件，在程序单核运行阶段，对于多事件进行采样，从而得到可以用于性能建模的大量性能事件。

为了使模型提取到的特征可以覆盖高性能计算的主流应用程序，选取了在高性能计算领域主流的Rodinia测试集[9]。该测试集中的应用覆盖了13类典型的高性能计算应用，基于该测试集的数据进行训练，可以有效提升模型在高性能计算领域的泛化能力。

1 研究背景及相关工作

1.1 MPX基本原理

MPX采用分时复用方法，将各个硬件计时器的可用时间切分成不同时间片，然后在不同时间片上轮流记录不同硬件事件。具体包括两个步骤：

1)数据采集。MPX以一个固定频率，读取硬件计数器实际采集到的性能事件数据，写入内存中。

2)结果估计。由于硬件计数器在多事件调度过程中，存在部分事件发生次数未被计数器记录的情况。因此，MPX需要基于估计算法估出该时间段内事件发生的次数，补全未采集到的数据。与MPX相对的是使用单一寄存器记录单一事件(one counter one event，OCOE)，这种采集数据的精度高，但单次采集硬件事件受限于硬件计算器数量(C≤12)。

1.2 MPX估计算法使用的数值拟合方法

已有MPX估计算法都采用了数值拟合方法。根据采用的方法不同，可分为三类：

1)固定插值法。2001年，May[4]在PAPI[1]上开发了面向性能监控单元(performance monitor unit, PMU)事件的多路复用技术，即PAPI默认MPX实现。该实现基于固定时间片调度和固定插值的估计方法，如图1(a)所示，本文将该方法作为基准比较对象。

2)线性插值法。2005年，Mathur等[5]量化了由MPX引起的误差，设计了4种插值估计算法，包含梯形面积法等，如图1(b)所示，采用线性插值法替换固定差值法，提升了估计精度。实验数据表明[10]，线性插值法会造成42%的估计值比实际值大10%以上，其中误差在 50% 的估计值最高占比达29.3%。

3)非线性插值法。本文作者对文献[4]的工作进行了改进[6,11]，提出采用非线性插值替换线性插值的估计方法，如图1(c)所示。

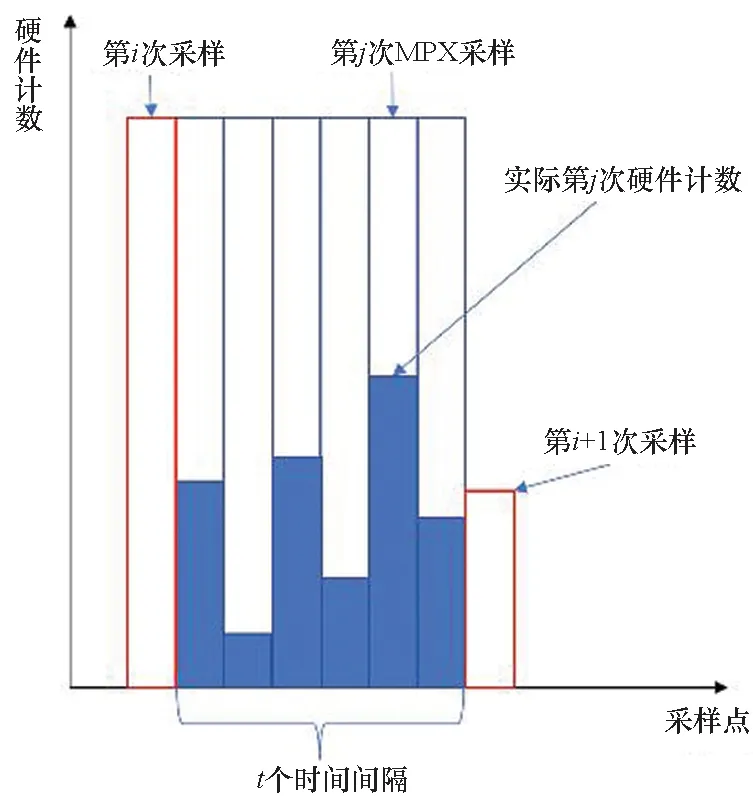
(a) 固定插值法 (a) Fixed interpolation

上述三种方法都受限于数值拟合的局限，结果精度仍有进一步提升的空间。有不少基于硬件事件的性能建模研究工作采用了深度学习方法作为拟合手段[12-14]。受此启发，为进一步提升MPX估计精度，本文采用深度学习方法进行MPX估计。

2 数据清洗与相关性分析

在对数据进行相关性分析之前，需要先对数据进行清洗，以修正一些明显异常的值，从而提高数据分析的准确性。数据出现明显异常的原因有两种：一种是性能分析工具如PAPI在采集时出现异常；另一种是由于MPX估计算法不能及时判断程序结束而导致的。以分支预测未命中的硬件事件BRMIS:ALL为例进行说明。

2.1 变量定义

首先对下文使用到的变量做如下定义：

1)Sampledi表示i时刻MPX采集到的硬件计数；

2)Counti表示i时刻估计算法给出的硬件计数；

3)Interval表示两次采样之间的时间差。

其中，Interval由MPX同时采样的硬件事件数量Event_num以及OCOE模式下最大支持的可编程硬件计数器数量Counter_num决定，即：

(1)

PAPI默认的MPX采用固定插值法，即假设同一时间片内硬件事件发生的次数保持不变，将采样间隔内某一时刻采集到的硬件计数值进行固定插值，即：

Countedi=Sampledi×Interval

(2)

2.2 数据清洗：异常值处理策略

PAPI在采集时出现异常值，主要有以下两个原因：

1)性能分析工具没有采集到任何硬件事件或是硬件计数出现负值。这部分异常是由于PMU异常溢出导致的，使用MPX和OCOE均有一定概率出现该现象。实验表明，所有未出现异常计数的采样得到的硬件计数和均小于0.3×Countmax。因此针对这部分异常，本文根据采集到的硬件计数和设置了一个阈值：记硬件计数和的最大值为Countmax，将所有硬件计数和小于0.2×Countmax的采集舍弃，确保使用的数据都是有效采集的。其中，选择0.2为系数是因为采样无法保证能检测到所有情况，因此适当降低阈值避免错误地将正常采样归为异常采样。

2)采集到的硬件计数图像中存在异常值。图2显示的是在Intel Xeon Gold 6248上对Rodinia测试集中的StreamCluster[9]采集到BRMIS:ALL的硬件计数-时间步图像，异常值部分是硬件计数-时间步图像中出现的异常偏低点，使用蓝色矩形块框出。这一现象在文献[14]中曾提到过，可采用K最近邻(K-nearest neighbor, KNN)法神经网络修复。由于异常值产生的原因有很多，无法准确判断是由性能分析工具本身的不稳定还是在程序运行中出现问题而导致的。因此针对这部分异常，本文采取保留异常值的策略。

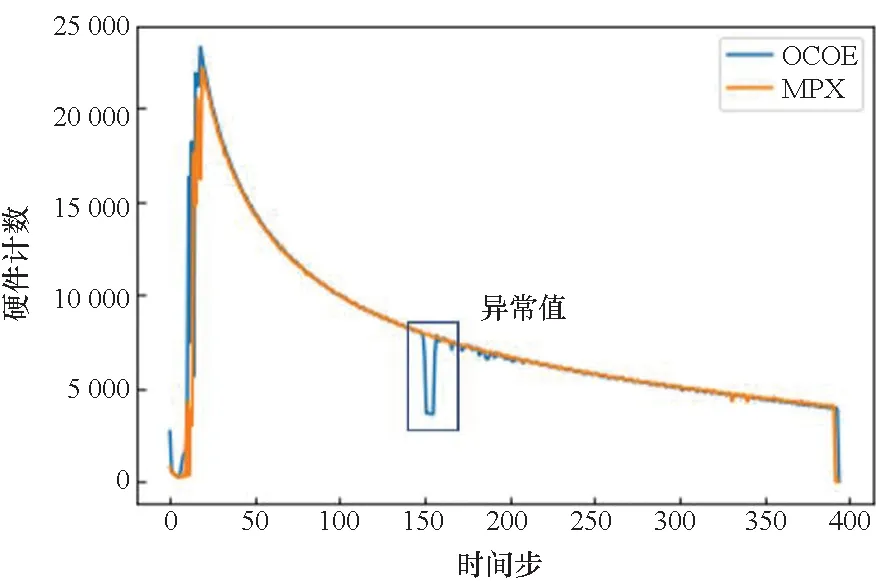
图2 在Intel Xeon Gold 6248上对StreamCluster采集BRMIS:ALL产生的异常值Fig.2 Outlier of BRMIS:ALL event counts when sampling of StreamCluster benchmark on Intel Xeon Gold 6248

2.3 数据清洗：尾部截断

如图3所示，对比OCOE和MPX固定插值这2种模式下的事件计数结果，可以看出两者结果已比较接近。然而通过放大数据图的尾部，可以发现当OCOE下硬件计数已经归0时，MPX下仍在基于估计算法填充缺失的数值，导致这部分计数结果与实际情况发生偏差。

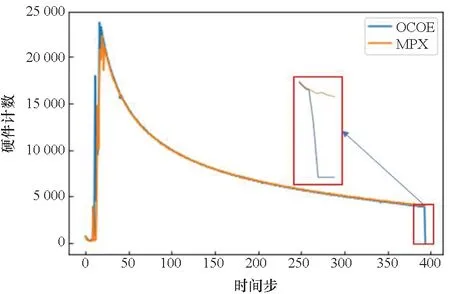
图3 采用OCOE和MPX固定插值2种模式得到的BRMIS:ALL事件计数结果对比Fig.3 BRMIS:ALL count/time step curve under two modes

以上现象是由于处理器性能波动引起的，同一程序即使在相同运行参数下，在同一个处理器上每次运行的时间会有差异，这导致了在程序运行的末尾，每次运行的结果差异较大。因此，为提高MPX结果精度，应把程序临近结束的部分予以截断。本文选取的截断方式是舍去采样步长的末尾2%。考虑到部分硬件事件采集到的时间片数量较少，因此在舍弃末尾2%的基础上进一步舍弃末尾5个时间步的数据。尾部截断后，重新计算得到的BRMIS:ALL在OCOE与MPX模式下，计数结果的曲线重合度显著提升。

2.4 数据相关性分析

对比图2和图3，可以观察到以相同参数运行同一程序，不同采集方式得到的硬件计数-时间步图像有着较高的相似度。为验证这一发现，本文采用皮尔森相关系数[15]衡量两者之间的相似程度。皮尔森相关系数是一种用于衡量两份数据线性相关程度的指标，其范围在-1到1之间，相关系数绝对值越接近1，相关度越强。负的相关系数则表示两者负相关。具体计算公式为：

(3)

通过计算，两次采集到的BRMIS:ALL硬件计数之间的皮尔森相关系数为0.93。进一步计算其他许多硬件计算器的数据，结果也类似。这证明在相同参数下，多次运行同一程序而得到的硬件计数值具有极高的线性相关性。这个发现是本文采用深度学习方法拟合MPX估计算法的理论依据。

与本文的这个发现不同，以往基于数值拟合的MPX估计算法都是基于时间局部性的假设，即认为相邻时间片内由于时间相关性，必然存在一定关联，并据此设计MPX估计算法。如固定插值法[4]认为相邻时间片硬件事件数量相等，线性拟合法[5]假设相邻时间片间硬件计数呈连续或离散的线性关系，而非线性拟合法[5]假设相邻时间片间硬件计数成连续或离散的指数关系。

3 深度学习模型的选取与训练

基于上述发现，考虑到硬件事件发生具有时序性的特征以及拟合的泛用性，选取深度学习中的MLP和Bi-GRU模型，以MPX采集到的数据为自变量，OCOE采集到的数据为因变量，构建从MPX数据到OCOE数据的函数映射。具体而言，MPX的输入是一个长度为t的序列：[Sampled_1,Sampled_2,…,Sampled_t]，在经过深度学习模型进行一系列矩阵或向量相关运算后，输出一个长度同样为t的序列：[Predicted_1,Predicted_2,…,Predicted_t]。

3.1 MLP模型的参数设置与模型结构

MLP[12]是经典的深度学习模型，与最小二乘法寻找拟合函数的原理类似。MLP可以通过最小化均方误差训练出一个能将MPX数据映射到OCOE数据的模型。考虑到硬件事件时序数据没有高维特征，不需要过多的隐含层数。模型超参数选取如表1所示，模型结构如图4所示(图中圆圈表示神经元)。由于数据集较小，MLP模型中每个隐含层的神经元都有30%的概率失效，添加了Dropout=0.3避免过拟合[13]。

表1 MLP模型超参数

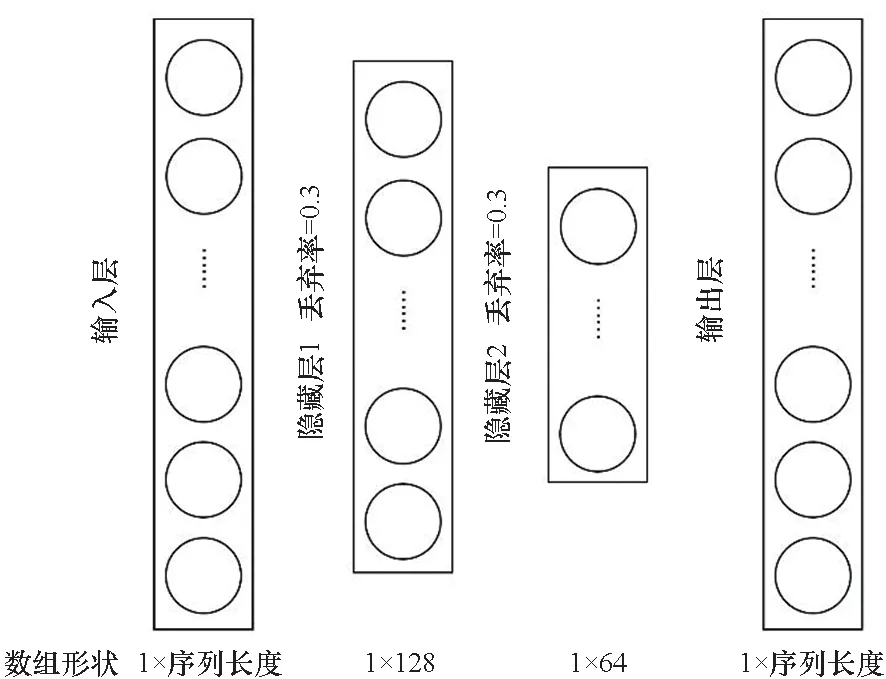
图4 MLP模型示意Fig.4 Illustration for MLP model

3.2 Bi-GRU模型的参数设置与模型结构

Bi-GRU是双向长短期记忆神经网络(bidirectional long-short term memory，Bi-LSTM)[8]的简化。Bi-GRU是循环神经网络模型中的一种，针对时序数据问题训练效果出色。其中LSTM[15]引入了遗忘门，解决了循环神经网络(recurrent neural network, RNN)在长时依赖下的梯度爆炸和梯度消失问题，而GRU[16]在保持LSTM效果的前提下对网络结构进行了精简，将遗忘门和输出门合并为更新门，有效缩短了训练神经网络所需时间。而双向意味着将时间序列按正反双向输入网络，使得输出某一时刻结果时可同时参考上下文信息。

控制模块采用单片机STC89C52控制。STC89C52与DDS信号产生模块进行串口通信，通过软件的编程，实现对输出波形的控制。外围电路采用独立按键的方式，可以选择波形种类的输出以及调节频率、电压幅度的大小。该电路通过P4.0、P4.1、P4.2、P4.3 接口与信号发生部分的 CS、SDATA、SCLK、FYSYNC 接口相接；通过 P3.0～P3.7和P1.7接口与按键电路连接；通过P0.0，P0.1，P0.2接口与显示电路连接。最后通过软件的编程，来对各部分电路进行控制。

考虑到程序运行时记录的硬件事件就是一个标准的时间序列，而且程序运行时的上下文切换也会对硬件计数造成影响，采用Bi-GRU来处理MPX估计。模型参数选取如表2所示，结构如图5所示。

表2 Bi-GRU模型参数

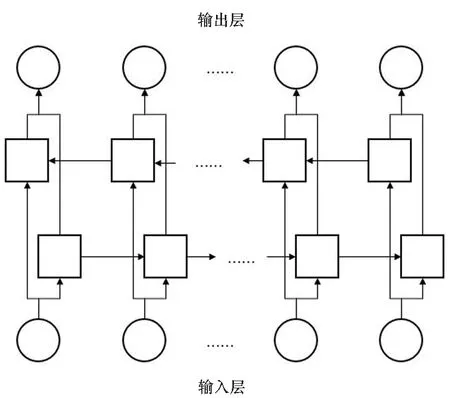
注：正方形表示GRU单元，圆圈表示序列中的数据点。图5 Bi-GRU模型示意Fig.5 Illustration for Bi-GRU

3.3 生成训练所需的数据集

实验在Intel Xeon Gold 6248上使用基于PAPI v5.7.0开发的NeoMPX[17]进行硬件事件采样，选取Rodinia 测试集[9]的13个应用，每个应用分别通过MPX和OCOE采集到15个硬件事件。

生成训练数据集需要5个步骤：①MPX运行1次应用即可采集到15个硬件事件，而OCOE需重复运行应用3次，所有应用的运行参数均按推荐值设置；②对每个应用，实验将重复运行4x次，其中x次以MPX方法进行采样，而另外3x次以OCOE方法进行采样(x>100)；③对采集到的结果均进行尾部截断(见2.3节)，并通过设定计数总和阈值进行筛选，最终得到总量为100份的MPX和OCOE采样结果；④每一份采样结果包含一个时序序列，其中的采样数据量大约在200～700个硬件事件值；⑤实验将这100份结果打乱后，以7 ∶1 ∶2的比例按序号随机切分成训练集、验证集及测试集，集合两两之间没有重复元素。

3.4 模型训练步骤

使用Pytorch v1.6.0实现MLP及Bi-GRU模型，输入为70份MPX和OCOE采样结果，输出为经MPX估计后的结果。模型训练的关键步骤如下：

1)数据大小预处理。由于MPX与OCOE采样数据量庞大，通常在107量级，直接拟合效果不佳，因此需要对数据进行对数化处理，取对数底为10。

2)数据长度预处理。由于溢出时间的不确定性导致结束位置不同，所以数据尾部的2%会被截断；同时考虑有的硬件事件发生的时间片较短，因此在此基础上舍弃最后5个时间步的数据。

3)模型训练。以MPX采集到的数据为自变量，OCOE采集到的数据为因变量，将它们组合成Tensor data的格式，通过Data Loader，以batch_size=1的大小将数据输入2个模型中。计算完均方误差后反向传播至神经网络各神经元中。将所有训练集中数据输入进神经网络后完成一个epoch。重复上述过程完成模型训练。

5)结果验证。对测试集中的20份数据分别依照评价标准计算模型得分，并根据这20份数据的平均值进行评价。

4 实验配置与评价指标

4.1 实验配置

1)实验环境。实验硬件为Intel Xeon Gold 6248 CPU，软件是基于PAPI v5.7.0开发的NeoMPX[17]。

2)测试算例。为全面考察MPX估计算法在高性能计算应用中的使用效果，选取13个来自Rodinia的测试程序，如表3所示。这些测试程序涵盖了高性能计算中5种不同计算模式及9个不同应用领域。

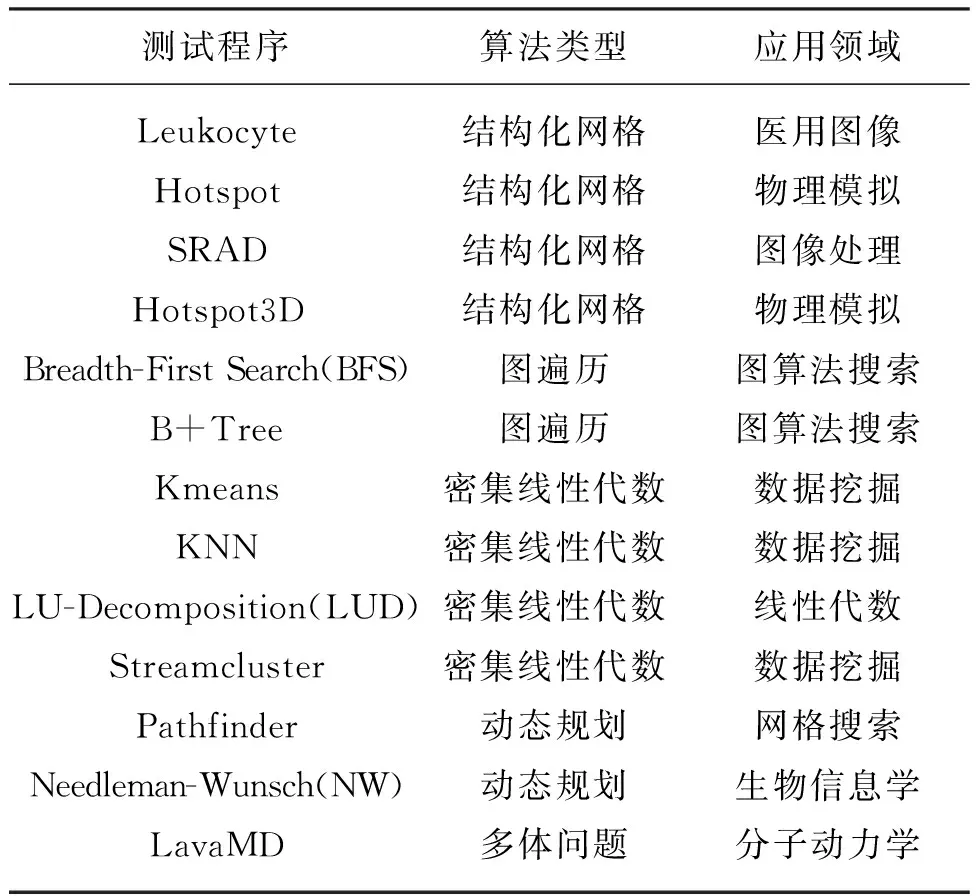
表3 13个Rodinia测试程序

3)硬件事件。主流CPU能够支持的硬件事件多达上百个，但性能检测与分析中常用的事件并不会全部用到。因此，本文选取了15个性能分析与建模中比较常用的硬件事件，如表4所示。这些事件涵盖了缓存访问、TLB访问、内存访问以及分支指令。要采集这15个事件，MPX只需运行1次，而OCOE需运行多次。

4.2 评价MPX结果精度的指标

为准确评价MPX结果精度，本文提出2个指标。

表4 15个用于评估的硬件事件

1)相对精度(relative accuracy，RA)。该指标参考了统计学中相对误差的概念，计算公式如下：

(4)

其中，MPXi和OCOEi分别代表第i个时间步时，MPX的结果以及使用OCOE模式采集到的硬件计数。式中减数即为统计学中的相对误差。为更直观反映MPX估计算法的好坏，用1减去相对误差得到RA值。RA值越高，表明由MPX估计算法得到的结果越接近于OCOE采集到的结果，即精度越高。

2)时间序列间的相似度[18](dynamic time warping，DTW)。假设MPX数据为MPX1,MPX2,…,MPXm；OCOE数据为OCOE1,OCOE2,…,OCOEn。DTW算法首先计算所有MPXi到OCOEj的欧氏距离，从而得到一个m×n的二维矩阵。将该二维矩阵视为一个网格，网格上所有的值代表经过该点的开销。最后需要求得一条通过该矩阵网格的最优路径。该路径有如下限制：

1)从(1, 1)开始，到(m,n)结束；

2)若前一个点选择了(i,j)，下一个点只能在(i+1,j),(i,j+1),(i+1,j+1)中选择。

该路径可以通过动态规划算法得出，DTW-cost为该路径上的开销总和，它表示MPX序列中元素到OCOE序列中最近的邻近元素累计距离之和，其值域为[0,+∞)，该值越小，说明两序列越相似。

DTW-cost有效避免了欧氏距离衡量两个时间序列中，由于序列间的相位延迟、长度不匹配等造成的评估结果与实际表现不匹配的问题。

5 实验结果

为确定测试重点，本文测试了PAPI默认的固定插值MPX在15个硬件事件上的效果，即硬件事件在13个应用上的平均RA分数，结果如图6所示。固定插值MPX在8个硬件事件上的平均RA分数超过了0.85，因此结果分析重点关注余下6个RA分数低于0.8的硬件事件。

图6 默认估计算法得到的不同硬件事件平均RA分数(越高越好)Fig.6 Average RA score on different hardware event gained by PAPI default method (higher is better)

表5从应用维度对比了固定插值MPX与基于MLP模型的MPX结果。后者在所有Rodinia测试集中12个应用的平均RA分数都得到了提升。以SRAD为例，MLP方法相比固定插值MPX提升了27.4%，从原先的0.73提升到0.9以上。

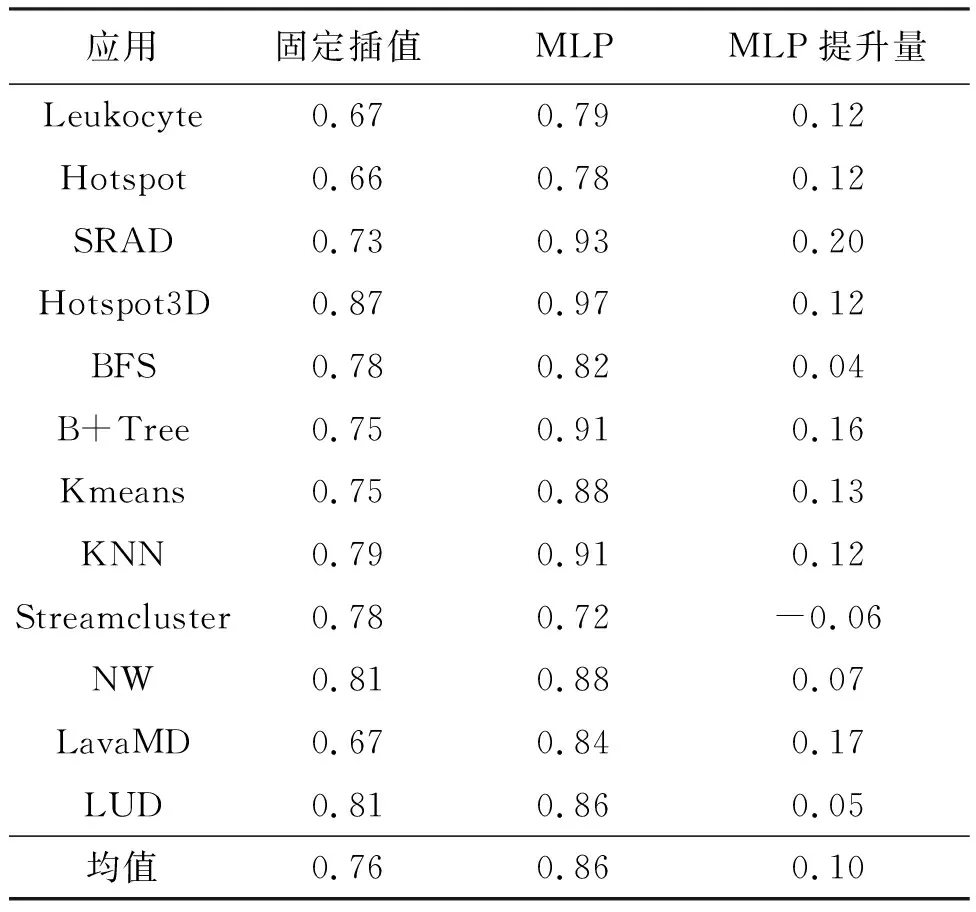
表5 不同应用的平均RA分数对比(越高越好)

需要指出的是，考虑到出现负值说明预估的硬件计数要比实际硬件计数高出一倍以上，因此负值是无意义的。为不产生误解，负值将被处理为0后再做比较。如表5所示，重新计算了两种方法在各应用上的平均RA分数，经修正后的MLP得到的RA分数比默认方法高出0.10，相比默认的方法提升了13.16%。其中最大提升幅度出现在SRAD应用上，达到了0.20。

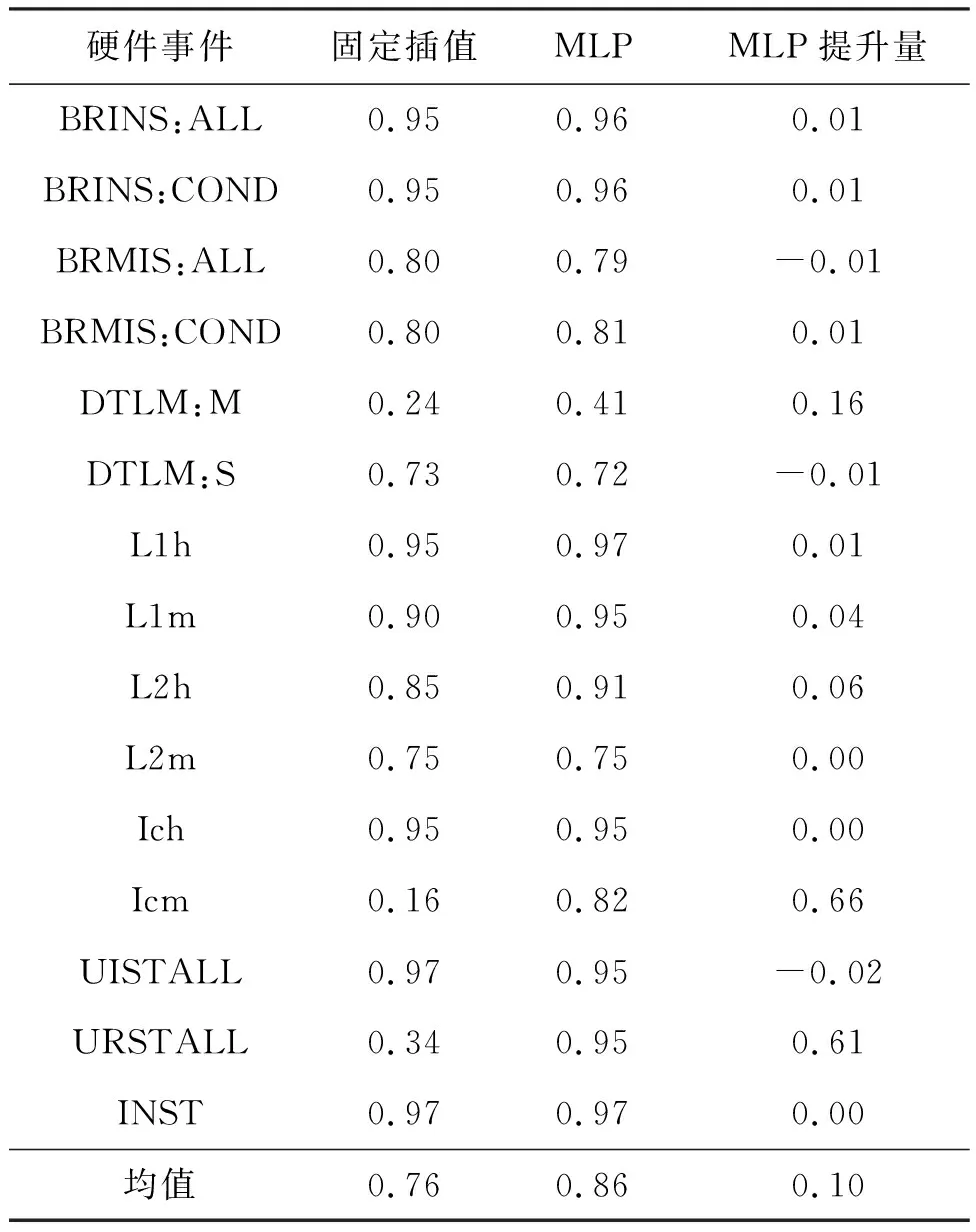
表6 硬件事件平均RA分数对比(越高越好)

表6从硬件事件的维度，对比了固定插值MPX与基于MLP模型的MPX结果。实验结果表明，在固定插值MPX达到较高RA的硬件事件上，MLP能取得相近表现，至多相差0.01。而MLP相比固定插值的最大提升是在Icm、URSTALL这两个硬件事件上，分别提升了0.66和0.61，将原本无法用于实际场景的硬件事件的RA分数提升到0.82甚至0.95的可信度水平。

如图7所示，本文使用DTW指标评判固定插值MPX与基于MLP模型的MPX结果。参考表6与图7结果，从总体上来说，RA与DTW两种评价指标基本一致，即RA越高，DTW-cost越小，MPX结果精度越高。

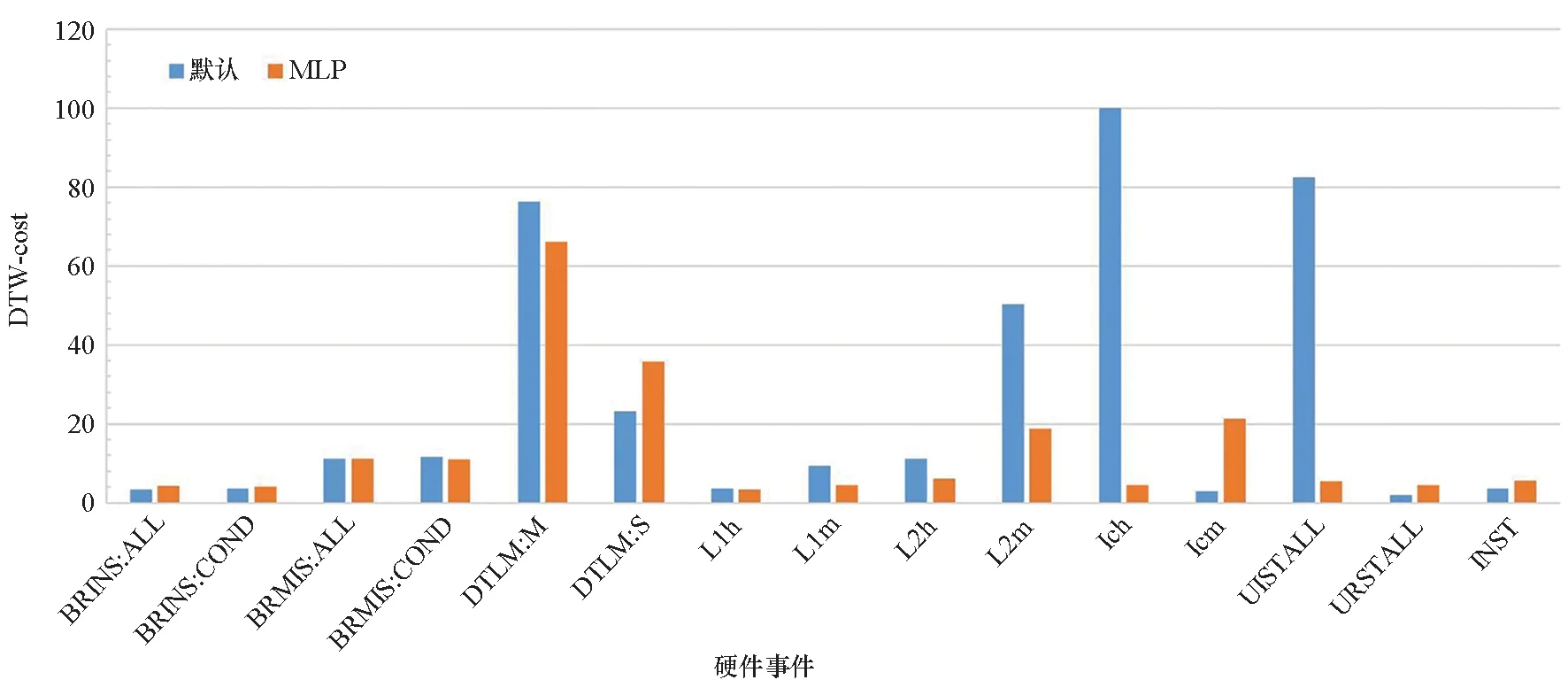
图7 默认方法与MLP方法的DTW开销对比(越低越好)Fig.7 DTW cost comparison between default method and MLP method (lower is better)

对于采用固定插值MPX就能达到RA 0.9以上的硬件事件，MLP能够达到相近精度，但已没有进一步的提升空间。因此，对Bi-GRU效果的评估只考虑原本效果较差的那些硬件事件。RA分数对比结果如图8所示。

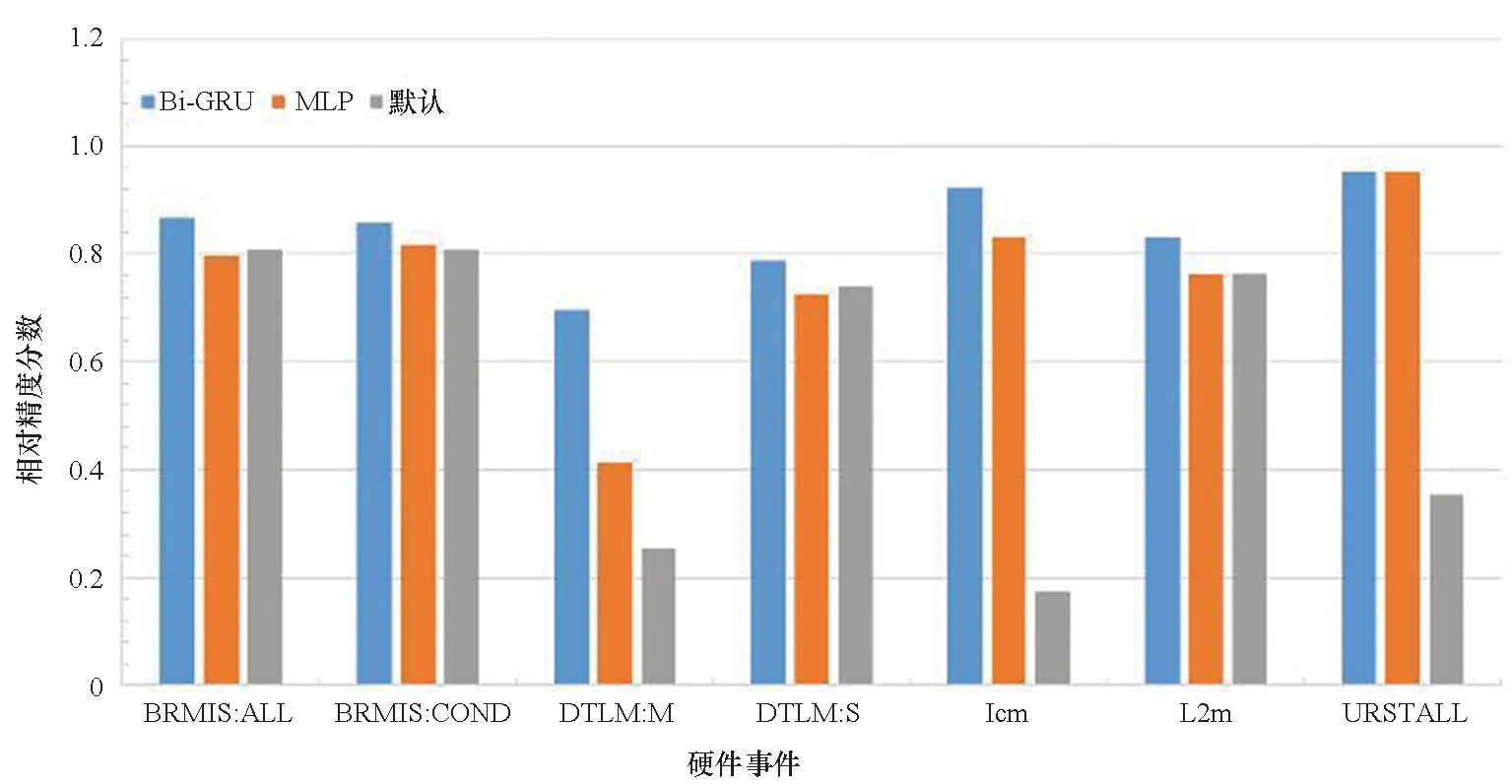
图8 三种估计算法RA分数对比(越高越好)Fig.8 RA score comparison among three estimation methods(higher is better)

针对选取的7个硬件事件，Bi-GRU取得了最好的效果，其次是MLP，两者皆优于固定插值MPX。对于这7个硬件事件的平均RA分数，Bi-GRU相比MLP提升了0.09；相比固定插值MPX提升了0.29，其中最大提升0.75，最小提升0.05。这表明Bi-GRU对于具有时间序列特征的硬件事件具有较好的效果。

如图9所示，本文使用DTW-cost指标对Bi-GRU算法进行评估。除DTLM:S的DTW-cost与RA表现相反以外，其余硬件事件均符合DTW-cost越低，RA越高的规律。其中，Bi-GRU模型取得了最低的DTW-cost，7个硬件事件的DTW-cost均值为20.86，相比MLP模型的24.42降低了14.58%。而MLP和Bi-GRU这2种基于深度学习方法的DTW-cost相比于数值拟合方法(50.60)分别降低了51.74%和58.77%。

图9 3种方法的DTW开销对比(越低越好)Fig.9 DTW-cost among three methods (lower is better)

6 结论

为进一步提升精度，本文基于深度学习模型MLP和Bi-GRU，提出了2种新的MPX估计算法。本文的MPX实现旨在面向高性能计算应用，在处理器性能建模中，提升关键硬件事件的多事件采集精度，进而为性能建模提供更可靠的大数据基础。本文主要有以下3个贡献：

1)通过MPX结果与实际数据的相似性分析，证明多次运行之间得到的硬件计数值存在线性相关性；

2)基于MLP和Bi-GRU深度学习模型，对MPX结果估计进行数据拟合，提升了MPX结果精度；

3)基于时序分析提出评估MPX结果准确度的指标。

实验结果表明，基于MLP和Bi-GRU模型的MPX估计算法都能有效提升MPX结果精度。在Intel CPU上运行的13个基准测试程序中，在同时记录15个硬件事件时，MLP模型相比固定插值MPX，RA分数平均提升了0.10左右，最多能提高0.66。而在MLP模型提升有限的7个硬件事件中，Bi-GRU模型相比固定插值MPX提升了0.288，其中最大提升达0.745。使用DTW-cost进行评估时，两种基于深度学习的模型均比固定插值法降低了超过一半的DTW-cost。对比本文之前的工作，在更广泛的高性能计算应用中(由6个拓展到13个)取得了更好的表现。此外，实验结果表明，对于固定插值法下估计精度较差的硬件事件，采用MLP和Bi-GRU方法后，取得了更高的精度。部分硬件事件的精度在MLP和Bi-GRU方法下，精度仍未达到0.9，说明目前模型在面向不同硬件事件时，其模型的泛化能力仍有待评估与研究。

未来的工作将对MPX模式下的异常值产生机制和性能波动原因深入分析，从而降低由于意外波动导致的误差。后续还将增加MPX同时采集的硬件事件数量，并将更多常用硬件事件纳入硬件事件组，从而验证基于深度学习的模型拟合方法在硬件事件更多、时间片更短的情况下，是否能够达到提升RA分数的效果，并最终在多核处理器上实现多线程并行抓取。