波浪作用下水下航行体出水成功概率预报*

孙龙泉，任泽宇，李志鹏，马贵辉，赵建洲

(哈尔滨工程大学 船舶工程学院， 黑龙江 哈尔滨 150001)

潜射导弹发射技术中，对潜射导弹在不同的海浪环境下出水姿态参数的预报至关重要。潜射导弹点火技术主要分为两类：①导弹发射一段时间后在水中点火；②导弹出筒后依靠惯性在水中航行，离开水面时点火。对于水面点火的水下发射方式，如果出水姿态参数不够理想，导弹出水后的二次推进就无法调整弹体的轨迹，甚至会影响到潜射导弹的成功出水，因此预报在波浪作用下导弹出水的姿态参数对导弹的成功发射有着至关重要的作用。而实际中波浪的运动是非常复杂的，不同浪向、频率的波浪相互叠加造成了波浪属性的随机性，所以实现实测波浪下水下航行体出水成功的预报更有实际的意义。

水下航行体出水过程中受到波浪的扰动，二者之间的作用属于流体与固体之前的相互耦合作用，流固耦合数学模型主要包括理想势流模型和NS模型。由于NS模型具有耗时以及大幅度运动过程中网格易发生严重变形等缺点，本文的计算模型采用理想势流模型。倪宝玉[1]、Longuet-higgins等[2]就理想势流模型的可行性做出了详细的论述和验证，使在忽略黏性等因素后的数学模型得到了大大简化，提高了计算效率。对于理想势流模型的求解，目前的主要求解方法包括边界元方法和有限元方法。李帅[3]、Li[4-5]、Kashiwagi[6]等使用边界元方法求解，Eatock[7]、Ma[8]等采用有限元方法求解。

然而，在水下航行体出水计算过程中，结构湿表面网格的重新布置以及自由面非线性边界条件的处理都显得十分复杂。为了解决这一系列复杂问题，Ma[8]和Yan[9]等使用QALE-FEM方法，在整个出水计算过程中只生成一次复杂的结构化网格，在下一时间步直接计算到边界位置，大量节省了网格重置的时间。倪宝玉[1]提出在水下航行体出水过程中，由于其高速运动，流场可以近似认为是准静态流场，可以绕射理论为基础，采用势流理论计算方法解决水下航行体出水问题。Xue[10]、Miloh[11]等就自由面非线性边界条件的问题，进行了计算模型和边界条件的简化，并与试验对比进行了有效性验证。

在水下航行体弹道计算方面，李代金[12]、李体方[13]等对航行体发射过程中弹道的数学模型进行了建立和分析，这些数学模型可用于潜射导弹等水下航行体的弹道计算，也为其他弹道模型的建立提供了参考依据。刘曜[14]、姜涛[15]通过解析法计算了水下航行体受到波浪作用后所受载荷大小，并且通过轨迹方程得到了水下航行体运动姿态变化。王红萍等[16]以自建的高精度数值波浪水池为基础，探究了波浪扰动力以及运动姿态参数的变化规律，为后续的弹道设计打下基础。尤天庆等[17]针对航行体尾空泡对流体阻尼力影响的问题，通过求解雷诺平均的斯托克斯方程组，进行阻尼力计算研究，验证了弹道设计中考虑尾空泡的重要性。后续研究发现在航行体表面进行通气可以改善航行体表面的流体动力特征，从而提高水下航行体的出水成功概率。例如：刘涛涛[18]、王克林[19]等对气孔排气的气液两相流特性进行了研究，为排气孔的设计优化提供了参考；马贵辉[20]、张耐民[21]就通气空泡技术改善航行体水下弹道及出水姿态参数的有效性和可行性做了详细论述。

综上所述，虽然国内外的科研人员对水下航行体出水问题已经做了很多研究，但是大多需要借助计算流体力学(computational fluid dynamics, CFD)相关的商业软件，计算时间长、工作量大，没有办法形成规模计算，对海浪和水下航行体相互作用的定性分析也存在困难,同时，缺少在实时海况下的水下航行体出水成功概率的快速预报，在此方面无法为潜艇作战提供帮助。本文以边界元方法，在波浪和水下航行体的流固耦合分析上做了一定程度的改进，大大缩短了计算时间，并且将计算结果纳入规则波浪数据中，以此为基础，能够在一定程度上实现实时海况下的航行体出水成功概率预报。

1 理论与方法

航行体在水下运动时，所受到的重力、浮力、流体力会影响水下航行体的原始轨迹并发生偏离。出水姿态参数是影响航行体出水成功与否的重要因素之一，如果出水弹道设计不好，潜射导弹出水后具有的角速度或偏转角可能会超出允许的控制范围，无法通过水面点火等方式调节平衡，从而直接导致发射失败[22]。本文主要以俯仰角为例，研究波浪参数对尾部触水俯仰角的影响，并且以尾部触水俯仰角为判定依据进行水下航行体出水成功概率的预报。水下航行体运动姿态的示意如图1所示，俯仰角φ为航行体轴线和水平方向的夹角。

图1 水下航行体运动轨迹Fig.1 Trajectories of underwater vehicles

如图1所示，小尺度航行体在水中高速运动时，雷诺系数很大，惯性力的影响远大于黏性力的影响[1]，所以对水下航行体的数学模型做简化，能够实现规模计算。弹体在水下运动的数学模型简图如图2所示，航行体发射时有垂直向上的初始速度，同时加入了水平艇速的影响，上升过程中主要受到重力、流场惯性力和波浪力的作用。

图2 弹体出水坐标系Fig.2 Projectile body outlet coordinate system

如图3所示，以半球头回转体作为水下航行体，其中圆柱体长L0，直径D0，距头部顶端0.56L0处为质心。在航行体表面总速度势中计入波浪入射势，以考虑波浪对水下运动航行体的影响，这样可简化自由液面处网格的划分，将实际物理模型(图1)简化为边界元计算模型(如图3(a)所示)。模型中，航行体发射水深为30 m，垂向速度为25 m/s，具有1.5 m/s的向弹体坐标系x轴负方向(艇速方向)的初始艇速。因为模型中不涉及出筒阶段，为考虑航行体水下发射实际情况，在数值模型中设置水下航行体初始的俯仰角速度为ω0，初始俯仰角为φ0。

(a) 航行体网格(a) Grid of the vehicle

如图3(a)所示，水下航行体结构表面用三角形网格进行划分，计算过程中将其视为刚体。模型中，设水下航行体在水中运动时为完全浸湿状态，忽略空泡等强非线性条件影响。

1.1 控制方程

在无旋、无黏假设下的理想势流理论中，航行体总速度势为：

Φ=φ+φi

(1)

式中，φ为结构表面的扰动势，φi为波浪入射势。

航行体总速度势满足拉普拉斯方程：

∇2Φ=0

(2)

结构表面满足不可穿透条件：

(3)

式中，n为物面法向向量，V为速度向量。

流场无穷远处满足：

∇Φ→∇φi

(4)

流场域内任意一点的速度势都可以用其边界上的速度势及其法向导数来确定[23]，所以需要采用边界积分方法[24]求解流场扰动势φ：

(5)

式中，S为航行体表面边界面，p和q分别为场点和源点。自由空间的格林函数G(p,q)=1/|R-r|，R和r分别是场点和源点的位置矢量。

将求解得出的速度势代入非定常的伯努利方程中，得到式(6)，将由式(5)求得的扰动势φ代入式(6)中求得水下航行体运动过程中所受压力，同时计及流场静压和大气压力。

(6)

式中：P0为大气压，水下航行体出水时其表面将只承受大气压力；h为距离水面的高度；ρ为海水密度。

水下航行体的结构动力学方程如式(7)所示：

(7)

式中，Ms为结构质量矩阵，Ks为刚度矩阵，fs为结构外力，Isf为联系结构单元与流体边界单元的转换矩阵，Af为单元面积矩阵。

将水下航行体表面新的单元、节点位置信息输入到流场动压力计算程序之中，计算在新时间步内结构表面各单元所受压力大小，然后更新节点、单元信息，循环计算到要求时间步长为止。

1.2 波浪入射势

本文计算工况中，波高相对于水深为小量，所以可以采用小振幅波理论对水下航行体在规则波浪中的运动进行分析。小振幅波模型如图4所示，图中，λ为波长，H为波高，A为波幅。

图4 小振幅波波面Fig.4 Small amplitude wave surface

小幅波面方程如式(8)所示：

η(x,t)=Acos(kx-ωt+ε)

(8)

式中，ω代表波浪频率，k为波数，ε为初相位。

小振幅波理论中，水质点运动缓慢，故自由表面非线性运动和动力边界条件可以简化为线性边界条件。因此，波浪向前传播时，波浪的入射势为：

(9)

若波浪的传播方向和坐标系之间存在夹角γ，则可以通过坐标转换得到新的波浪数学模型：

(10)

当艇速水平运动方向和波浪传播方向相同时为顺浪，此时γ=180°；当方向相反时为逆浪，此时γ=0°。

1.3 有效性验证

为验证算法的有效性，将在开放水池所测得的试验结果与数值模拟结果对比。试验工况为：初始艇速3.78ω0L0，垂直速度63.01ω0L0，波面状态为静水。

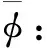
(11)

将计算所得的水下航行体头部触水俯仰角和尾部触水俯仰角，同试验结果进行对比，来验证算法的有效性。对比结果如表1所示，头部触水俯仰角和尾部触水俯仰角的相对误差较小，可以认为在姿态计算上算法有效。

表1 水下航行体出水俯仰角对比

为验证波浪力的有效性，采用海洋工程中常用的经验公式进行比较。对于与波长相比尺度较小的细长弹体(弹体D/λ<0.2)的波浪力计算，在工程设计中广泛采用莫里森公式[25]。该公式假定，柱体的存在对波浪运动无显著影响，认为波浪对柱体的作用主要是黏滞效应和附加质量效应。

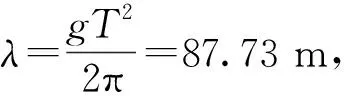
(12)

由于莫里森公式一般应用于静态或者准静态的结构物波浪力计算当中，所以本文在校核势流方法计算结果有效性时，假定柱体静止于水面附近，然后分别用莫里森公式和势流方法计算柱体单位长度所受波浪力大小，计算结果如表2所示。在水面处，应用势流方法比应用莫里森公式计算相比偏小，3级浪和5级浪误差分别为6.71%和9.56%，可认为计算结果符合波浪力有效性要求。结合上述对弹体出水俯仰角的验证结果，本文所建立的基于势流理论的航行体出水姿态计算模型符合有效性的要求，可以应用到本文的计算当中。

表2 莫里森公式和势流方法计算的单位长度波浪力对比

、

2 实时波浪预报方法

2.1 实际海况分析

实际海浪的波面运动是一种十分复杂的自然现象，受到自身重力、海面附近风速、风向、水面以下地形地貌特点，甚至是地球自转偏向力、潮汐作用等诸多复杂因素的影响，从而使其波动规律表现出极大的随机性，增加了对水面附近舰船和水下航行体的运动进行准确预测的困难程度。图5所示为渤海湾某一海域在台风下的30 min波面时历曲线,本文以该波浪作为实测海况进行水下航行体的出水姿态成功概率预报。

图5 波面30 min的时历曲线Fig.5 30-minute time-history curve of the wave surface

图6 实测波浪的波高统计直方图Fig.6 Statistical histogram of wave height of measured waves

为验证实测波高的分布规律，将实测波高进行累计概率统计，得到如图7所示的实测波高的概率分布曲线。同时为得到理论上的波高概率分布曲线，参考式(13)得到瑞利分布[25]下的波高概率分布，并将所得结果与实测波高概率分布进行对比，对比结果如图7所示，发现统计值和理论值的概率分布曲线拟合良好，认为波高的分布符合瑞利分布。

(13)

式中，f(H)为波高概率密度，P为对应的累计概率分布，Hmax为符合边界要求的最大波高。

图7 理论值和统计值对比Fig.7 Comparison of simulated values and statistical values

2.2 波浪参数对出水俯仰角的影响

波浪力可分为两部分[16, 22]：①由波浪压力场引起的压差力；②由于波浪质点的轨迹速度引起的附加惯性力。波浪参数通过影响波浪力的大小从而影响水下航行体的出水姿态参数。波高主要影响波浪力的幅值，对航行体出水姿态参数有着直接影响；波浪的周期T、初相位ε和浪向通过改变水下航行体出水相位来影响波浪质点的轨迹速度，改变附加惯性力，从而影响出水姿态参数。

将不同工况下的尾部触水俯仰角和静水下尾部触水俯仰角作差比得到俯仰角偏差值β：

(14)

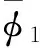
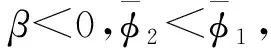
图8 不同波高下的俯仰角偏差值Fig.8 Deviation of pitch angle under different wave height

图9 不同出水相位下的俯仰角偏差值Fig.9 Deviation of pitch angle under different water-exit phase

通过图9可以发现，在该计算工况下，俯仰角偏差随着出水相位呈余弦变化规律，因为随着出水相位的变化，流体质点的轨迹速度是不同的，流体质点和波浪的传播存在相对运动，受到波浪相位的影响，流体质点运动速度的方向近似呈余弦变化。浪流的相对运动如图10所示，在波峰位置，波浪传播方向和流体质点的运动方向相同；在波谷位置，波浪传播方向和流体质点的运动方向相反。波峰位置和波谷位置浪流相对运动的不同，造成两个相位下航行体尾部触水俯仰角相反的情况：波峰位置出水，流体质点始终沿着x轴正方向运动[15]，此时弹体所受的附加惯性力偏向于航行体俯仰方向，波浪对尾部触水俯仰角的负影响达到最大；波谷位置出水，流体质点会沿x轴负方向运动[15]，此时弹体所受的附加惯性力对航行体俯仰运动呈抑制作用，波浪对尾部触水俯仰角的正影响达到最大。

图10 浪流相对运动Fig.10 Relative motion of waves and fluid particles

2.3 水下航行体出水成功概率预报

在潜艇实际海上作战中，海况是复杂多变的，在进行潜射导弹发射之前，需要对该海况下的发射成功概率进行快速预报。本小节针对此工程背景提出一种水下航行体出水成功概率的快速预报方法。

1)规则波浪数据的建立：为了提供基本的数据参考，将各个工况所算得的尾部触水俯仰角进行集成，形成规则波浪数据库。通过2.2节分析可知，相同波高下，俯仰角的变化受到出水相位的影响，在某一出水相位会出现最恶劣情况(即尾部触水俯仰角最小)。所以，在生成规则波浪数据库时，计算水下航行体在不同波高下最恶劣的工况即尾部触水时的最小俯仰角纳入数据库中。波高的计算范围参考北半球大洋海浪年平均统计资料，浪向取为逆浪，波高取变化范围[0,14]m，波高间隔0.5 m，每个工况计算所得的尾部触水俯仰角纳入规则波浪数据库中。通过图8可以发现随着波高的增加，俯仰角偏差值近似呈线性增加，所以，对于未曾计算到的波高(比如H=0.3 m)，可采用分段线性插值得到出水俯仰角。该数据库用于后续水下航行体出水成功的判定。

3)概率预报模型的建立：波高H的分布服从瑞利分布[25]，所以参考式(13)建立波高分布概率预报模型。

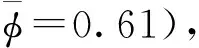
该实测海况下概率分布如图11所示，Hmax为满足要求的最大波高，0～Hmax为所满足的波浪范围，通过概率分布函数即可得到水下航行体的出水成功概率。水下航行体出水成功概率预报的流程如图12所示。

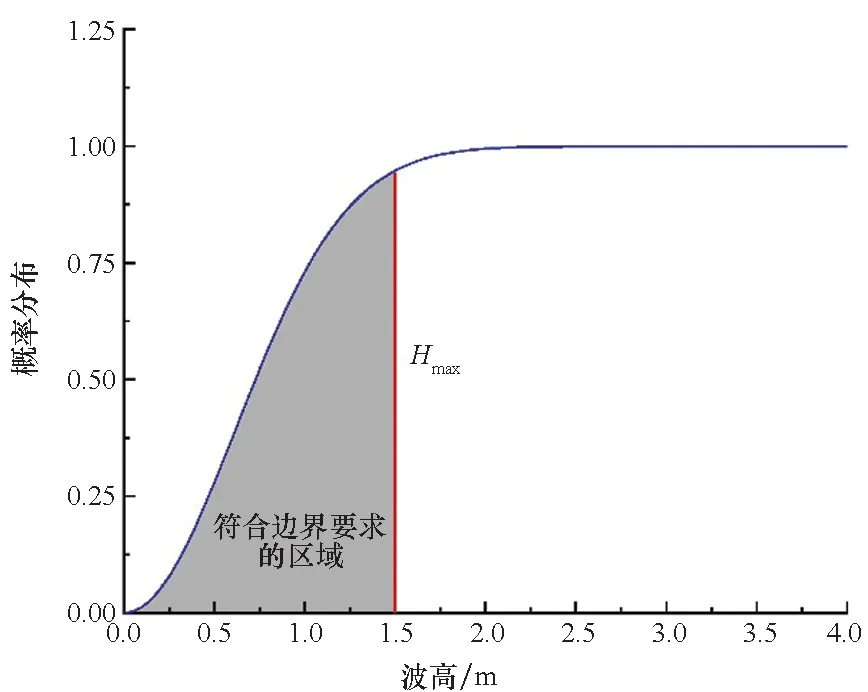
图11 波高的概率分布Fig.11 Probability distribution of wave height

图12 水下航行体出水成功概率预报流程Fig.12 Successful probability prediction process of underwater vehicles coming out of water

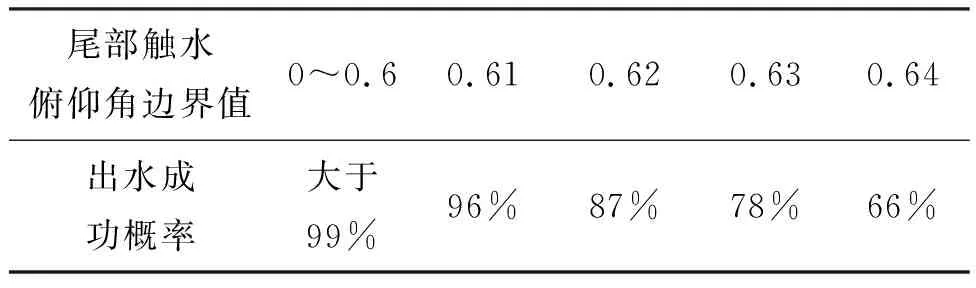
表3 水下航行体出水成功概率预报结果

3 结论

本文通过边界元计算方法实现了对水下航行体水下发射的数值模拟，对水下航行体在规则波浪下的出水姿态参数形成了规模计算，从而建立了规则波浪数据库。计算结果表明，在考虑最恶劣工况下，出水俯仰角偏差随着波高的增加而减小；相同波高下，出水俯仰角偏差随着出水相位呈余弦变化，俯仰角极值发生在波峰和波谷位置。

以尾部触水时的俯仰角作为水下航行体能否成功出水的判定，在认为波浪的波高符合瑞利分布的前提下，实现了在实测海浪下对水下航行体出水成功概率的预报。基于规则波浪数据库下的水下航行体出水成功概率预报方法具有如下特性：

1)快速性：该预报方法是从已经计算完成的数据库中抓取边界值，利用波浪分布的概率模型对出水成功概率进行计算，用时短暂，对于潜艇作战判定发射时机具有一定参考意义。

2)灵活性：该方法是参考北半球大洋海浪年平均统计资料进行工况划分，在实际应用时，可以参考不同海域的统计资料进行计算以形成数据库，进行预报的弹体模型也可以根据实际进行更换。

3)实用性：由于计算结果的线性变化，该方法只需要一定数量的原始数据，数据获取容易而且精度较高，具有一定的实用性。