找准思维切入点提升学生多角度解题能力——以一道中考题为例

肖新娥

(福建省南平市顺昌县第一中学，福建南平，353299)

在生活中，我们常常会将一种习惯性思维、固化性思维的人，称为“死脑筋”.其实，这些人主要是沉浸在固定的思维中，思维停留在原地，被自己设置的思维框架所僵化，不能展开想象、联想等，没有跳跃性思维和发散性思维，从而钻在牛角尖里不能自拔，由此可见，培养一个人的发散性思维多么重要.所以在数学学习中，我们要让学生学会数学的思考、进行数学的思维，这种能力可以使学生终身受益.发散思维又叫做求异思维、分散思维、辐射思维等.这种思维是对已知信息进行多方向、多角度的思考,不局限于既定的理解,从而提出新问题,探索新知识或者发现多种解答和结果的思维方式.其具有三大特征：变通性(思维灵活、随机应变)、流畅性(思维敏捷、反应迅速)和独特性(对问题能提出超乎寻常的、独特的、新颖的见解).

美国的心理学家吉尔福特认为：发散思维“是从给定的信息中产生信息，其着重点是从同一的来源中产生各种各样的为数众多的输出，可能会发出转换作用”，事实上发散思维就是将已知的信息从不同层面进行分析，从多个角度对问题加以比较探索，对知识的脉络纵横联系，顺向逆向比较，达到“信手拈来，呼之即出”的程度.这样的思维方式，能让学生对所学知识达到深度理解，对数学思想和数学方法进行建构感悟，增强了数学思维的开阔深刻和灵活创新，从而培养学生的思维品质，让大脑遇到问题能够灵活思考，从而事半而功倍.

那么如何培养学生养成发散性思维的习惯呢？在平时的学习过程中要学会多角度地思考问题，将所遇未知的难题转化为已知的，复杂的难题转化为简单的，抽象的难题转化为直观的，一般向特殊转化，正面向反面转化等，通过更多不同思维方式之间的相互转化，拓宽思维空间的广度与深度，从而寻求到解决问题的最优途径.发散性思维的习惯培养中，一题多解是通向这个终极目的地的一种方法.一题多解，可以使得学生从不同的角度和不同的方位，观察分析题目中的数量关系，根据题目的实际条件，首先确定思维的起点，继而沿着不同的思考方向寻踪觅迹，就能找到不同的解题方法.下面我们以一道中考题为例来展开探讨.

每年度的中考题中，试卷的最后一题一般称之为压轴题，这类题分数占比大，难度也比较大，主要是考验学生的综合应用知识和解决问题的能力，也是学生得分高低的关键之题.而压轴题中又尤以最后一问最难，但其难度也不是难不可及、高不可攀，我们要克服恐惧心理，层层剥茧丝丝入扣，因为压轴题都是由一些小题模块组合起来的，从每个小题模块条件入手，联系相关所学知识点，是可以找到解题思路的.

解题必须根据题目所给的信息，充分运用条件，明确目标，才能找到解题的方向.题目的条件和目标之间存在着一系列必然联系，这些联系是由条件通往目标的桥梁，用这些联系解题需根据联系所遵循的数学原理决定.有些题目的匹配关系有多种，这也是其可以一题多解的原因.解题时应在理解题意的基础上，找准条件与目标所遵循的数学原理，确定解题方案，寻找有效解题方法.

例(14分)(2014·南通)如图1，抛物线y=-x2+2x+3与x轴相交于A、B两点，与y轴交于C，顶点为D，抛物线的对称轴DF与BC相交于点E，与x轴相交于点F．

图1

(1) 求线段DE的长；

(2) 设过E的直线与抛物线相交于M(x1，y1)，N(x2，y2)，试判断当|x1-x2|的值最小时，直线MN与x轴的位置关系，并说明理由；

(3) 设P为x轴上的一点，∠DAO+∠DPO=∠α，当tan∠α=4时，求点P的坐标．

分析：本题(1)(2)两问考查了待定系数法求解析式，二次函数的交点、顶点坐标、对称轴；一元二次方程根与系数的关系.

(1) 根据抛物线的解析式即可求得与坐标轴的坐标及顶点坐标，进而求得直线BC的解析式，把对称轴代入直线BC的解析式即可求得；

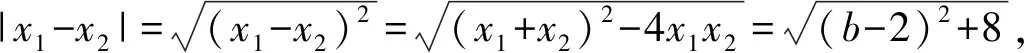
解：(1) 由抛物线y=-x2+2x+3可知，C(0，3)，

令y=0，则-x2+2x+3=0，解得：x1=-1，x2=3，

∴A(-1,0),B(3, 0)，

∴顶点x=1，y=4，即D(1，4)，

∴DF=4.

设直线BC的解析式为y=kx+b，代入B(3，0)，C(0，3)得：

∴解析式为：y=-x+3，

当x=1时，y=-1+3=2，

∴E(1, 2),

∴EF=2,

∴DE=DF-EF=4-2=2.

(2) 设直线MN的解析式为y=kx+b，

∵E(1,2)，

∴2=k+b,

∴k=2-b,

∴直线MN的解析式y=(2-b)x+b，

整理得：x2-bx+b-3=0，

∴x1+x2=b，x1x2=b-3，

∵b=2时，y=(2-b)x+b=2，

∴直线MN∥x轴.

当遇到压轴题中的问题时，我们首先要想到的是，解决几何问题时有一个“基本套路”：首先要认真分析条件，而分析条件就是将条件与相关“基本图形”结合起来，利用“基本图形”的性质，获得相应的结论.有时图形中不一定有与条件匹配的“基本图形”，那么就要去构造能与之取得联系的图形，方能找到解决问题的钥匙.

(3) 本题的切入点是添加辅助线，目的是构造相似三角形，解题策略是证三角形相似，通过相似比求线段长度.由最初的角的关系、正切值的关系到最后的求线段长度，可谓是质的飞跃，打开了解题思路，突破认识上的封闭.

解法一：

【信息读取】

∠DAO+∠DPO即∠DAP+∠DPO,考虑到△ADP中，三角形一个外角等于不相邻的两内角和，∠DAP+∠DPO=∠HDP=∠α, tan∠α= tan∠HDP=4.

【问题解决一】

∵∠AHP=∠AFD=90°，∠HAP=∠FAD，

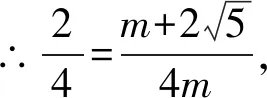
Rt△AHP中，由勾股定理得AP=20,OP=19,

则点P坐标为(19，0).

图2

解法二：

【信息读取】从正切值4入手寻求线索.

【问题解决二】

如图3，∵D(1，4)，

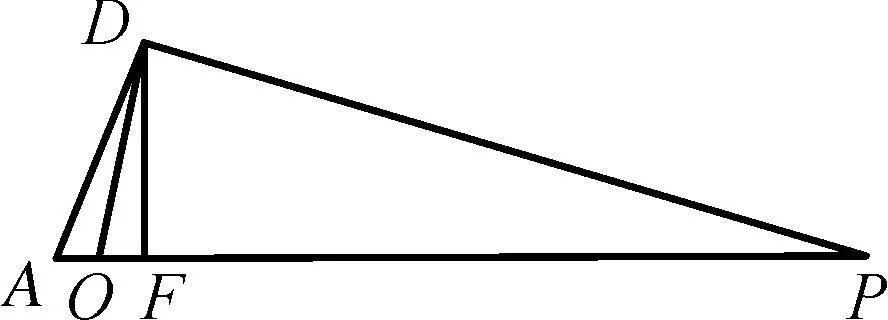
图3

∴tan∠DOF=4，

又∵tan∠α=4，

∴∠DOF=∠α，

∵∠DOF=∠DAO+∠ADO，

∵∠DAO+∠DPO=∠α，

∴∠DPO=∠ADO，

∴△ADP∽△AOD，

∴AD2=AO·AP，

Rt△AFD中AF=2，DF=4，由勾股定理得AD2=AF2+DF2=20，

又∵AO=1，

∴AP=20，即OP=19，

∴P(19，0)．

解法三：

【信息读取】

∠DAO+∠DPO=∠α， tan∠α=4，由题意可求得tan∠DAO=2，又tan∠α=4，那tan∠DPO等于多少呢？能否求tan∠DPO？如果tan∠DPO的值能求出，问题就变得简单多了.如果从这个问题考虑就要用到“两角和的正切公式”.

【问题解决三】

两角和的正切公式是高中阶段所学内容，这里介绍一下公式，∠A的正切记为tanA,∠B的正切记为 tanB,(∠A+∠B)的正切记为tan(A+B)，则它们之间有以下关系：

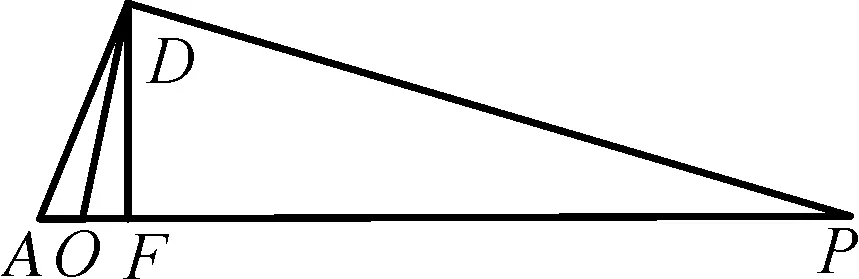
图4

中学生有时候往往凭直觉经验进行判断，他们会被事物的表象所迷惑，造成片面的、肤浅的感悟，不能从多方面分析问题，抓住事物的本质和解决问题的关键.中学生的年龄和心理特征使他们不能有目的、有条理地去思维，但同时他们的思维也没有桎梏，可以天马行空地想到老师所想不到的，发现老师所未能发现的.可见，中学生的数学思维虽具有不成熟性，但同时又具有可训练性，因此老师教学时要因势利导，才能让学生提高自己的思维层次，不固化思想，让思维得到发散与创新.

由于思考的角度和方向不同，让学生在解决问题的同时，又加强了对知识网点之间的多点衔接，多项数学基础知识在衔接中延伸扩充，多条数学规律在理解记忆中加深，多项解题技能在应用中生出技巧，久而久之的通过一段时间的他人培训，就能形成自我的训练和熟练.掌握一题多解的方法，还能从各种不同类型的题目中寻求出简单快捷的解法，这种思维方式和思考模型，能够有效地拓宽学生的解题思路，提高学生面对陌生和未知问题的分析能力.这种多角度思维切入点的抓取，需要我们老师在平时的教学过程中，通过联想、设想、类比、扩展，变化题目，让题目变身变形，从而得到一系列新的题目，甚至能得到具有一般代表性的结论，把学生从已知的此岸过渡到未知的彼岸.在如今“双减”的形势下，找准思维切入点，让学生多角度解题，能使得学生跳出题海，这不仅减轻了学生的课业负担，也减轻了老师的出题批改等一系列负担.