基于组合赋权和博弈论的TOD＋PPP项目风险研究

高 升 王齐荣 赵笑然 李 茂 钱海啸

(西南交通大学土木工程学院 四川成都 610031)

1 绪论

随着我国城镇化，城市建设如火如荼地发展推进，大城市盲目无序的扩张，城市人口逐渐流向郊区，市中心衰落，堵车严重，生态环境破坏、能源需求加剧、社区纽带断裂的问题日渐凸显，全然忘却为人服务的城市设计的初衷。基于如此局面，彼得·卡尔这位新城市运动发起者提出了最原始化的以公共交通为导向的联合土地开发模式[1](Transit-Oriented-Development，TOD)。在借鉴了大量实践应用案例，可以发现在同等建设量和开发力度下，TOD模式能最大限度地提高轨道交通的使用率，减少汽车出行量，缓解交通堵塞且可促进城市可持续发展[2]。

面对我国日益增长的轨道交通需求和投资资金匮乏的矛盾，合理的PPP模式应用与现有大热的TOD模式项目势在必行。根据柯永建研究[3]:由于参与者没有接受相关风险管理文化、管理人员经验不足、没有注重风险预防，使得风险管理往往发展“亡羊补牢”；历史项目经验借鉴不足，想当然地由管理者靠所谓经验进行判断，最后往往导致项目走向失败。基于此，利用改进层次分析法(AHP)的主观权重和改进熵值法的客观权重进行组合赋权得出各项风险的轻重缓急。最后通过博弈模型对双方进行合理的风险分配比例研究。

2 基于改进AHP-熵值法的组合赋权

2.1 改进AHP确定主观权重

层次分析法[4]，简称AHP，是一种权重决策分析方法。它将与决策有关的元素分解成目标、准则、方案等层次，结合了定性和定量分析来解决复杂的多目标问题，利用决策者的经验判断各衡量目标之间能否实现的标准之间的相对重要程度，并合理地给出每个决策方案的每个标准的权数，利用权数求出各方案的优劣次序。在构造判断矩阵时，多采用1～9标度法，该法存在矩阵一致性判断不协调和权重拟合时往往存在精确性不足的问题[5]。骆正清等[6]研究了权重拟合性、判断一致性等方面，建议使用指数标度e0/4-e8/4，提高精确性。具体步骤如下:

构建目标层、准则层、方案层，清晰看出问题中各内在因素之间的联系和构架。

(1)构造判断矩阵

采用指数标度e0/4-e8/4法[7]，对同层次因素指标进行比较赋值，通过两两因素相互比较并量化构成相应的判断矩阵A。

(2)计算权重及一致性判断

计算几何平均数:

归一化:

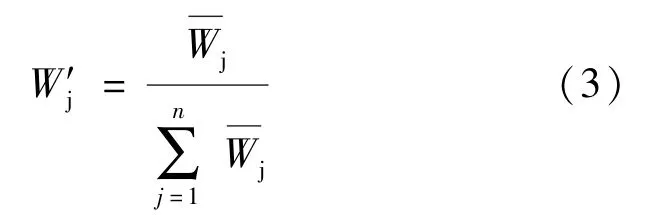
求最大特征值:

一致性判断:

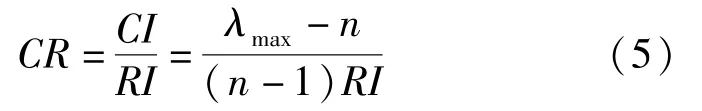
当CR＜0.1时，认为判断矩阵A通过一致性检验，否则需要重新构造判断矩阵。

2.2 改进熵权法确定客观权重

熵权法是一种根据变异性大小来确定权重的客观赋权法。不过在传统熵值法中，当指标权重ej→1时，ej之间的微小变化就会引起对应熵权的大幅度的变化[8]。本节对熵值法进行了改进。

原求权重的公式:

优化后求权重的公式:

用改进后公式计算求得权重为(0.249 2，0.249 7，0.250 2，0.250 7)，显然比较符合要求。当ej→0.5和ej→0时，经过计算得出改进的权重公式跟传统公式在非趋近1时并无大差异，结果如表1所示。

表1 权重计算

改进后熵值法具体计算步骤如下:

(1)指标无量纲标准化处理

(2)计算Pij，在第j个指标下第i个对象指标的权重

(3)计算信息熵

根据对数函数的基本原理，对数的数值不能为0，基于此种情况，一般情况下规定，当Pij＝0时，ln(pij) ＝0。

(4)通过修改后的公式(7)计算权重Wj

根据最小鉴别信息原理[9]，将主客观方法相结合，最终确定评价指标的综合权重。

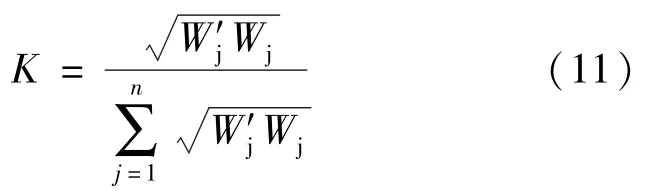
3 基于讨价还价形式的TOD项目中政府与合作方的博弈

为在TOD＋PPP项目中政府方与合作方均不想厌恶多风险分担，在他们之间并不能在短期内完全了解对方全部底细情况下，可采用讨价还价方式进行博弈[10]，从而得出最优合作方式。

3.1 博弈模型构建

第一回合由政府先出价，若合作方对价格满意，则谈判结束，否则进入第二回合。第二回合由合作方先出价，若政府满意价格，则谈判结束，否则进入第三回合，重复第一回合，直到双方达成共识。第一轮:政府方先出价，政府与合作方分担风险比例为k1∶(1-k1)，政府施压转移风险的概率p，转移的权重为x1，那么政府与其合作方分担比例分别为:

政府方的风险期望:

合作方的风险期望:

若第一回合中合作方拒绝政府方的出价，则进入第二回合的合作方先出价形式。政府与合作方分担风险比例为k2:(1-k2)，政府施压转移风险的概率p，转移的权重为x2，由于谈判需耗费双方的精力，引入政府和合作方的消耗系数分别为ζg、ζh，那么政府与其合作方分担比例分别为:

政府方的风险期望:

合作方的风险期望:

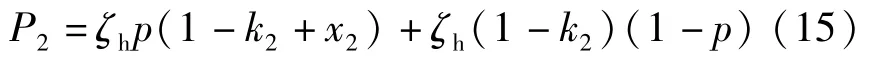
若第二回合中政府方不同意合作方的出价要求，则进入第二回合，由合作方先出要求。政府与合作方分担风险比例为k3:(1-k3)，政府施压转移风险的概率p，转移的权重为x3，由于谈判需耗费双方的精力，引入政府和合作方的消耗系数分别为，那么政府与其合作方分担比例分别为:

政府方的风险期望:

合作方的风险期望:

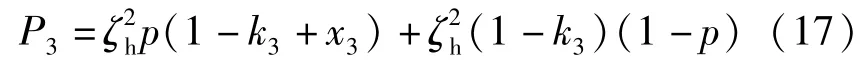
以此类推，直至双方达成满意合作方案。

3.2 模型求解

根据海萨尼转换理论[11]，在无限讨价还价的博弈过程中，无论逆推点设置在哪个回合都不会影响结果，为了研究方便，本节将第三回合设为逆推点。若G3≤G2，政府绝不会同意第二回合合作方的报价，但为了降低双方的谈判消耗，应满足G3≥G2。考虑到合作方的利益，最后的结果就是G3＝G2，即:

因为 0≤x3≤k3≤1，ζg≤ζp，0≤p≤1，所以P2＜P3，故第二回合双方都满意，谈判结束。

同理推理第一回合得出:

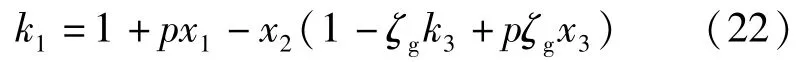
因为逆推点的选取不会影响结果，所以取k1＝k3，得:

由此得出，在政府方提出报价k时，由于双方地位的不协调，最终政府方提出风险分担比例为:

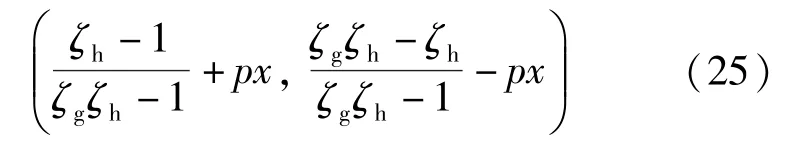
由于存在风险转移，实际风险分担比例:

同理，当合作方先提出报价时，合作方提出的风险分担比例为:

实际风险分担比例为:

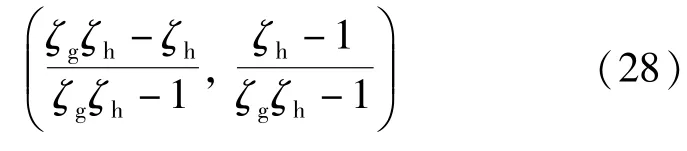
4 案例分析

4.1 项目简介

规划中的杭州市地铁一号线工程北起余杭区临平镇，沿沪杭高速公路，进入杭州市老城区，途经市区环城北路、延安路、解放路等主要干道，往南跨钱塘江，南端终于萧山区城厢，全线总长50.68 km，设有31个站点。项目采用政府与杭港公司合作投资的PPP模式。

4.2 工程实例分析

4.2.1 构建层次结构图

通过文献参考，采用4个二级指标，12个三级指标，构建了杭州地铁一号线风险评估层次结构图，如图1所示。

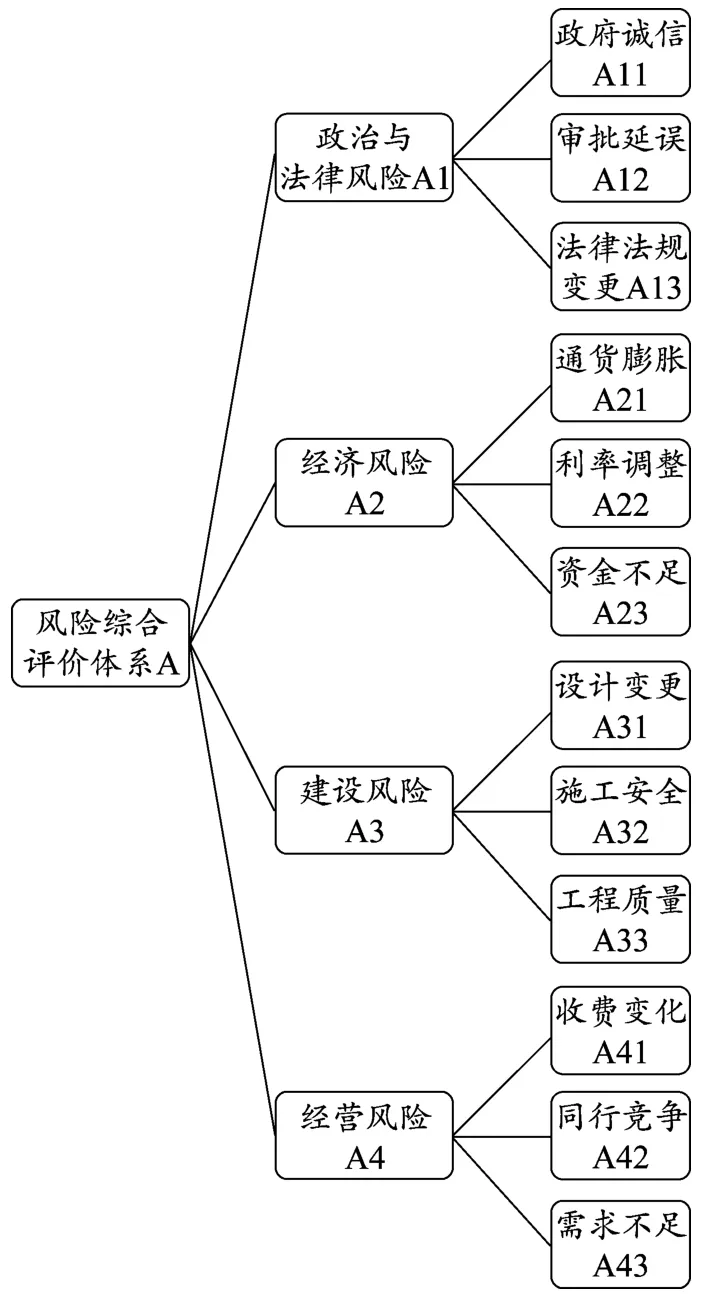
图1 层次结构图

4.2.2 组合赋权法确定权重

通过目标层对准则层风险因素两两比较得到判断矩阵A:

运用SPSS软件计算得出:

所以CR＝0.003＜0.1，通过了一次性检验。同理列出准则层对于方案层的各个判断矩阵，最终得到各评价指标的主观权重:

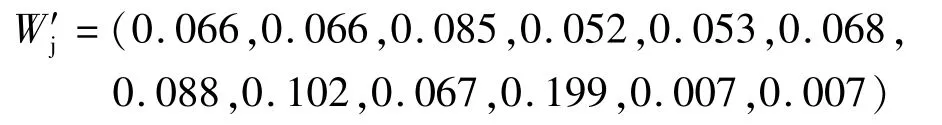
通过公式(6)～(9)得到各评价指标的客观权重:

根据公式(10)得出组合赋权下各指标的组合权重:

经过组合赋权法计算结果可知，政治和法律风险、建设风险占比较大。

4.2.3 博弈论下风险比例确定

通过在杭州地铁集团、港铁公司和政府相关官员进行问卷调查，得出杭州一号线风险分担初步方案，如表2所示。

由表2可得，其中政府方和合作方共担风险因素有7个，包括通货膨胀、利率调整、设计变更、施工安全、工程质量、同行竞争、需求不足。根据李妍[12]研究的博弈参数取值区间，其中:

再通过问卷数据量化得到杭州地铁一号线共担风险的相关参数取值，如表3所示。

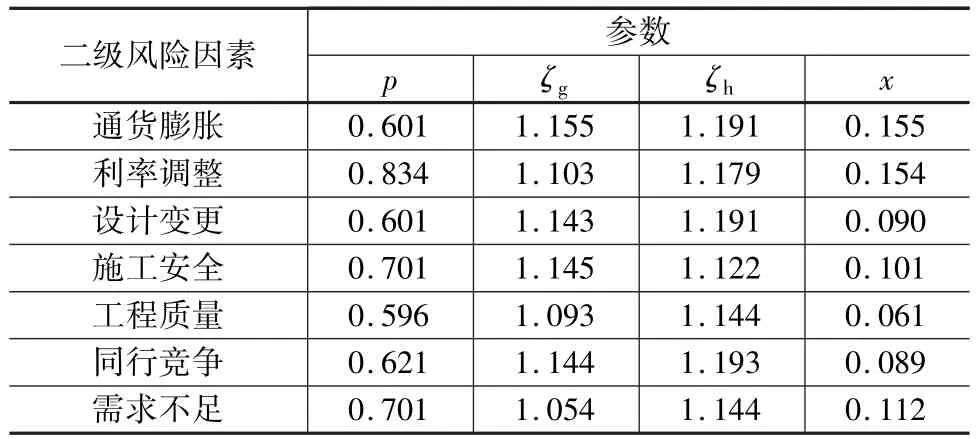
表3 杭州地铁一号线风险因素相关参数取值

由政府方先提出报价，根据式(25)、式(26)、式(27)、式(28)分别计算出二者的风险分担比例，结果如表4、表5所示。

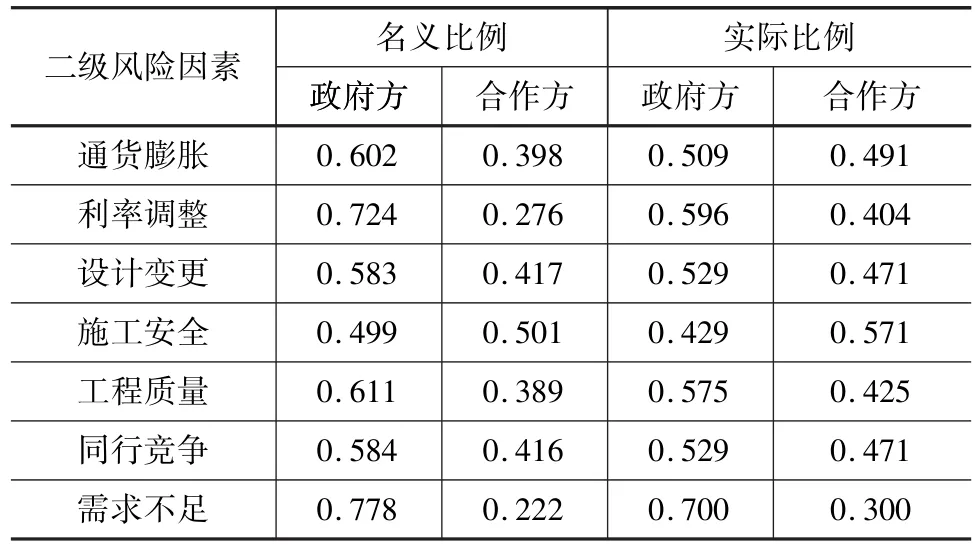
表4 政府方先出价下地铁项目风险分担比例

表5 合作方先出价下地铁项目风险分担比例

组合赋权法计算结果可知，在杭州地铁一号线全周期建设过程中，政治和法律风险、建设风险都是需要引起重大关注，这与柯永建对以往失败案例分析出的结果类同，风险分担比例结果也与现实合同文件相呼应。

5 结束语

本文基于改进AHP-熵权法组合赋权法对杭州地铁一号线艮山门地铁站TOD项目各风险权重占比研究，接着通过讨价还价博弈理论对风险进行分配，该模型在政府和合作方在短期内无法了解双方全部相关信息情况下，结合讨价还价方式，做出双方都彼此满意的合作方式。为现有的大热TOD模式下相关项目的合作方式谈判做出初步探索。本研究成果有利于科学分配风险比例、减少盲目PPP模式项目合作给双方带来极大损失，具有一定理论价值和现实指导意义。