温度效应对地铁桥梁数据预测模型影响研究
朱 力 朱尔玉 张 衡 白正伟 安小诗
(1.北京市地铁运营有限公司地铁运营技术研发中心 北京 100089;2.北京交通大学 北京 100044)
1 引言
近些年国内外学者对桥梁工程健康检测系统的研究逐渐增多,这也与我国桥梁工程发展阶段有直接的关系[1]。影响健康监测系统数据预测精度的因素中温度效应是主要的影响因素之一。
李全林[2]通过对日照下混凝土箱梁温度场和温度应力的研究,深入分析了温度效应在桥梁健康监测系统中对数据预测的具体表现。在对桥梁结构监测数据的预测模型建立方面,Kaveh[3]、黄方林[4]等人均从不同的技术方面对桥梁健康监测系统展开了一系列研究。刘夏平等[5]研究了桥梁挠度监测中温度效应的分离,严鹏[6]开展了桥梁检测信号中的降噪工作。在对桥梁检测系统中温度效应的具体影响研究方面还有待更为深入地分析研究。
本文通过使用改良的数据预处理方法,实现了对地铁桥梁高频监测数据的预处理,克服了传统方法对高频数据剔除过度的问题;采用对监测数据和温度效应的回归分析,建立不同测项与温度和温差的回归方程,使得温度效应从监测数据中得到了分离;通过对基于温度效应的ARMA预测模型和单因素ARMA预测模型的预测结果进行对比,得出了温度效应对数据预测模型的影响是不可忽略的结论。
2 数据分析方法
2.1 数据预处理
2.1.1 传统的3σ法的弊端
主要对以下方面进行对比:
(1)低频数据最大值与最小值的差;
(2)传统3σ法异常数据识别区间的长度;
(3)高频数据最大值与最小值的差。
通过对比发现使用3σ准则计算得到的剔除区间是不符合动态数据实际变化规律的,会对列车经过时的数据造成错误剔除。
2.1.2 改良的3σ法方案的提出
在综合比较了各个测点高低频数据的变化范围之后,本文对传统3σ准则中方差σ2的计算方法进行了改进,将统计得到的方差σ2放大,来弥补监测数据中动态数据过少的问题。经过试算发现,当统计得到的方差σ2扩大4倍,即标准差σ扩大2倍时,异常值的识别区间可以较大程度地将列车经过时的峰值数据包含在内,不会将正常数据识别为异常值。根据动态数据修正的标准差为σD=2σ,则基于动态数据的异常值识别区间范围变为,当数据落于[ω2,ω1]区间之外时,数据被识别为异常值并剔除。
注1 一、二阶异构多智能体系统一般包含多个一阶系统和多个二阶系统,而本文中系统式 (1) 与此略有差异,因此也可称系统式 (1) 为“伪异构系统”,即异构系统的特殊化处理.
2.1.3 异常值插补方法的研究
由于地铁桥梁健康监测数据有着变化趋势明显、数据量大且很少出现连续缺失值的特点,提出了改良的最近邻插补法[8]。根据距离的权重使用缺失值附近k个有效值对缺失值拟合,权重根据距离反比分配,距离越近的数据权重越高,随着距离增加权重降低。选择缺失值的前n个值对其进行插补,则插补值的计算公式为:

式中,yi为缺失值附近的有效值;Di为有效值到缺失值的距离;Y为插补值。
本文统一选用缺失值的前4个数据对缺失值插补,则具体的计算公式为:

2.2 温度效应与监测数据回归分析
以2016年1月份到12月份北京地铁某线连续梁桥的梁体纵向位移为例进行分析,其监测数据如图1所示,期间监测的温度值如图2所示。通过对梁体位移数据和温度数据图像的对比可以看出梁体位移与温度的变化趋势十分相似。以温度为横坐标,梁体位移为纵坐标绘制图形,可以初步判断位移与温度之间是存在线性关系的。为将温度效应从监测项中分离,使用线性回归模型[9]来确定温度与监测项之间的关系。

图1 北京地铁某线119~120墩段梁体纵向位移
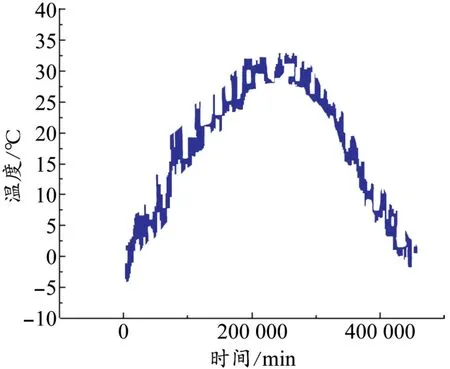
图2 北京市2016年1月份到4月份温度检测值
假设监测项与温度和温差之间的线性回归模型为:

式中,YT为温度效应回归的值;XT为监测的温度数据;XΔT为温差数据;a1为温度项的系数;a2为温差项的系数;b为常数项。当测项只与温度存在回归关系时,系数a2=0;当测项只与温差存在回归关系时,系数a1=0。
选用0:00~5:00之间地铁停止运行的时间段的监测数据做回归分析,其与温度效应的回归结果更准确。使用Matlab软件来对温度、温差与监测项之间的回归方程进行计算,部分统计结果如表1所示。

表1 不同测项与温度和温差的回归方程
2.3 监测数据中分离温度效应的研究
梁体位移、应变等数据主要受温度变化、风荷载与列车荷载的影响,本文研究的桥梁均为中小跨径桥梁,未考虑风荷载对桥梁位移、应变等其他测项的影响,则监测数据的变化主要受温度变化与列车荷载的影响,如式(4)所示:

式中,Y为梁体位移、应变等监测值;YT为温度引起的变化量;YV为列车荷载引起的变化量。
以梁体纵向位移为例,对数据的温度效应进行分离。由于其对温度的回归方程为:
YT=-12.02+0.535XT
原始监测数据中减去温度代入回归公式即可将数据中温度影响去除,即Y-YT。
原数据由于温度效应的存在,自身是存在趋势性的,而且分离出温度效应之后的数据,位移的变化更趋于随机,相反趋势性明显减弱。
使用自相关系数来评价分离温度效应后数据的平稳性,在做差之后,数据的前五百阶自相关系数由做差前的0.98左右减小到0值附近,说明数据平稳性显著增加。
其做差前后的前五百阶自相关系数分别见图3和图4。将分离温度效应后的数据再与温度计算相关系数,得到的值在0.01以下。结合趋势性与平稳性分析,此种分离温度效应的方法可以使得处理后的数据不再与温度相关。

图3 梁体纵向位移去除温度效应前的自相关系数

图4 梁体纵向位移去除温度效应后的自相关系数
3 预测模型的建立
基于温度效应的预测模型将数据整体的趋势变化分为了两部分考虑,整体均值的变化趋势由温度效应来体现,而数据波动性则使用时间序列来对其建立数学模型来体现,将两部分预测数据相结合即为最终的预测数据。从温度和时间两个方面对监测数据进行预测的模型,即为基于温度效应的时间序列预测模型[10]。
4 预测结果对比分析
4.1 基于温度效应的ARMA预测模型
在将预测数据与原始数据比对之前,需要将预测数据进行逆向标准化、逆向差分、回填温度效应三步处理[11]。回填温度效应是给经过两部处理后的预测数据加上温度效应项。对原始数据的前4 195个数据进行预测,预测样本与原始数据进行对比,观察预测样本的拟合效果,其对比图见图5。
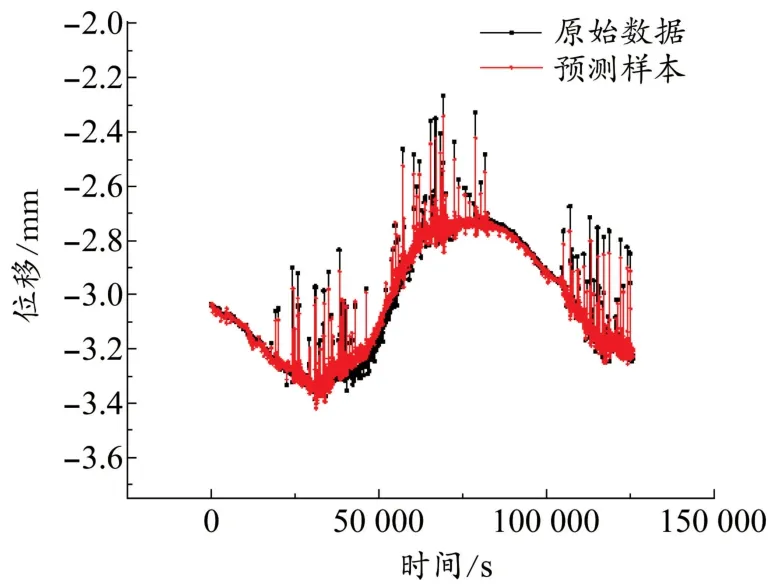
图5 训练样本与原始数据对比
将2016年1月2日中午12时的实测温度代入到温度效应,回填到ARMA模型预测的中午12时的预测数据当中,再与中午12时梁体纵向位移的实测数据进行比较,观察预测数据的拟合效果。预测数据与实测数据的对比图如图6所示。梁体纵向位移的预测值与实测值相比较,预测值的变化趋势与数值所在范围与实测数据的大致类似,可以认为预测值能够反映实际数据的变化规律。表2列出了120个数据中的前15个预测数据与实测值之间的相对误差。
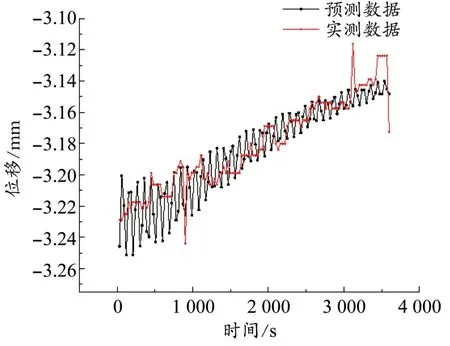
图6 未来1 h预测数据与实测数据对比

表2 预测数据与实测值之间的相对误差
4.2 ARMA预测模型结果分析
数据预处理过程与前文相同,但不进行分离温度效应这一步骤。预测数据与实测数据对比如图7所示。由于对未来数据进行的是无样本预测,预测数据无法准确地给出数据的变化趋势。随着预测时长的增加,预测数据与实测数据之间偏差越来越大。同样使用相对误差来评判不考虑温度效应的时间序列模型的预测效果。不考虑温度效应的时间序列模型前15个预测数据与实测值之间的相对误差如表3所示。可知预测数据的前十几个数据的相对误差不太大,但是120个预测数据的相对误差的绝对值的平均值为1.78%,最大相对误差为3.96%,两项指标均为基于温度效应预测模型误差的数倍。只考虑温度效应,使用温度的回归模型作为单因素预测模型对数据进行预测。

图7 时间回归模型预测数据与实测数据对比
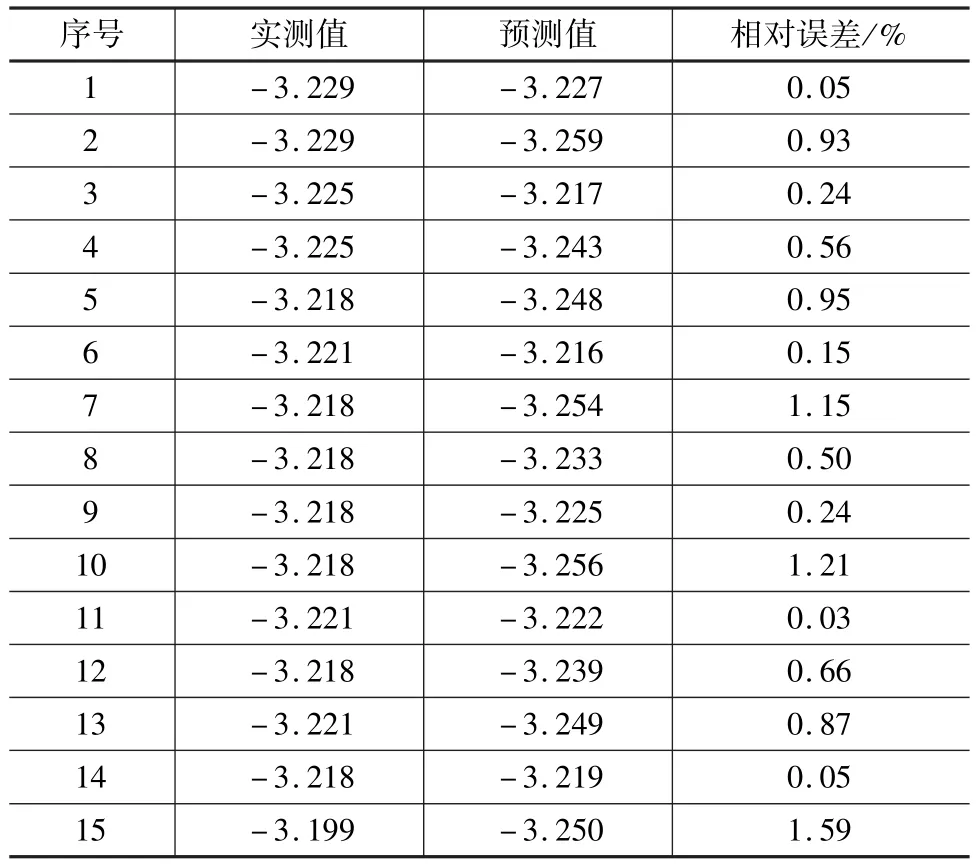
表3 时间回归模型预测数据与实测值相对误差
由于简支梁桥的梁体纵向位移与温差不存在回归关系,其与温度的回归方程为:

将2016年1月2日中午12时的温度代入到温度回归方程中,温度预测模型的预测数据与实测数据对比如图8所示。前15个预测数据与实测值之间的相对误差如表4所示。

图8 温度回归模型预测数据与实测数据对比
由表4可知预测数据相对误差较大,120个预测数据的平均误差为12.80%,最大相对误差为15.27%。

表4 温度回归模型预测数据与实测值相对误差
基于温度效应的时间序列预测模型的准确度是相当高的。计算120个数据的相对误差的绝对值平均值为0.50%,其中最大相对误差为1.04%;仅考虑单因素的时间序列模型误差的绝对值平均值为0.61%,其中最大相对误差为1.59%;而仅考虑温度效应的预测模型误差的绝对值平均值达到了11.46%,其中最大相对误差为11.96%。
5 结束语
(1)通过对传统的数据预处理方法进行改进,解决了传统数据预处理方法无法准确处理桥梁高频监测数据的问题,并通过将方差放大得到可应用于桥梁高频监测数据处理的改良版3σ法和异常值插补法。
(2)通过温度效应对桥梁监测数据的影响分析,建立了基于温度效应的不同测项与温度和温差的回归方程,建立了一种高效的分离温度效应的机制。
(3)通过ARMA时间序列模型对数据进行预测,并将预测结果与基于温度效应的ARMA时间序列模型预测得到的预测结果进行了比较,得出了基于温度效应的ARMA时间序列模型预测效果更好的结论,并证明了温度效应对预测模型建立不可忽视的影响。

