基于MPC的车车通信时间同步方法

陈 永，詹芝贤，张 薇

（1.兰州交通大学 电子与信息工程学院，甘肃 兰州 730070；2.兰州交通大学 交通运输学院，甘肃 兰州 730070）

列车运行控制系统作为高速铁路的中枢神经，是保障高速铁路运营安全、提高运营效率的核心技术装备。目前，我国CTCS-3列控系统使用车地通信系统进行列控信息双向传输［1］，但随着高速铁路的快速发展，对运营效率和安全防护提出了更高的要求。

随着5G“新基建”战略的部署和推进，铁路专用移动通信系统（The Fifth Generation Mobile Communication-Railway，5G-R）作为我国铁路未来移动通信的主体技术制式，可为列控系统提供大带宽、高可靠性的无线接入保证［2］。列车与列车之间的通信（车车通信）作为5G-R 重要应用场景，可进一步提升列控业务的安全性和运营效率。然而，在5G-R 车车通信过程中，由于列车的高速移动性，车车通信链路具有较大的时变性［3］，导致同步性能下降。如何提高车车通信时间同步性能，对于保障高速铁路运营安全及运营效率至关重要。

根据车车通信有中继和无中继不同场景［4］，目前对于实现时间同步的方法可以分为：集中式时间同步方法和分步式时间同步方法［5］。其中集中式时间同步方法一般需要设置参考节点，为同步过程提供参考时间。Shi 等［6］提出了1 种快速泛洪多路单向广播时间同步协议，它通过将参考时间沿多跳路径泛洪到整个网络上实现时间同步，但该方法一旦单个节点发生数据包丢失就会影响到整个网络的同步精度。Wang等［7］在时间同步过程中引入了比例积分微分（Proportional Integral Derivative，PID）控制降低干扰带来的误差，但无法适应快速时变带来的时钟跳变。Son 等［8］基于精准时间同步协议（Precision Time Protocol，PTP）提出了一种时钟同步方法，通过收集和分析其他节点的时钟信息来估计出故障节点的信息，但该方法未考虑数据包丢失的因素，存在估计不准确的问题。Shivaraman 等［9］提出了1 种基于集群的时间同步协议，但该方法无法降低由数据包丢失带来的同步误差。Jia 等［10］提出了1 种基于聚类算法的时钟同步协议，但该方法未考虑数据包丢失对同步过程带来的影响。

对于分布式时间同步方法，由于缺少中继参考时间，一般采用平均时间一致性（Average Time Synchronization，ATS）理论实现通信双方时间的同步［11］。Wang等［12］使用ATS 时间同步方法，对使用加权中值得到时钟偏移估计值后进行补偿。Shi 等［13］提出了1 种多跳平均一致性时间同步方法，通过虚拟链接增强网络代数连通性，提高收敛速度。Phan等［14］提出了1种基于ATS的虚拟拓扑时间同步方法来加快收敛速度。但上述分布式时间同步方法相比于集中式同步方法，普遍存在收敛速度慢的缺点［5］，无法适应5G-R 无线信道的快速时变性。综上所述，现有车车通信时间同步方法大部分研究未考虑报文丢失对同步的影响，导致存在同步精度低、算法收敛速度慢等问题。

本文提出了1 种基于模型预测控制（Model Predictive Control，MPC）的5G-R 下车车通信时间同步方法。建立了5G-R 下车车通信同步时钟模型，并引入观测器方程，构建了基于MPC 的前后车时钟状态空间模型和增量式预测模型，通过多步预测、滚动优化和负反馈调节等控制方式，完成不同场景下车车通信时间同步。

1 5G-R车车通信时间同步分析

5G 标准中的临近服务技术可支持车车通信技术［15］。车车通信技术分为2 种场景：一种是直接通信无中继模式；另一种是通过中继站进行间接通信有中继模式，相邻列车间通过下一代基站（Next Generation NodeB，gNB）间接完成前后车的信息交互，如图1所示。

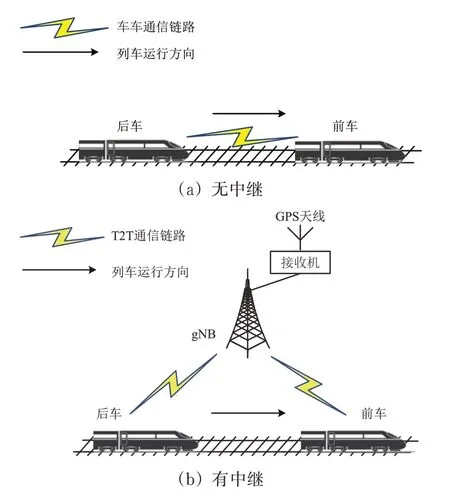
图1 5G-R下车车通信场景示意图

相邻列车之间的高精度时间同步，是实现车车通信的关键。在5G-R 下车车通信时间同步要求其时间精度优于±50 ms［16］。时间同步精度越高，相邻前后车获取列车速度和位置等重要控制信息的实时性就会越高，更有利于提高列车的运行安全。为了满足车车通信链路高精度的要求，相邻前后车的时间同步需要使用PTP 协议完成。PTP 协议同步精度可达亚微秒级，它可为设备提供高精度的时间服务，用以支持车车通信等业务的高精度时间同步要求以及同步测量等要求［16-17］。PTP 协议作为一种双向信息交换机制的时间同步协议，主从时钟通过相互交换携带时钟戳信息的PTP 报文完成时间同步，过程如图2 所示。图中：i 为相邻的前后车时钟节点，i ∈{1，2}；T1，T2，T3和T4分别为PTP 报文在参考时钟与前后车时钟之间传输时的时间戳信息；θ 为参考时钟与前后车时钟之间的时间偏差；d 为参考时钟与前后车时钟之间的路径延迟。

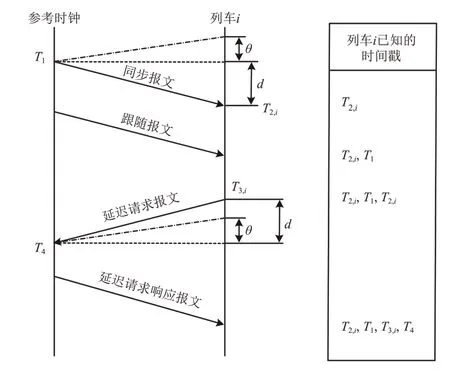
图2 5G-R车车通信时间同步过程

通常，假设PTP 协议报文在主从时钟之间的传输路径是对称的，则前后车与参考时钟之间的时钟偏差θi为

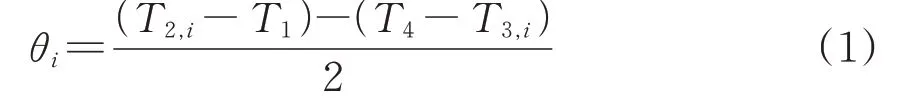
前后车与参考时钟之间的路径延迟di为

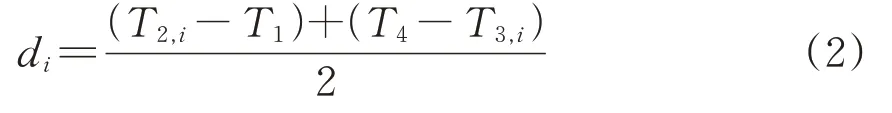
根据式（1）和式（2），可以计算得到前后车与参考时钟之间的偏差时间，从而实现与参考时钟之间的时间同步。

在5G-R 下车车通信过程中，无论是有中继场景还是无中继场景，实现车车通信时间同步的目标为对于标准参考时钟L（t），通过对前后车本地时钟Si（t）进行动态调整，最终与标准参考时钟L（t）保持一致，从而实现前后车的时间同步。车车通信时间同步过程参考时间S（t）的设定，则需要根据不同的车车通信场景进行设置。

（1） 当车车通信处于有中继场景，中继站gNB 通过内置GPS 接收机，获取标准时间信号，因此可将gNB 设定为参考时钟。此时，若前后车本地时间Si（t）与参考时间之间的最大误差e（t）满足

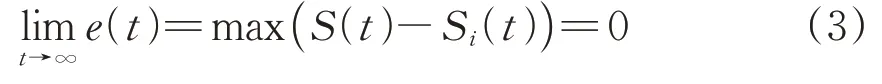
满足式（3），则完成有中继下车车通信时间同步过程。

（2）当车车通信处于无中继场景，由于该场景缺少提供标准时间的物理参考时钟，需要设定1个虚拟参考时钟，此时可以将相邻车视为独立自主的智能体，通过时间信息交互，动态设置虚拟参考时钟的时间。将前后车本地时间Si（t）与虚拟参考时间保持一致，从而实现前后车同步，即

式中：c（t）为虚拟参考时间。

2 车车通信同步时钟模型建立

2.1 理想时钟模型

在车车通信时间同步过程中，首先要建立车车通信同步时钟模型。车车通信时间同步的过程中，相邻的前后车和中继站gNB 都配备了本地时钟模块，中继站gNB 的时钟模块由于内置高精度压控晶振，其本地时间能够保持稳定［18］。而前后车时钟模块由于内置普通晶振，受其物理特性影响易受温度和压力等外界环境因素影响，晶振会出现不同程度的随机抖动，从而发生一定的时钟频率和相位偏移。前后车不同时钟与参考时钟之间的时钟相位偏移θi（t）可定义为

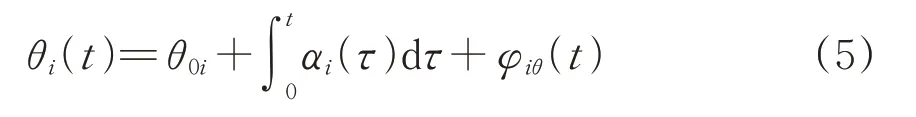
式中：θ0i为节点i的初始时钟相位偏移；αi(τ)为节点i在τ时刻的时钟频率偏移；φiθ(t)为节点i在t时刻受环境变化影响带来的随机时钟相位抖动。

同理，前后车不同的时钟与参考时钟t 之间的时钟频率偏移αi（t）可定义为

式中：α0i为节点i 的初始时频率偏移；φiα(t)为节点i在t时刻的随机时钟频率抖动。

在MPC 车车通信时钟同步求解时，由于MPC的求解方法基于被控对象的离散空间状态方程，因此需要将式（5）和式（6）的连续微分方程进行离散化处理，得

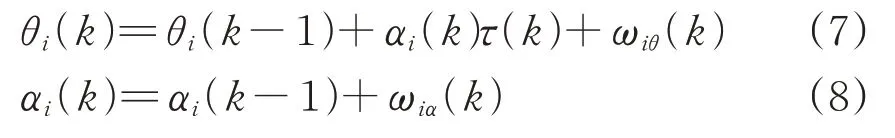
式中：k 为时间同步周期次数，k=1，2，…；ωiθ(k)为第k 次时间同步周期的时钟相位抖动，其服从零均值方差为的正态分布；ωiα(k)为第k 次时间同步周期的频率抖动，其服从零均值方差为σ2α的正态分布。

2.2 实际时钟模型

在建立完车车通信理想时钟模型后，需要进一步对车车通信实际时钟模型进行建模。

在实际5G-R 下车车通信时间同步过程中，受5G-R 无线信道快速时变性的影响，PTP 报文在车车通信链路上传输时会出现链路非对称、传输时延随机抖动以及数据包丢失等问题［19］。上述问题会造成PTP 时间戳不确定性误差，将严重影响PTP协议在车车通信链路上的时间精度。一般情况下，将不确定性时间戳误差假设为服从高斯分布的随机噪声，从而得到前后车实际时钟相位偏移模型θiM为

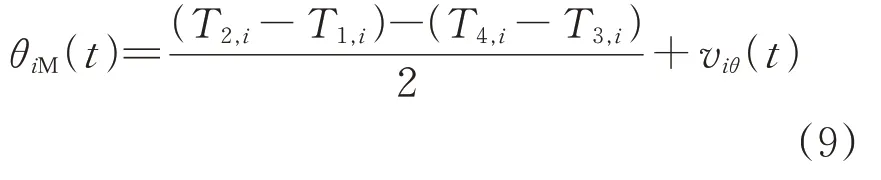
式中：viθ为时钟相位偏移随机噪声，其值服从均值为0、方差为的正态分布。

3 5G-R车车通信时间同步方法

在完成车车通信时钟同步模型表示后，本文提出了1种基于模型预测控制MPC的5G-R下车车通信时间同步方法，以提高车车通信同步性能及效率。MPC 是1 种基于模型的闭环优化控制方法，具有快速瞬态响应、高控制带宽等特性，适合应用于快速时变场景［20］。

在本文方法中，首先根据车车通信不同场景，设置前后车时间同步跟踪的参考时钟。然后，将前后车的时钟状态作为MPC 控制器的输入，分别构建前车与后车的MPC控制器，并通过对MPC输入量预测输出、迭代滚动优化和反馈校正，实现前后车与参考时钟的一致性跟踪，进而完成车与车之间的时间同步，本文方法MPC 控制器建立过程如图3 所示。图中：r（k）为MPC 控制器的参考时钟选择，其值根据不同的车车通信场景选择，当有中继场景时，将中继站gNB 的时钟作为参考时钟，当无中继场景下，通过前后车时间信息交互，动态设置参考时钟时间；ui（k）为控制输入量；yi（k）为前后车时钟状态输出值；(k)为当前列车时钟状态的预测输出值；k+n|k)为未来n 个同步周期内的列车时钟状态输出值。

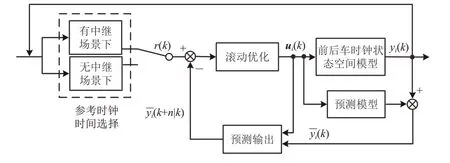
图3 前后车MPC控制器建立过程示意图

在通信场景参考时钟选择后，通过分别建立前后车MPC 控制器完成车车之间时间同步，其具体步骤如下。

步骤1：根据车车通信同步时钟模型，建立面向模型预测MPC 的车车通信时钟状态空间模型，得到相应的前后车时钟状态输出yi（k）。

步骤2：根据当前列车的时钟状态，构建预测模型，得到当前列车时钟状态的预测输出值

步骤4：以最小化预测输出yˉ和实际输出y 之间的偏差为目标，设计二次型矩阵形式的代价函数J，利用二次规划求最优方法进行滚动时域求解，得到下一同步周期前后车不同的输入控制量ui的优化解。最后，使用最优控制输入量ui进行反馈校正，迭代上述步骤，不断通过修正ui最终实现前后车对参考时钟的跟踪，从而完成车车时间同步。

3.1 状态空间模型

根据MPC 车车通信同步步骤，首先需要建立车车通信的状态空间模型。MPC 作为一种基于状态空间模型的最优控制方法［21］，其通过状态空间模型来预测前后车时钟在未来时刻的状态和输出，状态空间模型的具体过程如图4所示。

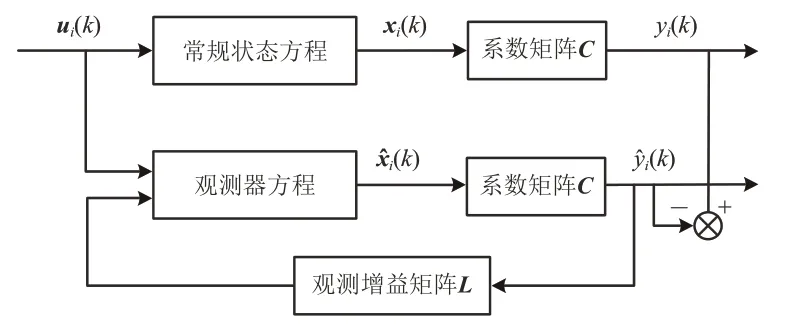
图4 时钟状态空间模型过程示意图

从图4 可以看出：本文车车通信同步状态空间模型由常规状态方程和观测器方程构成。在某一同步周期k时，若未发生PTP报文丢失，即前后车的时钟状态可通过PTP 报文传输被准确量测时，这时使用常规状态方程计算得到前后车在第k 次周期的准确时钟状态xi（k），然后通过维度系数矩阵C得到时钟状态输出标准参考时钟yi（k）；若发生PTP报文丢失时，此时前后车时钟状态无法被准确量测，需要引入观测器方程，通过观测增益矩阵L对观测器方程得到的输出估计值），并进行负反馈调节，使得观测器得到的前后车时钟状态输出估计值k）无限接近于标准参考yi（k）值，从而完成车车同步过程。

对于图4 中观测方程的建立，在有中继场景下，可结合式（7）—式（9），并加入控制输入量u，通过不断调整u来使前后车与gNB参考时间保持一致。而在无中继场景下，由于缺少准确的物理参考时钟，式（4）中的虚拟参考时钟时间c（t），需要根据前后车时间动态调整而实现车车同步。因此，针对车车通信2 种场景的特点，建立不同场景下车车通信时间同步过程的MPC状态空间模型为

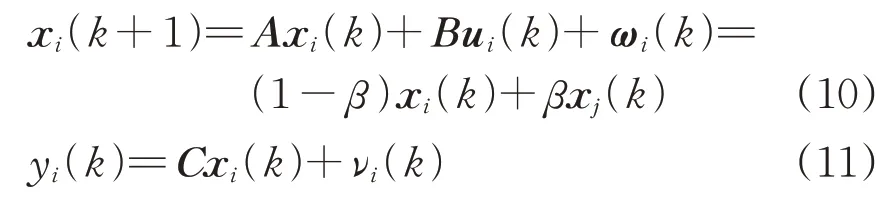
其中，

式中：xi，ui和yi分别为列车时钟节点i的状态、控制输入和输出；A，B 和C 为适当维数的矩阵，由系统决定；ωi和νi分别为由5G-R 无线信道不确定性带来的系统输入扰动和输出扰动；β 为动态系数；xj(k)为当前时刻列车时钟节点j的时钟状态。

在实际车车通信过程中，由于5G-R 无线信道环境复杂多变，PTP 协议传输时钟信息时不可避免地会出现丢失的情况，使得前后车时钟状态测量值在规定的同步周期内无法准时到达，造成前后车无法做到精确时间同步。为了降低由于数据包丢失导致的时钟状态不可量测带来的误差，引入观测器对不可量测的时钟状态进行准确估计，观测器具体的观测方程为

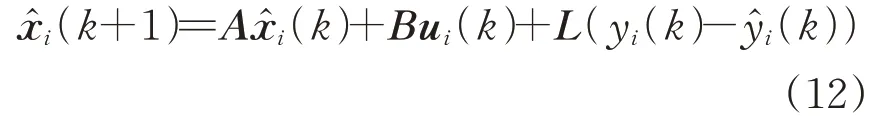
为求解观测器增益矩阵L，引入真实状态和观测器估计状态的误差向量e，其计算式为

代入式（10）和式（12），对式（13）进行展开化简，得到

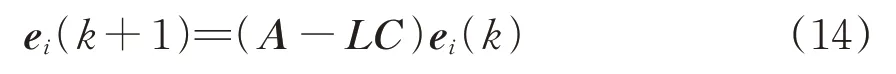
由于A和C是由系统决定的定值，一般使用极点配置法，通过保证矩阵A-LC 的所有特征值均在单位圆内，计算出L值。

由式（14）可知：矩阵A-LC 的极点值决定了观测器的估计误差e 能否最终收敛到0。当得到在数据包丢失时的状态观测器估计值之后，为了进一步描述因5G-R 无线信道导致的数据包丢失现象，引入服从伯努利分布的随机变量γ［k］描述第k次同步周期的PTP 报文的丢失，当以1－p 的概率γ［k］取1时，代表该周期报文未丢失，则当前时刻时钟状态可量测，使用式（10）进行计算；若以p 的概率γ［k］取0 时，代表发生报文丢失、时钟状态在第k次周期不可被量测，则使用式（12）得到的时钟状态估计值代替无法被量测的空状态值进行计算。

结合式（10）—式（12），最终考虑数据包丢失的前后车状态空间模型为

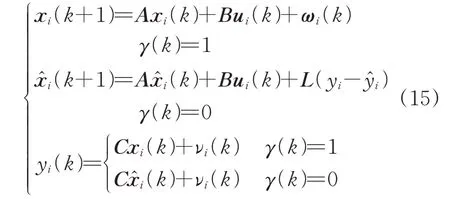
3.2 预测模型

在完成车车通信状态空间模型的建立后，建立车车通信时钟状态预测模型。在预测模型建立时，为了消除外界环境带来的时钟不确定输入扰动和由5G-R 无线信道带来的不确定输出扰动对预测输出结果的影响，使用增量式状态空间预测模型代替传统预测模型。

设5G-R 无线信道短时扰动不变，将式（15）重写为增量形式，得到

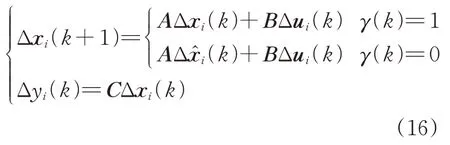
在状态增量式（16）的基础上，引入额外状态变量输出y 对原模型进行扩展，得到增量式状态向量为

联立式（10）、式（16）和式（17），得到输出增量式的扩展模型即预测模型为

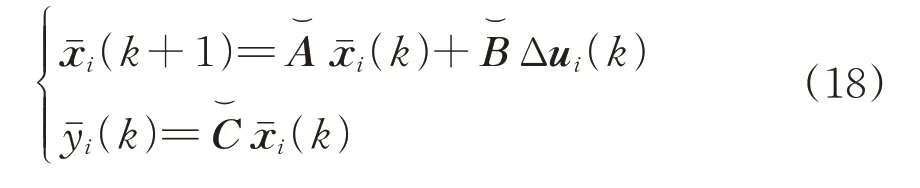
其中，

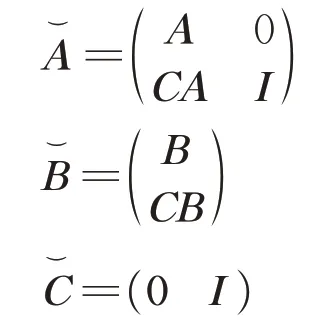
3.3 多步预测

在建立完预测模型后，将前后车时钟节点i 的相位偏移和频率偏移作为闭环系统的状态，通过调整闭环系统的控制输入量ui，通过实现前后车与参考时钟的时间同步，从而实现车车通信时间同步的目标。设时钟节点状态的预测步长为Np，在预测时域内控制量的控制步长为Nc，则未来Np个时间同步周期内使用Nc 个控制量，得到的前后车各时钟节点的状态预测值为

式中：k+1|k 为在第k 次同步周期时对第k+1 次同步周期的状态预测值。

同理，可以得到前后车各时钟节点从第k 次周期起Np个周期以内的输出预测值为

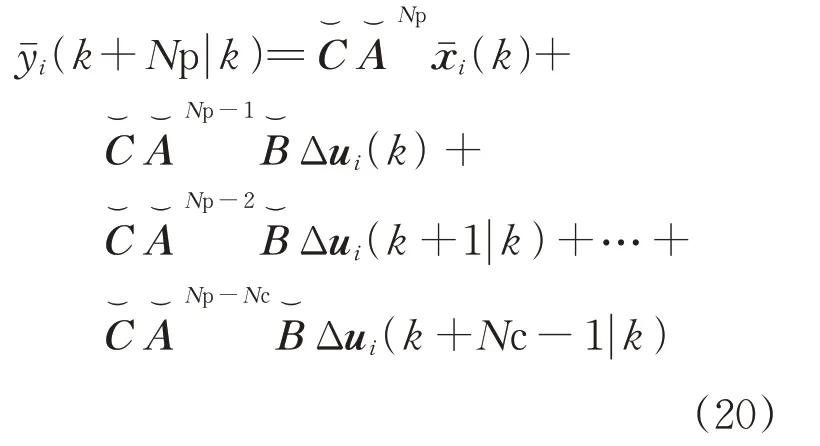
将式（20）进一步整合为矩阵形式，得到

其中，

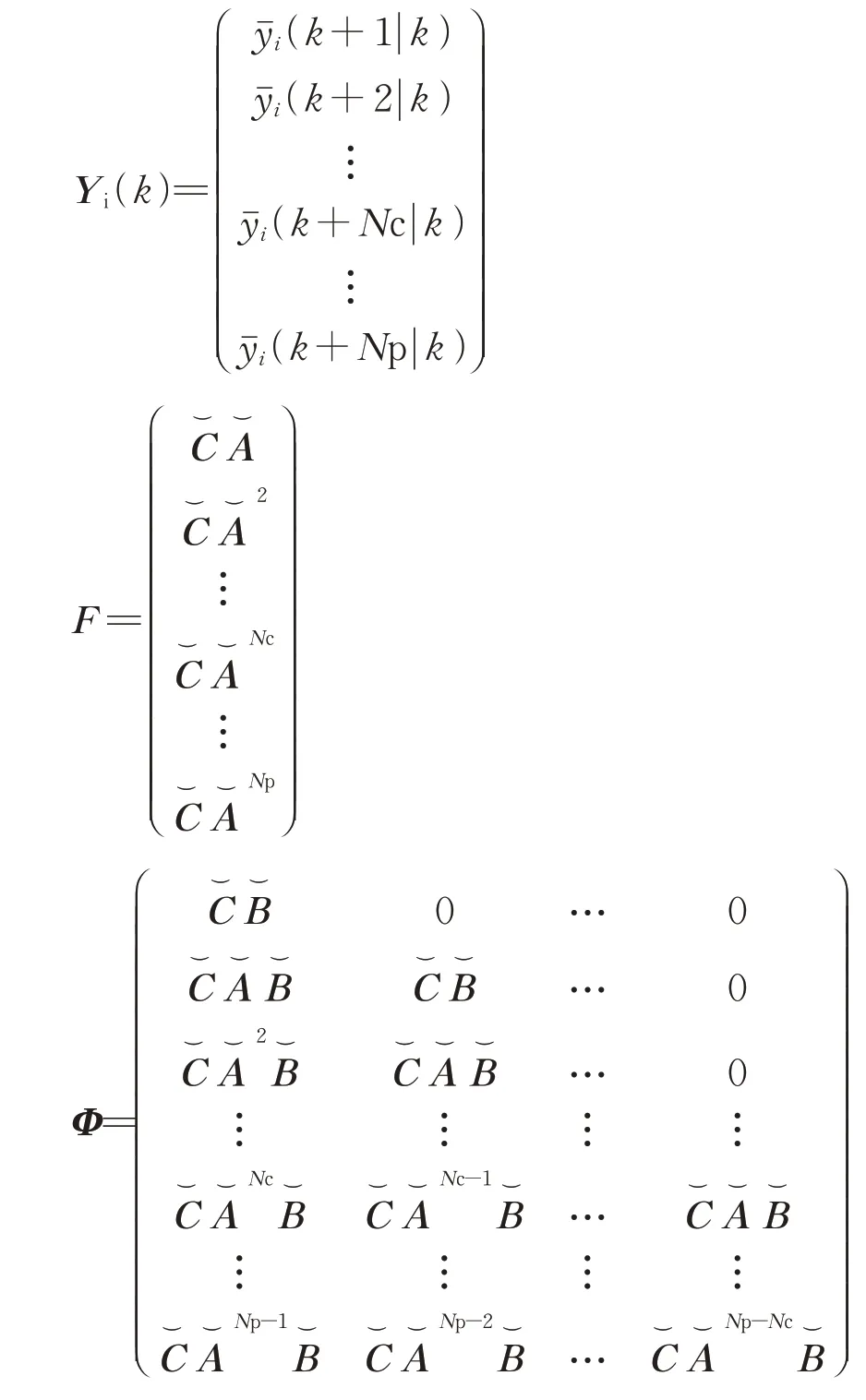
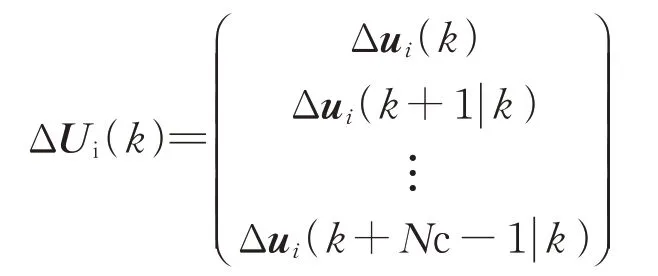
式中：Yi（k）为k+1 时刻起Np 步以内的预测输出矩阵；ΔUi（k）为k 时刻起Nc 步以内的控制输入增量矩阵；F和Φ分别为前后车时钟状态和控制输入增量ΔUi的系数矩阵。

3.4 滚动优化与反馈校正

最优控制输入增量Δu可通过最小化MPC的代价函数J 来求解。一般使用误差和输出增量的二次型矩阵作为代价函数，若gNB 提供的参考时间为R，则定义代价函数J为

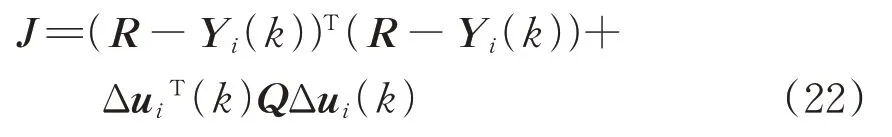
式中：等式右边的第1 项表示为参考输入R 与预测模型输出之间的误差，其值的大小反映了车车通信时间同步过程中前后车的同步性能；第2 项反映了车车通信时间同步过程的平稳性，其中Q 为对角矩阵，通过设置Q 的大小来限制控制输入增量Δu的值，以避免其值过大造成同步过程稳定性差的问题。

将式（21）代入（22）中，进一步将代价函数J 改写为

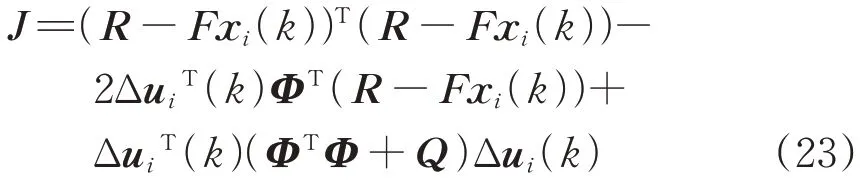
为了得到最优控制输入增量Δu，对式（23）中的Δu求1阶偏导，得到

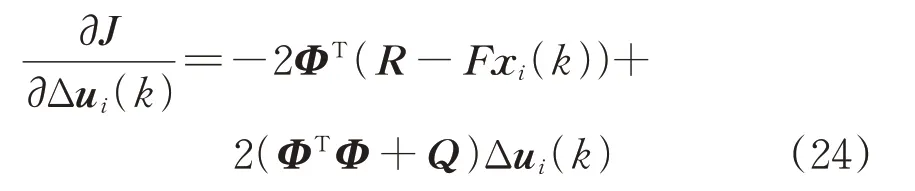
令J 的1 阶偏导数为0，可以求得前后车时钟在第k个同步周期的Δui（k）最优解为

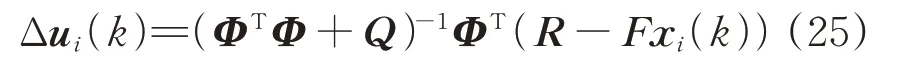
在5G-R 下车车通信时间同步过程中，由于存在端到端时延［22］，为了建立的模型能够更符合实际情况，需要进一步对式（25）中的时钟相位最优控制输入增量Δuiθ的值进行约束，为

式中：Δumax取端到端时延上限150 ms［22］。

最终，得到在第k 个同步周期时整个车车通信时间同步过程的最优控制输入量ui（k）为

式中：Δui（k）为最优控制输入增量。

得到第k 次同步周期最优控制输入量u 后，将其作为车车通信时间同步过程的反馈输入，进行该周期的反馈校正过程。不断迭代上述步骤，从而实现了5G-R 不同车车通信场景下前后车时钟节点对参考时钟的跟踪，继而完成5G-R 车车通信的时间同步。

4 仿真结果分析

为了验证本文方法对5G-R 下车车通信时间同步的有效性，采用MATLAB 软件分别对有中继和无中继场景下车车时间同步过程进行仿真试验。

4.1 有中继车车通信同步仿真分析

4.1.1 同步过程仿真

首先，对有中继场景下车车通信时间同步过程进行仿真。根据第三代合作伙伴计划（3rd Genera‑tion Partnership Project，3GPP）要求，将前后车初始时钟频率偏移α0i设为0.05 ppm［16］。5G-R 下车车通信时间同步过程的输入和输出扰动方差和设为5×10-11，5×10-8和10-6［23］。根据服务质量（Quality of Service，QoS）指标将丢包概率p 设为10-3。设闭环期望极点为P=（0.1 0.2），根据极点配置法可计算得到观测器增益矩阵L=（1.7 1.44）T。将仿真同步周期设为60 次，相邻前后车和其对应的中继站gNB 的本地时间分别设为0.4，0.2 和1 ms，得到基于MPC 的5G-R 有中继车车通信时间同步过程，如图5所示。

从图5 可以看出：随着同步周期的增加，gNB作为有中继场景下时间同步过程的参考时钟，其时间保持不变，而具有不同初始时间的前车和后车，随着同步周期的增加，二者时间均可以动态调整自身时间，并且在有限时间内逐渐调整校正到gNB参考时间，实现了前后车与gNB 参考时钟的一致性，继而完成了车车通信的时间同步过程。图5仿真结果说明使用本文方法能够完成5G-R 有中继模式下车车通信的时间同步。

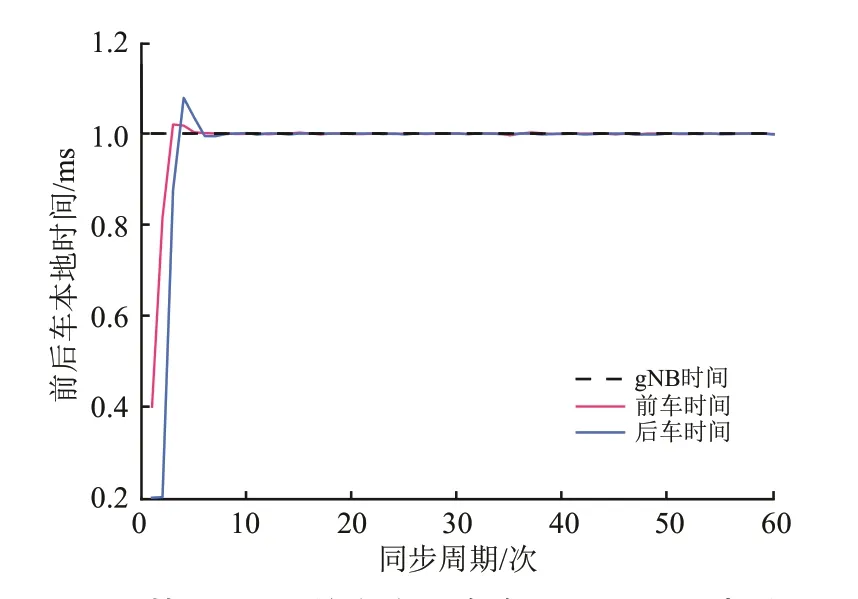
图5 基于MPC的有中继车车通信时间同步过程

4.1.2 同步性能比较

为了验证本文方法在有中继车车通信场景下的有效性，将本文方法与其他可适用于有中继场景下的文献［7］中基于PID 控制器的时间同步方法和文献［21］中基于误差增量的MPC 方法从收敛时间、时钟偏差以及系统稳定性3个方面进行比较。

首先是收敛时间方面的比较。收敛时间作为整个同步过程的最大逻辑时钟误差e →0 所需要的周期数，是评价时钟同步方法的重要的指标。为了便于比较不同方法对参考时间的跟踪能力，统一将文献［7］、文献［21］和本文方法列车的初始时间设为0 ms，将整个同步过程的参考时钟中继站gNB 的时间设为1 ms，得到用于有中继车车通信场景下的3种方法收敛情况如图6所示。

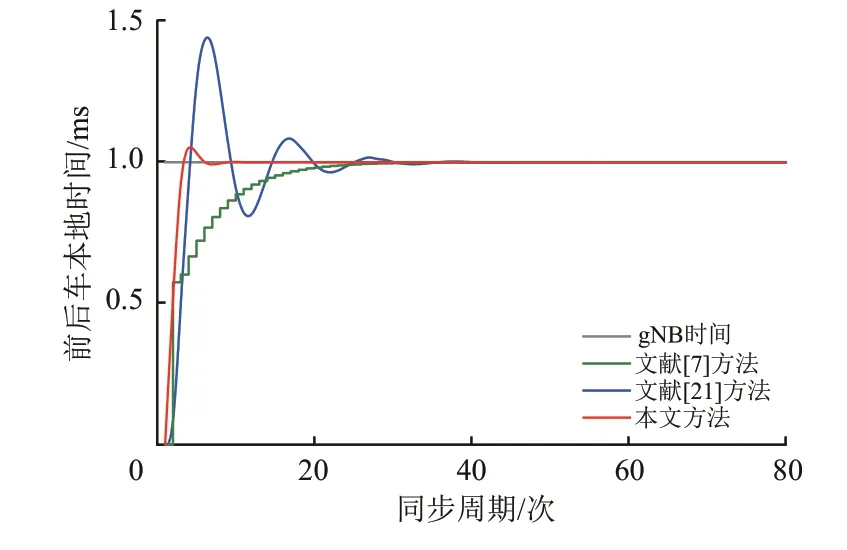
图6 有中继场景下的收敛性比较

从图6 可以看出：不同的比较方法实现前后车时间同步所需要的同步周期不一样；文献［7］基于PID 同步方法和文献［21］基于误差增量MPC方法大约在第40 个同步周期左右才能实现前后车与gNB的时间同步，而本文方法仅通过8个同步周期就达到收敛，其所需收敛周期为PID控制和误差增量MPC 控制的1/5，即本文方法同步收敛周期远小于另2种方法。这是因为文献［7］采用的PID控制方法适应快速时变的能力较差，易出现控制参数修改次数多、耗时长的问题［24］，因而其收敛速度较慢；文献［21］采用基于误差MPC 的同步方法在时间同步时以时钟误差为模型增量，但当时钟误差因5G-R 无线信道时变性以及数据包丢失等事件发生快速波动时，其控制量也会随误差变化发生快速震荡，导致该方法会出现收敛速度慢的问题；而本文方法由于综合考虑了数据包丢失和5G-R 信道时变性对同步过程造成的影响，相比于文献［7］和文献［21］的方法，能够更加快速地完成车车通信同步过程，具有更快的收敛速度。

其次是时钟偏差方面的比较。比较时，引入偏差平均值和偏差标准差进行量化比较，偏差标准差σ计算式为

式中：zi为输入值；为输入值的平均值；N 为样本数量。

由3 种方法得到的前后车之间时钟偏差的平均值和通过式（28）计算出时间偏差标准差，结果见表1。

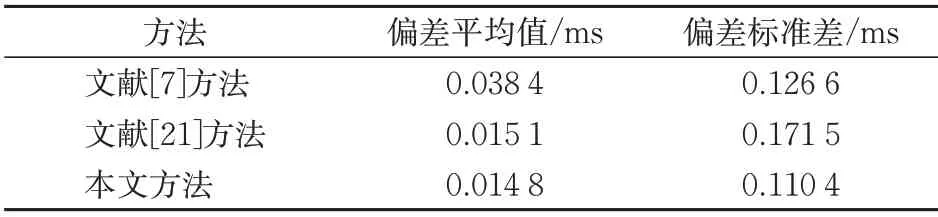
表1 不同方法得出的时钟偏差结果

由表1 可知：文献［7］和文献［21］方法得到的时钟偏差平均值均大于本文方法；偏差标准差作为反映样本间离散程度的指标，其值越小表示时钟同步误差越小，越接近于标准参考值，因此本文方法的偏差标准差较其他2 种方法来说最低，从而说明本文方法具有更低的同步误差，其同步精度更高。

最后是系统稳定性方面的比较。系统控制输入增量Δuiθ的变化情况反映了系统的稳定程度，不同方法在有中继场景下的系统稳定程度如图7所示。

从图7 可以看出：本文方法中MPC 控制器的控制输入增量Δuiθ随着同步周期的增加而快速趋于稳定；而文献［7］和文献［21］方法由于没有考虑到在同步过程中数据包丢失会带来一定的时钟误差影响，导致文献［7］和文献［21］方法的控制输入增量Δuiθ出现了剧烈的波动现象；本文方法能够有效地保证有中继场景下车车通信时间同步过程的稳定性。

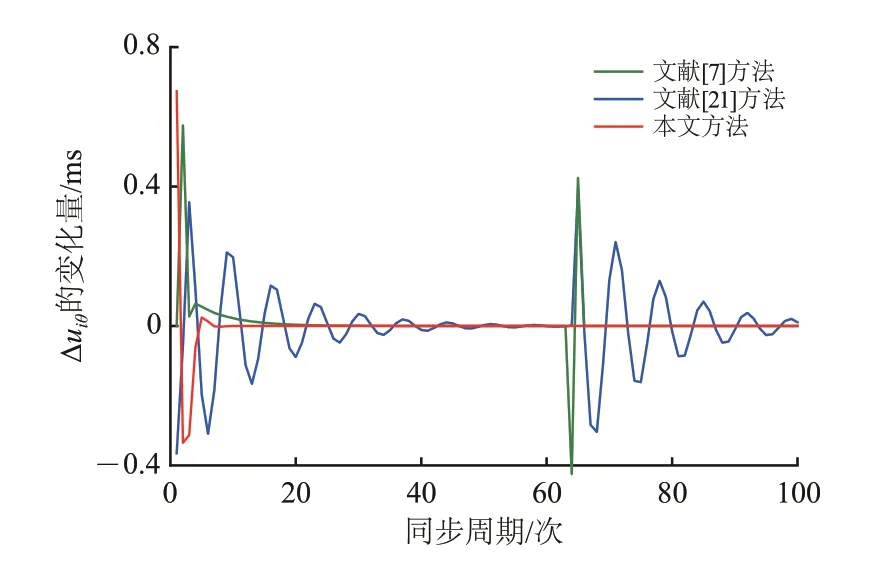
图7 有中继场景下的系统稳定性比较

在有中继车车通信模式下，通过上述收敛时间、时钟偏差以及系统稳定性3个方面的分析，可以综合得出：所提方法相比于比较方法，能够更有效地完成5G-R有中继模式下车车通信时间同步。

4.2 无中继车车通信同步仿真分析

4.2.1 同步过程仿真

在完成有中继模式下车车通信同步分析后，对无中继车车通信场景下时间同步过程进行仿真分析。由于无中继场景下缺少提供标准参考时钟的gNB 中继站，因而在无中继场景下需要设置1个虚拟参考时钟，作为前后车同步的主时钟，前后车通过对虚拟参考时钟进行跟踪，来完成前后车之间的时间同步。

将仿真同步周期设为10 次，前后车初始时间继续设为0.4 和0.2 ms，将动态系数β 设为0.4，仿真得到本文所提方法在无中继车车通信时间同步过程，如图8所示。

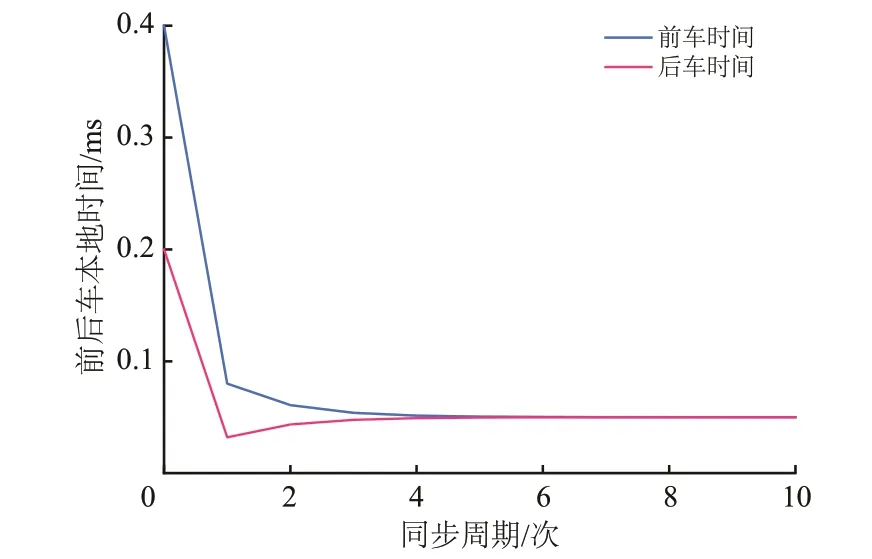
图8 无中继场景下车车通信时间同步过程

从图8 可以看出：随着同步周期逐渐增加，本文方法能够在没有物理参考时钟的情况下，通过相邻列车时间信息交互动态调整自身的时钟状态，将具有不同初始时间的前后车时钟，在有限时间内完成时间同步，从而实现了无中继场景下车车直接通信的时间同步过程。

4.2.2 同步性能比较

为了验证本文方法在无中继车车通信时间同步过程的有效性，从收敛时间和时钟偏差2 个方面进行性能分析，并与文献［14］中的无中继场景同步方法进行比较。为了便于比较分析，将文献［14］和本文方法中前车初始时间均设为0.4 ms，将后车的初始时间均设为0.2 ms。

首先对无中继模式下不同方法的收敛时间进行比较，仿真得到无中继车车通信场景下收敛时间比较结果，如图9所示。

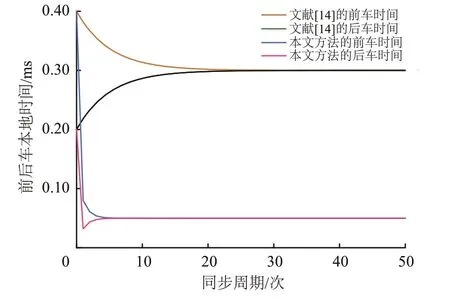
图9 无中继场景下收敛时间比较结果

从图9 可以看出：文献［14］采用基于平均一致性的时间同步方法，该方法在30 个同步周期内实现了车车之间的时间同步，而本文所提基于MPC 的同步方法仅在5 个同步周期内就实现前后车的时间同步，大大缩短了收敛时间；上述收敛时间较大差异，主要原因是文献［14］采用一致性理论作为其同步方法，而一致性理论作为1种分布式协同方法，其实现全局一致性主要借助于输入控制量的值，该值主要根据其相邻节点的局部信息计算得到［25］，而5G-R 无线信道带来的不确定输出扰动会对该控制量值带较大的影响，因此会出现其收敛时间较长的问题；而本文方法通过相邻列车时间信息交互来动态调整自身时钟，具有更好同步协同性和更快的收敛速度。

最后，进行无中继模式下车车通信前后车时钟偏差方面的比较，可以仿真得到前后车时钟之间时间偏差的比较结果，如图10所示。

从图10可以看出：在无中继模式下，2种方法随着同步周期的增加，其前后车时钟偏差均可以逐渐减小，并逐步收敛；文献［14］方法未能实现真正意义上的时间同步，其前后车时钟之间仍存在一定时钟偏差；而本文方法前后车时钟偏差为0，说明本文方法具有更高的同步精度，更好地实现了5G-R 无中继场景下车车高精度时间同步，能够满足5G-R下车车通信时间同步精度要求［16］。

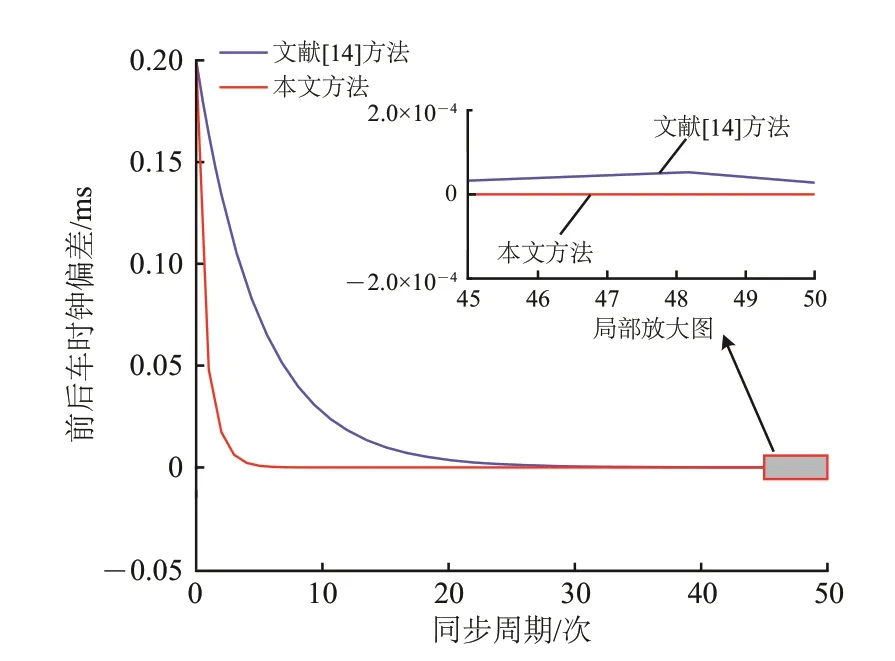
图10 无中继场景下前后车时钟偏差比较

在无中继车车通信模式下，通过上述收敛时间和时钟偏差分析，可以得出在无中继模式下，相比于比较方法，所提方法具有更快的收敛速度和更高的同步精度，能够更好地实现5G-R 无中继车车通信时间同步。

4.3 不同时延抖动对同步过程的影响

进一步分析5G-R 时延、抖动对本文时间同步过程的影响。首先进行5G-R 时延影响性分析，为了便于比较不同时延对同步过程的影响，根据5G-R下数据包时延范围［26］，取时延19，56 和100 ms，仿真得到本文方法控制输入增量Δuiθ随同步周期的变化情况，如图11所示。

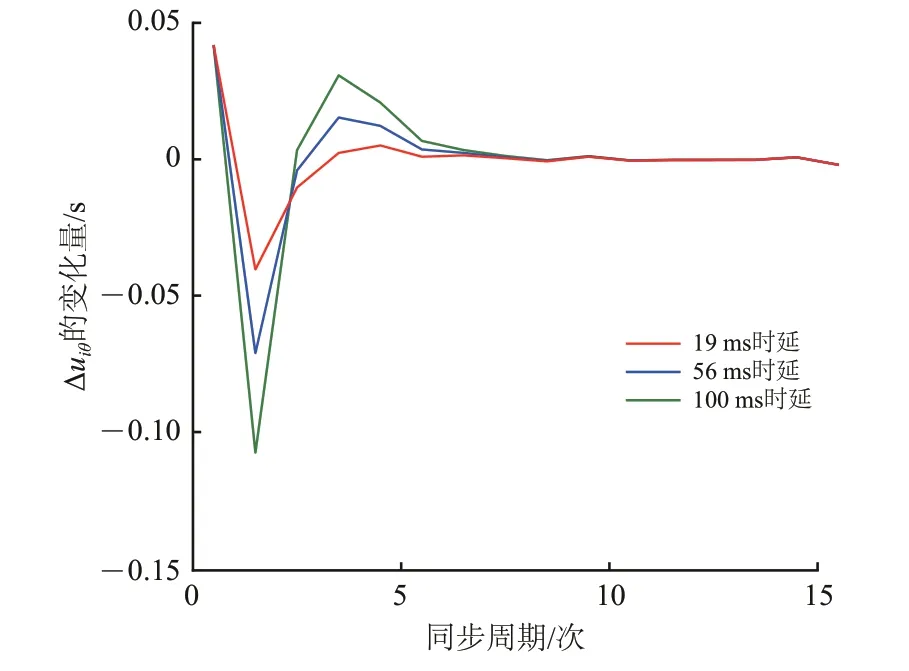
图11 不同时延对同步过程的影响

从图11可以看出：5G-R 时延越大，控制输入增量Δuiθ的变化幅度也越大，而控制输入增量Δuiθ代表了系统的稳定程度，这说明时延的大小能够影响5G-R 下时间同步过程的稳定性，时延越大，同步过程越不稳定；随着同步周期的增加，控制输入增量Δuiθ值逐渐趋于平稳，说明本文方法能够有效消除时延对同步的影响，进一步验证了本文方法的有效性。

然后，进行5G-R 传输抖动对同步的影响性分析。PTP 同步报文在高速铁路时变信道上传输时，会存在一定的传输抖动，造成PTP 协议链路传输不对称。将初始列车时钟设为20 ms，参考时钟为50 ms，将传输抖动设为随机噪声，通过不同的噪声方差值，继而得到不同抖动对同步过程的影响结果，如图12所示。

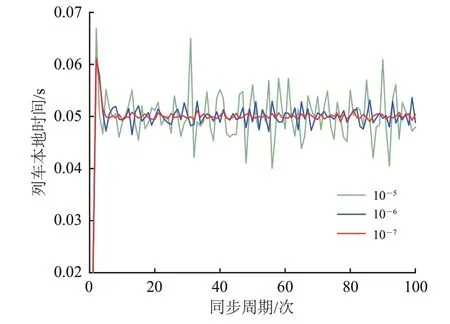
图12 不同抖动对同步过程的影响

5 结 论

（1）本文提出了1种基于模型预测控制（MPC）的5G-R 下车车通信时间同步方法。通过构建前后车时钟MPC 控制器，使用多步预测、滚动优化和反馈校正等控制手段，实现了5G-R 下车车通信的时间同步。

（2）针对现有同步方法易受报文丢失影响导致同步精度低和收敛速度慢的问题，引入了观测器方程对丢包时的前后车时钟状态进行估计，降低了因丢包带来的时钟误差对同步过程造成的影响，提高了车车通信同步精度。

（3）通过在有中继和无中继2 种车车通信场景下进行仿真试验表明，本文方法能够实现不同场景下的车车通信时间同步。

（4）相比其他方法，本文方法在有中继模式和无中继模式下，均具有更快的收敛速度和更高的同步精度。本文研究结果对5G-R 无线通信下车车同步通信提供了一定的理论参考依据。