基于开孔面积的高海拔隧道风管漏风率研究

陈湛文，王明年，郭佳城，秦鹏程，严 涛，韩常领

（1.西南交通大学 土木工程学院，四川 成都 610031；2.西南交通大学 交通隧道工程教育部重点实验室，四川 成都 610031；3.中交第一公路勘察设计研究院有限公司，陕西 西安 710075）

随着我国隧道建设技术进步和西部地区交通行业发展的需求，出现了越来越多的长大高海拔隧道。隧道施工中，爆破、出渣、喷射混凝土等工序及施工机械尾气排放产生大量的粉尘和有毒有害气体，对隧道内作业人员的生命安全造成极大危害。而施工通风作为隧道内外空气交换的唯一手段，对于改善隧道内施工作业环境和保障作业人员安全起着至关重要的作用。

当前，对于隧道施工通风已在需风量、风机效率、风机选型、施工供氧及通风降温等方面［1-5］进行了相应研究，但现场测试结果反映出隧道掌子面处仍出现需风量不足的现象，而风管漏风是导致出现该现象的首要原因之一，开展高海拔隧道施工通风风管漏风率的相关研究显得迫在眉睫。

目前，国内外众多学者针对风管漏风率进行了一定程度的研究。其中，Holdsworth 等人［6］对管道内流量与压力梯度、泄漏率与超压之间的幂律关系进行分析，并利用包含管道阻力常数和泄漏常数的诺模图进行计算验证；Alvarez 等人［7］基于显式方法开发了一种简易的计算机程序对隧道通风系统进行计算，并通过现场测量方法校准修正以提高计算精度；Auld［8］在借鉴Atkinson 方程基础上分析了管道直径、管道摩擦系数以及管道流量变化等多重因素对管道泄漏的影响，引进“风管效率”的概念量化泄漏对通风管道性能的影响，并采用电子表格法对泄漏系数进行量化；黄宽渊等人［9］将管道接头漏风视为孔口流，通过建立漏风管的数学模型对漏风率与静压、漏缝尺寸、管段水力特性等因素间的关系展开分析，并提出“综合漏风参数”以此表征风管的漏风特性及管段特性；李琦等人［10］基于流体力学理论分析了海拔高度对隧道风管漏风率的影响程度，并推导出高海拔地区风管漏风率修正系数，采用现场实测数据验证了理论计算结果的合理性；曹正卯［11］通过模型试验得到不同初始风速和不同风管弯曲角度工况下的风管百米漏风率，并推导出风管弯曲角度对风管漏风率影响系数的计算式。王晓亮［12］通过理论分析和现场测试对基于风机性能的风管漏风率计算方法进行相关研究，并采用MATLAB 软件对漏风率数据进行拟合，得到在不同风压与需风量下的百米漏风率计算式。上述研究主要是基于海拔高度、风机性能及风管弯曲角度等因素对隧道风管漏风率的影响程度展开研究，而开孔面积对风管漏风率影响的分析相对较少。

本文采用理论推导、数值模拟和现场实测等手段，针对高海拔隧道开孔面积对风管漏风率的影响展开研究，从而保障高海拔隧道的施工安全和有效提高施工效率。

1 风管漏风作用机理

对于通风风管本身而言，风管制作工艺和现场拼接并不能使其完全密封，且隧道施工中风管受爆破出渣、二衬台车擦刮等偶然因素的影响，风管出现破损漏风是客观存在的。

1.1 假设条件

为简化风管漏风机理的理论推导，基于流体力学理论做出以下初始假定。

（1）将隧道风管内流动气体视为连续性介质，即内部质点之间无间隙；

（2）由于空气在流动过程中密度变化很小可忽略不计，可将风管内流动气体视为不可压缩流体，即无黏性流体；

（3）风管研究段全程等截面，其材料特性及几何尺寸保持不变，且保持风管平滑顺直，不考虑弯曲角度和坡度对漏风率的影响；

（4）隧道风管内外温差保持不变，且温差不随风管长度增加而发生变化，不考虑空气热传递对风管漏风率的影响；

（5）隧道风管漏风计算只考虑风管破损处，不考虑风管各段连接处及风管材料自身密封特性。

1.2 隧道单段风管漏风率

为了对风管漏风机理进行量化，利用流体力学理论，将风管视为均匀送风管道，采用静压复得法［13］对风管漏风率展开计算。

新鲜风在管道内输送中，气体全压由静压pj和动压pd组成。当风管侧壁存在漏风孔时，风管内外气体静压差作用使得气体从孔口流出而产生漏风［9］。漏风孔处气体出流风速大小和方向由静压和动压两者产生的流速和方向共同决定，使得气体出流方向发生偏斜，气体流速为静压和动压的矢量合成流速，如图1 所示。图中：vj和vd分别为气体静压流速和动压流速，m·s-1；v 为合成流速，m·s-1；θ 为漏风孔出流角；A 为孔口在风管轴向上的投影面积，m2，A0为漏风开孔面积，m2。

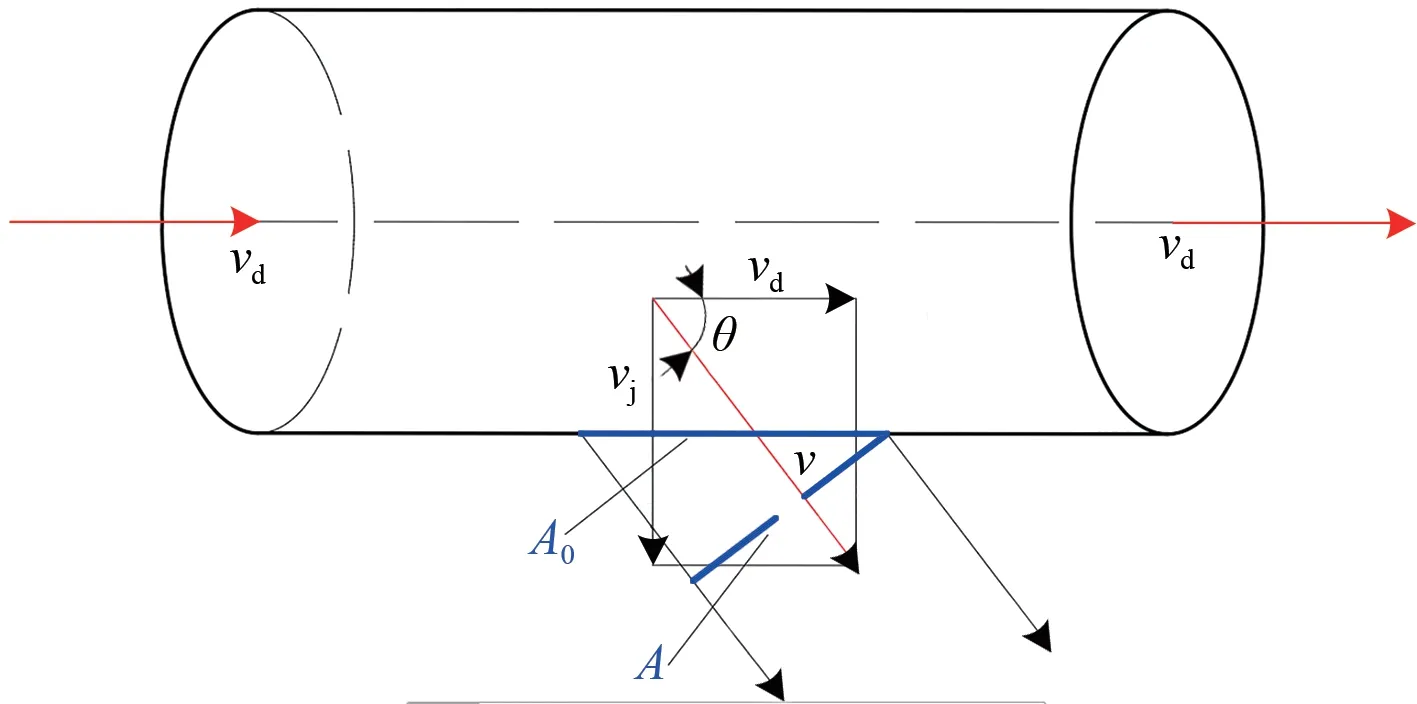
图1 风管孔口出流示意图

风管气体静压和动压所产生的流速计算式为

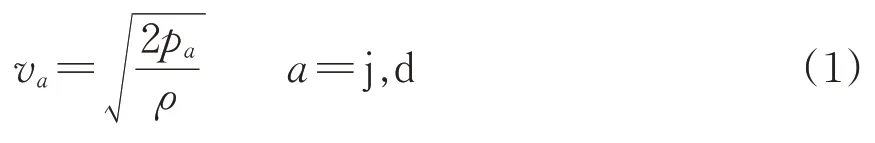
式中：va为气体静压流速或动压流速；pa为风管内气体静压或动压，Pa；ρ为气体密度，kg·m⁻3。

则漏风孔气体流速v为

单位小时孔口漏风量q0为

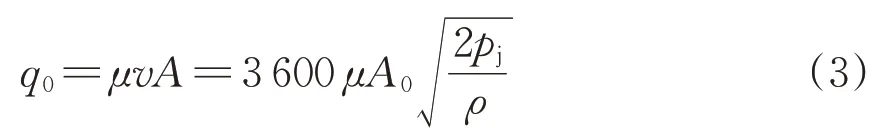
式中：μ为孔口流量系数。

式（3）表明：单位小时风管孔口漏风量q0主要与开孔面积A0、气体静压pj（由风机初始风量和风压所决定）及空气密度ρ 这3 个变量相关，且q0与A0和pj均呈正相关，与ρ呈负相关。

1.3 隧道沿程风管漏风率

随着隧道掌子面施工进程的增加，风管长度也随之不断增长，整个施工通风过程中各段风管漏风量并非一直保持恒定的，而是随着距风机距离的增加而不断发生变化，故还需在上述基础上对风管沿程各段漏风率变化特征进行分析研究。根据恒定总流的伯努利方程和能量守恒方程，其漏风率计算如图2 所示。图中：Qn-1，Qn和Qn+1分别为第n-1段、第n段和第n+1段风管内风量；Q'n和Q'n+1分别为第n段和第n+1 段的漏风量；Ej，n和Ed，n分别为断面n的静压能和动压能；Ej，n+1和Ed，n+1分别为断面n+1 的静压能和动压能；ΔEn~n+1为从断面n至断面n+1 的流动能量损失，其由摩擦阻力fh和局部阻力fm引起的能量损失构成。

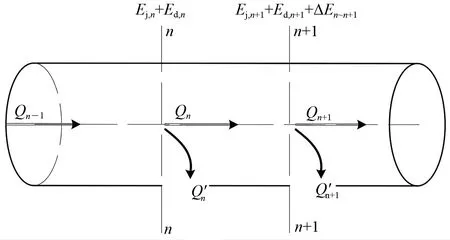
图2 风管能量守恒计算示意图

则风管各分段的能量守恒方程式为

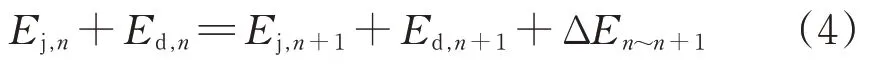
其中，

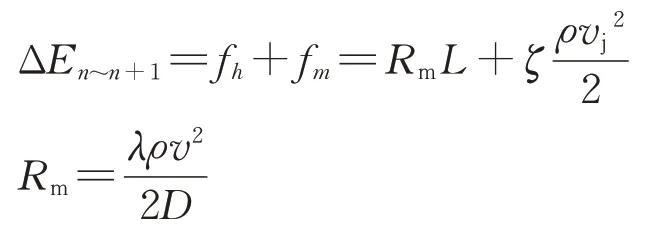
式中：Rm为比摩阻，Pa·m⁻1；λ为摩擦系数，根据现场实测经验取值为0.012~0.015［14］；D为风管直径，m；L为风管均等分段长度，m；ζ为空气流过侧孔直通部分的局部阻力系数。

空气流过侧孔直通部分的局部阻力系数取值［14］见表1。表中：vn+1为风管计算断面n+1 流速；vn为断面n流速。

表1 空气流过侧孔直通部分的局部阻力系数ζ取值

结合上述风管漏风机理和流体力学理论，将通风风管等长均分为k段，则可推导得出第i（i=1，2，…，k）段风管漏风率ηi的计算式为

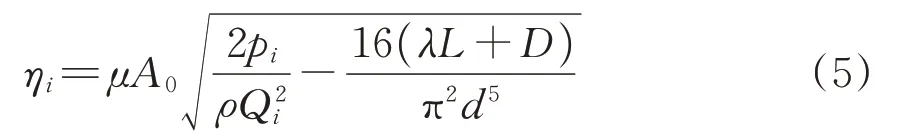
其中，

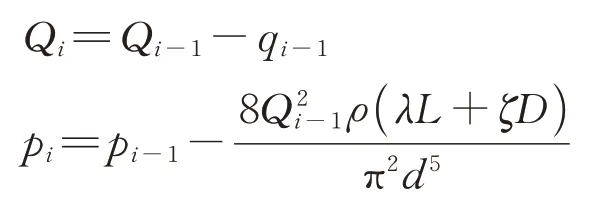
式中：ηi为第i段风管漏风率，%；Qi为第i段风管内风量（第1 段风管风量Q1即为风机初始风量），m3·s-1；qi-1为 第i-1 段风 管漏风量，m3·s-1；pi为第i段风管内气体全压，Pa，其为前1 段风管内的气体全压减去沿程阻力和局部阻力（第1段风管全压p1即为风机初始风压）。

综上，理论推导了隧道风管漏风量和沿程各段漏风率的计算式，明确了风管漏风率的影响因素主要为海拔高度、漏风开孔面积以及风管静压（即风机性能）。由于李琦等［9］和王晓亮［11］已经针对海拔高度和风机性能对风管漏风率的影响进行了相应研究，本文重点研究开孔面积对风管漏风率的影响规律。

1.4 风管漏风率理论计算

结合上述隧道风管沿程各段漏风率计算式，在平原和高海拔地区环境下，依托海拔高度3 850 m的巴朗山隧道，开展考虑海拔高度和漏风开孔面积2种因素的风管漏风率计算。

计算过程中，将风管分为m段，每分段长度取100 m，分别计算风管各分段漏风率。平原和高海拔隧道环境及尺寸参数见表2。

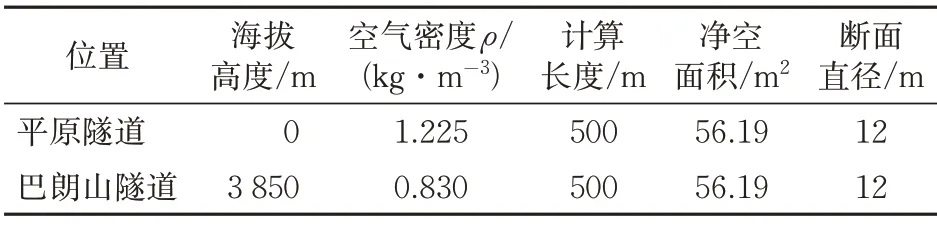
表2 平原和高海拔隧道环境及尺寸参数

选取SFD-No14 型轴流风机性能参数作为风机计算参数，详见表3。

表3 SFD-No14型风机参数

选取拉链式软风管作为风管类型，设计参数见表4。

表4 风管设计参数

采用控制变量法，分别选取风管漏风开孔面积0.04，0.06 及0.08 m2这3 种工况，在保持风机性能参数（风量及风压）不变的情况下，计算得到不同漏风开孔面积工况下平原和高海拔地区隧道风管沿程各分段漏风率变化特征如图3所示。

图3 不同漏风开孔面积下风管漏风率变化

由图3 可知：平原地区不同漏风开孔面积的平均百米漏风率处于1.54%~3.24%，高海拔地区（巴朗山隧道）处于2.04%~4.31%；其证明了前人得出的风管漏风率随海拔高度增大而升高的结论，且高海拔地区各工况平均百米漏风率约为平原地区的1.33倍。

此外，漏风开孔面积的增大将致使风管漏风率以不同斜率的幅度变化，除了平原地区开孔面积较小时漏风率沿程降低以外，其余工况均随着开孔面积的增大而升高，且开孔面积越大，漏风率升高幅度越大。

因此，隧道施工工程中应对风管产生开口破损引起足够重视，定期检测和及时采取应对措施，否则将对隧道通风产生巨大影响。

2 风管漏风率数值模拟

运用Fluent软件，保持前述理论分析中选取的隧道、风机及风管参数不变，采用数值模拟方法，研究平原地区和高海拔地区不同漏风开孔面积工况下风管百米漏风率的变化规律，亦可验证理论计算得出的结论。

2.1 计算理论及基本假定

考虑到高海拔隧道长距离通风所需风量较大，隧道风管采用基于Navier-stokes 方程的三维非稳定不可压缩通风模型，并采用RNG k-ε 湍流模型封闭方程进行模拟。计算中的基本假定［15］如下：

（1）风管气流为连续介质的非稳态紊流，可假定为三维黏性不可压缩流体；

（2）隧道施工通风中忽略由流体黏性力做功产生的耗散热，即隧道中无能量交换；

（3）气体视为非稳态等温流体，在考虑隧道内气流随时间变化过程前提下，假定隧道内污染源分布较为分散。

2.2 模型建立

由于隧道内气体流动的复杂性和不确定性，仅采用二维计算模型并不能准确描述气体在隧道内的扩散，故此处应采用三维数值模拟模型进行计算［16］。模拟中采用Fluent软件内置的Design Mold‑er 模块对隧道和通风风管进行参数化建模。其中，采用巴朗山隧道实际尺寸（表3所示）进行隧道建模；风管模型设置于隧道模型拱顶位置，且进风口设置于隧道洞口30 m 以外，送风口设置于距掌子面15 m 处；并采用Fluent 软件DM 模块中的Face Split 工具在风管底部距隧道入口每隔100 m 设置1个圆形漏风孔，共设置5个截面位置的漏风孔。同时，利用内置的Mesh 模块对隧道模型及风管模型进行网格划分；网格采用非结构化网格，且可由软件自动细化各分段风管漏风孔附近的网格，隧道及风管模型图如图4所示。

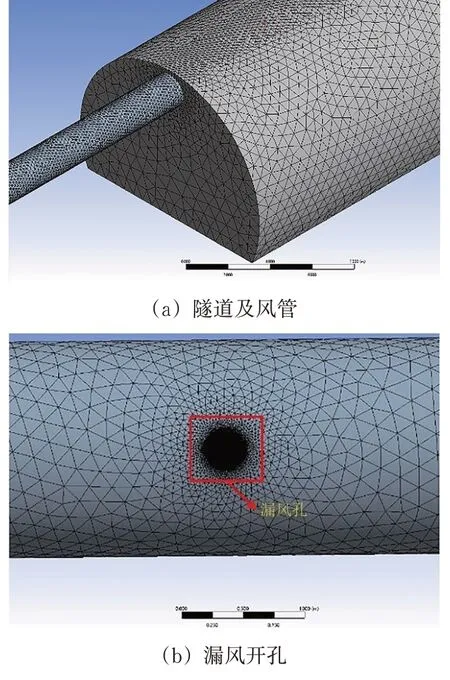
图4 隧道与风管模型示意图

2.3 初始及边界条件

数值模拟中选取设定的初始与边界条件如下。

（1）此模拟所选取的风机参数见表3，即选取初始风量为4 200 m3·min-1，初始风压为1 630 Pa，风管内壁面摩擦系数0.002 3。

（2）隧道风管入口设置为速度入口边界，入口风速为27.51 m·s-1，风速方向沿入口法线方向，风管出口为系统默认边界。

（3）风管漏风口设置为系统内部边界。

（4）风管和隧道内壁的边界类型均设为固定边界，满足无滑移条件，其风速为0。

2.4 工况参数

设置6 个工况分析平原地区和高海拔环境下漏风开孔面积对风管漏风率的影响，工况参数详见表5。

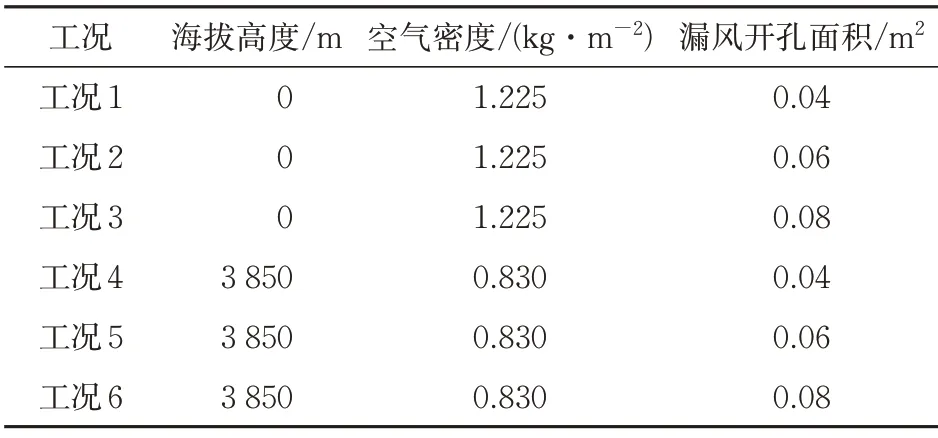
表5 不同风管漏风影响因素模拟工况

2.5 模型网格敏感性分析

为了验证漏风率数值计算结果的准确性和可靠性，本文通过选取4种不同规模的网格单元数，分别为875 万、669 万、437 万及271 万个，开展隧道及风管模型的网格敏感性分析。以工况6（漏风开孔面积为0.08 m2）为例，4 种不同网格单元数计算得到的各分段漏风截面风速如图5所示。

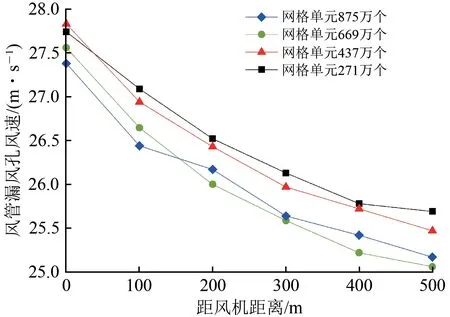
图5 不同网格单元敏感性分析

图5 反映了不同网格单元精度下，漏风开孔面积为0.08 m2时各分段风管漏风孔截面的平均风速。通过数值计算得知，不同网格单元精度的隧道及风管模型所计算得到的漏风截面风速略有不同。可以发现，隧道及风管模型整体网格单元数为271万和437 万个时，其计算出的漏风截面风速与网格单元数为669 万和875 万个时的风速相差较大；且当网格单元数为669 万个时，计算结果与网格单元数为875万个时相差较小。

因此，选择669 万个网格单元作为此次数值模拟的单元数，其计算得到的漏风风速较为合理，既能保证计算结果精度且计算时间也相对较短。此时隧道及风管模型被划分为6 697 861 个单元，风管模型为2 611 657 个单元，隧道模型为4 086 204 个单元。

2.6 计算结果提取

以上述确定的网格单元数669 万个作为计算依据，开展平原和高海拔地区不同开孔面积风管漏风风速计算，提取不同开孔面积下100 m 截面处的风管漏风截面速度云图，计算结果显示平原地区与高海拔地区不同开孔面积对漏风孔风速分布的影响趋势基本一致，因此只列出高海拔地区计算结果如图6所示。

由图6 可知：3 种不同开孔面积工况风管漏风孔处的湍流速度场分布大体一致，但3种工况的漏风孔处的泄漏速度则有所不同，开孔面积0.04，0.06 和0.08 m2对应的最大泄漏风速分别为48.45，47.25 和46.81 m·s-1，漏风开孔面积越小则从孔口溢出风速越大。

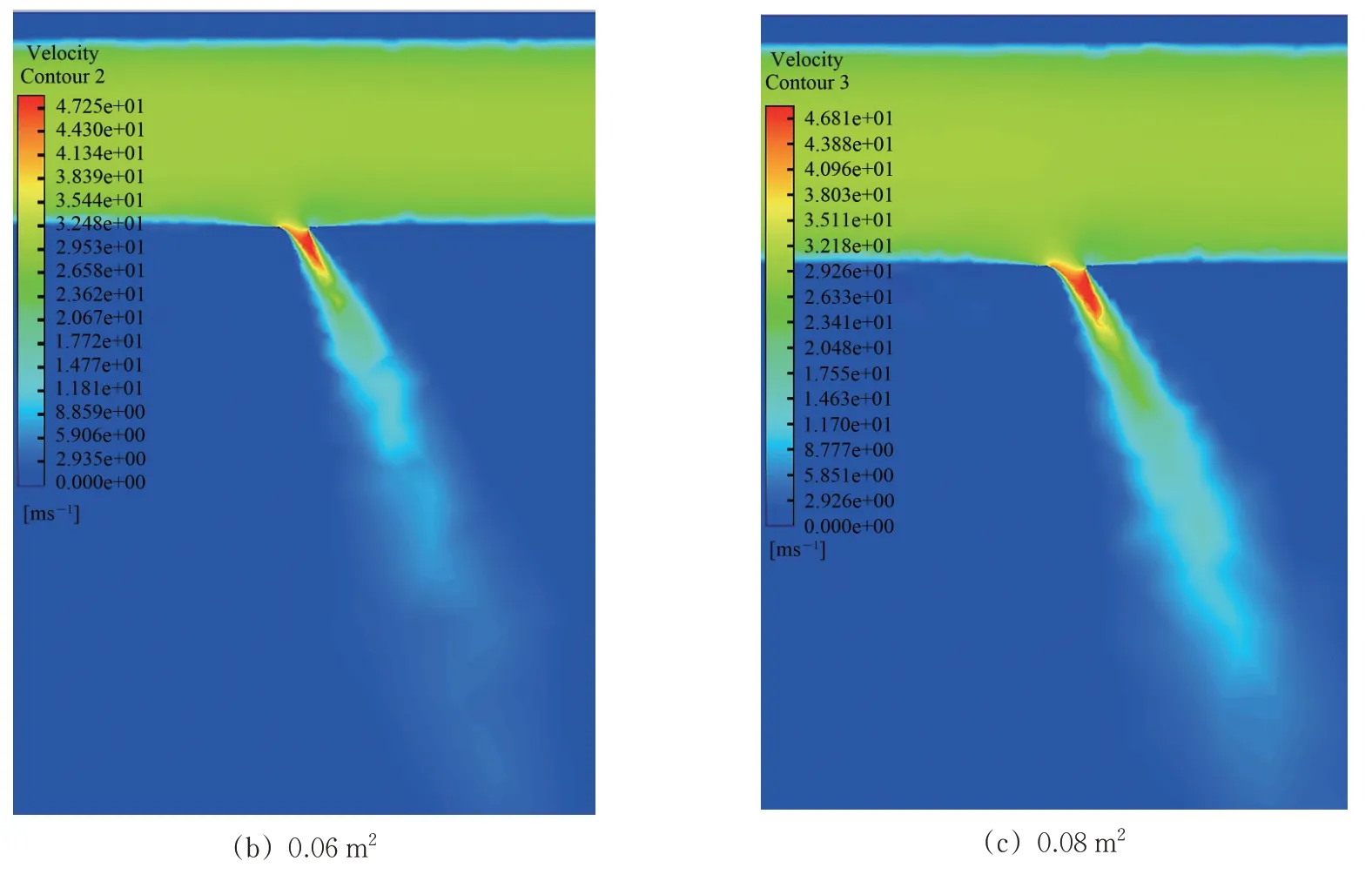
图6 高海拔地区不同开孔面积的漏风孔风速分布（100 m截面处）

为得到各工况不同漏风孔位置处的断面平均风速从而进一步分析漏风率变化规律，利用Fluent软件的CFD-Post 后处理平台，采用面积积分法获取得到平原和高海拔地区不同漏风开孔面积工况的风管各段漏风孔截面平均风速分别见表6和表7。

表6 不同工况风管各段漏风孔截面平均风速（平原地区）

表7 不同工况风管各段漏风孔截面平均风速（高海拔地区）

2.7 数值计算结果

根据上表得到的漏风孔截面平均风速，通过下述百米漏风率计算式［17］得到不同开孔面积工况沿程各分段的截面漏风率为

式中：η100为百米漏风率，%；Q0为风机进风量，m3·s-1；Q1为风机有效风量，m3·s-1；l为风管长度，m。

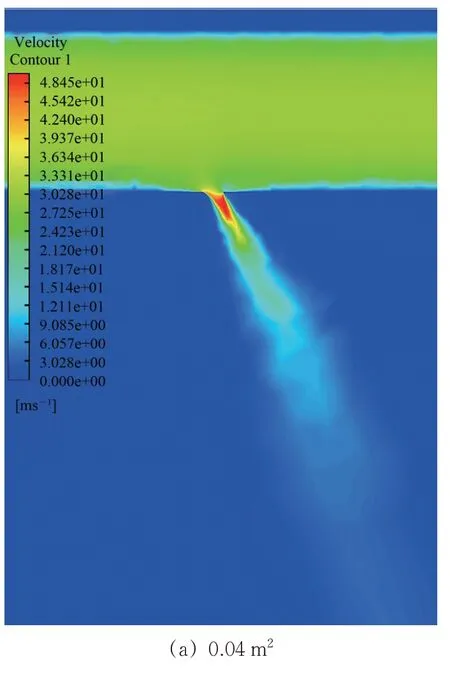
则可计算得到平原和高海拔地区隧道不同漏风开孔面积工况下的各分段截面漏风率如图7所示。

由图7 可知：数值模拟所计算得到的平原地区风管不同漏风面积下百米漏风率为1.57%~3.41%；高海拔地区（巴朗山隧道）为2.36%~4.21%，高海拔地区同样约为平原地区的1.33 倍，风管漏风率随漏风开孔面积的增加而变幅度升高。

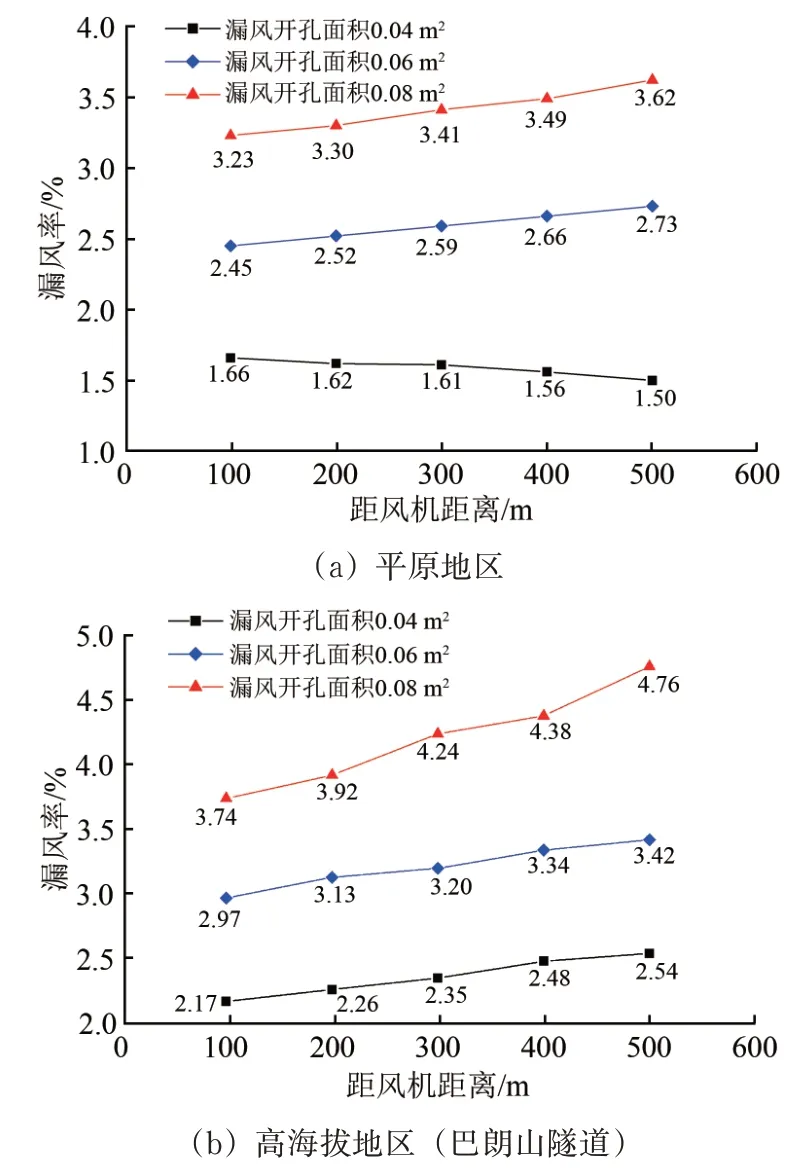
图7 不同漏风开孔面积工况下的风管截面漏风率

同时，通过与前述图3 理论计算数据比较可知，数值模拟计算得到的风管漏风率相对较大，但漏风率总体变化趋势与理论分析结果相互吻合。这也进一步证明了风管漏风计算原理的合理性和适用性，以及漏风开孔面积这一因素对于高海拔隧道施工通风的重要影响。

3 基于开孔面积的风管漏风率系数修正

前述李琦等人［10］仅对隧道风管漏风率开展海拔高度修正计算，下文将结合上述高海拔地区理论和数值计算结果开展风管漏风率基于开孔面积的修正，并推导得出开孔面积修正系数的计算公式。

依据《铁路隧道工程施工技术指南》中所规定百米漏风率不超过1%的规定［18］，选取1%作为本文风管漏风率修正的基准值，将不同开孔面积的平均百米漏风率与基准的漏风率之比定义为风管漏风率的开孔面积修正系数，其计算式为

式中：c1为风管漏风率的开孔面积修正系数；η100为不同开孔面积的平均百米漏风率，%；η0为风管漏风率的基准值，即为1%。

为增加开孔面积修正系数这一样本量，在前述计算结果上增加开孔面积0.02 和0.10 m2这2 组工况，计算得到其对应的平均百米漏风率分别为1.00%和5.55%。不同开孔面积的风管漏风率开孔面积修正系数见表8。

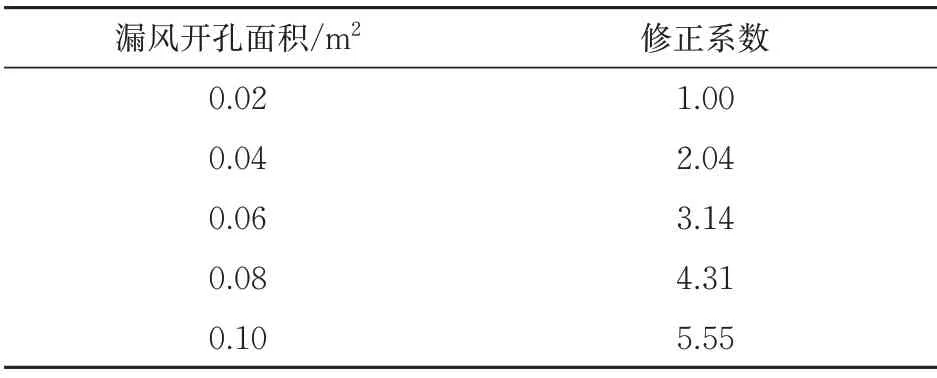
表8 风管漏风率的开孔面积修正系数

根据上表可运用Origin软件进行线性拟合得到漏风开孔面积和风管漏风率的开孔面积修正系数之间的关系如图8所示。图中：R2为相关系数。

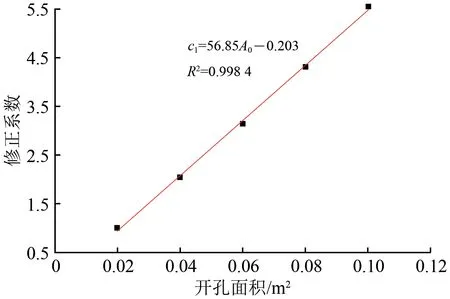
图8 风管漏风率开孔面积修正系数曲线

由图8 可知：风管漏风率随开孔面积增大的修正系数理论模型为

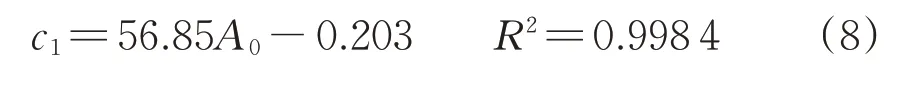
4 高海拔隧道风管漏风率现场实测

为验证上述开孔面积对风管漏风率的影响规律，对更换风管前后的漏风率进行现场测试分析。

测试地点选取在四川省海拔3 850 m 的巴朗山隧道；漏风率测试段分别选取于巴朗山隧道入口段400 m（映秀端）与隧道出口段850 m（小金端）。映秀端主洞风机型号为SFD-No12.5，小金端则为SFD-No14，测试中风机档位均设置为高速，2 类风机高速档位下的技术性能参数见表9。

表9 施工通风机技术性能

本测试中更换风管前后的通风风管均选取目前国内常用的PVC 拉链式软风管，其中映秀端风管直径为1.5 m，小金端风管直径为1.8 m。本测试中将风管各测试断面分为若干等面积圆环，并采用对数线性法确定测试截面各测点距对风管壁的距离，进而可通过测试得到各断面平均风速和百米漏风率。

结合巴朗山隧道通风风管布设的实际情况，在不干扰施工、不破坏既有风管情况下，根据风管漏风破损位置选取合适的风管断面进行测试，并尽量将测试断面选取于风管平直、风流稳定的区段。采用热敏式风速计，分别测试巴朗山隧道更换风管前后入口端和出口端漏风开孔位置的断面风速，计算得到更换风管前后不同位置的百米漏风率如图9所示。

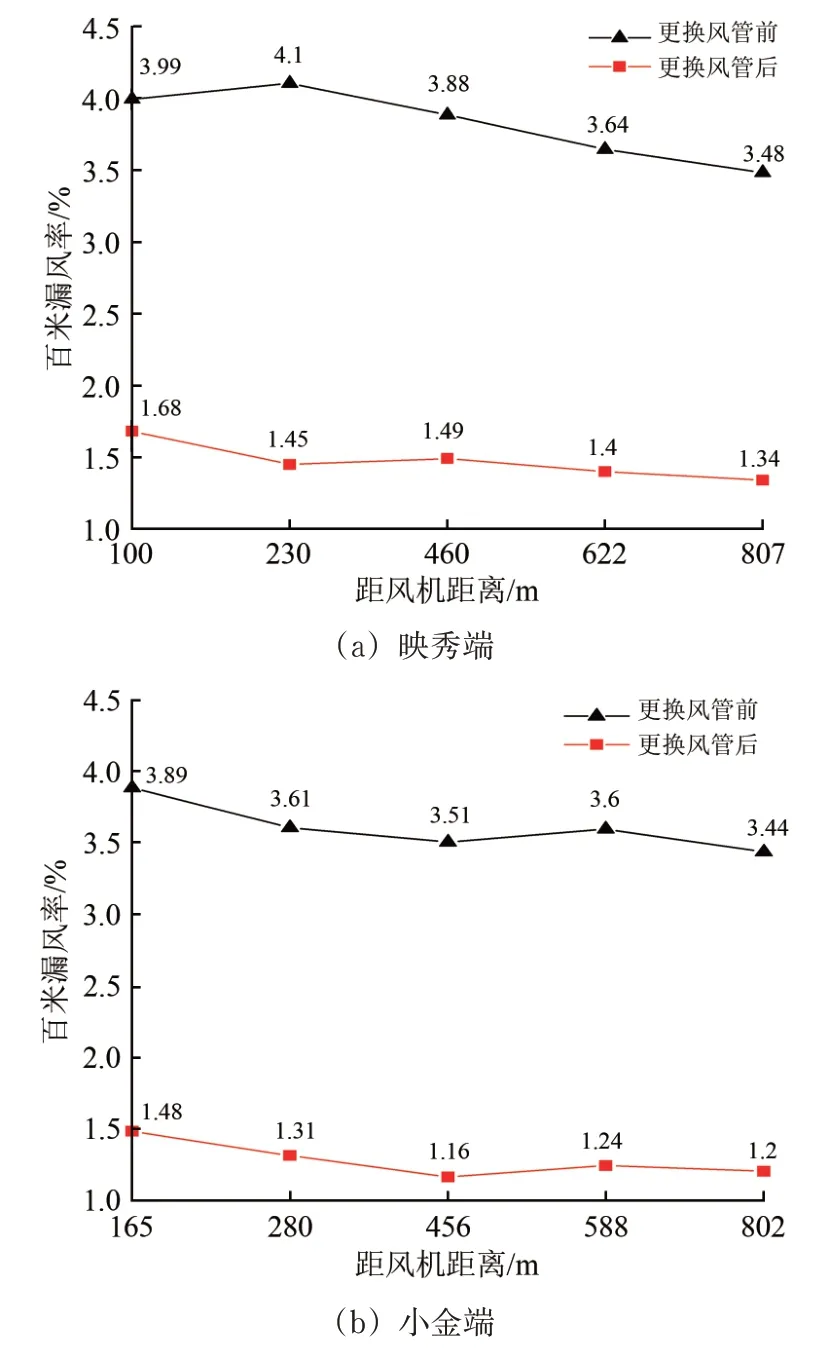
图9 出入口两端风管更换前后的百米漏风率

由图9可以看出如下结果。

（1）更换风管前，巴朗山隧道入口映秀端百米漏风率平均值为3.61%，出口小金端百米漏风率平均值为3.82%，两端平均百米漏风率均超过《公路隧道施工技术规范》所规定每百米平均漏风率不超过2%的限值［19］。测试表明，所选取测试断面漏风开孔面积过大致使风管漏风较为严重，难以满足隧道施工通风需求。

（2）更换风管后，巴朗山隧道映秀端百米漏风率平均值为1.47%，小金端百米漏风率平均值为1.28%，其数值均小于规范给定漏风率限值要求，掌子面需风量能够得到充分保障。

（3）更换风管前后，巴朗山隧道入口端平均漏风率分别从3.61%降至1.47%，出口端从3.82%降低至1.28%。

上述表明，通过更换风管减小开孔面积能够有效降低隧道风管漏风率，对高海拔隧道施工通风产生积极作用，也验证了前述理论和数值计算结论的合理性。

5 结 论

（1）基于流体力学理论和能量守恒方程，推导出的隧道单段和沿程风管漏风率计算式表明，风管漏风率η 与孔口面积A0、气体静压pj及空气密度ρ等变量相关。

（2）依托于巴朗山隧道，理论计算得到的平原和高海拔地区风管平均百米漏风率表明，高海拔地区平均百米漏风率约为平原地区的1.33倍，风管漏风率随海拔高度和漏风开孔面积的增加而升高。

（3） 结合数值模拟，得到的不同开孔面积0.04，0.06 及0.08 m2工况下风管漏风率沿程变化规律表明，高海拔平均百米漏风率亦约为平原地区的1.33 倍，风管漏风率随开孔面积增加而变幅提高。

（4）巴朗山隧道更换风管前后的漏风率现场实测结果表明，隧道入口端平均漏风率从3.61%降至1.47%，出口端从3.82%降至1.28%，更换新风管后各测试断面的漏风率相较未更换前有明显的下降，表明降低开孔面积能有效减小漏风率。