风屏障对桥上列车及桥梁气动特性影响数值模拟研究

邹思敏，何旭辉，王汉封

（1.中南大学 土木工程学院，湖南 长沙 410075；2.中南大学 高速铁路建造技术国家工程研究中心，湖南 长沙 410075）

随着高速列车速度逐步提高，列车在强风环境下的气动特性对其行车安全性和稳定性至关重要。目前，许多调查研究已表明，强风可能导致列车在运行过程中发生倾覆，甚至脱轨［1］。特别是在日本馀部桥事故调查中发现，当列车在桥上运行时，这种风险会进一步增加，因此须将列车与桥梁作为耦合系统进行研究［2］。此外，随着高速铁路网络的不断延伸，沿海地带、深切峡谷、山区垭口等强风路段越来越多，为满足列车在强风路段的安全性和稳定性，风屏障是重要的防护措施之一［3］，但伴随着风屏障的安装，列车-桥梁系统气动特性变得更为复杂。

近年来，国内外众多专家学者在风屏障对列车-桥梁系统气动特性影响方面进行了研究［4-8］。何玮等［9］研究了在风屏障透风率均为30%的情况下，不同风屏障高度（2.5，3.0，3.5 及4.0 m）对列车-桥梁系统气动特性的影响，发现风屏障对行驶在上游迎风处的列车保护作用十分明显，且随风屏障高度增加保护效果越强；王玉晶等［10］研究了高度为3.5 m、透风率为30%的风屏障对列车的影响，验证了风屏障在迎风侧的重要性；邹云峰等［11］对典型高速铁路列车与桥梁进行了风洞试验，讨论了不同风屏障高度和透风率对列车-桥梁系统气动特性的影响，发现风屏障可减小列车的平均气动力，但特征紊流的产生会使最大气动力增大；何旭辉等［12］研究了风屏障对列车气动特性的影响机理，提出了风屏障的透风率和高度需要根据具体环境进行优化；向活跃和李永乐等［13-16］基于大量风洞试验结果，采用包括数据包络分析技术（DEA）在内的多种方法评估风屏障高度在1.60~2.90 m、透风率在0~40%之间的防护效果，综合来看，当风屏障高度为2.05 m、透风率为0时，对列车的保护效果较好，当风屏障高度超过2.5 m后，其高度对列车的影响十分有限；Zhang 等［17］通过调整风屏障高度（0~5 m）和透风率（0~40%）等不同参数组合测试列车-桥梁系统的气动力系数，发现气动力系数与风屏障高度没有明显的相关性，但与风屏障透风率相关。

尽管上述研究取得了一定的成果，但均采用的是静态列车模型，没有考虑列车与桥梁/地面之间的相对运动和气动干扰，无法准确评估列车-桥梁系统的气动特性［18］。而且随着运行速度的不断提高，列车高速运动引起的列车风也成为日益重要的空气动力学问题［19-21］。因此，亟须对列车在桥上高速运行时的列车-桥梁系统气动特性展开研究，分析列车静态与移动情况下对列车-桥梁系统气动特性的影响。

本文以我国高速铁路典型列车、桥梁及风屏障为研究对象，通过数值模拟方法对列车处于静态和移动模式及有无风屏障条件下的列车-桥梁系统气动特性开展对比研究，旨在为充实和完善列车-桥梁系统气动特性评价体系提供理论和数据支撑。

1 数值仿真

以典型高速铁路32 m双线简支梁桥和CRH2型和谐号高速列车为研究对象，并采用高度为2.05 m、透风率为0 的风屏障对列车和桥梁的气动特性影响进行分析，模型尺寸和实景如图1所示。高速列车采用3 车编组模型（前车、中车及尾车），全长76.4 m（25.7+25+25.7 m）。桥梁模型的总长度为352 m，为对比有无风屏障的影响，风屏障设置于沿桥梁全长的中部。

图1 列车-桥梁系统及风屏障

建立的静态、移动列车-桥梁系统数值仿真模型如图2 所示。图中：静态列车-桥梁系统模型采用将列车静置于桥梁上的方式，2 个速度入口分别与列车车头方向垂直和平行，2 个压力出口分别与其相对，桥梁、列车及风屏障采用无滑移壁面，考虑到来流的充分发展，静态列车-桥梁系统模型设置于计算域前1/3 处；移动列车-桥梁系统模型的计算域由3个子域组成，分别为包含桥梁和风屏障的静态部分（图2（b）中绿色部分）、包含列车的移动部分（图2（b）中灰色部分）以及受横风影响流域，移动列车-桥梁系统周围的流动信息通过动、静网格之间的交界面进行传递，计算域的侧面都采用压力出口边界，速度入口与列车运动方向垂直以模拟横风来流。

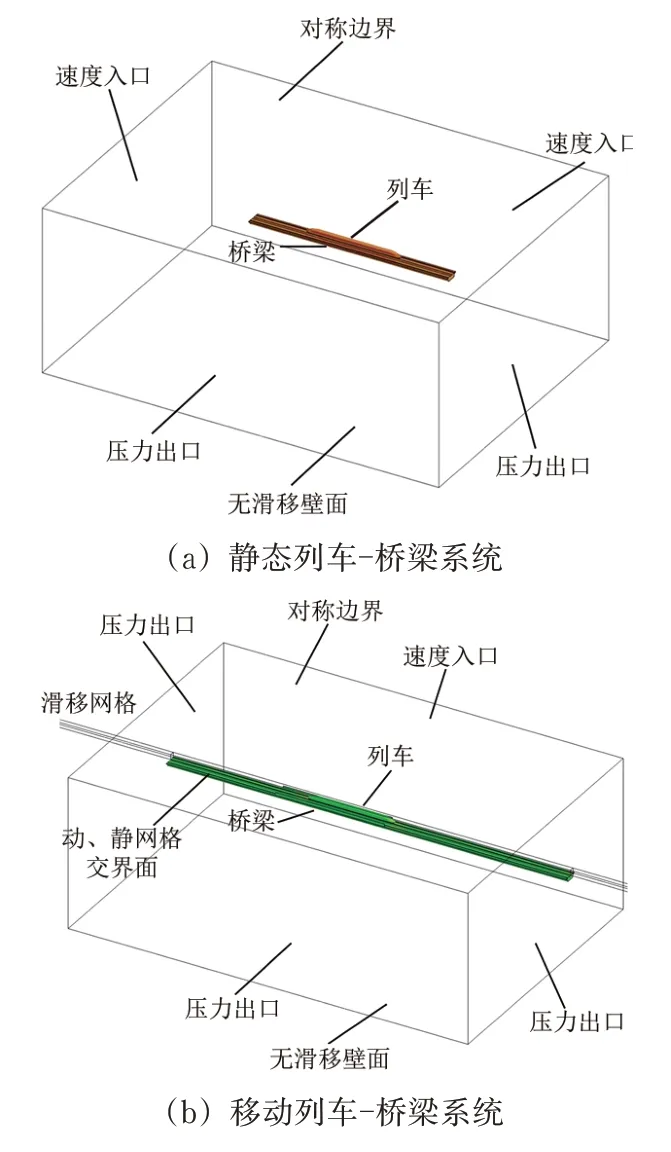
图2 数值仿真模型

为了保证数值模拟的准确性和有效性，分别对静态、移动模型的数值网格进行了多种形式划分，通过与试验结果进行对比并考虑计算效率，最终采用了最优的网格划分策略。此外，由于运行列车周围的空气流动包括横风和列车风，两者合成即为相对风速，其中横风风速为vu，与桥梁横截面垂直，列车的运行速度为v0，相对风速为vH=为进一步研究车速和风速对桥上列车和桥梁的影响，首先对静态列车-桥梁系统设置了5种模拟工况，具体设置见表1。表中：5种模拟工况分别采用了5 个不同车速和5 个横风风速；5 种模拟工况对应的合成风向角分别为8.87°，13.50°，24.20°，42.00°及90.00°。

表1 模拟工况设置

同时，为了探究桥上静态列车和移动列车模型对桥上列车和桥梁气动特性的影响规律，在移动列车-桥梁系统模型中采用了与模拟工况1 相一致的列车运行速度和横风风速。

2 静态列车模型下的气动特性

2.1 静态列车气动力

分别对静态模型设置表1 中的5 种模拟工况下的静态列车-桥梁系统进行数值模拟，获得静态列车的气动力，结果如图3所示。

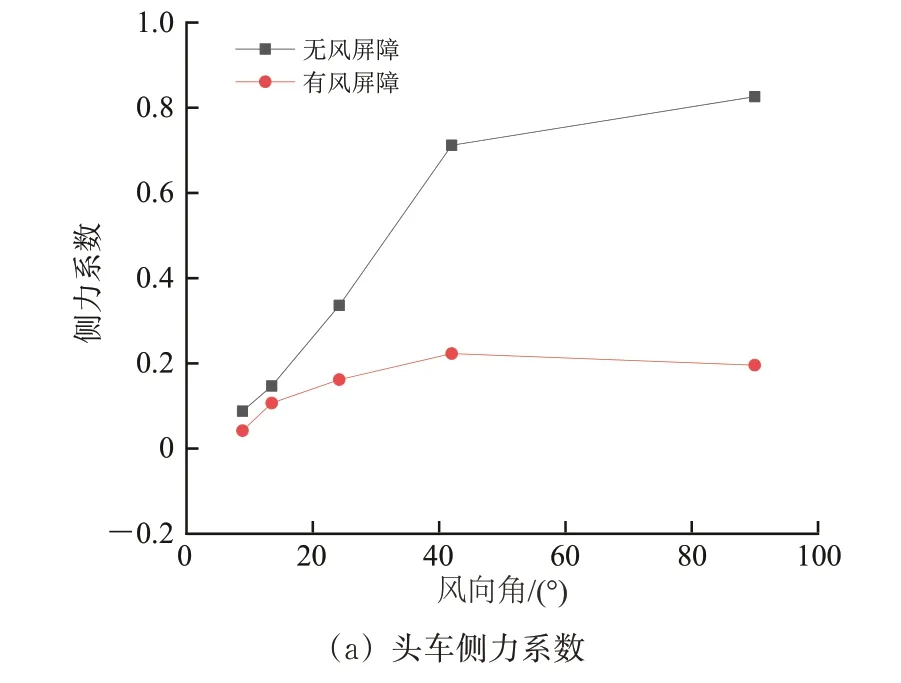
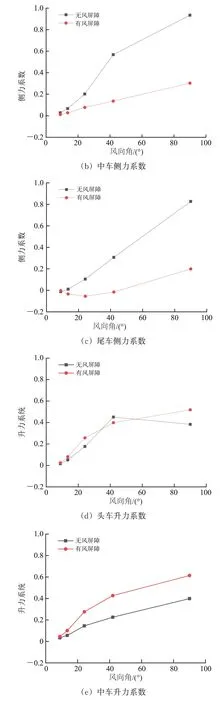
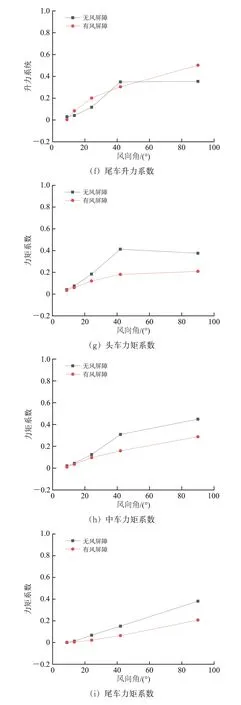
图3 不同风向角作用下列车气动力系数

由图3 可以看出：头车、中车和尾车之间的气动特性差异明显，且头车受横风影响更大；在风向角小于42°时，头车的阻力系数最大可达中车的1.5 倍，且远大于尾车；随着风向角逐渐增大，气动力系数呈阶梯式递增，较大值分布在风向角为42°～90°之间，这个规律和特征是典型从小风向角的细长体结构绕流过渡到钝体绕流的现象［22］；升力和力矩系数尽管仍呈现出随风向角增大而增大的趋势，但各节车之间的差异变得不再明显；尾车力矩系数小于头车和中车，而头车和中车力矩系数相近；风屏障大大降低了列车在横风中所承受的气动力，削弱了横风对列车的影响，特别是对头车的保护效果极为明显；而风屏障对列车的升力系数在不同工况下较为复杂，在风向角为8.87°和42°时，风屏障对头车和尾车展现出了优良的防护效果，然而在其他工况下却出现了相反的作用，总体上风屏障对列车的升力系数影响较小。

2.2 静态列车表面风压系数

沿列车车身纵向布置6 个压力分布监测截面，每个截面上设置17个压力测点，如图4所示。

图4 列车表面压力监测截面和测点分布

风压系数Cp表示为

式中：p 为列车表面风压；p0为参考大气压；ρ 为空气密度。

有、无风屏障条件下，风向角分别为90°和8.87°时的静态模型列车表面风压分布如图5 所示。图中：1#90°表示风向角为90°时1#监测截面上测得的数据；1#8.87°表示风向角为8.87°时1#监测截面上测得的数据。

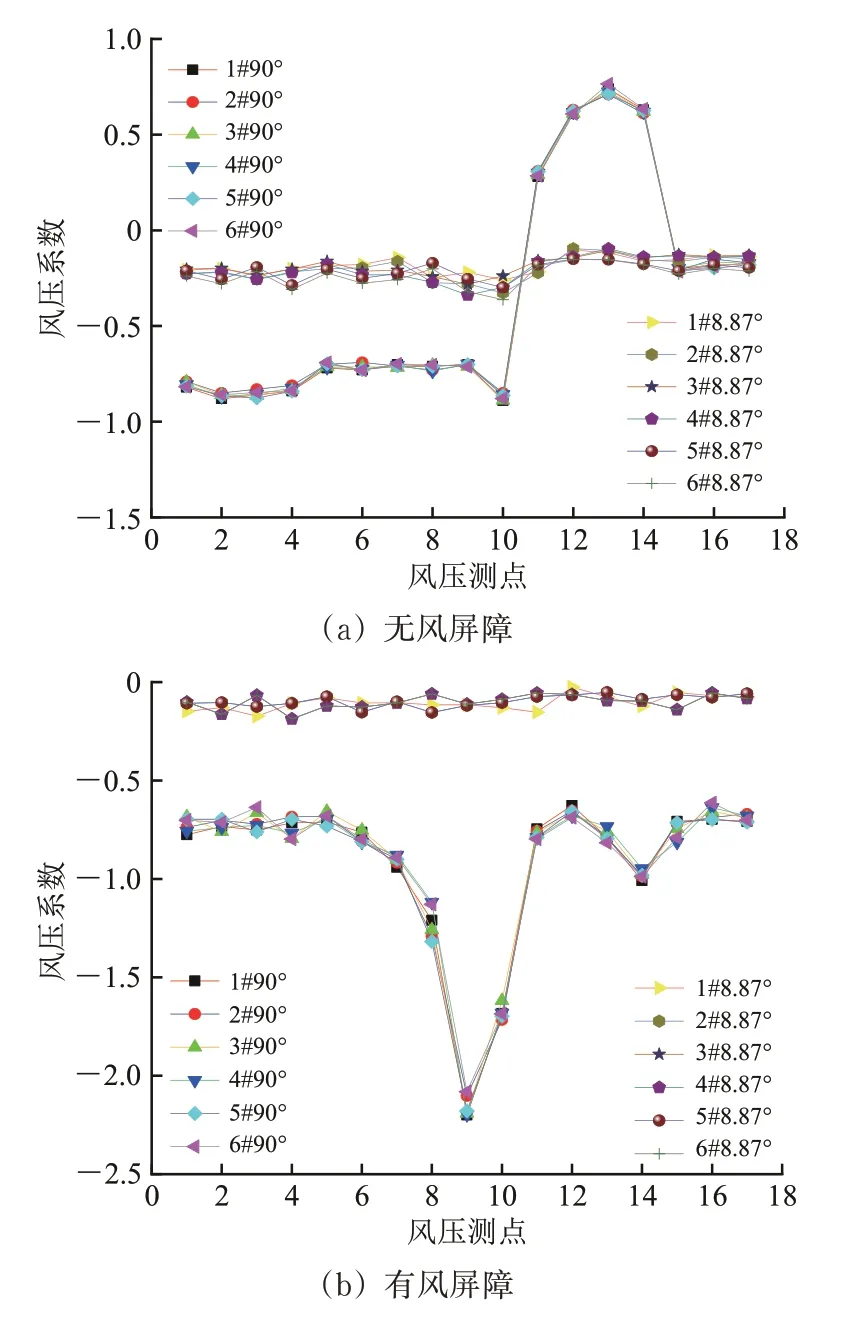
图5 静态模型下各监测截面的风压系数

由图5 可以看出：除风向角为90°时迎风面风压系数Cp值为正值外，其余风压系数均为负值；除底面外，风向角为90°时的Cp值远远大于风向角为8.87°时，这是由于列车周围的流体绕流状态从风向角为90°时的钝体过渡到8.87°时的细长体；当列车处于风向角为8.87°时，风屏障能够对列车表面风压起到降低的作用，但影响不太明显；而列车处于风向角为90°时，风屏障对列车表面风压的影响非常明显，且列车表面风压系数均为负值，这是由于风屏障的存在使列车进入了由横风通过风屏障绕流而产生的低压区；同时，无风屏障时风压负值最大位置——车肩气流分离点（测点10）在风屏障的作用下发生了偏移，转移至车肩与顶部的交接处，这是由于受到风屏障的影响，横风来流在列车表面测点9处发生分离。

可见，风向角为90°作为车-桥系统气动特性研究中最常见的风向角，可以提高对列车表面风压的评估以增加列车在横风中的安全性，但受风屏障影响时，则完全处于失真状态。

2.3 静态列车模型下的桥梁气动力

有、无风屏障时，静态列车模型下桥梁的气动力系数如图6所示。

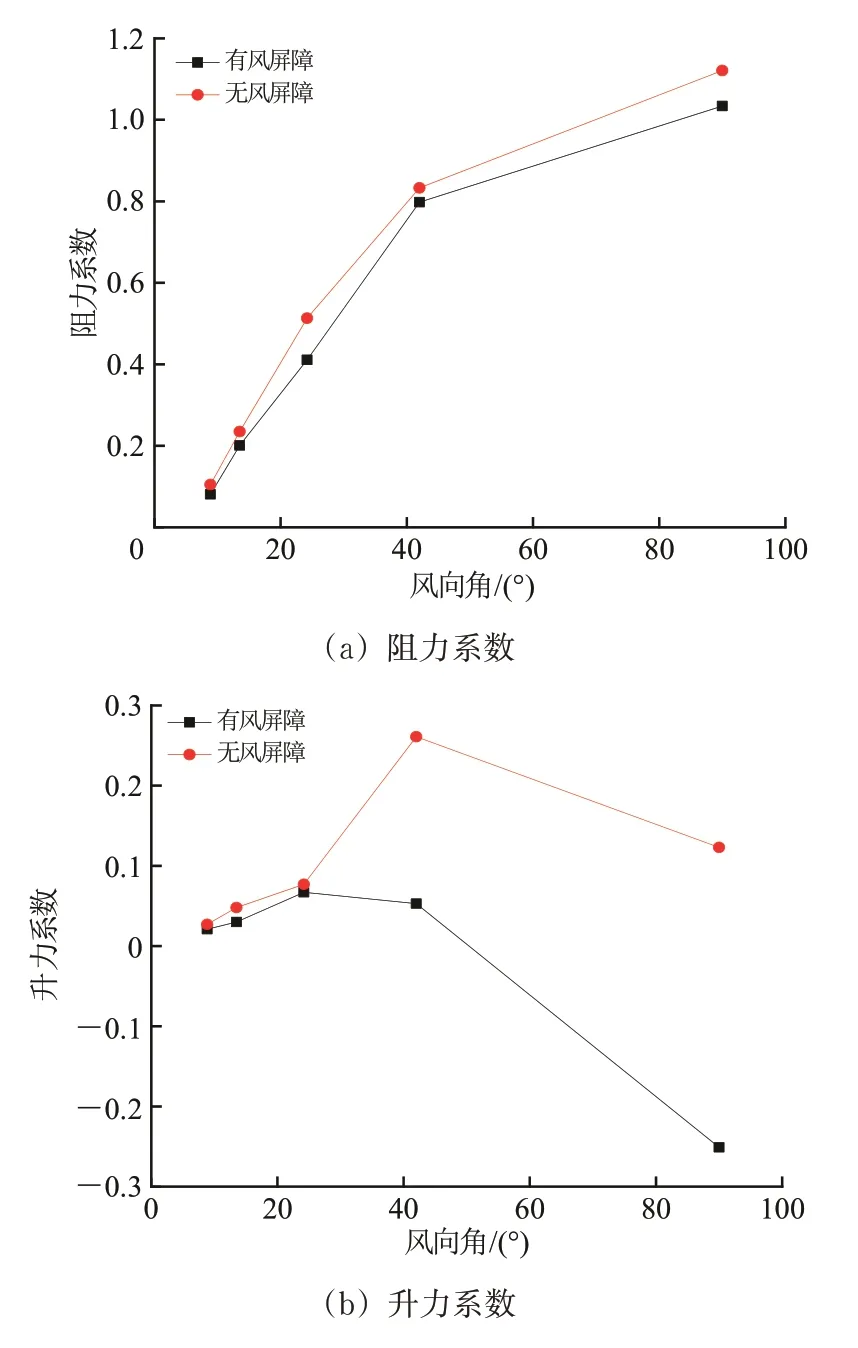
图6 有无风屏障时桥梁气动力系数对比

由图6 可以看出：桥梁的阻力系数随风向角增大而增大，风屏障会使桥梁的阻力系数降低；在风屏障的影响下，桥梁的升力系数在小风向角时变化不明显，随着风向角的增大逐渐增大；当风向角为42°与90°时，桥梁的升力系数负增长明显，这是因为在较大风向角下，横风与风屏障产生的气动绕流导致了风屏障下游形成的低压区不仅影响了列车也影响了桥梁。

3 移动列车模型下的气动特性

3.1 移动列车气动力

列车高速通过风屏障时气动力系数随时间变化曲线如图7所示。

由图7 可以看出：在列车进入风屏障前，各节车的侧力系数比较稳定，且头车的数值最大，约为0.082，中车为0.024，尾车为1个较小的负值；列车进入风屏障后，头车的侧力系数显著降低至0.01 左右，当靠近风屏障末端时，侧力系数有小的下降之后再快速恢复到之前的状态；相比之下，中车的侧力系数在有风屏障范围内的变化幅值远不如头车；尾车进入风屏障后，侧力系数变为负值且变化幅度与中车相似，这种列车侧力系数的突然下降归因于风屏障的遮挡效应；列车完全进入风屏障后，头车和中车的升力系数由较小的正值变为负值；当头车离开风屏障时，气动力系数会很快恢复到进入风屏障前的状态；尽管尾车的升力系数始终为正值，但也出现了先减小再恢复的过程；力矩系数在各节车间的变化与侧力系数和升力系数的变化相似，整体变化幅度和范围小于前两者。

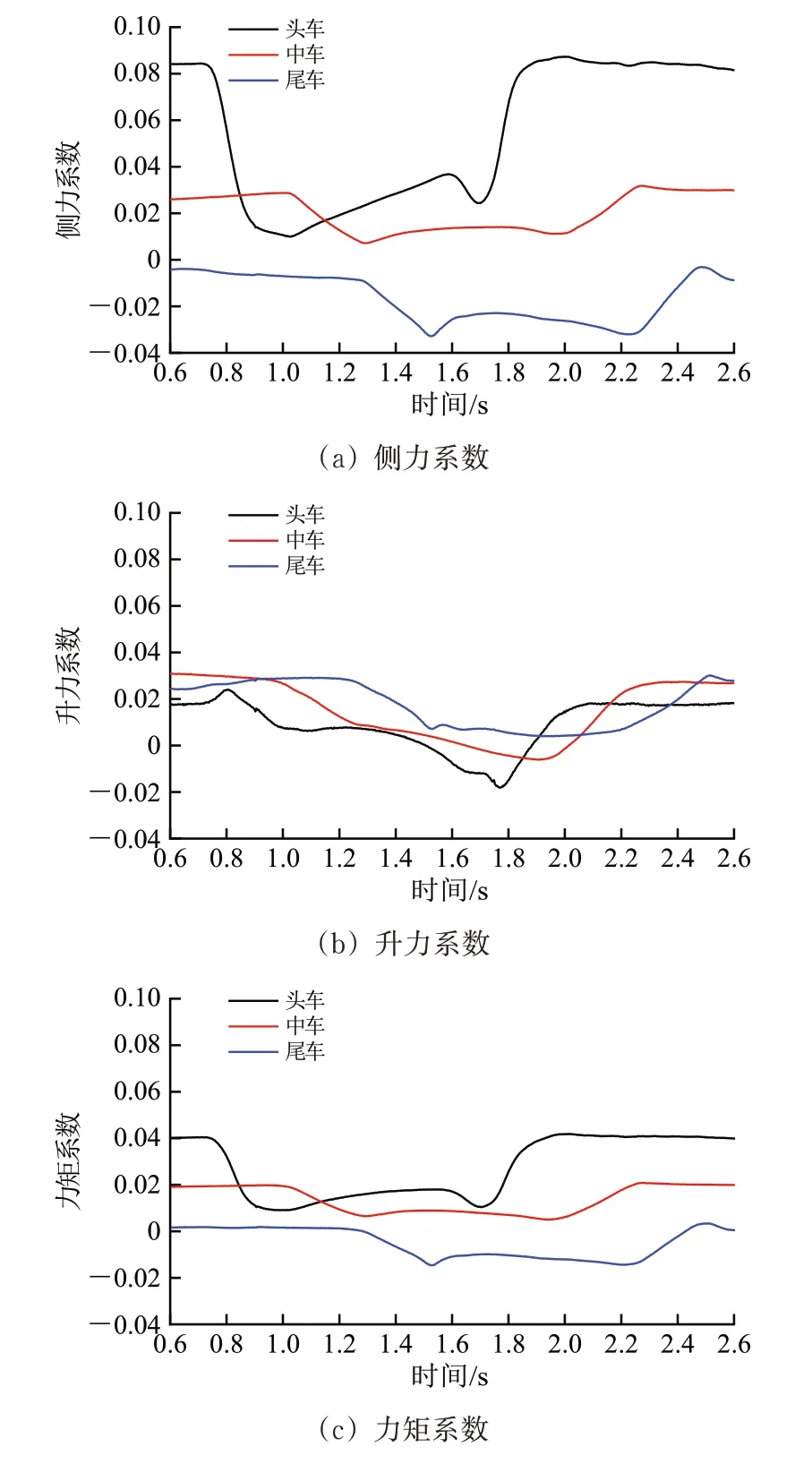
图7 移动列车气动力系数

对比图3 和图7 可以看出：在无风屏障时，静态和移动列车模型对侧力系数的影响存在相似性；然而，当列车进入风屏障时，侧力系数的变化存在差异，特别是头车和尾车差异更加明显；升力系数和力矩系数受到列车运行状态的影响也十分明显；移动列车模型下，当列车进入风屏障时，头车的升力系数由正变负；对于静态列车模型，头车升力系数均为正值。

分析结果表明，采用静态列车-桥梁系统模型对于无风屏障时的列车气动特性有相关适应性。但当有风屏障时，列车的运动对气动力有显著影响，因此，静态列车-桥梁系统模型简化的方法变得不再适用。

3.2 移动列车表面风压系数

有、无风屏障时移动列车模型各监测表面风压系数变化曲线如图8所示。

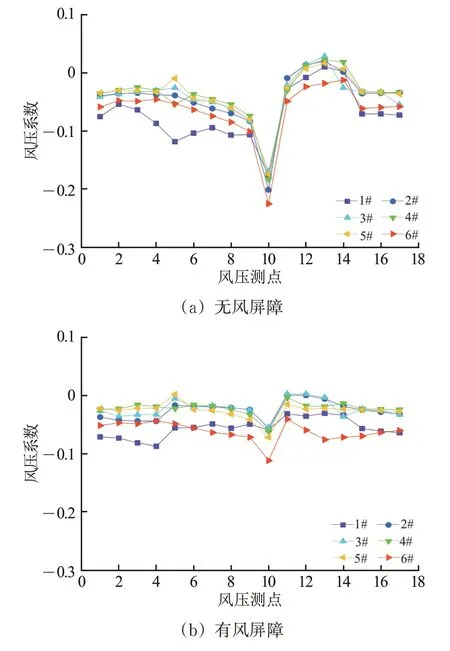
图8 移动列车模型各监测表面风压系数

由图8 可以看出：1#和6#监测截面的风压系数分布与其他截面的差异最为明显，这是由于列车头尾两端气流的强烈三维流动造成的；在无风屏障时，列车迎风面中心与列车尾部附近的风压系数为正值；位于列车车肩处附近测点10 的风压系数为负值，且绝对值最大，这是由于来流在测点10 附近发生了强烈的分离，且移动列车与桥梁间隙的流动被限制在1个很小的区域内，没有发生强烈的流动分离，列车底面没有明显的负压；在有风屏障时，列车表面风压系数与无风屏障时差异较大，迎风面上的风压系数均为负，这是由于风屏障为下游的列车提供了低压区；且列车车肩上强烈的负压消失，说明风屏障抑制了列车周围的气流分离；此外，迎风面和背风面之间的压力差相对于没有风屏障时变得不再明显。

通过对比图5 和图8 还可以发现：在相同风向角8.87°下移动列车和静态列车的风压系数分布差异明显。这表明：采用具有相同风向角的静态列车模型无法完全揭示列车在桥梁上运行时的气动特性，列车与桥梁之间的相对运动起着不可忽视的重要作用。

3.3 移动列车模型下的桥梁气动力

有、无风屏障时移动列车模型下桥梁侧力系数变化曲线如图9所示。

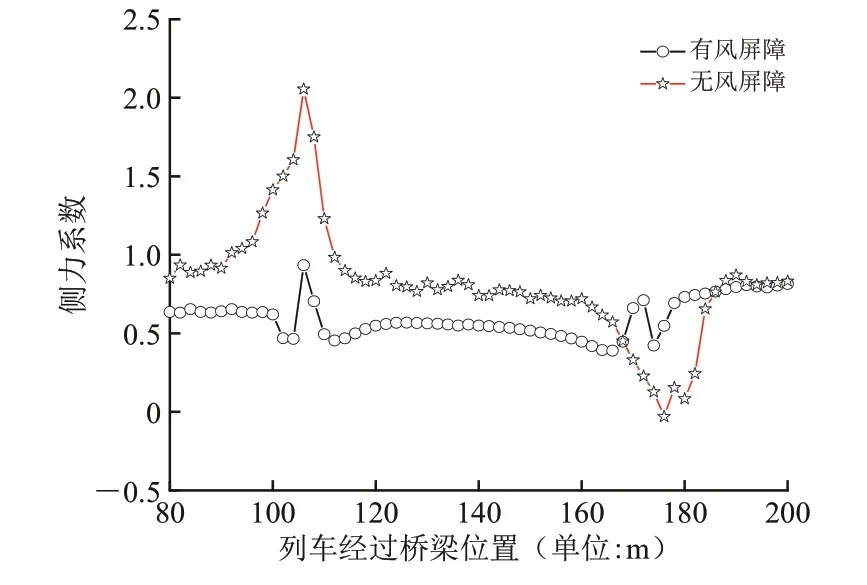
图9 桥梁侧力系数

由图9 可以看出：与上述研究列车-桥梁系统处于静态状态不同，由于列车与桥梁之间的相对运动，桥梁的侧力系数随着列车的运动发生改变，且头车的强烈气流冲击和尾车的涡旋脱落对桥梁的侧力系数影响十分明显；与图6相比，风屏障对桥梁侧力系数在静态模型中的影响是相当有限的，而在图9中，列车高速运动对桥梁侧力系数的瞬时非定常效应十分明显，且在无风屏障时，车头的影响会使桥梁的侧力系数增大1倍以上。

因此，采用静态模型计算会明显低估列车对桥梁侧力系数的影响。此外，通过图9 还可以看出，风屏障可以降低列车的高速移动和横风对桥梁的联合作用，特别是对列车的首尾效应削弱明显。

4 结 论

（1）经过对比分析不同车速和风速对应的合成风向角作用下的静态列车-桥梁系统气动特性，列车和桥梁的气动特性受风向角影响明显，总体上随风向角的增大而增大，但各节车之间的差异也十分显著，当向角小于42°时，头车的阻力系数最大可达中车的1.5 倍，且远大于尾车，头车在横风中运行风险最高，应是以后研究重点关注的对象。

（2）经过比较风屏障对列车-桥梁系统气动特性的影响规律，发现2.05 m 风屏障对列车-桥梁系统气动特性影响明显，可对桥上运行的列车起到保护作用，减小车桥系统受横风的影响，利于提高列车在桥上运行的安全性。

（3）经过对比静态和移动列车对列车-桥梁系统气动特性的影响，发现合成风向角法可以在很大程度上反映列车在上游轨道运行时的气动特性，但受风屏障影响，在特定的风向角下，静态列车与桥梁的气动力和表面风压会因风屏障而增大，因此对于静态列车和桥梁模型而言，风屏障的存在对其不利，同时也反映出该方法目前存在的困境及其不适用性。

（4）当列车在桥上运行时，受横风与列车风的叠加作用，列车和桥梁的气动特性表现出十分显著的瞬态效应，进而受风屏障的影响发生突变。显然，无论采用何种风向角，静态模型简化都无法揭示列车-桥梁系统上气动力的非定常特性。