空空导弹过失速重新定向技术研究

高昌昊，宋文萍，韩少强，路 宽，王 跃，叶 坤

（西北工业大学航空学院，陕西西安 710072）

0 引 言

空战需求的牵引和科学技术的进步，使得空空导弹成为空中对抗的主导武器。由于发射平台和攻击目标的高机动，空战态势瞬息万变，要想在战斗中取得先机，空空导弹必须具备“全向发射”能力，即载机能从不同方向对目标发动攻击。这不仅要求导弹能在较大范围内离轴发射，进而攻击载机侧前方目标；还要求导弹能在向前发射后在空中转弯，即实现“越肩发射”，进而攻击载机侧后方目标。

传统“越肩发射”主要利用导弹大攻角飞行产生的法向过载实现纯气动力转弯，受最大可用攻角限制，完成重新定向的耗时较长，且依赖发动机提供动力，能量损失大，攻击效率低。新一代空空导弹将采用提高可用攻角而不是增大升力面的方法来提高机动过载，这促使导弹升力面缩小甚至变成无翼布局，导弹的静稳定度也逐渐减小甚至趋向静不稳定，进一步提高了导弹的操纵性与机动性。同时，导弹在大攻角、超大攻角状态下的气动力具有非定常和非线性特征，舵效难以保证，这也是单纯采用气动控制面控制方式面临的难题。近年来，直接力/气动力复合控制技术的引入，极大地提高了战术导弹的机动性，通过脉冲发动机产生的推力可以快速、有效地调整导弹姿态，为实现空空导弹后向攻击时的快速重新定向提供了一种新思路。

本文研究了一种可以实现导弹快速越肩发射的过失速重新定向技术，在该机动过程中导弹经历弹射出舱、过失速翻转、重新定向几个阶段：

1）载机探测到攻击目标位于侧后，输入发射指令。

2）导弹弹射出舱，在初始弹射力等机制作用下脱离载机，并利用在大攻角、超大攻角过失速过程中出现的静不稳定性和喷流直接力使导弹姿态角翻转过一定角度，导弹姿态指向由前向迅速转为后向，在此过程中仅对导弹滚转进行控制。

3）满足点火条件后，发动机点火工作，使得导弹速度矢量逆转，在此过程中对导弹姿态进行控制，保持导引头指向稳定，完成重新定向。

过失速重新定向机动示意如图1所示，该方案无可用攻角限制，可以迅速实现导弹姿态反向和速度矢量逆转，相较于传统越肩发射方案转弯半径小、转弯时间短，能量消耗少，具有重要的研究意义。

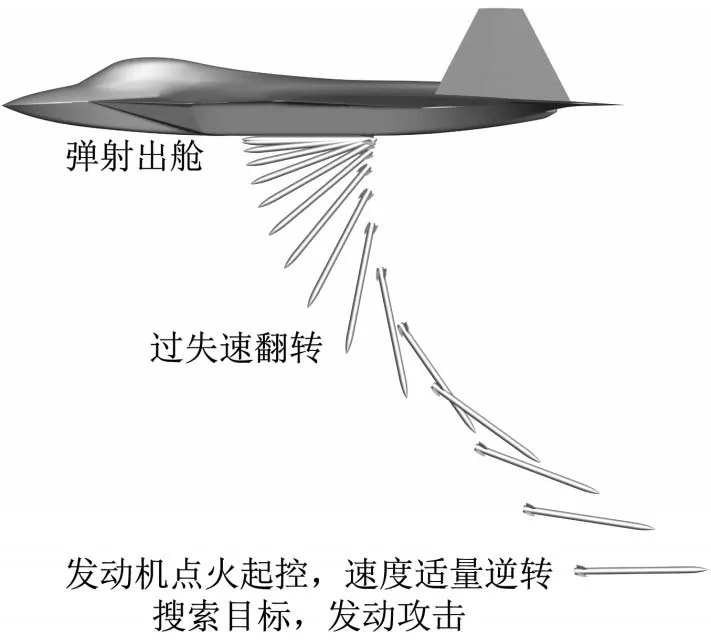
图1 过失速重新定向机动示意图Fig.1 Schematic diagram of poststall re-orientation maneuver

本文采用计算流体力学（computational fluid dynamics，CFD）耦合刚体动力学（rigid body dynamics，RBD）的数值模拟方法，结合嵌套网格技术，针对一种放宽静稳定度设计的无翼布局空空导弹，开展无载机干扰下的导弹过失速翻转过程流动数值模拟研究。针对导弹过失速翻转过程的轨迹、姿态进行定量分析，研究预置舵偏角、弹射角速度、喷流直接力控制对过失速翻转过程的影响规律，并通过预置舵偏角与直接力相结合的发射策略，使得导弹处于一种预定、可控的不稳定状态，最终实现了导弹的快速过失速重新定向（机动时间缩短至1.5 s）。

1 数值模拟方法

1.1 CFD数值方法

本文的数值模拟采用由课题组自主研发的CFD求解器，采用有限差分法进行数值离散，具备二维/三维、定常/非定常的Euler/NS方程求解能力，集成了多种空间离散格式、时间推进方法以及湍流模型，还采用当地时间步长、矩阵预处理以及多重网格法等加速收敛措施，能够在结构化多块嵌套网格上进行求解，同时该求解器具备CFD/RBD 耦合求解能力，能够实现刚体六自由度运动过程的数值模拟。

广义坐标系下忽略源项的离散形式的三维非定常N-S方程为

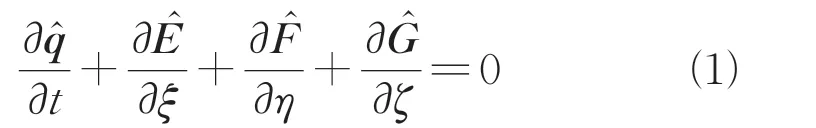
1.2 RBD数值方法

刚体六自由度运动可分解为质心的平动与刚体相对于其体轴系的转动，因此刚体动力学方程包含质心平动方程（力方程）与刚体转动方程（力矩方程）。由于体轴系下的力方程和惯性系下的力矩方程均求解困难，而高效的刚体动力学求解方法是在惯性系下求解力方程、在体轴系下求解力矩方程，最终的六自由度方程为

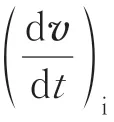
在时间步内冻结气动力（矩），采用多步Runge-Kutta法推进求解力方程与力矩方程，最终求得刚体质心位移与姿态变化。通过四元数法实现惯性系到体轴系的坐标变换，在后处理过程中转化为更加直观的欧拉角。

1.2 网格离散方法

本文采用结构化多块嵌套网格离散求解控制方程。结构化网格数据结构简单，边界层拟合能力强，流场解算精度高、效率高，但针对复杂几何外形生成高质量的结构化网格需耗费大量人力。嵌套网格方法可针对不同气动部件单独生成不同拓扑的网格，显著降低了复杂外形结构化网格的生成难度。因此，本文采用结构化多块嵌套贴体网格拟合近物面；采用多个结构化直角网格块相互嵌套组成的背景网格来离散远离物面的无黏流动区域。同时，该网格策略便于实现CFD/RBD的耦合数值模拟。

网格生成后，对网格系统进行“挖洞”与插值，即网格装配（overset grid assembly，OGA），通过“挖洞”移除“侵入”非可穿透面（non-pierced surface，NPS），如物面的网格单元，并通过插值使得相互重叠的网格块边界单元获得流场信息。

1.3 数值方法验证

针对一种长细比为20 的无翼布局空空导弹，在=0°～180°的攻角范围内对其非定常气动特性进行评估，对计算方法和求解程序进行精度验证。

采用结构化多块嵌套网格，贴体网格总量约530万，共17块，壁面第一层网格高度约1×10m（保持壁面+为1的量级），背景网格总量约420万，总网格量约950万，网格示意如图2所示。

图2 细长体导弹网格示意图Fig.2 Grids diagram of slender missile

计算状态为：=0.8、=2.0×10、=0°～180°。

由于导弹在大攻角状态下流场具有明显的非定常特征，因此在定攻角状态下，采用非定常计算方法，可以模拟出更加真实的流场和更加精确的气动力，时间步长取自由来流流过弹体最大直径的三十分之一。0°～180°攻角下导弹相对于弹理论尖点的力（矩）系数随攻角变化曲线如图3所示，数值模拟结果与试验值相较的最大误差不超过10%，验证了所采用的CFD数值方法及计算程序具备大攻角过失速气动特性的计算能力。

图3 法向力、俯仰力矩系数与试验值的比较Fig.3 Force&pitch moment coefficient compared with experimental values

采用多体分离标模——WPFS（wing/pylon/finned store）模型的分离投放算例，验证本求解器的CFD/RBD耦合求解能力。

贴体网格总量约500万，共15块，壁面第一层网格高度约1×10m（保持壁面+为1的量级），背景网格总量700万，总网格量约1 200万，网格示意如图4所示。

图4 WPFS网格示意图Fig.4 Grids diagram of WPFS

前0.3 s外挂物质心位移轨迹与姿态角变化如图5所示，数值模拟结果与试验值吻合良好，验证了求解器的CFD/RBD耦合求解方法的准确性。

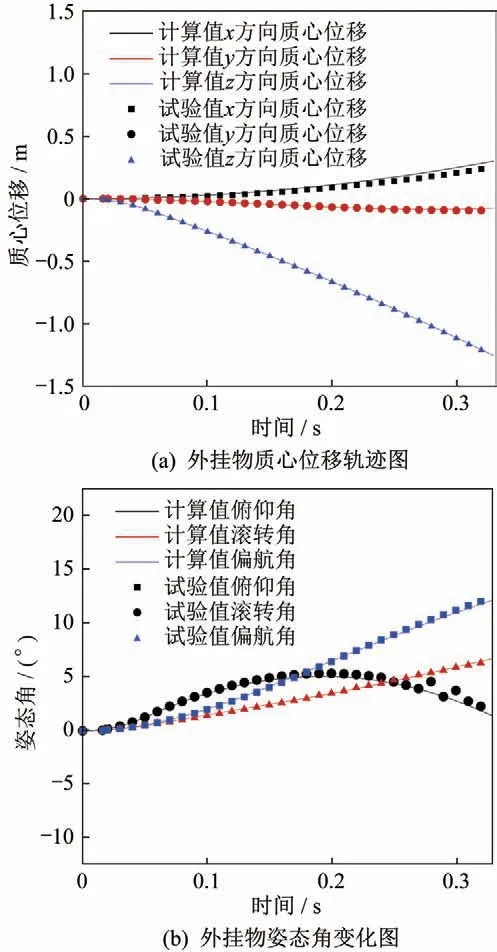
图5 外挂物下落轨迹及姿态变化与试验值的对比Fig.5 Comparison of computed kinetic characteristics of store during separation and experimental data

2 无载机干扰的导弹过失速重新定向特性研究

采用1.3.1节中进行大攻角气动特性评估的无翼布局细长体导弹，对无载机干扰的导弹过失速翻转特性进行研究，计算状态：=0.8、=2.0×10、=0°。

导弹的无量纲几何参数如表1所示。

表1 导弹无量纲几何参数Tab.1 Non-dimensional geometric parameters of the missile

采用1.3.2 节的网格，使用背景网格自适应加密，如图6所示，以确保在导弹六自由度运动过程中重叠区域的插值及贡献单元在尺度上是匹配的。空间离散采用二阶Roe迎风格式，时间离散采用二阶Euler隐格式，时间步长为0.001 s，内迭代30步，湍流模型选用S-A一方程模型。

图6 背景网格自适应加密Fig.6 Background grids adaptive refine

2.1 导弹姿态指向逆转过程的稳定性变化

对无任何措施影响下的导弹自由下落过程开展数值模拟，所有舵面预置舵偏=0°，弹射角速度=0（°）/s。导弹自由下落1 s 内的质心位移与姿态角变化以及下落轨迹如图7所示，由图可知，在无任何翻转策略介入时，导弹仅有略微的低头趋势。

图7 无任何干扰时导弹自由下落示意图（1 s内）Fig.7 Kinetic characteristics of slender missile during drop without interference（within 1 s）

有/无预置舵偏时导弹相对于质心的俯仰力矩系数随攻角变化曲线如图8所示，结合图中斜率可知，导弹气动中心随攻角变化而变化，即稳定性会随攻角变化而变化，总体而言，有/无预置舵偏情况下的稳定性随攻角变化趋势基本一致：

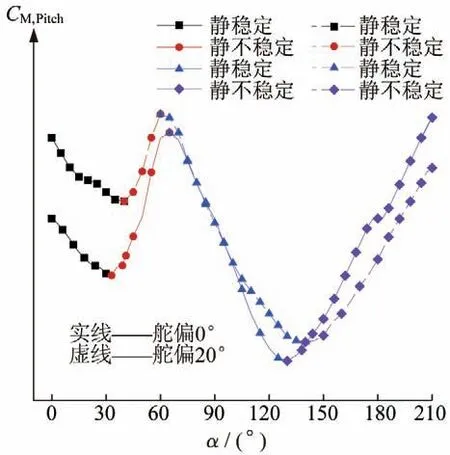
图8 导弹相对于质心的俯仰力矩系数随攻角变化曲线Fig.8 Pitching moment coefficient of slender missile relative to centroid varies with the angle of attack

1）当翻转角≤30°时，俯仰力矩系数斜率为负，导弹静稳定，仅仅依靠其自身的静态气动特性，无法实现过失速翻转，因而需利用其他发射策略为导弹提供初始低头俯仰力矩；

2）当30°＜≤65°时，尾舵气动力使得气动中心前移，俯仰力矩系数斜率变为正，导弹变为静不稳定，此时翻转幅度会随着翻转角的增大而增大；

3）当65°＜≤130°时，舵面当地攻角过大，舵面失速而导致其失效，如图8所示，此时有/无舵偏的导弹俯仰力矩几乎一致，其稳定性主要依赖弹身气动力，导弹恢复静稳定，若其惯性无法克服静稳定性，则无法完成过失速翻转；

4）当130°＜≤180°时，尾翼朝前，舵面恢复舵效，该姿态下可以将导弹等效为钝头“鸭式布局”，气动中心位于质心之前，导弹再次变为静不稳定；

5）当＞180°时，其稳定性与130°＜≤180°的情况类似，此时导弹翻转特性是发散的，因此当导弹翻转至180°时，需进行末端控制，使得导弹姿态稳定在该状态，保持导引头指向稳定，完成重新定向。

由于初始阶段导弹静稳定，仅依靠其自身静态气动特性，无法实现过失速翻转，因此需要引入增强其过失速翻转能力的措施，在后续章节中将研究不同措施对导弹过失速翻转特性的影响。

2.2 不同因素对导弹过失速翻转特性的影响研究

针对不同预置舵偏下导弹的翻转特性进行研究，单个舵面预置舵偏分别为5°、10°、15°、20°、25°、30°（定义舵面后缘向下为正偏），数值模拟中不考虑舵面偏转引起的转动惯量变化，预置正舵偏使得尾舵在无来流攻角时有了一定的当地攻角，产生法向力，进而使得导弹产生初始低头力矩，使其克服俯仰角较小时的静稳定性，开始向下翻转。不同预置舵偏下导弹的俯仰角变化曲线及翻转下落轨迹如图9和图10所示，随着预置舵偏增大，导弹翻转幅度增大，但无法克服图8中蓝线对应的静稳定段。如图10（h）所示，预置30°舵偏角，导弹在1.4 s 时最多可翻转至160°，随后，翻转幅度逐渐减小。单纯依靠增大预置舵偏角无法实现0°～180°的姿态指向逆转，由于舵面干涉，预置舵偏角不能无上限增大，同时在过失速翻转过程中尾舵需预留滚动舵偏以控制滚转姿态，因此预置舵偏不宜过大。在后续章节的研究中预置舵偏角最大不超过20°，并研究其他措施对导弹过失速翻转特性的影响。

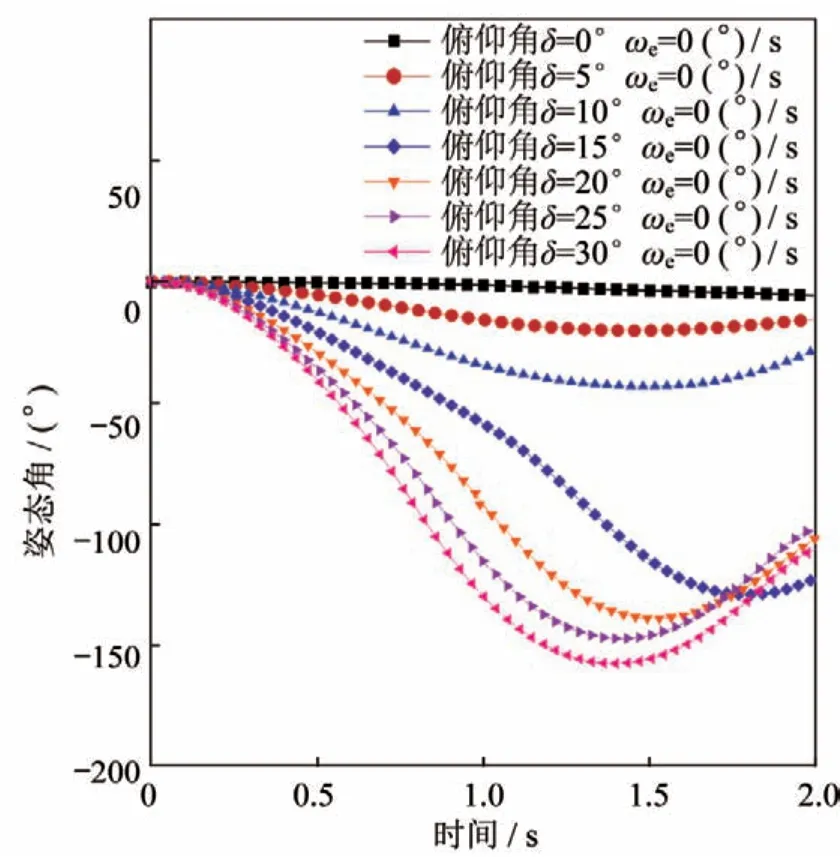
图9 不同预置舵偏下导弹俯仰角变化曲线Fig.9 Pitch angles under different preset rudder deflection

图10 不同预置舵偏下导弹翻转下落轨迹示意图Fig.10 Trajectories during drop under different preset rudder deflection

对不同弹射角速度下导弹的过失速翻转特性进行研究，单个舵面预置舵偏=15°，弹射角速度分别为10（°）/s、20（°）/s、30（°）/s、40（°）/s。不同弹射角速度下导弹俯仰角变化曲线如图11所示，由图可知，随着弹射角速度增大，导弹过失速翻转的最大幅度没有改善（如图12所示），仍无法克服图8中蓝线对应的静稳定段。同时，较大的弹射角速度要求发射架提供较大的角动量，对载机及弹射装置强度提出了较高要求，增加了结构设计难度。因此，在后文的研究中不再考虑弹射角速度的影响。

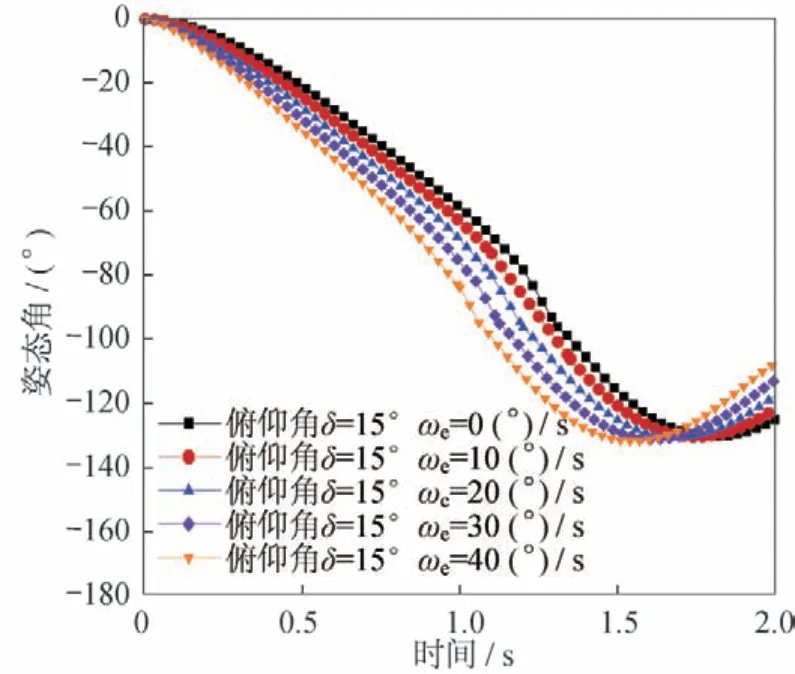
图11 不同弹射角速度下导弹俯仰角变化曲线Fig.11 Pitch angles under different ejection angular velocities

图12 20°预置舵偏角时不同直接力介入时间下导弹俯仰角变化曲线Fig.12 Pitch angles under different direct force control time（δ=20°）

根据前文，单纯依靠预置舵偏与弹射角速度难以实现导弹0°～180°姿态指向逆转，如图9所示，单个舵面最大30°预置舵偏下导弹在1.4 s 时最多可翻转至160°，随后翻转角逐渐减小。本节中，尝试在过失速翻转末端引入短暂的喷流直接力，以克服静稳定翻转段，实现180°的姿态指向逆转。

设置直接力模型，直接力喷口相对弹头距离=22.33%，直接力能使导弹产生0.7的瞬时法向过载。预置舵偏角=20°，弹射角速度=0（°）/s。

无直接力作用时导弹的翻转角随时间变化曲线如图9所示，已知导弹翻转特性会随其稳定性变化而变化，分别在图8中红线对应的静不稳定段（0.37～0.81 s）与蓝线对应的静稳定段（0.81～1.1 s）内，介入作用时间为0.1 s的直接力，研究直接力对导弹过失速翻转特性影响。图13展示了不同时刻介入直接力下导弹过失速翻转角随时间变化曲线，由图可知，在红线对应的静不稳定段内介入直接力，无法实现180°的姿态指向逆转；而在蓝线对应的静稳定段内介入直接力，可以有效地增大导弹翻转幅度。在静稳定段内，适当调整直接力介入时机、作用时间和大小，最终可以实现180°的姿态指向逆转。

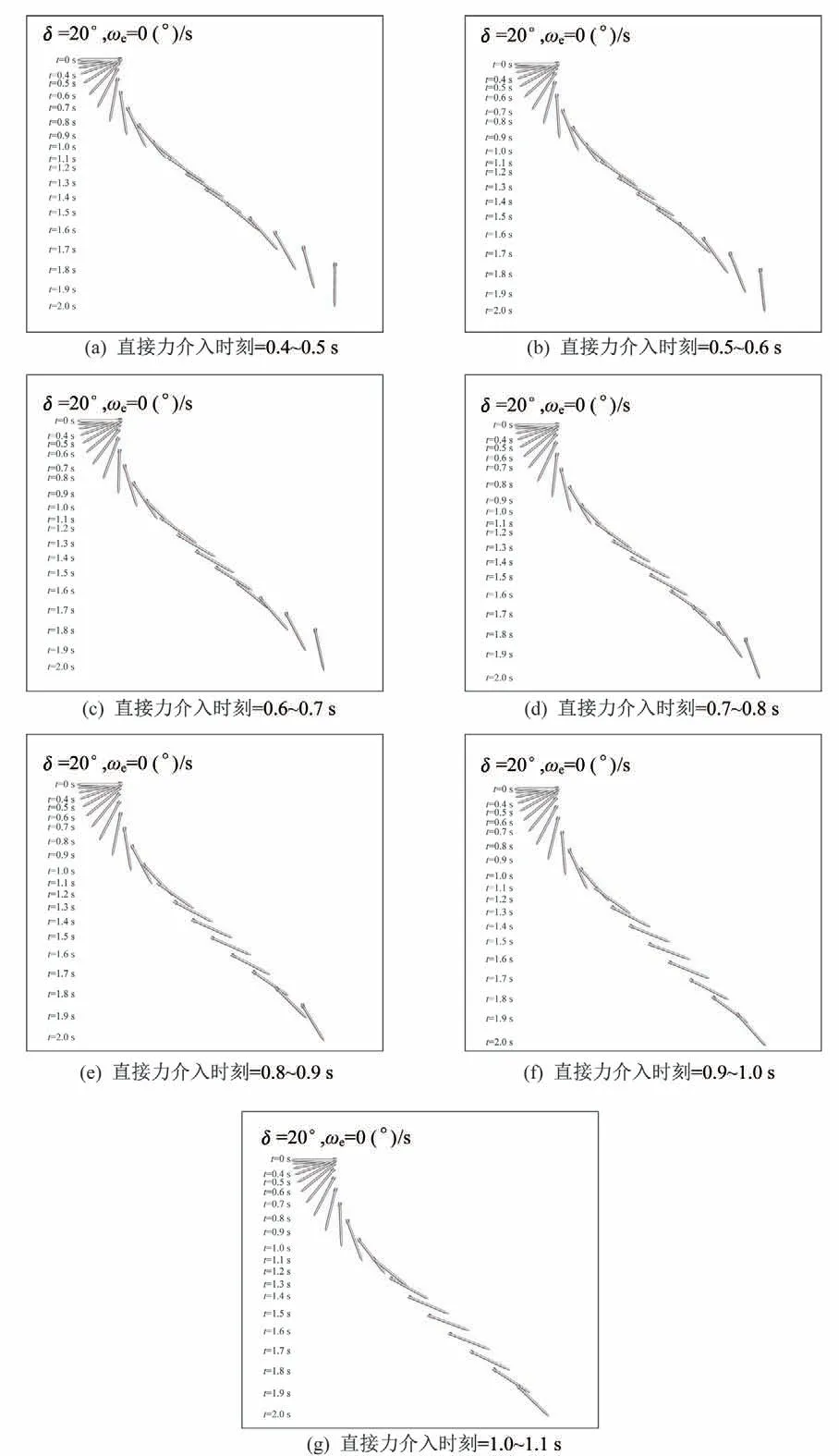
图13 不同直接力介入时间下导弹翻转轨迹Fig.13 Trajectories during drop under direct force control times

2.3 预置舵偏与喷流直接力相结合的导弹过失速翻转策略

根据上文对预置舵偏、弹射角速度、直接力对导弹翻转特性的影响分析，可得到如下预置舵偏与喷流直接力相结合的导弹过失速翻转策略：预置舵偏角=20°，弹射角速度=0（°）/s，将作用时间延长至0.2 s，并在0.8～1.0 s介入，即可实现导弹快速姿态反向。

导弹的翻转轨迹与姿态随时间变化如图14所示，由图可知，导弹最终在1.5 s 时实现了180°的指向逆转，证明了采用预置舵偏+合适的喷流直接力辅助实现空空导弹的快速过失速重新定向机动的可行性。图15给出了导弹过失速翻转角超过90°时的流线及涡量示意图，此时弹身背风面流动类似于卡门涡街流动，流动的非对称效应不明显，因而导弹的滚转与偏航幅度较小，横航向稳定性较好。但在翻转至180°之后，弹尾迎风，由于预置舵偏使得导弹产生了抬头力矩，导弹会进一步抬头。图16给出了导弹完成姿态指向逆转时刻的流线及涡量示意图，由图可知，在非定常效应下，导弹附近会出现非对称分离涡，使得导弹横航不再稳定，滚转存在发散趋势，因而在过失速翻转末端，应及时摆正舵面，并通过控制系统稳定导弹姿态，保持导引头指向稳定，完成重新定向。

图14 直接力介入时刻0.8～1.0 s时导弹翻转轨迹示意图Fig.14 Kinetic trajectory of slender missile when the direct force control time is 0.8～1.0 s

图15 翻转角超过90°时的流线及涡量示意图Fig.15 Streamlines and vorticity magnitude contour when pitch angle exceeds 90°

图16 翻转角超过180°时的流线及涡量示意图Fig.16 Streamlines and vorticity magnitude contour when pitch angle exceeds 180°

3 结束语

本文基于课题组自主研发的CFD 求解器，进行了无载机干扰下导弹六自由度下落的数值模拟。结果表明导弹过失速翻转过程中的稳定性会随攻角变化而变化，由于初始状态的静稳定性，若不施加任何措施，导弹无法自动翻转，因此必须施加合适的翻转策略。重点研究了预置舵偏、弹射角速度与直接力对导弹翻转特性的影响规律，利用预置舵偏并在适当的直接力辅助下，实现了导弹的快速过失速翻转，在1.5 s内完成了180°的姿态指向逆转，证明了过失速重新定向技术的可行性。

由于本研究尚未考虑载机干扰，下一步拟开展载机干扰对空空导弹过失速重新定向过程的影响研究，以推进过失速重新定向技术及策略的工程应用。