鸭式布局旋转导弹舵翼干扰问题气动特性研究
彭中良,陆 韵,周志超,黄 臻,刘泰涞
(上海机电工程研究所,上海 201109)
0 引 言
旋转导弹是指在飞行过程中绕其纵轴自旋的一类导弹,气动布局一般采用鸭式布局。目前典型的鸭式布局导弹有Stinger系列、RAM系列等。鸭式布局的主要气动特点是鸭舵洗流对尾翼产生副翼反效作用,鸭舵引起的洗流一般属远区洗流,从前翼(舵)后缘拖出的自由涡已经形成集中涡,非对称下洗流场对尾翼产生反向诱导滚转力矩,这种旋转力矩随着布局形式、马赫数以及攻角的变化不同而对导弹转速产生不同影响。导弹旋转影响各部件表面的边界层状态,改变了边界层分离点,从而使涡迹发生偏转,进而改变流场的状态。这些变化将直接影响导弹的气动特性,特别是主要由流动分离产生的马格努斯效应造成的附加侧向力和力矩。因此,舵翼干扰问题是鸭式布局导弹的基本问题。
美军方、NASA以及Raytheon公司在20世纪八九十年代围绕旋转导弹的气动特性开展研究,包括风洞旋转测力试验的系列试验、更高精度的瞬态测力试验以及大量动态流场和气动特性的CFD计算。国内80年代开始对旋转导弹气动特性进行了系统研究。近年来,李小林等开展了短边条对舵面影响研究,伍彬等开展了不同鸭舵外形对旋转导弹尾翼压力分布影响的气动特性研究,得到不同鸭舵外形对尾翼上非定常压力系数及气动力变化规律,结果表明降低旋涡干扰需从旋涡强度与旋涡影响位置结合选择。徐科杰等对低速旋转导弹的滚转特性进行数值模拟研究,提出了小斜置角、低转速情况下滚转力矩及平衡转速的经验公式。
本文采用全弹旋转风洞试验,对舵翼干扰问题带来的导弹气动特性变化进行研究,得到不同的舵翼周向角对导弹的旋转稳定性有较大的影响,为优化导弹的气动布局、提高旋转和飞行稳定性提供设计依据。
1 无量纲速度转化及数据处理
本次试验测得风洞来流条件下的转速,通过无量纲转化,得到了在实际空中飞行时的转速,本文分析采用的转速均为实际空中转速。保持天地转速一致的无量纲转化公式如式(1)所示,满足该公式也意味着相同舵翼周向角下洗流的影响规律保持一致。

式中:ω、、分别为实际飞行中导弹的转速、长度、飞行速度;ω、、为风洞中导弹的转速、长度、速度。
马格努斯系数由旋转状态下的侧向力系数和偏航力矩系数分别减去对应马赫数和攻角下的静态平均气动系数(滚转角=0和=90两点平均)获得。图1为本次试验测得的纹影图。

图1 旋转吹风纹影图(左:攻角a=0°;右:a=8°)Fig.1 Schlieren photo of wind-tunnel rotating experiment
2 不同舵翼周向角下的转速分析
图2为不同舵翼周向角下转速随攻角变化的曲线,可以看出:在小攻角条件时(1°~3°),转速波动比较大;在攻角4°~10°范围内,转速逐渐减小,变化比较平稳。=2 时,由舵翼周向角引起的转速变化基本不超过2 r/s,在舵翼周向角34.4°~54.4°范围内,转速变化稍大于舵翼周向角4.4°~34.4°。=2.5 和=1.8 时的转速波动略大,最大波动达到5 r/s 左右,但是在所有试验中均未出现转速凹坑现象。
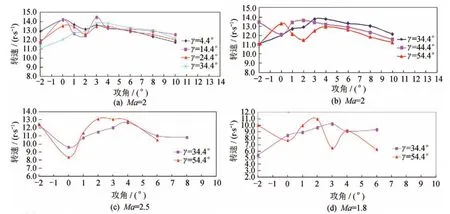
图2 不同舵翼周向角转速随攻角变化曲线Fig.2 Rolling rate vs.attack angle of different canard-wing setting angle
3 纵向气动特性分析
图3为不同舵翼周向安装角法向力系数随攻角变化曲线,从计算结果看,采用四点、八点平均获得的法向力系数与旋转情况下测得的平均法向力系数基本一致;不同舵翼周向安装角下的法向力系数也基本相同。图4为法向力系数随转速变化情况。

图3 不同舵翼周向安装角法向力系数随攻角变化曲线Fig.3 Normal force coefficient vs.attack angle of different canard-wing setting angle
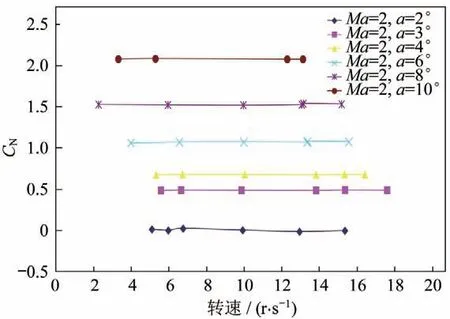
图4 法向力系数随转速变化情况Fig.4 Normal force coefficient vs.rolling rate
将不同舵翼周向安装角的纵向压心系数进行比较,实验结果见图5,从中可以看出,采用45°舵翼周向安装角得到的八点平均压心系数,与34.4°舵翼周向安装角得到的系数相比,相差不超过0.5%,采用四点平均方法也可以得到令人满意的结果。
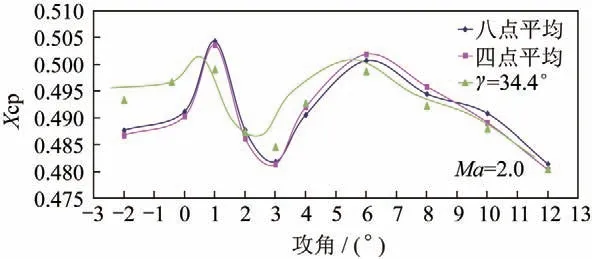
图5 不同舵翼周向安装角压心系数比较Fig.5 Pressure center coefficient under different canard-wing setting angle
从图6可以看出,在攻角1°~3°情况下,不同舵翼周向角下的压心系数有所差别。图6(a)中有最大相差(在1.5%以内),当攻角达到6°以后,不同舵翼周向角的压心系数差别都下降到约0.3%以内。除了舵翼周向角4.4°和54.4°,在其他舵翼周向角下,1°攻角时的压心相对靠后,3°攻角时的压心相对靠前。当攻角达到6°时,压心相对靠后,随着攻角的进一步增大,压心又前移。图6(a)中舵翼周向角为4.4°时,在攻角1°到3°之间的压心变化与上述其他周向角的变化趋势相反;舵翼周向角为54.4°时的压心系数变化最为平缓。采用四点或八点平均获得的压心系数在1°到3°攻角下的变化幅度比旋转情况下来得大。上述这种变化可能是当舵翼周向角不同时,鸭舵对尾翼的洗流影响不一样造成的,而这种洗流影响在小攻角范围(1°~3°)内影响较大,随着攻角的增大,影响逐渐变小。
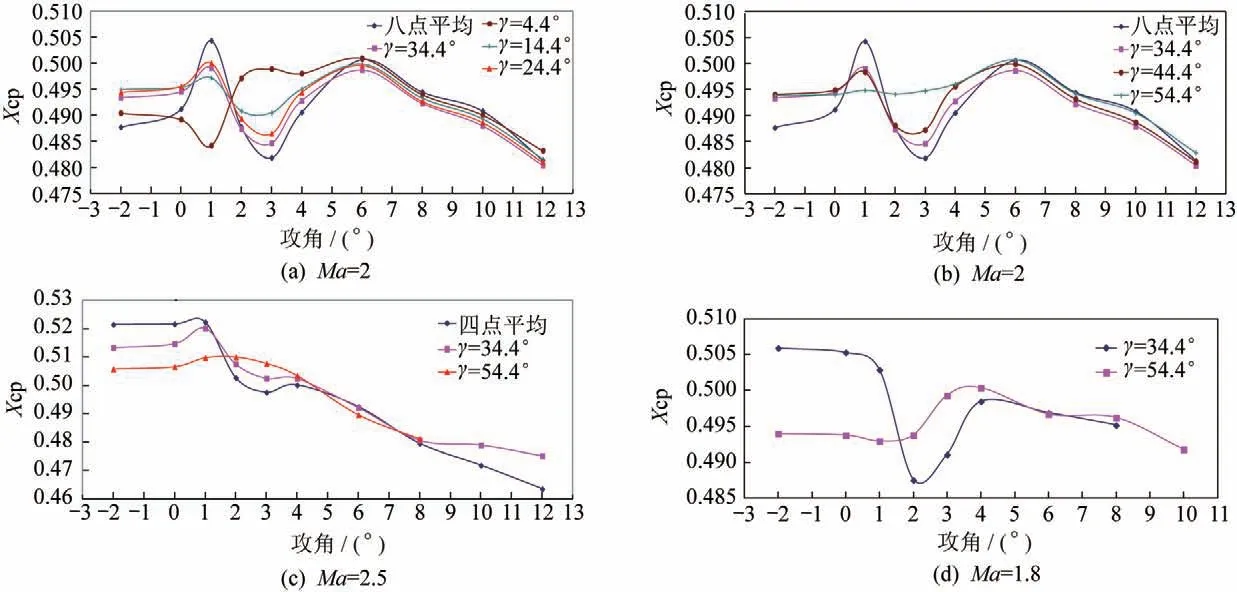
图6 不同舵翼周向安装角压心系数随攻角变化曲线Fig.6 Pressure center coefficient vs.attack angle of different canard-wing setting angle
图7为压心系数随转速变化曲线。可以看出,攻角相同时,压心系数随转速的变化在0.4%以内,变化不大。上述结果表明:在讨论旋转弹纵向气动问题时,可采用准定常方法。

图7 压心系数随转速变化曲线Fig.7 Pressure center coefficient vs.rolling rate
4 马格努斯效应分析
将试验得到的随攻角变化的马格努斯力系数与力矩系数和其他试验结果综合比较。由图8和图9可以看出,在小攻角(<6°)时,马格努斯力和力矩系数均不大;在=6°左右,侧向气动力系数发生突变,此后随攻角增大振荡加剧。

图8 随攻角变化马格努斯力系数比较Fig.8 Magnus force coefficient vs.angle of attack

图9 随攻角变化的马格努斯力矩系数比较Fig.9 Magnus moment coefficient vs.angle of attack
本次试验获得的马格努斯效应(包括马格努斯力系数和力矩系数)随转速变化波动较大,非线性较强。从量级上看,=2 时,马格努斯力系数最大可到法向力系数的10%,马格努斯力矩系数最大约为俯仰力矩系数的10%。当转速在10~12 r/s 时,小攻角下的马格努斯力和力矩系数相对较小(见图10~13)。马格努斯力系数与法向力系数的比值随着攻角的增大由正变负;马格努斯力矩系数与俯仰力矩系数的比值,随着攻角的增大由负变正(见图14~15)。

图10 马格努斯力系数Fig.10 Magnus force coefficient

图14 马格努斯力/法向力Fig.14 Magnus force/normal force
对阻力特性进行分析,由图16和图17可以看出,四点平均和八点平均获得的阻力与滚转条件下的阻力趋势一致,大小基本相同,在小攻角时略大,大攻角时略小;不同舵翼周向角下的阻力系数差别在1%以内。转速变化造成的阻力系数变化在2%以内。

图11 对头部顶点马格努斯力矩系数Fig.11 Magnus moment coefficientof head

图12 对满载质心马格努斯力矩系数Fig.12 Magnus moment coefficient of full-load centroid

图13 对空载质心马格努斯力矩系数Fig.13 Magnus moment coefficient of no-load centroid
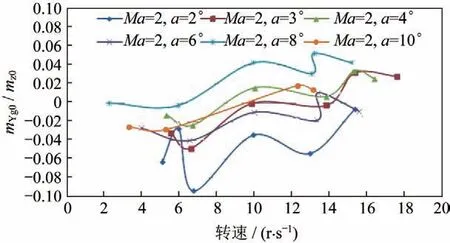
图15 马格努斯力矩系数/俯仰力矩系数Fig.15 Magnus moment coefficient/pitching moment

图16 阻力系数随攻角变化曲线Fig.16 Drag coefficient vs.angle of attack
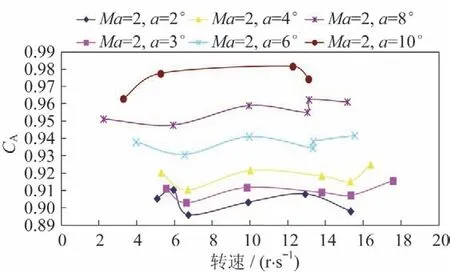
图17 阻力系数随转速变化曲线Fig.17 Drag coefficient vs.rolling rate
5 结束语
本文针对鸭式布局旋转导弹的舵翼干扰问题进行了研究。通过风洞旋转测力试验,对鸭式布局旋转导弹得出如下结论:
1)可采用多点平均法提供弹体纵向气动特性,可用准定常方法进行分析旋转导弹的纵向气动特性;
2)不同舵翼周向角的压心波动表明此类导弹在小攻角下的洗流干扰十分强烈,纵向气动性能波动较大;
3)马格努斯效应(包括马格努斯力系数和力矩系数)随转速变化波动较大,非线性较强,且在较大攻角下产生的侧向气动力系数随攻角增大而振荡加剧。

