高效高精度全局优化算法及其气动应用研究

徐圣冠，陈红全，张加乐，高缓钦，贾雪松

（南京航空航天大学航空学院非定常空气动力学与流动控制工信部重点实验室，江苏南京 210016）

0 引 言

现代比较流行的随机性启发式算法如遗传算法（genetic algorithms，GAs）、粒子群算法（particle swarm optimization，PSO）、模拟退火算法等（simulated annealing，SA），虽然具有全局搜索能力，但它们同时也存在收敛速度慢、需要函数评估次数多等缺点，对于函数评估比较耗时的工程问题（如基于计算流体力学的优化问题），其计算量有时是不能接受的。另一类基于梯度的优化方法又严重依赖于搜索起点，极易陷入局部最优解。针对经典优化算法的不足，一种新的基于代理模型（surrogate model）优化的方法为人们所青睐。它以一个代理模型的函数来代替耗时很高的精确模型的评估，能保证在一定精度的范围内快速得到最优解。代理模型按照优化过程中的构造方式，又可以分为静态代理模型和动态代理模型。动态代理模型由于在优化过程中不断优化样本空间，较静态代理模型有更高的搜索效率和精度。Kriging代理模型由于其在获得预测点预测值的同时能获得此处预测值的标准方差，因此很适合构造动态代理模型。在此基础上，Jones等提出了基于Kriging代理模型的高效全局优化（EGO）算法，此算法以改善期望（EI）函数作为最优加点策略，并用一组经典的测试函数作了测试，发现其用较少的样本点就能得到一定精度的全局最优解。

经典的EGO算法虽然能高效地获得全局最优解，但其精度仍存在进一步改善的空间。这一方面是由于EGO算法是基于代理模型的，本身就存在一定的误差；另一方面，目前没有一个很好的收敛判断准则，导致EGO算法容易过早收敛，对于这一点，文献［9］作了具体分析和研究，本文不再作具体讨论。

本文围绕最优解精度进一步改善的问题，研究了三类面向精确最优解的EGO算法。第一类算法考虑了与成熟的拟牛顿法和Powell法等局部优化方法的协同作用，第二类算法考虑在经典EGO算法的改善期望函数中引入Kriging信任的作用。在对几个常用检验函数验证结果分析比较的基础上提出了两者优缺点互补的第三类算法，并进行了验证。结果表明，三类方法都能够以相对较少的函数评估，得到比经典EGO算法更为精确的全局最优解。最后，本文选择第三类算法并采用N-S方程流场求解器对一个具有10个设计变量的跨声速翼型进行了优化验证，发现阻力系数在原有EGO优化算法的基础上有了进一步的下降。

1 EGO算法的基本理论

1.1 Kriging代理模型

Kriging 代理模型是一种估计方差最小的无偏估计模型，最早由南非的Krige 在1951年提出。它可以表示为如下数学形式：

式中：f()为已知的退化模型；β为相应的相关系数；()是一个均值为0、方差为的随机函数。()的设计点x和x（、=1，2，…，，为样本点个数）之间的协方差矩阵可以表示为

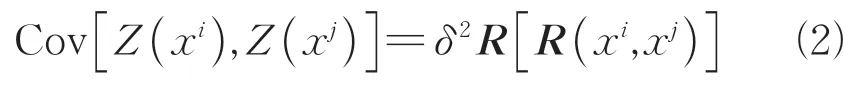
式中：是一个相关矩阵，它和数据点之间的空间分布相关。是一个对称矩阵，其中一种常用的函数形式如下：

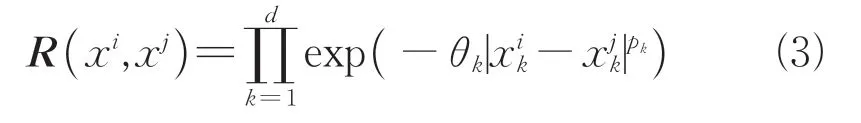
式中：θ≥0；0 ≤p≤2。θ值的大小反映了函数在第个坐标轴上的非线性度，值越大表示非线性度越高。p值的大小反映了函数在第个坐标轴上的光滑程度，其中常取p=2，此时函数被模拟为光滑函数。

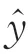
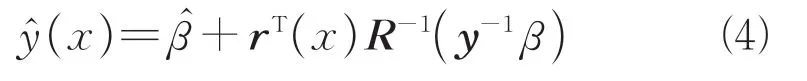
式（6）中包含了新加入的预测点所带来的误差，通常这个值很小，可以忽略，于是得到一个简化的均方差MSE估计公式：

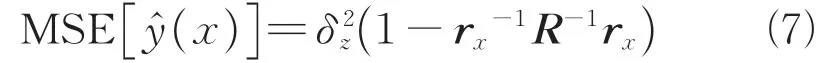
式（3）中的相关参数θ可由最大似然估计（MLE）在θ＞0的基础上最大化下式得到：

式中：

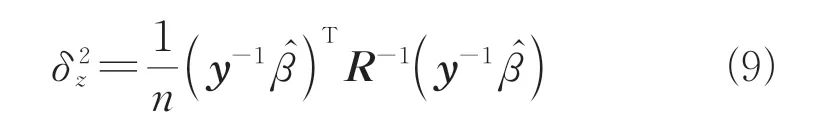
1.2 改善期望函数EI

改善期望（expected improvement，EI）函数作为经典EGO 算法的核心部分，是使EGO 算法具有全局性和高效性的重要保证。

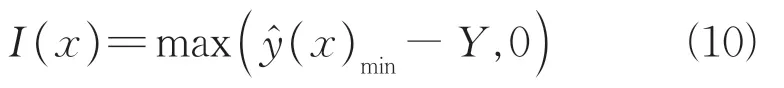
它的概率为

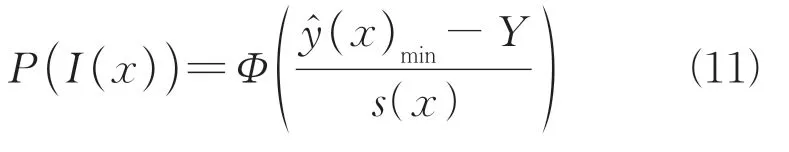
进一步得到期望为

式中：为标准正态分布函数；为正态概率密度函数。

从式（12）可以看出，无论是预测点值较小还是模型预测精度较低，都能使EI函数值变得较大，使最佳改善点偏向此处，这也是EGO算法具有高效性的原因所在。

1.3 经典EGO算法的基本流程

经典EGO的基本流程如下：

1）在设计空间中按照一定的试验设计方法（DOE）生成初始样本点；

2）以这个初始样本空间通过子优化相关系数构造Kriging代理模型；

3）以这个代理模型为基础对其进行最优值搜索，得到此模型的最优值；

4）以这个模型及模型的最优值为基础最优化EI函数，获得EI极大化时的最佳改善点；

5）判断是否满足终止条件，若满足，对这个模型进行最优值搜索，输出最优值，优化过程结束；若不满足，则转到第6步；

6）对这个最佳改善点用高精度函数评估得到改善点的响应值，加入样本空间回到第2步。

在本文中，试验设计方法采用拉丁超立方（LHS）采样方法，初始样本点个数全部取为5 个。对于EGO 算法中的两个子优化问题，由于类似于函数优化，本文则采用自适应遗传算法（AGA），并加入了自适应变化的多点交叉技术和生存压力函数来改善AGA 的全局寻优能力，并采用了Open-MP 并行加速技术来加速整个优化过程。

2 高效高精度EGO算法

基于Kriging 代理模型的经典EGO 算法有其固有的近似性。要消除这种近似性，本文考虑在最终寻优过程中不使用代理模型的替代方法。

2.1 EGO与局部优化协同算法

由于基于梯度等优化算法具有强大的局部搜索能力。考虑EGO 算法和此类局部优化算法协同，在EGO 算法收敛时用局部优化算法继续搜寻，消除EGO算法中代理模型带来的误差，进一步地搜寻得到更为精确的最优解。本文选择了比较成熟的需要计算梯度的拟牛顿法（BFGS）和不需要计算梯度的Powell法。

BFGS 法是目前为止不用Hessian 矩阵的算法中最有效的算法，被公认为是最好的拟牛顿法。它是由Broyden、Fletcher、Goldfarb 和Shanno 于1970年各自从不同角度出发得到的。本文采用的有限内存BFGS 方法是由Nocedal在1980年提出的，简记为LBFGS 方法。此方法无需记忆矩阵，解决了存储量大的问题，非常适合解决大规模问题，具体过程参见文献［17］。

Powell法和其他局部优化方法相比，其最大的特点是不需要计算梯度。因为对目标函数的解析性质要求不高，所以适用范围比拟牛顿法等需要求解梯度的优化算法更为广泛。但由于不利用函数的解析性质，因此其收敛也可能较慢，具体过程参见文献［18］。

本文考虑EGO算法和局部优化算法的协同作用，其过程可描述为：当EGO 算法收敛时，用LBFGS 或Powell 算法以EGO 算法得到的最优解作为起点进行最优化搜索，直至收敛。为下文中描述方便，这两种方法分别简记为EGO-LB和EGO-P。

2.2 改善最优加点策略

与传统的EGO算法不同，本文考虑在最终最优解的搜寻过程中（见1.3节算法流程第5步），不是基于代理模型，而是直接基于样本点寻优，这样就绕开了最终代理模型带来的近似性。但这样做有一个明显的缺点，就是要求全局最优解对应的点必须包含在最终的样本空间里面。EI 最优加点策略在计算后期由于全局最优解附近改善点大量聚集，使得该区域的标准差变得非常小，在后期会使最佳改善点偏向外围区域，造成全局最优解对应的最佳改善点很难被搜寻到，因此考虑对EI最优加点策略进行改善。

本文采用考虑KB作用的EI最优加点策略。在优化开始阶段采用EI最优加点策略，在EGO算法收敛时，改用KB法作为最优加点策略。当KB得到的最佳改善点和前一步所得到的重合时返回EI，如此往复，直至收敛。为下文中描述方便，此算法简记为EGO-K。

2.3 数值验证

本文选用文献中常用的测试不同复杂度的3个检验函数。

1）Branin函数

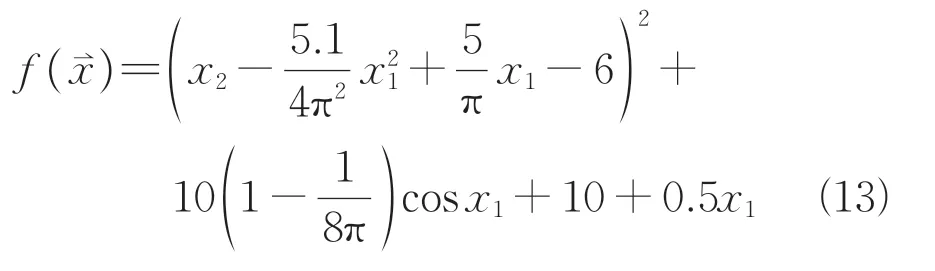
式中：-5 ≤≤10，0 ≤≤15，该函数的最小值为-1.185 9。

2）Hartman3函数

0 ≤x≤1（=1，2，3）。该函数的最小值为-3.862 8。

3）Hartman6函数

0 ≤x≤1（=1，2，…，6）。该函数的最小值为-3.322 4。

采用上述发展的EGO、EGO-LB、EGO-P 和EGO-K 算法，对以上3 个函数进行了数值实验，其结果如表1所示，表中数据从上往下依次为相对误差和得到最优解时的函数计算次数。

表1 数值验证结果及对比Tab.1 Test function results and comparisons

从表1中可以看出：

1）本文发展的EGO 算法比经典的EGO 算法具有更高的搜索效率和精度，这是由于本文在子优化过程中采用的是具有很强全局搜索能力的AGA 算法，而经典EGO算法采用的是直接算法。

2）EGO 算法与局部优化算法协同来提高EGO算法精度的代价是高昂的，其函数计算次数要比原有的EGO算法多出一倍左右，并且会随着问题规模和问题复杂程度的增加而增大。但相比于其他优化算法，与局部优化算法协同的EGO算法还是有巨大优势的，如对于Branin 问题，其他比如GAs 算法要计算300 多次才能得到函数值的最优解。

3）从搜索精度上来看，EGO-LB、EGO-P 和EGO-K 算法中，除了EGO-K 中处理Hartman6 函数时最终还有点误差外（但也已非常接近最优解），其他几种方法对于这3 个测试函数都能达到精确的全局最优解。

4）从搜索效率上来看，EGO-LB 效率最差，需要额外计算的函数次数最多，这和它需要计算函数梯度有关。表1中EGO-K 的函数计算次数包括中间判断初步收敛的次数，实际当KB 启动时分别只经过了7次、4 次和2 次就达到了全局最优解。从图1中Hartman6 函数收敛曲线中可以看到，当KB 发生作用时只经过了2 次函数计算就达到了最优解，搜索效率非常高。EGO-P 计算效率介于EGO-LB 和EGO-K之间。

图1 EGO/EGO-K优化Hartmat6函数收敛过程Fig.1 Convergence process of Hrtman6 function with EGO/EGO-K algorithm

5）从比较中可以看出，采用考虑Kriging 信任的改善期望函数的EGO算法具有很高的搜索效率，但当遇到高维复杂、初始模型构造误差较大的情况时，其精度不如与局部优化算法协同的算法，但后者的效率又大不如前者。既然两者优缺点互补，那么将两种方案协同作用在理论上应该可行。下一节讨论两者优缺点互补的改进算法。

2.3 改进算法

在EGO算法和局部优化算法协同作用的过程中，改用考虑Kriging信任的改善期望函数，形成全局优化的改进算法，简记为EGO-KLB 和EGO-KP，分别代表本文的EGO-K 算法与LBFGS 法、Powell 法耦合的算法，程序流程如图2所示。

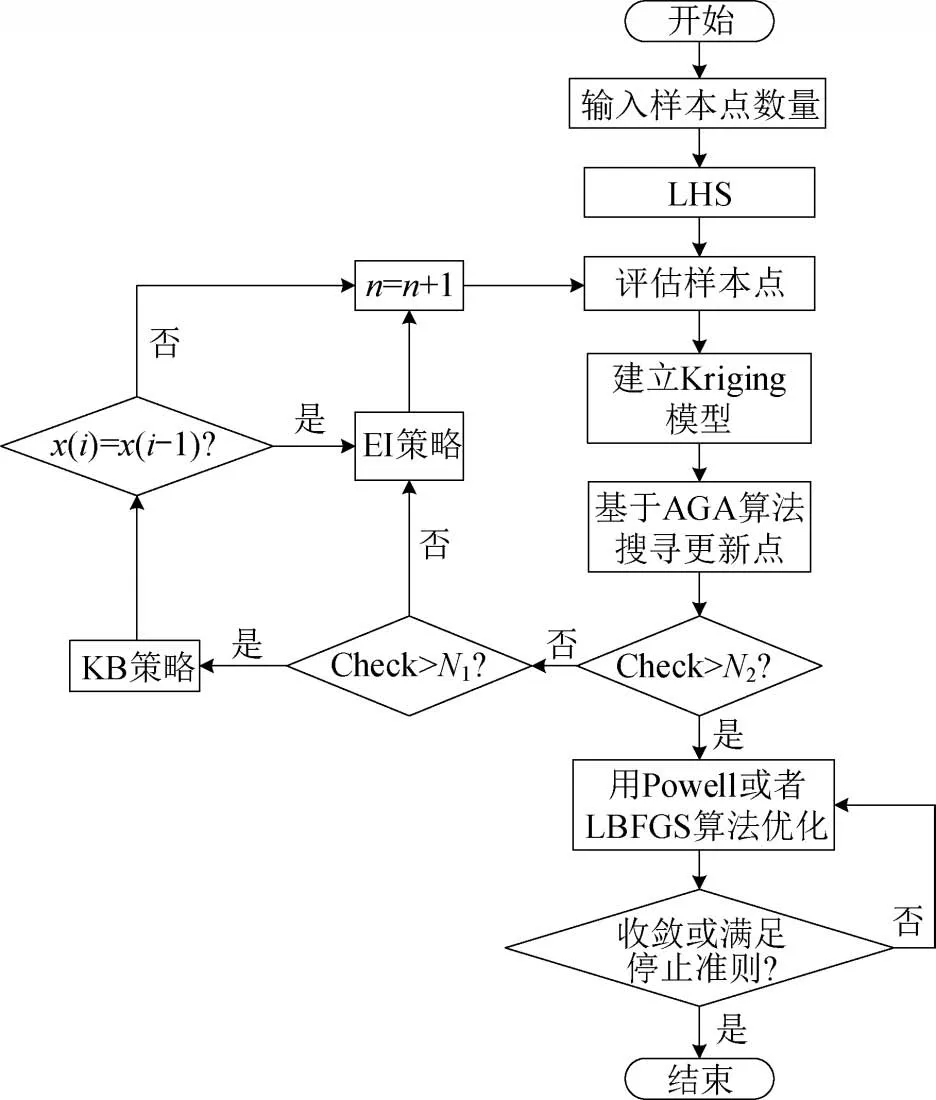
图2 EGO-KLB/EGO-KP程序流程Fig.2 Flow chart of EGO-KLB/EGO-KP

对Branin函数和Hartman3函数，两种方案都能得到精确的最优解，故这里取Hartman6 函数来验证算法。这里两个判断参数取为=10，=15，为2%精度范围内连续不变代数。

由表2可以看出：EGO-KLB 和EGO-KP 在得到Hartman6函数精确最优解时，所用的函数计算次数分别比EGO-LB 和EGO-P 减少了10.5%和7.9%，比经典EGO 算法获得精确全局最优解的函数计算次数分别减少了8.3%和31.0%。由此说明，此方案在获得精确最优解的同时，能降低改进EGO 算法和经典EGO算法的函数计算次数，说明此优化算法在一定程度上是有效可行的。

表2 改进算法数值验证结果Tab.2 Test function results of the improved EGO

3 跨音速翼型优化算例

为了验证本文面向精确最优解的EGO 算法的工程价值，选取了跨音速翼型阻力极小化优化算例来进行验证。优化算法选取了精度和效率相对都比较高的EGO-KP法。

本文以RAE2822为参考翼型，设计要求是在来流马赫数0.729、攻角为2.55°、雷诺数为6.5×10时，翼型的阻力最小，同时要求翼型的截面面积和升力系数在一定范围内不减小。此时该优化问题可以表示为

适应度函数取为

升力系数约束罚函数为

面积约束罚函数为

翼型参数化方法采用CST 参数法。CST 参数法能以较少的参数表达完整的翼型信息，具有使用方便、直观、控制参数可控等优点。本文取了10 个设计参数。

流场解算器采用Fluent 耦合隐式N-S 方程求解器，湍流模型采用S-A全湍流模型，采用多重网格加速技术，计算网格量为36 024 个。本算例中取两个判断参数=80，=100（即当代最优值保持不变时，KB 开始作用；代最优值保持不变时，Powell 法开始作用）。优化结果和收敛曲线见表3和图3，从中可以看出：EGO 算法在计算67 次流场以后，就收敛到了全局最优解附近；在经过80 次最优值保持不变以后，改用KB 和Powell 法，可以看出KB 和Powell 法使最优解在原有的基础上再次提高了1.11%；同样，EGOKP 算法的函数计算次数中也包括了判断初步收敛的80次函数计算。

表3 CD优化结果及对比Tab.3 Optimization results and comparison of CD

图3 翼型优化收敛曲线Fig.3 Convergence curve of the airfoil optimization

表4给出了本文最终优化得到的翼型和RAE2822的对比。从表4中优化结果可以看出：优化翼型阻力系数比RAE2822翼型减小了11.38%，升力系数和面积略有下降，但都在约束允许范围之内。图4给出了优化后翼型与RAE2822翼型的外形对比，其中，为翼型弦长。从图5～7中可以看出：优化后翼型表面的激波已基本消失，表明优化得到的阻力减小主要源自激波减阻。

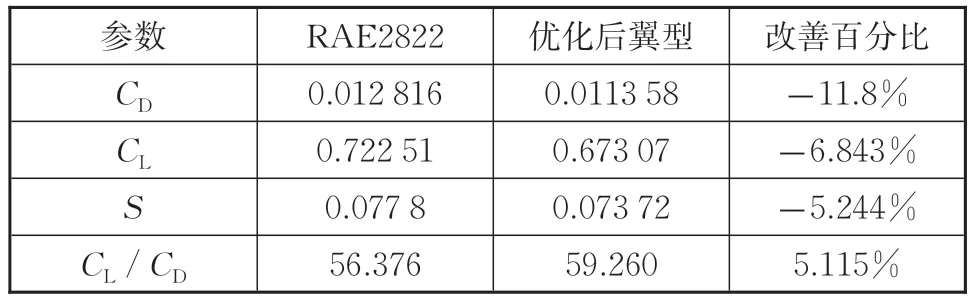
表4 优化结果和参考翼型对比Tab.4 Optimization results and comparison

图4 优化翼型与初始翼型外形对比Fig.4 Sharp of the optimized airfoil and RAE2822

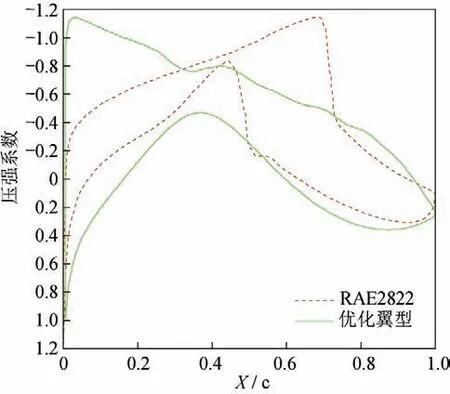
图5 优化翼型与初始翼型压强系数对比Fig.5 Pressure coefficient of the optimized airfoil and RAE2822

图6 RAE2822翼型压强系数等值线Fig.6 Pressure coefficient contour line of RAE2822

图7 优化翼型压强系数等值线Fig.7 Pressure coefficient contour line of the optimized airfoil

4 结束语

为了提高EGO 算法的优化精度，本文发展了与Kriging 信任法、牛顿法、Powell 法等局部优化算法协同的优化算法。整体上，本文所发展的改进算法都能以相对较少的额外函数评估，得到比经典EGO 算法更精确的全局最优解。具体地，第1 类改进的EGO与局部优化协同算法（EGO-LB 和EGO-P）得到的全局最优解具有较高的精度，但效率相对较低；第2 类考虑Kriging 信任的改善期望函数的EGO 算法（EGO-K）具有很高的效率，但高维测试函数算例得到的最优解，其精度不如第1 类算法；第3 类改进算法（EGO-KLB 和EGO-KP）耦合了第1 类和第2 类算法的优点，能以比经典EGO 算法更少的函数评估，获得更精确的全局最优解。最后，把发展的算法应用到具体的跨音速翼型优化问题中，优化结果显示，得到的阻力较原EGO 算法有进一步的减小，优化翼型上的激波基本消失（基本无波阻），展示了一定的工程价值。