细长旋成体大攻角非对称涡模拟的扰动引入方式研究

张绍广，肖茂超，张宇飞，陈海昕

（清华大学航天航空学院，北京 100084）

0 引 言

导弹和飞行器需要在大攻角工况下飞行，因此必须研究大攻角下旋成体的流动结构，才能保证在大攻角工况对导弹和飞行器的精确控制。小攻角时（0°≤≤15°），旋成体生成附着对称的涡结构；在中等攻角时（15°＜≤30°），旋涡脱体但仍然维持对称结构，此时产生的侧向力可以忽略不计；在大攻角时（30°＜≤65°），受对流不稳定性影响，旋涡变得不对称和非定常，侧向力也变得显著。在大攻角时（30°＜≤65°），侧向力甚至超过法向力，从而将导致较大的不良偏航力矩。

侧向力的产生与很多因素有关，如雷诺数、攻角、马赫数和导弹前体形状等。Lamont等研究了不同雷诺数对侧向力的影响：基于导弹直径的雷诺数Re为0.2×10和4.0×10时，分别为层流分离和全湍流的分离；Re在0.4×10至0.8×10的范围时，分离剪切层中存在转捩；在攻角小于70°时，层流分离和全湍流的分离非常相似，相比存在转捩的分离产生更加显著的侧向力。Kumar等发现导弹侧向力的产生主要是由模型的不完美导致的，而且在实际生产制造过程中很难制造出完美的模型。Keener等在研究中指出，导弹在不同滚转角时会产生不同的侧向力，侧向力的不同主要取决于导弹前体20%的长度位置，单独旋转前体和旋转整个导弹产生的侧向力基本一致。有学者在数值计算中发现，在导弹的头部设置扰动可以计算出不对称的涡结构。Lim等在导弹前体采用不同的层流-湍流转捩条件，捕捉到了旋涡的不对称结构。

主动和被动的流动控制方法（如：扰流片、钝头、圆形转捩带、头部凹坑、吹吸气等）被用来控制导弹大攻角时侧向力的产生。对这些流动控制方法的研究，大多采用试验测试的方法进行，效率往往较低。但是，目前采用数值计算的方法发展减小侧向力的流动控制方法依然很难实现。主要的原因在于，数值计算中需要引入微小的扰动才可以捕捉到不对称的流动结构，扰动的位置和尺寸都需要根据试验值来确定。

研究导弹大攻角非对称分离形态和侧向力的变化规律需要准确的预测模型。迄今为止，雷诺平均方程（Reynolds-averaged Navier-Stokes，RANS）仍然是计算工程湍流问题最常用的方法。RANS 方法采取系综平均的思路，将湍流信息分解为平均量和脉动量，脉动量在Navier-Stokes 方程中通过雷诺平均转化为雷诺应力的形式，然后利用湍流模式对其进行模化。但是RANS方法在计算分离流动时会产生较大误差，尤其不适用于预测大分离流动。与RANS 方法对比，大涡模拟（large-eddy simulation，LES）方法采取空间过滤的思路，将流场信息分解成大尺度低频脉动和小尺度高频脉动。但是，采用LES方法解析边界层的计算量很大。Spalart指出，使用壁面解析的LES（wall-resolved LES，WRLES）百万雷诺数的机翼边界层流动，需要网格数量为10量级，时间推进步数为10量级，计算量远远超过了现代计算机的计算能力。为了克服LES在模拟高雷诺数湍流边界层时的计算量过大的问题，可以采用RANS 方法模化整个边界层，即脱体涡模拟（detachededdy simulation，DES）方法。近年来，虽然DES 方法仍然存在一些问题，但是该方法还是得到了广泛的应用。目前，关于DES 方法的研究主要集中于如何缓解DES方法的“灰区”问题。

改进的延迟脱体涡模拟（improved delayed detached-eddy simulation，IDDES）方法是DES方法的一种改进型，但其依然存在“灰区”问题。为了解决IDDES 方法存在的“灰区”问题，本文提出了一种剪切层自适应的IDDES 方法。选取了具有可靠试验数据的导弹标准算例，通过引入适当的扰动，对导弹大攻角非对称的分离形态进行了详细分析；介绍了数值模拟中，准确预测细长旋成体大攻角侧向力的方法。

1 几何模型与网格

图1展示了本文中数值计算采用的导弹模型尺寸示意图。其前体为Tangent曲线成型，弹体的直径为152.4 mm，轴向长2；后体为轴对称圆柱体，轴向长度为13。试验测试了不同雷诺数、不同攻角时导弹侧向力的变化，本文的计算中基于导弹直径的雷诺数Re为3.0×10，来流马赫数为0.2。

计算中采用结构网格对计算域进行离散，图2展示了弹体表面网格、攻角平面-的网格和垂直于攻角平面-平面的网格。弹体的轴向共布置了287个节点，垂直于弹体转轴的截面上共布置328 个点，全模的总网格量为2 500万。为了很好地捕捉导弹大攻角下的涡结构，在弹体的背风面进行网格加密，背风面的网格占总网格的65%左右。为了排除数值计算带来的不对称干扰，网格生成过程中首先生成导弹半模的网格，在将网格对称生成全模的网格，从而保证计算网格的完全对称，排除网格的干扰。Kumar等在研究中发现，在数值计算中想准确地预测试验中测得的侧向力，必须添加适当的扰动。本文在计算中采用了文献［9］中提出的添加扰动的方式，在轴向距离导弹的头部0.08的位置，-平面内，安装最大高度为0.004，长度为0.04，最大宽度为0.004的扰动，几何尺寸如图1所示，头部扰动位置网格如图3所示。

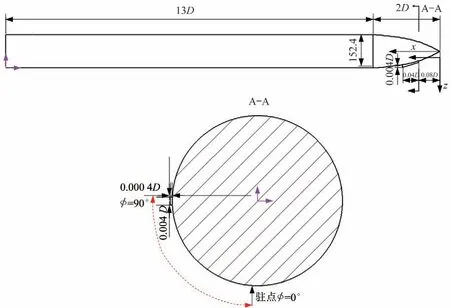
图1 导弹模型尺寸示意图Fig.1 Schematic diagram of missile model size

图2 导弹全局网格和头部网格Fig.2 Global mesh and mesh around the missile head

图3 扰动及其网格Fig.3 Perturbation and the grids

2 数值方法

2.1 原始的SST-IDDES方法

为了解决IDDES 方法存在的“灰区”问题，发展了剪切层自适应的IDDES 方法。本部分对原始的剪切应力传输IDDESS（shear-stress transport-IDDES，SST-IDDES）方法的框架进行简单的介绍，从而方便对剪切层自适应尺度的描述。IDDES 方法通过将RANS 的长度尺度替换为IDDES 长度尺度得以实现，IDDES 的湍动能的输运方程如式（1）所示。

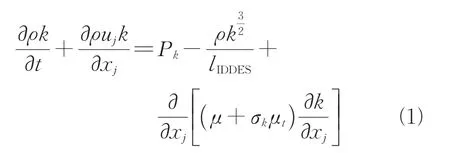
式中：为密度；为时间；为湍动能；为层流黏性；μ为涡黏性；P为湍动能的生成项；IDDES 的长度尺度表达为

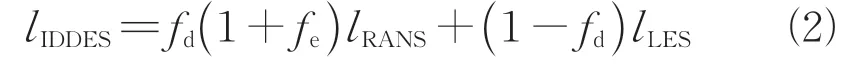
式中：＞0 时为提升函数，增加RANS/LES 切换之前RANS 区的涡黏性，避免此区域的涡黏性过度减小；当来流不存在湍流度时，=0，IDDES 表现为DDES；为切换函数，详细公式见文献［19］。

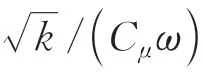
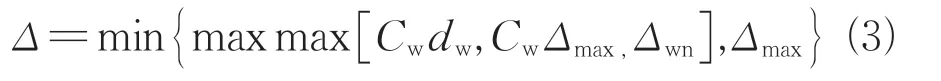
式中：常数=0.15；为网格单元中心到壁面的距离；和分别为网格单元最大长边和网格在壁面垂直方向的网格尺度；切换函数=max{(1-)，}，其中与流动相关，用于控制IDDES 分支中RANS/LES 的切换，仅与网格相关，用于控制壁面模化的大涡模拟（WMLES）分支中RANS/LES 的切换。在来流或者初场存在湍流脉动时，=，IDDES变现为WMLES，对应的长度尺度为

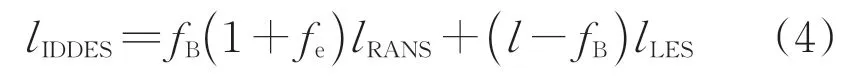
式中：＞0 为提升函数，增加RANS/LES 切换之前RANS 区的涡黏性，避免此区域的涡黏性过度减小。当来流不存在湍流度时，=0，IDDES 表现为DDES，=1-，对应的长度尺度为

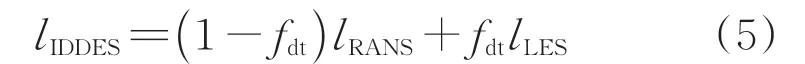
2.2 剪切层自适应长度尺度

剪切层自适应长度尺度公式如式（6）所示。

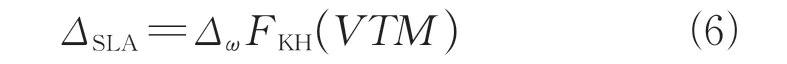
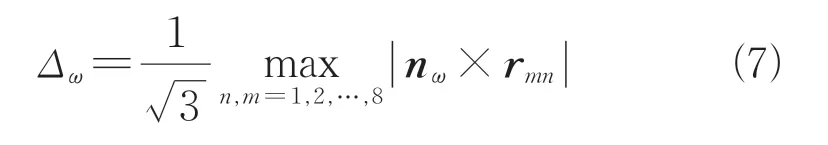
式中：Δ为涡量矢量方向的网格尺度；n为单位化的涡量矢量；r(，=1，2，…，8)为网格单元任意两顶点构成的矢量。

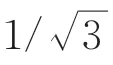
3 结果与分析

图4展示了计算得到的无量纲准则瞬时等值面，等值面采用马赫数进行着色。准则定量反映了流场中的相干结构，可以用应变率和涡量的函数来表示，即

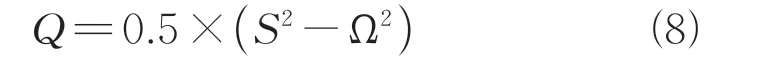
由图4可以看出：没有添加扰动时，导弹背风面生成稳定的一对旋涡，旋涡由导弹头部脱出，逐渐向下游发展，在整个弹体的长度上都没有出现涡破碎；添加扰动之后，旋涡在三分之一弹体长度的位置处出现涡破碎，发展成为完全不对称的涡形态。

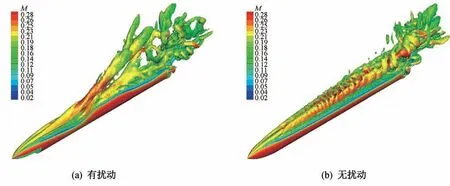
图4 有/无扰动导弹涡结构示意图Fig.4 Vortex structure diagram of missile with/without perturbation

图5展示了导弹不同轴向位置截面的压力分布，图中黑色圆圈表示试验测量值，蓝色点表示不添加扰动时的计算值，红色实线为添加扰动的计算值。试验测得的压力分布明显为非对称结构，左侧的压力分布吸力峰值更高，右侧更低。不添加扰动时计算得到的压力分布在不同轴向位置基本为对称的分布，添加扰动后计算得到的压力分布为非对称结构，且与试验结果吻合很好。证明了本文添加的扰动是合理的，发展的数值方法也可以准确地预测导弹大攻角下的侧向力。

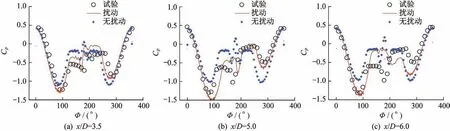
图5 有/无扰动导弹压力分布Fig.5 Pressure distribution of missiles with/without perturbation

图6和图7分别展示了无/有扰情况下不同展向位置截面的流线与马赫数分布云图：无扰动时不同轴向位置截面几乎都为对称的涡结构，随着向下游发展涡核逐渐增大；添加扰动后，右侧分离明显提前，速度降低，压力升高，所以产生方向为的负方向的侧向力（在不同轴向位置截面都为非对称的涡结构，如图7所示）。

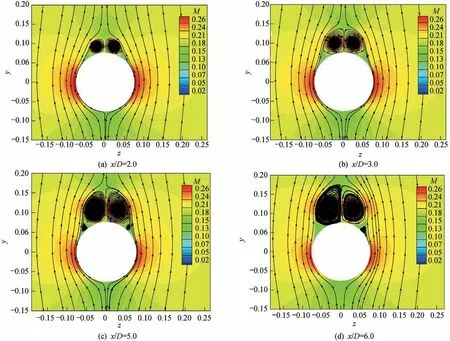
图6 无扰动时导弹不同轴向位置截面流线与马赫数分布云图Fig.6 Streamline and Mach number distribution contour at different axial sections of missile，without perturbation

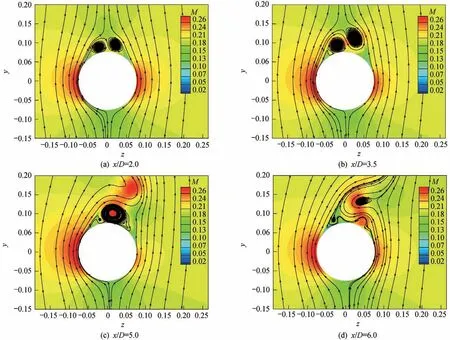
图7 有扰动时导弹不同轴向位置截面流线与马赫数分布云图Fig.7 Streamline and Mach number distribution contour at different axial sections of missile，with perturbation

4 结束语

采用数值计算的方法研究了导弹侧向力产生的原因，分析了扰动对导弹侧向力的影响。数值方法描述试验中产生侧向力的现象，需要人为引入合适的扰动。采用带剪切层自适应的IDDES 方法，对有/无扰动的导弹构型进行了计算。采用完全轴对称的几何模型和对称的网格，在整个弹体的背风面生成对称的涡结构，不会发生涡破碎，几乎没有产生侧向力。在导弹头部设置扰流片引入扰动，会在导弹的背风面诱导出完全不对称的涡结构，在添加扰动一侧，分离会明显提前。分离提前使添加扰动一侧的速度降低、压力升高，从而产生侧向力。本文通过添加扰流片引入扰动，计算得到的压力分布与试验结果非常吻合。但是，较大的侧向力不利于导弹的飞行控制。需要设计合理的流动控制手段，抑制侧向力的产生，实现导弹大攻角下的精确控制。