考虑旅客等待时间的城际列车开行方案优化

杨云，张小强，1b，1c，乔晓青

（1.西南交通大学a.交通运输与物流学院，b.综合交通大数据应用技术国家工程实验室，c.综合交通运输智能化国家地方联合工程实验室，成都 611756；2.四川文理学院 建筑工程学院，四川 达州 635002）

随着我国城市化进程的加速，城市群逐渐成为城市发展的主要方向，城际旅客出行需求迅速增长，城际列车的作用越来越明显.目前全国已经开通了多条城际客运专线，根据铁路发展规划，我国铁路已经形成客运专线等相配套的3 万多千米的快速客运网络，这一网络覆盖人口达7 亿多，能够满足人们快速便捷出行的要求，城际列车因此向着更长远、持久的目标发展.从2020 年7 月开始，长三角城市群3 条城际线路率先试行“铁路e 卡通”扫码乘车，无需购票，随到随走，目前该模式已经扩展到全国许多城际线路.然而，人们的出行因时空而分布不均衡，大站和高峰期客流量较大，排队等待时间长，小站和低峰期客流量则较少，运能浪费.根据铁路总公司历年数据，我国高铁虽然发展迅速，但是大部分高铁线路处于亏损状态，对于市场化改革后的铁路企业，减少亏损是需要重点解决的问题.因此，如何提高城际列车开行方案的质量，对于减少铁路企业成本和乘客等待时间变得非常迫切.

旅客乘车等待时间方面，乘客乘坐公共交通时，若等待时间比乘车时间更冗长，则选择公共交通的意愿会受到强烈影响，因此减少等待时间非常重要［1］.Shi等［2］建立严格的综合整数线性规划模型，尽量减少所有车站的总等待时间.针对周期开行城市快速列车，Barrena等［3］提出4 种优化模型，旨在最小化乘客的平均等待时间.Nachtigali等［4］建立乘客换乘列车以最小等待时间的时间表计算模型.邓晓蓉［5］给出了轨道交通网络普通站和换乘站乘客候车时间的计算模型.李登辉等［6］基于Fisher 最优分割法确定合理客流控制时段，优化了成都地铁高峰线路乘客总等待时间.靳国伟［7］给出高速铁路平均等待时间的计算公式，为运营周期除以开行数量的两倍.王媛媛等［8］提出城市轨道交通旅客等待时间的计算方法.史峰等［9］针对车站需求稀疏时段，提出发车时间间隔上限要求来提升高铁服务水平.上述研究主要集中在城市公交和轨道交通，多把等待时间作为一个固定值纳入乘客总旅行时间，通常取开行间隔的一半，这对于发车和停站时间间隔不等的城际列车则有较大的出入.

在以成本为导向的列车开行方案优化的研究中，Bussieck等［10］设计启发式变量修复程序，以荷兰铁路公司的真实数据求解了成本最佳的列车开行方案.Yue等［11］提出一种优化高速铁路系统列车时刻表的数学模型，该模型既能满足客运需求，又能降低铁路运营商的成本.Torres等［12］在保证一定服务质量水平的同时最小化运营成本.史峰等［13］表明成本主要包括列车公里费用、车公里费用、车小时费用以及列车组织费用等.付慧伶等［14］建立成本最低的高速列车开行整数规划模型，得到优化后的开行方案能使服务指标较优.

对于等待时间和开行方案的综合优化，Borndörfer等15］提出了一个减少总旅行时间和运营成本的模型.Chang等［16］建立铁路总运营成本和旅客总出行时间最小的多目标规划模型，在给定的需求下生成目标最优的台湾高铁开行方案.戎亚萍［17］则以乘客总出行费用和企业运营成本最小为目标.许得杰等［18］建立城市轨道交通大小交路列车时刻表优化模型，在运营成本相等的情形下，乘客等待时间可减少16.5%.

在我国城际列车发展迅速的同时，列车服务质量极不均衡，由12306 官网数据可知，以京津城际等客流密集线路开行频率可达5 min/次，成巴城际等客流较少线路开行频率则达300 min/次.Lyapunov函数作为一种控制系统稳定性的优化算法，在控制理论方面应用非常广泛，主要用于寻求多时隙下的动态网络的全局最优，Lyapunov 漂移则是其稳定性控制的关键.Neely等［19］利用Lyapunov 漂移技术开发了一种动态控制策略，对通信时变网络流量积压进行了优化，在平均延迟下，实现了网络最大流量.大多学者对旅客时间费用的研究集中在旅行时间，城际列车运行速度基本固定，减少旅途等待时间和停站时间是缩短旅客旅行时间的主要依据.本文从旅客等待时间角度出发，对铁路企业成本和旅客出行效益进行优化.引入Lyapunov 方法控制旅客排队长度，构建描述多时隙下旅客排队长度与城际列车开行方案的优化模型，通过Little 公式［20］把旅客排队长度转换为旅客等待时间，实现对城际旅客等待时间与开行成本最小化进行协同优化.

1 问题描述和假设

1.1 问题描述

假设一条城际线路上有n个车站，各车站OD对旅客量为Nij(i，j=1，2，…，n)，城际列车由始发站发车，经过线路上的所有车站，到达终点站.在各站OD 对客流量和票价已知的情况下，决策者对城际列车的开行停站方案进行优化，以降低铁路企业的开行成本和旅客排队等待时间，提升城际列车服务质量.

1.2 模型假设

对列车开行方案建模之前，对问题相关影响因素做出假设：

1）考虑一条客运专线单向客流大小，旅客到达服从泊松分布；

2）以CRH3C 列车为例，假定列车定员为560 人/列，不考虑重联，不允许超载；

3）以5 min 钟时间段作为一个时隙，进行列车的开行和停站决策；

4）每个车站一趟车只有一个服务台，旅客到达时间间隔和服务时间服从负指数分布，排队模型为M/M/1 标准模型，先到先服务.

2 优化模型

2.1 列车开行成本模型

开行成本主要考虑列车的发车、停站成本以及列车停站时车上旅客等待成本.为了方便旅客的出行，开行方案的基本原则是以尽量少的车次最大程度地保证旅客直达，减少开行成本和停站次数.建立开行成本模型为

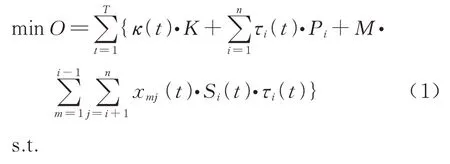
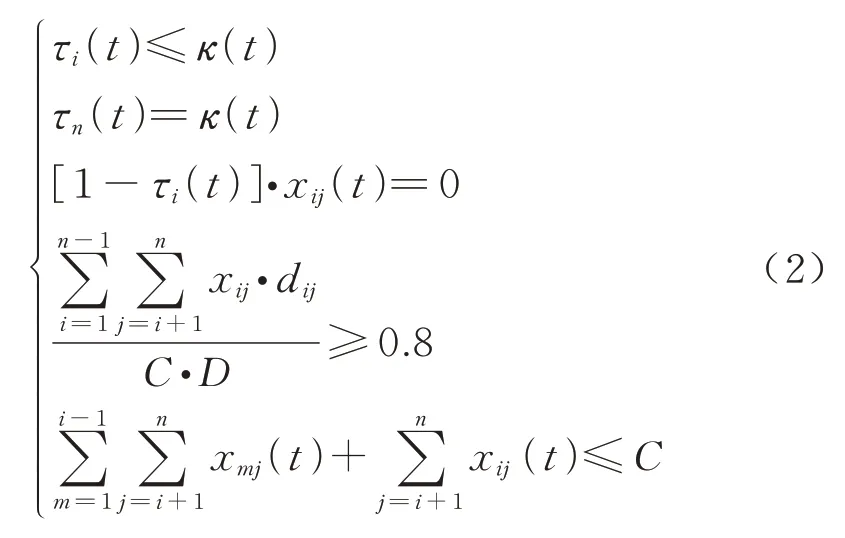
式中：t为列车开行时隙，t=1，2，…，T；κ(t)为0-1 变量，若κ(t)=1，在t时隙发车，反之不发车；τi(t)为0-1 变量，若τi(t)=1，表示在t时隙i站停车，反之不停站；m为车站序号；xij(t)为t时隙i站到j站实际乘车离开的旅客数；K为列车开行固定成本，元；Pi为列车在第i站停站成本，元；M为时间价值系数，元/min；C为列车定员人数；Si(t)为t时隙，列车在i站停站时长，min；dij为第i站到j站路程长，km；D为总路程长，km.式（2）中分别表示列车有开行才有停站；列车在终点站结束；若列车在i站不停站，则没有旅客上下车；列车席位利用率；t时隙i站上车的乘客数与车上乘客数总和应小于列车定员数.

2.2 城际列车旅客排队模型

在各个时隙，旅客依次来到车站排队乘车，未上车的乘客便会在车站产生排队.根据旅客的平均到达率和服务率，求解乘客平均排队等待时间.如果每个时隙都有未上车旅客，旅客队列一直增加，则会对整个线路产生影响.因此，旅客的排队问题本质上也是运输系统的稳定性问题.定义Qij(t)为整数时隙上离散时间i站到j站排队人数，由旅客到达和离去情况，相邻时隙队列长度变化动态表达式为

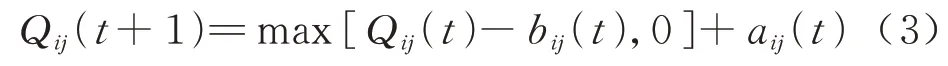
式中：aij(t)为t时隙i站到j站新增旅客数；bij(t)为t时隙i站到j站可离开旅客数.如果该时隙有列车发出或停站，xij(t)=min[Qij(t)，bij(t)]；如果该时隙没有列车发出或停站，则xij(t)=0，因此相邻时隙排队长度进一步可表示为

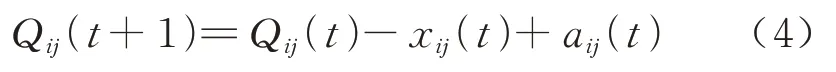
对于任意两时隙t1和t2，0 ≤t1≤t2，两时隙的排队长度为

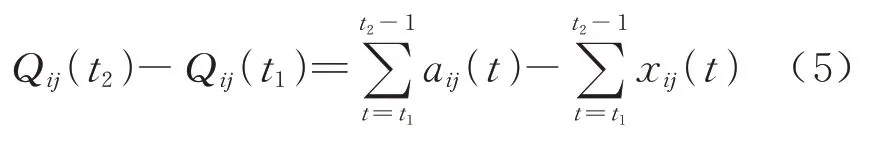
对于任意时隙的平均排队长度为

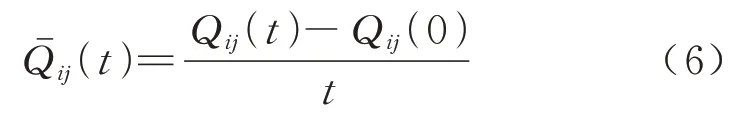
对一个周期而言，某OD 对旅客乘车排队平均长度为

如果t时隙有列车开行或停站，旅客于t时隙之前到达，排队乘坐该车次.根据Little 定理［21］，系统排队作为一个生灭过程，等待时间由服务率和到达率决定，而列车开行服务率比较特殊，由开行或停站时一次性乘车离开排队旅客数决定，旅客乘车排队等待时间W可表示为

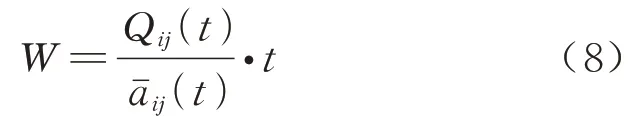
若某车站列车可以停站H次，则该站发车的某OD 对旅客乘车排队平均等待时间为

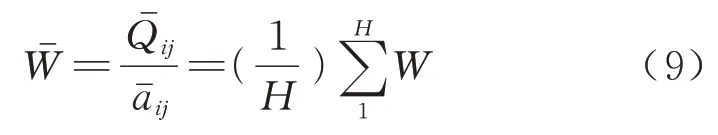
引理1：队列长度稳定定理.对于制定的列车开行计划，如果有列车发出或停站的时隙，排队的旅客乘车离开，xij(t)≠0.对于这些时隙，可计算出整个线路未上车的旅客平均队长为

因此，对于每个周期而言，制定的列车开行方案应保证旅客队列长度稳定.

2.3 Lyapunov 漂移排队长度变化界限模型

定义3：时隙t时，旅客排队长度的Lyapunov 函数表示为L(t)=

Lyapunov 函数L(t)反映了一个时隙t内队列的排队人数多少，最小化L(t)可使一个时隙客流排队人数趋于0.由于城际列车相邻时隙的决策相互影响，运输网络中的客流排队量不独立存在，前一时隙的客流排队数会影响下一时隙.定义一个时隙t内的Lyapunov 漂移Δt为

Lyapunov 漂移反映了相邻时隙t内的旅客队列的排队变化界限，由于B值固定，当最小化Δt时，即最小化Qij(t)·(aij(t)-xij(t))，则做出的开行决策，使Qij(t)·(aij(t)-xij(t))最小，相邻时隙排队旅客最少.

2.4 Lyapunov 漂移加罚模型

漂移加罚是一种保证旅客排队队列稳定性的同时，罚函数优化平均时间成本的方法，对列车开行成本和旅客排队数通过罚函数建立Lyapunov 漂移加罚模型.定义一个时隙t内的Lyapunov 漂移加罚ΔV(t)为

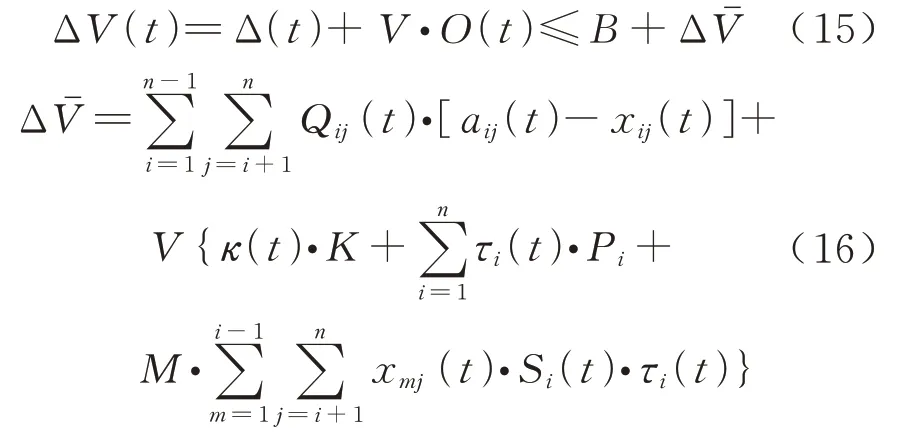
式中：V为非负权重系数.

故在漂移加罚中只需优化式（16）即可，开行成本模型转化开行成本与旅客队长协同优化模型为

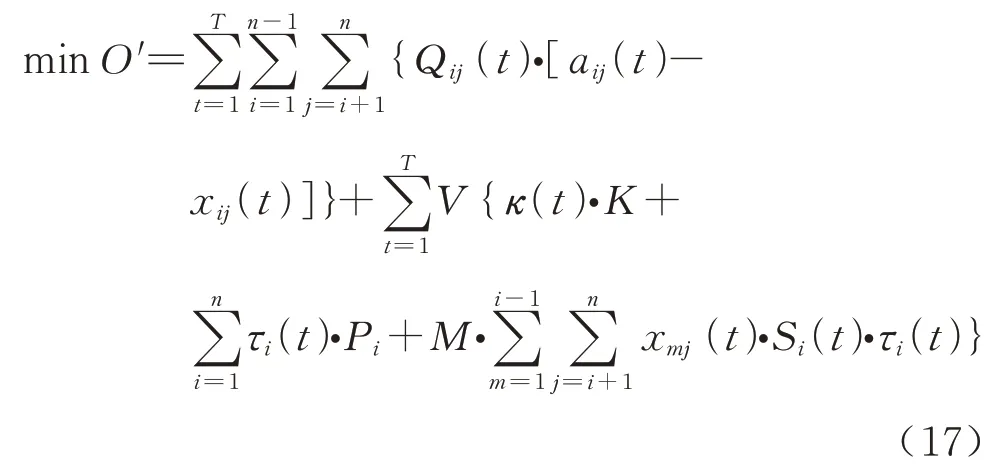
式（17）的约束为式（2）.

证明：在一个周期T内存在

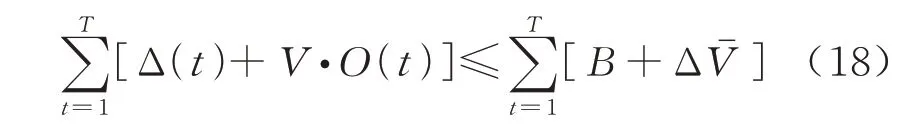
对不等式（18）两边时隙求平均可得

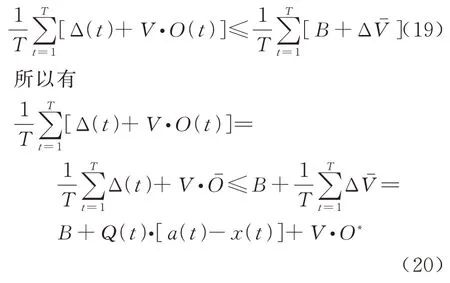
根据式（20）可得

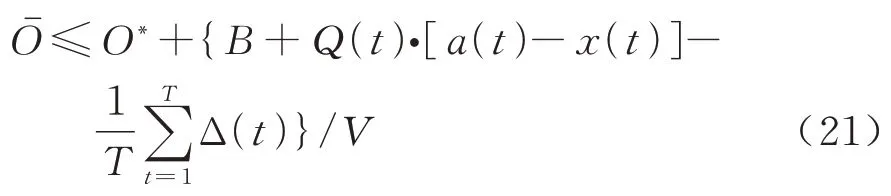
而B+Q(t)·[a(t)-x(t)]-Δt≥0，由于B*值非负，因此可得

式（17）反映了列车开行成本和客流排队特征，在算法求解的过程中，通过调整V值，可在保证网络队列稳定的前提下，使旅客队列长度和开行成本达到一个相对平衡，最终使整个目标最优，得到列车开行的最优方案.

3 算法设计

由于转化后的目标函数非凸，拟采用启发式算法求解.和声搜索（Harmony Search，HS）算法是一种新颖智能启发式优化算法，通过不断调整和声库的解变量，使函数值随着迭代次数的增加不断收敛，从而得到最优解.其类似于遗传算法等算法，但更简单，有针对性，收敛速度快、稳健性好，最大缺点是可能会陷入局部最优.因此，拟采用改进的和声搜索（Improved Harmony Search，IHS）算法进行求解，提高其全局寻优能力［21］，IHS 算法主要是采用动态的音调调节概率PAR，每次迭代PAR 的计算公式为

式中：gn 为算法当前迭代次数；GERmax为最大迭代次数.

IHS算法流程见图1，具体实现步骤分为5个步骤.

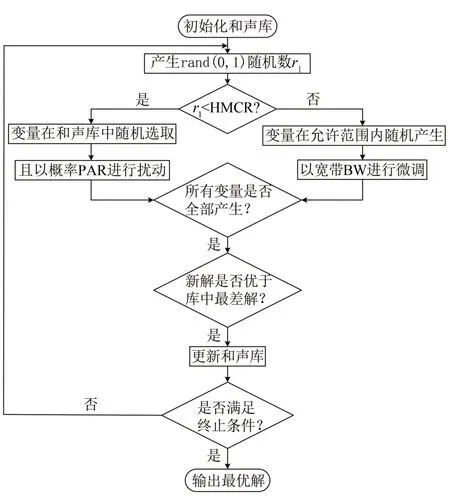
图1 IHS 算法流程图Fig.1 Flowchart of IHS algorithm

步骤1：确定所有参数取值.

步骤2：初始化和声记忆库HMS.由解空间随机生成一个大小为HMCR 的和声库.

步骤3：生成一个新和声.在［0，1］中产生随机数r1，与HMCR 比较.若r1＜HMCR，在和声库中随机拿出一组和声，否则在解空间中随机生成一组和声.如果这组和声是从和声库中得到，则以微调带宽BW 来对和声进行调整，每次迭代BW 计算公式为

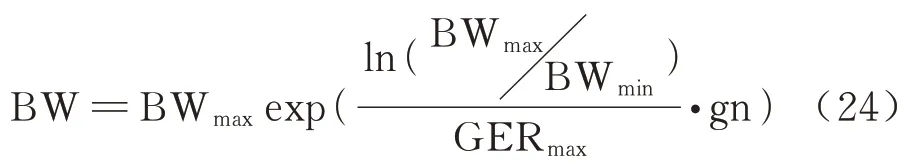
式中：BWmax、BWmin为最大和最小宽带值.

进而得到一个新和声.

步骤4：更新和声记忆库.根据新和声求得适应度值，如果比初始化的和声库中的值差，则替换掉和声库中那个最差的和声.

步骤5：检查算法是否中止.迭代是否达到最大次数，否则重复步骤3 和步骤4.

4 算例分析

成遂渝高铁作为一条分担成渝城市群旅客出行的城际线路，总长274 km，由遂成铁路与遂渝铁路共同组成，线路主要车站及各路段里程如图2 所示.该线路票价为96.5 元，运行时间约为2 h，其票价比成渝高铁城际列车低了近40%，吸引着许多中等收入及以下的旅客出行.根据2021 年成渝客专公司数据，成遂渝高铁平均每天开行20 对城际列车，单向载客量约为12 000 人.以成都到重庆为例，由于其开行车次不多，开行时间间隔较大，车次主要集中上午，存在下午乘车难和旅客排队等待时间较长的问题.因此，本案例对该线路开行方案进行优化.模型和算法主要参数取值见表1.

图2 成遂渝城际列车线路图Fig.2 Route map of Cheng-Sui-Yu intercity high-speed train

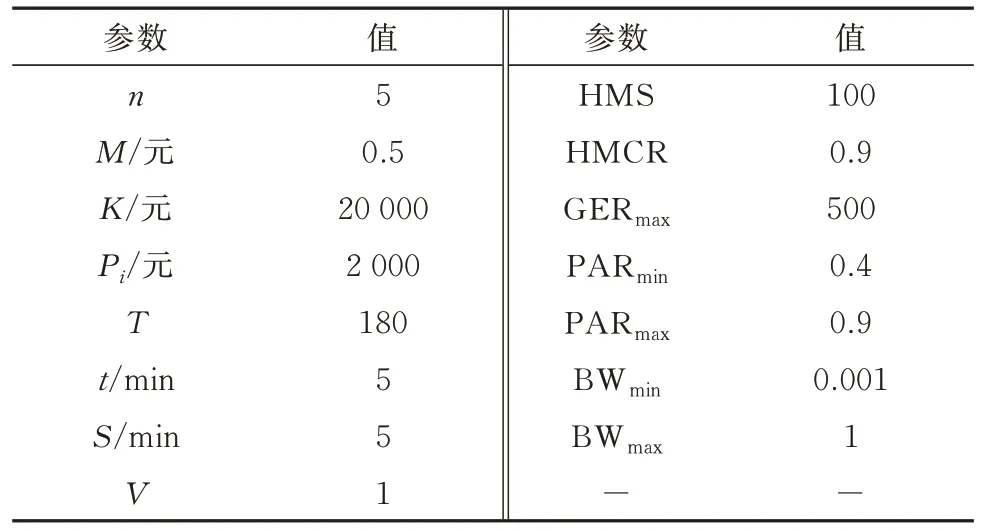
表1 参数取值表Tab.1 Parameter values

根据车站城市的GDP、人口总量和联系紧密程度等因素，估算各OD对的客流量占总客流量的比例见表2.

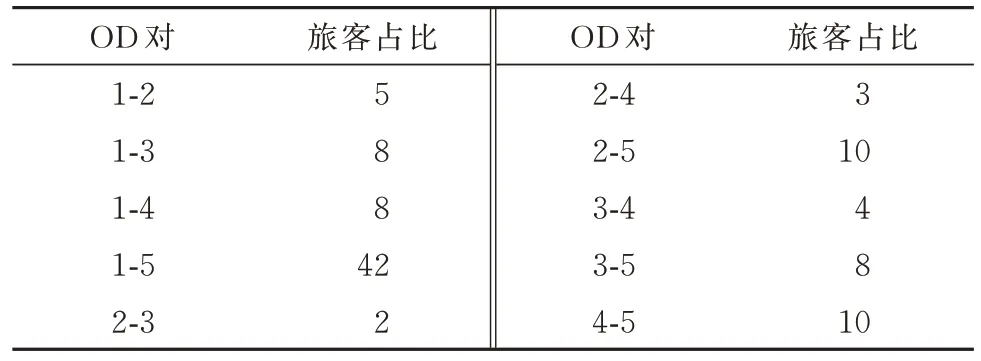
表2 各OD 对客流量比例Tab.2 Percentage of passenger flow in each OD pairs %

假定列车开行方向为成都东到重庆北，分别对应车站编号为1～5，共计10 个OD 对.考虑到人们出行时间和城市各种交通方式相互衔接情况，列车开行时间段设为6：30 到21：30，共900 min，180 个时隙.旅客到达服从泊松分布，时间分布呈双向峰型，分别为早高峰7：00-9：00，晚高峰为17：00-19：00.旅客达到由Monte Carlo 法生成模拟泊松流，每5 min获得一个旅客到达数λ，λ为一个整数变量，在时间上处于渐变状态，以成都东—重庆北为例，旅客到达分布如图3 所示.

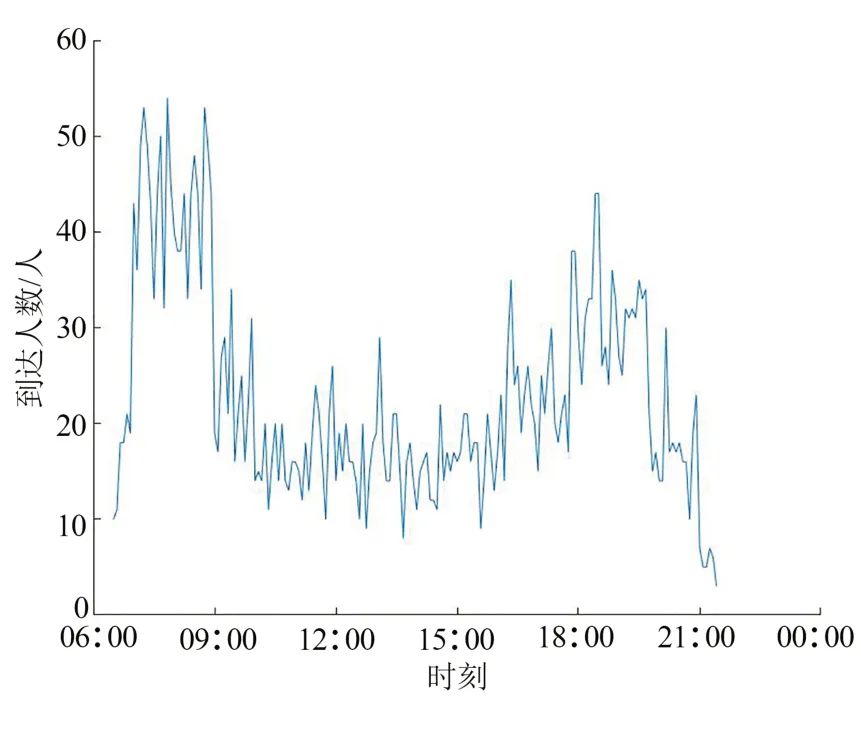
图3 成都东—重庆北各时隙客流到达分布图Fig.3 Distribution map of Chengdu east-Chongqi north passenger flow arrival

假定在列车开行时间6：30 之前，各OD 对旅客排队乘车人数都为0.在当前票价下，列车的开行方案主要取决于客流达到分布和旅客排队人数.根据模拟的旅客到达分布，各OD 对的旅客到达数λ作为各OD 对新增旅客数，依次输入模型，采用Matlab 软件进行求解.在计算过程中，初始选取权重系数V=1 求解，经多次计算取较为稳定的最优解数值，以其中一次计算结果为例，同时选取粒子群算法（Particle Swarm Optimization，PSO）对比IHS 算法，两种算法的效率见图4，由图4 可知IHS 算法收敛速度优于PSO 算法，目标函数结果相差不大，结果可靠.

图4 PSO 算法和IHS 算法效率分析Fig.4 Efficiency analysis of PSO algorithm and IHS algorithm

优化后的开行方案结果为每天开行28 趟车次，较优化前增加8 列，中间停站数也有了一定增加，主要是在非高峰时隙增加了一定车次，旅客出行更加便捷，开行方案见图5.同时，高峰时隙开行车次相对非高峰时隙更为密集，有效地耦合了客流出行需求，能减少旅客排队等待时间.优化后开行方案中有直达列车4 列，所有车站全停列车3 列，其他车次则是停靠3 个或4 个车站，车站2、3、4 停站次数分别为12、16、14 次.

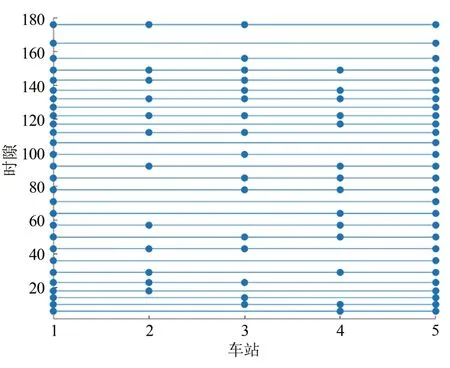
图5 列车开行与停站方案图Fig.5 Schematic diagram of train running and stopping plan

优化前高峰时隙旅客排队队列长度较小，大多数高峰时隙旅客排队人数控制100 人以内；多数非高峰时隙旅客队列较长，旅客到达车站不能及时被运走，队列长度一直增加，部分时隙排队人数超过600 人；由于晚间缺少开行列车，选择该线路1 300多名旅客的出行不能得到满足，运输网络不稳定.优化后整个周期列车开行时间间隔比较均衡，平均每个时隙旅客排队人数在200 人以内，保证了旅客平均到达率小于平均服务率，系统队列长度不会无限增加，运输线路保持稳定.开行方案优化前后各时隙旅客排队人数变化情况见图6，优化后各OD 对旅客平均排队人数见表3.结果表明旅客平均排队人数与两城市的客流量大小呈正相关关系，客流量越大，平均排队人数越多.

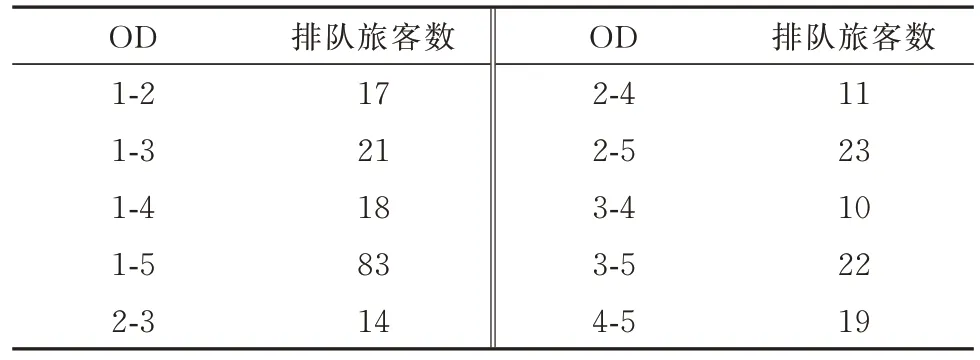
表3 各OD 旅客平均排队人数Tab.3 The average number of passengers in queue for each OD

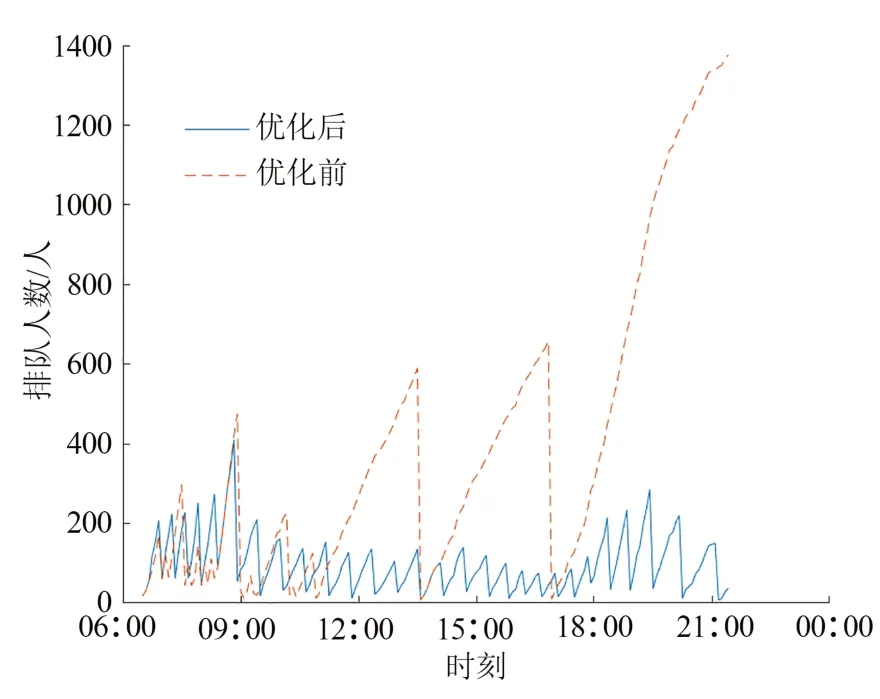
图6 优化前后旅客排队人数图Fig.6 The number of passengers in queue before and after optimization.

根据式（9）计算得到某OD 对旅客平均等待时间，然后进行累加，得到所有OD 对旅客平均等待时间减少约12.1 min，减少比例为28.3%.

对于权重系数V值对优化目标的影响，V分别取值为1、5、10、20、50、100、200、500，计算列车开行成本和旅客排队长度值，结果如图7 所示.当V逐渐増大时，铁路企业的开行成本权重增加，开行成本逐渐收敛到最优值，排队人数也逐渐逼近到最大值.V取17 时，开行成本和排队人数两者比较均衡；当V＞200后，开行成本和旅客排队人数趋于稳定.权重系数V表明在客流到达分布一定的条件下，开行成本存在下界，旅客排队等车人数存在上界，开行成本和旅客等待时间逐渐趋于稳定，与引理2 相符，式（17）可实现开行成本与平均排队长度两者的协同优化.

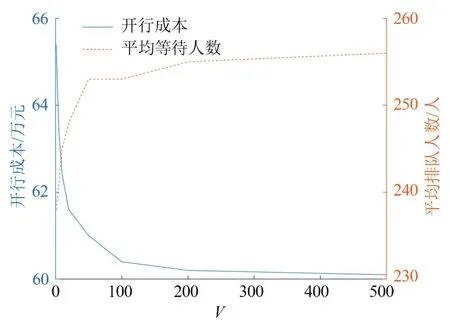
图7 开行成本、排队人数与权重系数V 关系Fig.7 Relationship between operation cost,number of people in queue and weighting factor V

5 结论

针对无须购票的公交化城际列车开行方案优化问题，引入Lyapunov 函数控制旅客乘车排队长度，实现旅客排队等待时间和铁路企业开行成本的协同优化.主要研究结论如下：

1）相比现行开行方案优化模型，Lyapunov 排队长度变化界限模型可以在保证铁路企业成本的情形下，有效控制旅客的乘车排队长度，减少旅客的排队等待时间，满足旅客快速出行，保证运输线路稳定.

2）铁路企业可以根据实际情况，不断调整权重系数平衡双方的利益，V值越大则表示越注重铁路企业开行成本，最终实现双方利益的最优.

3）铁路企业已经获得自主定价权利，可以制定不同票价来吸引旅客出行，而票价又会调节客流量大小，未来可以研究“铁路e 卡通”型城际列车定价与开行方案的协同优化，以方便乘客出行和提升铁路企业收益.