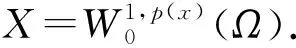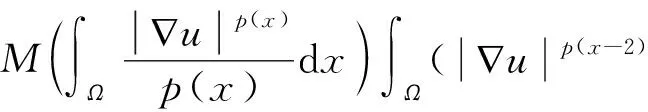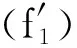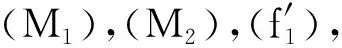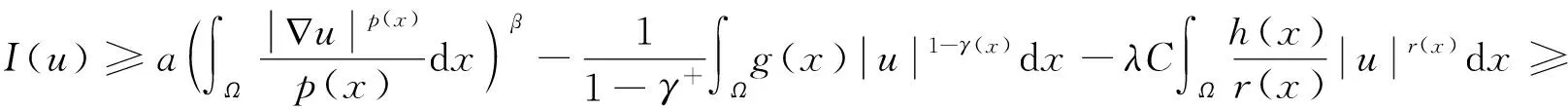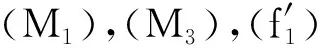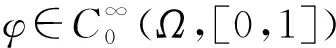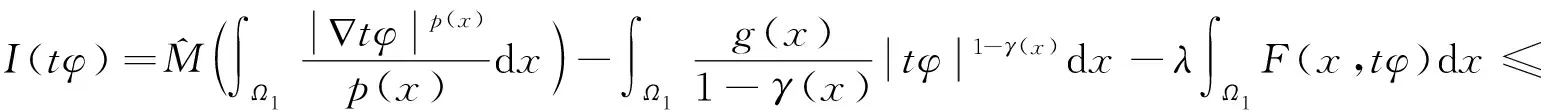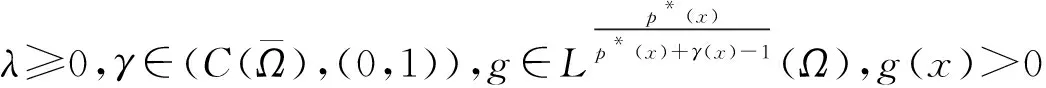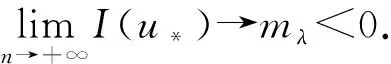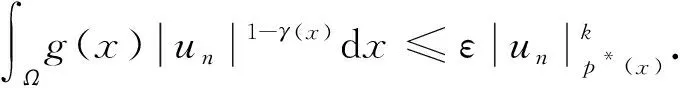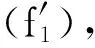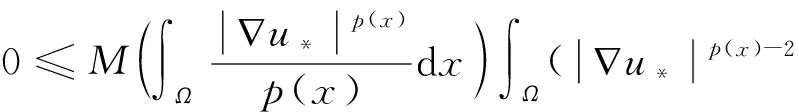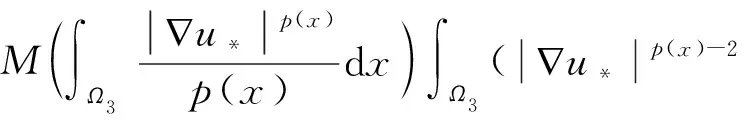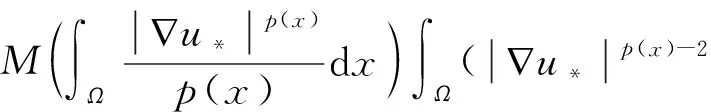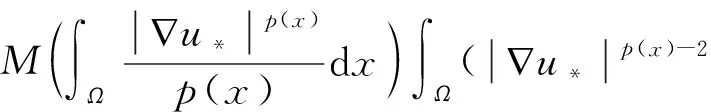一类具有奇异项的p(x)-Kirchhoff方程解的存在性
谢嫣玲,肖宇霞,储昌木
(贵州民族大学数据科学与信息工程学院,贵州 贵阳 550025)
1 引言和主要结果
考虑如下含奇异项的p(x)-Kirchhoff型方程:
(1)
其中:Ω⊂N(N≥3)是具有C2边界的光滑有界域;且满足∇u)是p(x)-Laplace算子;M和f(x,u)为满足一定条件的连续函数;λ是实参数;是连续函数且满足在Ω上几乎处处成立,这里
问题(1)源于如下Kirchhoff模型:
(2)
近年来,由于Kirchhoff模型在电流变流体、图像恢复等方面有重要的应用[1-2],形如问题(1)的非局部椭圆问题受到了人们的广泛关注[3-8].特别地,文献[3]研究了如下问题非平凡弱解的存在性:
(3)
其中:Ω⊂N(N≥3)是有界正则域;a,b≥0,a+b>0;p≥2;0<γ<1;λ≥0;g(x)≥0在Ω上几乎处处成立,且,)满足
(f1) 对任意u∈,有f(x,tu)=f(x,u),
(f2) 存在Ω1⊂⊂Ω,|Ω1|>0,使得f(x,t)≥0,x∈Ω1.
文献[4]运用极小极大方法获得了问题(3)非平凡弱解的存在性.此外,文献[4]假设M满足如下条件:
(M1)M(t)是(0,∞)上的连续函数,M(t)>0,且对任意的T>0,有M(t)∈L1(0,T);
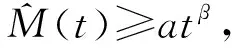
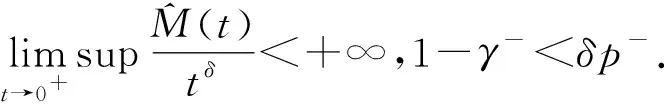
该文研究了问题(1)在λ<0的情形.在f满足一定条件时,利用极小极大方法获得了该类方程非平凡弱解的存在性.
然而,作为问题(3)的更一般情形,对满足上述条件的M(t),当λ>0时,问题(1)的可解性研究尚未发现.本文给出比(f1)更弱的条件:
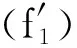
本文的主要结果如下:
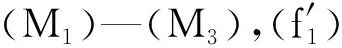
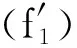
2 预备知识
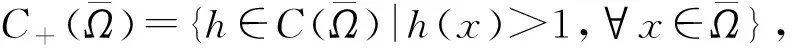
对应的范数分别为
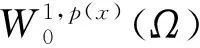
命题1[4]设1 (ⅰ) 若对任意x∈Ω,r(x)≤q(x),则Lq(x)(Ω)→Lr(x)(Ω)是连续的; (ⅱ) 若q(x) (ⅰ) |u|p(x)<1(=1或>1)⟺ρ(u)<1(=1或>1); 命题4[4]设p(x),q(x)是可测函数,对任意的x∈Ω,p(x)∈L∞(Ω),1≤p(x)q(x)≤∞.若u∈Lq(x)(Ω),u≠0,则 (4) 定义1 若对任意x∈Ω,v∈X都有 (5) 则称u∈X为方程(1)的一个弱解. 由于max{1-γ-,r+}<βp-,所以当‖u‖→+∞时,I(u)→+∞.故泛函I在X上是强制的. 由δp->1-γ-和g(x)>0在Ω上几乎处处成立知,存在t*∈(0,1),使得对当t∈(0,t*)时,I(tφ)<0. (6) 由Hölder不等式和命题4可推出 (7) 由Hölder不等式可得 通过Lebesgue控制收敛定理和命题4得 (8) 因此,结合(6),(7),(8)式可知泛函I是弱下半连续的,且满足 即I(u*)=mλ<0. 定理1的证明由引理3可知,u*是泛函I的局部极小点,I(u*)=mλ<0,这意味着u*≠0.下证u*是问题(1)的一个弱解. 设φ∈X,0<ε<1,定义Ψ=(u*+εφ)+∈X,其中Ψ=(u*+εφ)+=max{u*+εφ,0},记Ω3={x|u*+εφ≤0},Ω4={x|u*+εφ>0}.因为u*是泛函I的局部极小点,则有 当ε→0+时,Ω3={x|u*+εφ≤0}积分区域是可测的,对任意的φ∈X,故有 由ε→0+,得到 用-φ替换φ,可得到相反的不等式.因此, 故u*是问题(1)的一个弱解.从而u*是问题(1)的一个非平凡弱解.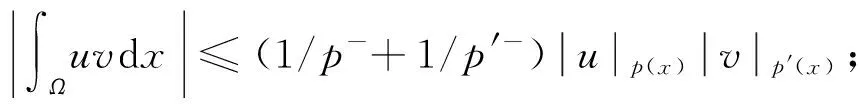
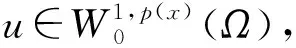
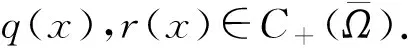
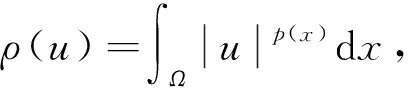
3 主要结果的证明