融合压缩采样与深度神经网络的直接序列扩频参数估计*
刘 锋,张 爽,黄渝昂
(南开大学 a.电子信息与光学工程学院;b.天津市光电传感器与传感网络技术实验室,天津300350)
0 引 言
直接序列扩频(Direct sequence spread spectrum,DSSS)已成为了现代无线通信领域中主要的扩频技术之一。在DSSS中,基带数字信号通过高速率的伪随机序列,被调制到更宽的频带上。由于频带的展宽,DSSS信号一般具有较低的功率谱密度,并且其频带位置不易被感知。因此,DSSS信号被广泛地应用于军事领域,例如军用战术移动通信电台、导航以及航空测绘等。
接收端对DSSS信号的处理主要包括信号检测、参数估计、扩频码及基带信号恢复等。其中,参数估计是后续信号信息恢复的前提条件[1]。针对DSSS信号的估计,研究者提出了很多种方法。然而,现有方法普遍是基于奈奎斯特采样定理和信号的自相关性质,随着扩频信号的带宽不断增加,现有方法逐渐面临采样速率上的瓶颈。
压缩采样理论[2-3]可以有效解决扩频信号高宽带特性带来的高采样率和海量数据处理问题[4-5]。压缩采样理论指出,如果信号是稀疏的或者在某个变换下是可以进行稀疏表示的,那么通过低于奈奎斯特定理要求的采样速率所获得的信号测量结果,依然可对信号信息进行重构。针对DSSS信号的非合作接收,研究者基于压缩采样理论进行了一系列的研究。然而,现有方法大都需要对压缩采样数据进行信号的重构,而重构算法计算复杂,很难对扩频信号进行在线处理。
随着计算机技术的突飞猛进,深度学习[6]被广泛应用于计算机视觉、语音识别、自然语言处理等多种领域。深度学习是一种以人工神经网络为架构,对数据进行表征学习的算法[7]。经过充分训练的神经网络对输入数据具有很好的特征提取与分析能力,并且具有高效的在线处理能力。由于这一优势,越来越多的研究者将各种信号处理与深度学习相结合[8]。然而,现有的基于深度学习的信号特征与参数提取方法大多针对非下采样信号,对于超宽带不易采用奈奎斯特采样的情况,此类方法还有待进一步研究。
针对现有方法的不足,本文融合压缩采样和深度神经网络理论,以码片周期与码元周期参数估计为例,提出了DSSS信号参数估计的新方法:首先通过神经网络中首层卷积层的线性运算和下采样对DSSS信号进行压缩采样设计,而后使用残差模块部分对压缩采样数据进行特征提取,最后神经网络中的全连接层对提取到的信息进行整合,得到参数估计结果。本文所提出方法具有以下的创新性:一方面,压缩采样能够利用信号冗余性,降低DSSS信号的采样成本;另一方面,深度神经网络能够在线高效且准确地提取压缩采样数据中信号的参数特征。本文将压缩采样机制与参数估计网络的设计同时进行,两者高度融合,进而保证了所提出方法在参数估计上的有效性。仿真实验表明,本文所提方法在参数估计上具有很好的准确性。
1 直接序列扩频通信原理
1.1 DSSS信号模型
本文以DSSS信号的码片周期以及码元周期两个参数的估计为例,进行参数估计方法的研究。本文将扩频码序列调制后的直接序列扩频信号作为研究目标,其可表示为
s(t)=Am(t)h(t) 。
(1)
式中:A表示信号的幅值;m(t)是信息序列波形,h(t)是扩频码序列波形,并且有
(2)
(3)
式中:mi是信息码并且有mi∈{-1,+1},Td是信号的码元周期,p(t)是矩形脉冲,hj∈{-1,+1}是扩频码,Tc是信号的码片周期。
1.2 扩频码序列
用于DSSS信号调制的扩频码序列通常是伪随机码,又称为伪噪声(Pseudo Noise,PN)码。PN码具有和白噪声相似的特性,其功率谱在频带中均匀分布。常用的PN码有m序列、Kasami序列、Gold序列等。在这些序列中,m序列也可以用来构造其他的序列,因此使用最多。m序列发生器由r级移位寄存器组成,其原理如图1所示。其中,ai(i=0,1,2,…,n)是每位寄存器的状态(0或1),由随机初始化决定;ci(i=0,1,2,…,n)是反馈系数,由本原多项式的系数决定。图中的加法均为二进制加法。本文以1~5阶m序列为例进行DSSS信号数据集的构建,其本原多项式如表1所示。
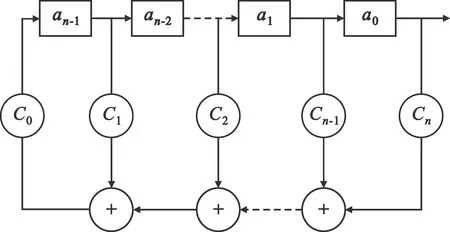
图1 m序列发生器的产生原理

表1 1~5阶m序列的本原多项式
基于调制后的DSSS信号生成了用于神经网络训练的数据集。
2 DSSS信号参数估计算法结构
2.1 参数估计算法结构
针对DSSS信号码片周期、码元周期参数的估计,本文采用图2所示的算法结构。该算法首先利用输入滤波器滤去输入DSSS信号观测频带以外的噪声;其次,滤波器与采样器协同工作,采样器以较低的频率工作,实现对DSSS信号的压缩采样;最后,参数估计网络利用压缩采样数据,实现对DSSS信号码片周期、码元周期参数的估计。

图2 DSSS信号参数估计的算法结构
2.2 参数估计的设计方法
本文基于深度神经网络的训练,同时设计压缩采样与参数估计网络。
在深度学习中,存在着一种网络退化现象,即随着深度学习网络深度的加深,模型的准确度会逐渐趋于饱和甚至会开始降低,更直观的是层数越多的神经网络,模型的训练难度会越来越高。残差神经网络的提出可以有效地避免退化现象。受残差模块的启发,本文基于残差模块搭建用于DSSS信号参数估计的网络结构,其中残差模块的基本结构如图3(a)所示。在图3(a)中,1×3表示卷积核尺寸,N表示卷积核个数。
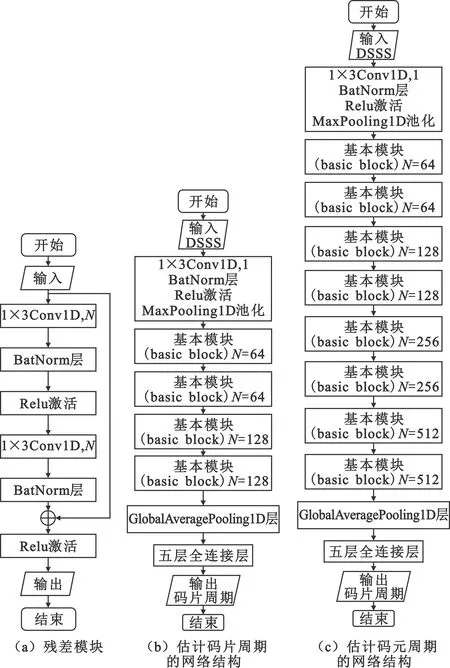
图3 估计DSSS参数的网络结构
本文用一个神经网络结构,同时实现对DSSS信号压缩采样与参数估计两部分的设计与训练优化,进而使得这两部分能够高度融合,增加参数估计的准确性。输入的DSSS信号通过首层一维卷积层的线性运算与下采样操作,即图2中的线性滤波器与下采样模块,实现压缩采样:将首层一维卷积层的卷积核作为线性滤波器的冲激响应,同时通过调整该卷积层的移动步长,进而调整下采样间隔与压缩采样的压缩比,而神经网络的其余部分则被用于对压缩后的数据进行参数估计。图3(b)和图3(c)分别是估计码片周期和码元周期的网络结构,Conv1D表示首层一维卷积层,用来实现对输入信号的压缩采样;基本模块即图3(a)所表示的残差模块基本结构,用于提取压缩采样数据的信号特征;五层全连接的节点数分别是125、512、125、62、1。利用全连接层进行数据特征的整合,输出信号参数的估计结果。
3 数据集的产生与神经网络的训练
3.1 数据集的产生
本文所提出的方法以人工神经网络的训练为基础,而人工神经网络的训练需要一个数据量比较大的数据集。本文样本数据集的产生流程如图4所示。

图4 样本数据集生成流程图
如图4所示,首先随机产生(-1,+1)的基带信号;接着,按照表1所给出的1~5阶PN序列的本原多项式,依次生成234种PN序列;然后,针对生成的PN序列进行采样,对每个码片的采样数目至少为两次(PN序列每个码片的采样数即为码片周期,在数据集的构建中将这一数值作为真实标签并进一步保存;为方便数据集的构造与神经网络的研究,本文中的采样数设置为2、3、4,实际中的采样数也可以为其他不同的数值);最后,利用采样后的PN序列进行基带信号的调制。由于不同阶的PN序列长度以及每个码片的采样数目不同,最终产生的信号长度也不同。为了保证输入神经网络的数据尺寸相同,本文取每个调制信号的前N个样本(N=600)生成数据集。在生成每一个样本数据的同时,其码片周期、码元周期标签会被相应地建立。
3.2 神经网络的训练
本文基于TensorFlow 2.0 (GPU)进行人工神经网络的训练,对应的python版本是python3.7,实验的电脑CPU为Intel Core i5-9400@2.90 GHz,RAM大小为32.0 GB。利用3.1所述方法,共产生了167 760个数据,并使用train_test_split划分数据集的方法,将其中的80%作为训练集,20%作为测试集。神经网络每一个训练批次的数据为256。在神经网络的训练过程中,往数据集中加入一定的噪声,使得信号的带内信噪比(即图2中经过预滤波之后的信噪比)为0 dB。信号带内信噪比(Signal-to-Noise Ratio,SNR)的表达式为
(4)

本文中的神经网络训练过程采用Adadelta优化器,并且使用初始学习率为0.2的指数衰减形式的动态学习率。在神经网络的训练过程中,选取网络的最终输出结果与真实标签的均方误差(Mean Square Error,MSE)作为网络的训练损失函数,表达式为
(5)

4 仿真与分析
4.1 DSSS信号码片周期的估计结果
在估计码片周期的神经网络中,输入600长度的DSSS信号,首先经过一维卷积层中的线性卷积与下采样操作。该卷积层中卷积核个数设为1,卷积核大小设为3。在图2的参数估计算法结构中,通过线性滤波器与采样器可以实现压缩采样:在神经网络结构中,本文将神经网络首层卷积核的训练结果作为线性滤波器的冲激响应;调整卷积层中的步长进而调整卷积层下采样的结果,从而实现不同的压缩比。本文中的步长设为2,使得信号被压缩成300长度,即压缩比为2;而后参数估计网络基于压缩后的数据进行码片周期的估计。本文将网络输出结果和真实值之间的均方误差作为损失函数,输出结果是否等于真实值作为准确率指标,对网络进行了100个epoch(一个epoch表示所有的训练数据训练一次)的训练后,训练集的损失曲线、测试集的准确率曲线分别如图5(a)和图5(b)所示。图中,Loss为网络训练的损失函数,ACC为网络输出结果与真实值之间的准确率。从图中可以看出,估计码片周期的神经网络取得了很好的训练结果。最终,训练数据的损失达到了0.000 9,测试集的准确率达到了99.68%。
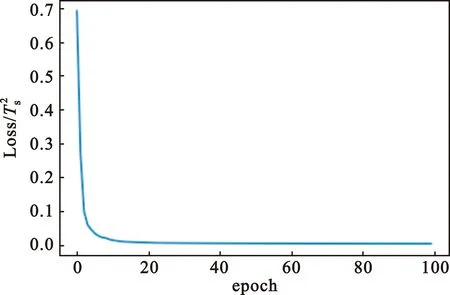
(a)训练集损失曲线

(a)本文方法
4.2 DSSS信号码元周期的估计结果
与估计码片周期的原理相同,输入600长度的信号首先经过一维卷积进行下采样操作,参数估计网络基于压缩采样数据进行码元周期参数的估计。本文对网络进行了350个epoch的训练后,训练集的损失曲线、测试集的准确率曲线分别如图7(a)和图7(b)所示。与4.1节中估计码片周期的网络结果相同,估计码元周期的网络也取得了很好的效果:训练数据的损失最终达到了0.04,测试集的准确率达到了94.51%。
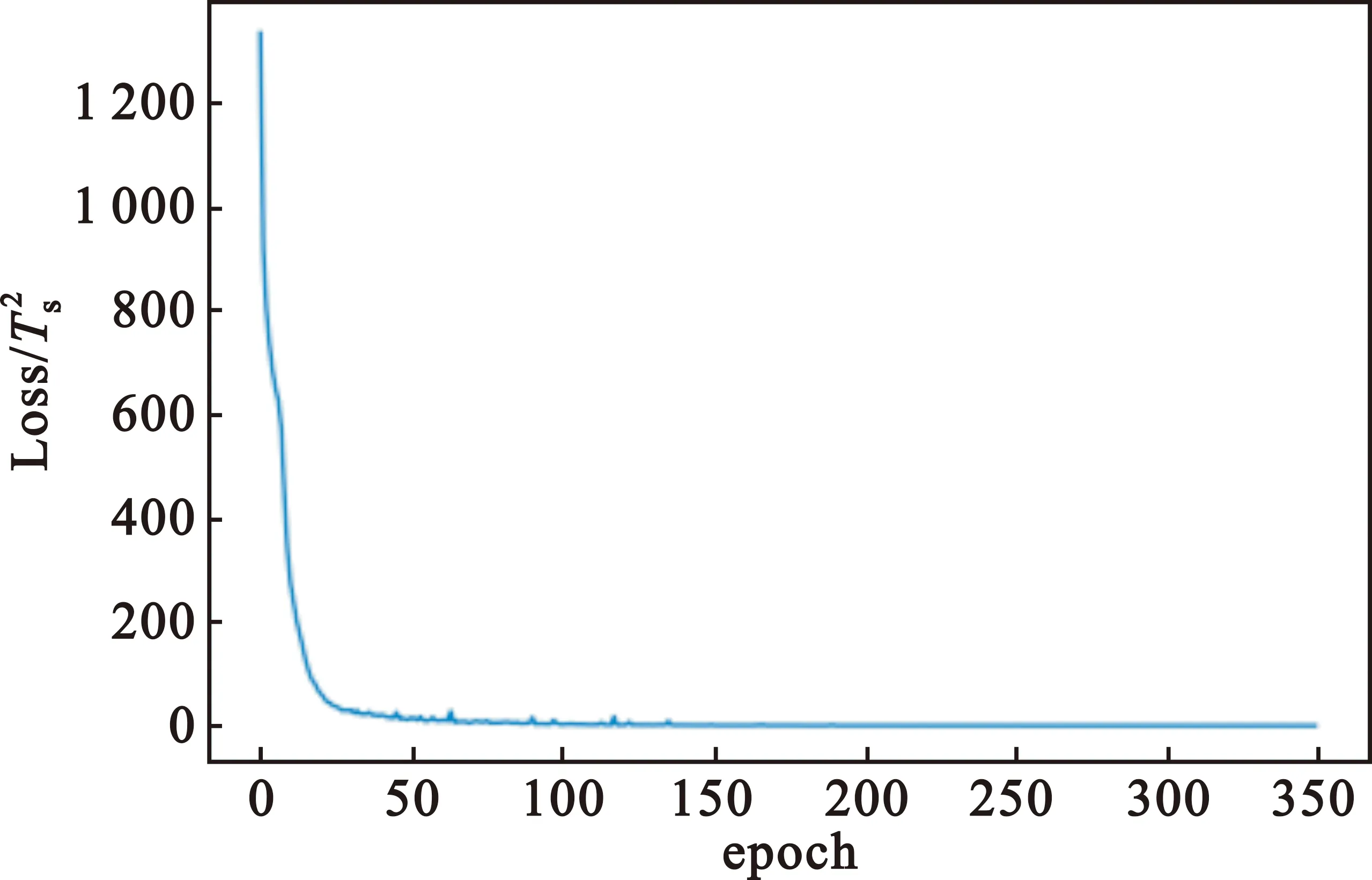
(a)训练集损失曲线
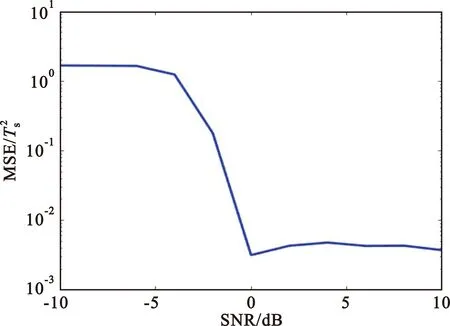
与码片周期估计相同,也采用27 960个数据对估计码元周期的网络进行验证,仿真曲线如图8(a)所示。与码片周期估计结果相同,码元周期的估计结果与真实值之间的误差随着信噪比的增加而下降。

(a)本文方法
5 结束语
本文主要基于压缩采样和人工神经网络对直接序列扩频信号中的参数进行估计,基于残差模块搭建了用于DSSS信号码片周期与码元周期参数估计的神经网络。利用神经网络的首层卷积线性运算与下采样操作,实现压缩采样模块的设计,同时利用网络其余的部分,实现基于压缩采样数据的信号参数估计。经过实验仿真验证,神经网络的训练损失曲线以及准确率曲线均取得了很好的效果。相对于传统方法在低信噪比情况下不具备估计能力的状况,本文方法具有一定的提升。
随着神经网络的设计与训练,本文信号参数估计的效果得到了显著提升。但从实时性角度出发,基于神经网络的训练需要大量的训练数据作为支撑,因此对其时效性的相关改进是今后研究的重要方向。

