基于用户分簇的认知超密集网络资源分配*
张俊杰,仇润鹤
(1.东华大学 信息科学与技术学院,上海 201620;2.数字化纺织服装技术教育部工程研究中心,上海 201620)
0 引 言
超密集网络[1](Ultra-dense Network,UDN)是5G时代提升网络容量的有效技术,通过增加低功率的微微毫基站(Femtocell Base Station,FBS)的部署密度,使用适合短距离传输的毫米波频段,减小了建筑遮挡造成的阴影效应,以及长距离传输等造成的信号衰弱。相比宏基站(Macro Base Station,MBS)的大覆盖,密集部署的FBS能实现更高的吞吐量。认知无线电[2](Cognitive Radio,CR)是一种提高频谱利用率的技术,利用其频谱感知和分配的功能,可使次用户(Secondary User,SU)在不影响主用户(Primary User,PU)服务质量的前提下,接入信道状态良好的授权信道。
然而FBS部署的随机性使得小区间干扰严重。将认知技术引入超密集网络,能为SU提供额外的信道状态良好的授权频段,提高SU吞吐量。文献[3-14]对CR-UDN模型展开了研究,但主要讨论异构网络下跨层干扰问题,而同构网络下的干扰图构建始终存在一个阈值选取问题。且当用户密度、基站密度都较大时,已有的干扰图构建方法,即基站与基站或用户与用户之间的路径损耗不能准确反映两用户间的干扰情况。
本文在CR-UDN模型下提出一种改进的基于用户分簇的资源分配方案:基于基站的覆盖范围,选出每个用户的强干扰基站,建立用户-用户干扰图,以用户受到的平均弱干扰划分优先级对用户分簇,再为簇集群预分配频段,为每个簇分配对应频段中效用最大的信道,实现次用户吞吐量的最大化。
1 网络模型与问题描述
1.1 网络模型
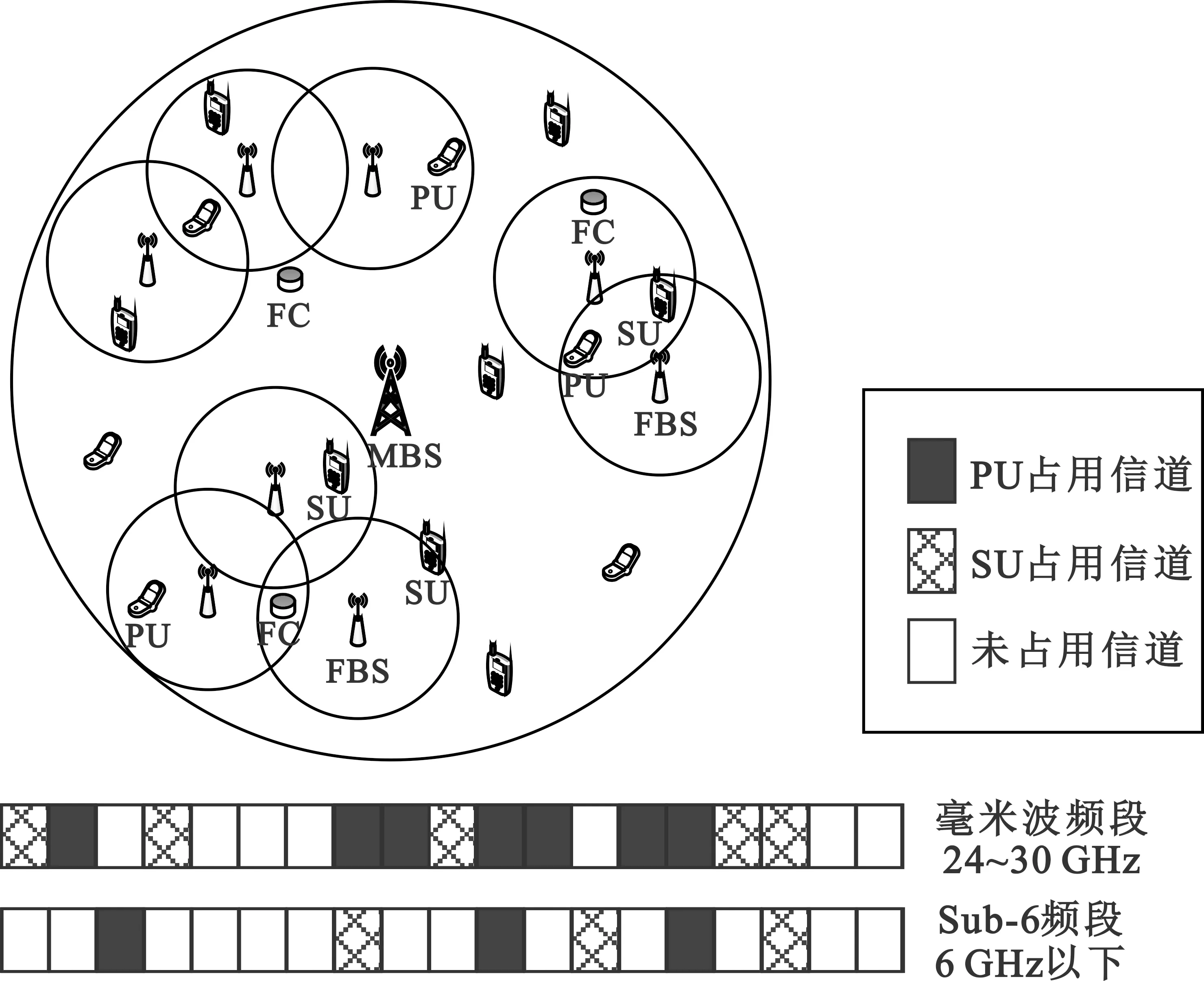
图1 认知超密集网络模型
用户n的信干噪比rn可表示为
(1)
式中:gk,n,m为一个三维的01向量,gk,n,m=1 时表示用户n使用信道m与基站k通信,gk,n,m=0则表示没有该连接关系;gk′,n,m为基站k′对用户n的干扰增益;Pk,n,m为基站k使用信道m为用户n分配的发射功率;hk,n,m为基站k在信道m上到用户n的信道增益;N0为高斯白噪声。信道增益可表示为如下向量:
(2)
式中:dk,n为基站k到用户n的距离,dk,n上的系数为-6~-2,具体取值与环境有关;Gk,n,m为无线信道的小尺度衰弱,对于不同的k、n、m是独立的同分布复高斯随机变换,具有零均值和单位方差。根据香农公式,当载波间隔为W时,网络总吞吐量可表示为
(3)
1.2 问题描述
本文的目标为对认知超密集同构网络进行干扰减轻的资源分配,最大化网络中次用户的总吞吐量。优化问题如下:
(4a)
(4b)
(4c)
(4d)
(4e)
(4f)
C6:gk,n,m=[0,1] 。
(4g)
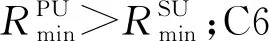
优化问题(4a)~(4f)是一个三维非线性混合整数规划问题,本文提出一种改进的基于用户分簇的资源分配方案,以较低的复杂度为用户进行干扰减轻的资源分配。
2 基于用户分簇的资源分配
由于已有的资源分配算法对用户基站密度均较高的模型没有很好的适用性,本文提出一种改进的基于用户分簇的资源分配算法,思路如下:
(1)基于基站覆盖范围建立干扰图,划分强弱干扰;
(2)按照平均弱干扰划分用户分簇的优先级;
(3)将待分配信道分段,每个子段独立分配信道,降低资源分配的复杂度。
2.1 基于基站覆盖范围构建干扰图
建立干扰图为信道分配做准备工作。一般图着色建立干扰图的方法是,比较用户与用户之间的路径损耗或受到周围基站的干扰总和,超过某一阈值时认为两用户间存在边,即两用户存在干扰。然而阈值却需要人为选取,且仅适用于用户基站密度均较低的模型。本文提出一种基于基站覆盖范围的干扰图构建方法。受文献[15]以用户为中心的网络选择干扰基站群的启发,本文为每个用户选择强干扰基站。
强干扰基站的选择方法如下:首先以用户为圆心,以基站覆盖半径为半径的圆域内包含的基站称为该用户的强干扰基站,如图2所示。当用户n1的强干扰基站与用户n2的服务基站存在交集时,认为用户n2对n1存在强干扰,同一FBS服务的用户间均存在强干扰,存在强干扰的用户将不会分到同一信道。同时生成一个N×N的矩阵β,当用户n2对n1存在强干扰,令β(n1,n2)=1,否则β(n1,n2)=0。

图2 强弱干扰划分示意图

(5)
2.2 认知模型下划分优先级的用户分簇
用户分簇目的是将用户间干扰小的基站分为一簇。为保障分簇的公平性,我们对用户进行优先级划分,受到平均干扰高的用户将优先分簇和优先选择簇成员。
由于存在强干扰的用户不会被分到同一簇中,在计算用户受到的平均干扰时,仅考虑非强干扰用户(我们称其为弱干扰用户)造成的弱干扰,如图2所示。平均弱干扰Theta的计算方法(算法1)如下:
Step2IN(n1,n2)=IN(n2,n1)=max(In(n1,n2),In(n2,n1))。
Step3β′=E-β。
Step4 theta=β′·IN。
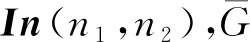
(6)
由于两用户间的干扰具有不对称性,Step 2逐个取矩阵In与In转置的最大值,更新后的矩阵为IN。
Step 3构造弱干扰01关系阵β′,当n2对n1存在弱干扰,令β′(n1,n2)=1,其中,E为N×N的单位矩阵,β为强干扰01关系阵。
Step 4筛选用户的弱干扰系数阵theta,式中使用矩阵点乘。
Step 5求用户n的平均弱干扰Thetan。δ(x)为一布尔函数,当事件x为真,δ(x)=1,否则为0。
将所有SU按Theta降序排列,得到SU分簇的优先级排列I。尽管进行了SU的优先级排列,但在信道分配阶段仍以个体的最大效用进行资源分配。为使SU吞吐量最大化,对所有PU和SU进行二次优先级排列,并按照信道资源可能的占用情况将所有簇划分为四个部分,如图3所示。

图3 簇集群划分示意图
用户分簇算法(算法2)如下:
Step1 按序从I中剩余成员抽取一个SU。
Step2 将该SU存入新的簇中,当前簇为gl。

将用户I(s)存入簇中,并将I(s)从I中除去。
Step4 重复执行Step 3,当簇成员数达到Cmax时,或I中剩余SU均与gl内存在强干扰,该簇分配结束。其中Cmax为一变量,取值如下:
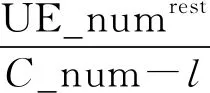
(7)
式中:UE_numrest为未分簇的用户数量,C_num为总信道数,l为已分配簇的个数,⎣」为向下取整。安排图3的分簇顺序可以使优先级靠前的簇内用户优先分配到簇内干扰小的簇成员;设置动态的簇成员上限Cmax可避免信道分配阶段空余信道的出现,且在用户数量较少时避免同频干扰的出现。
用户分簇的步骤如下:
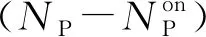
Step2 循环执行算法2对I中剩余的SU分簇。当分簇个数等于NS时,停止循环,已分配簇集群归入L2。
Step3 将每个在线的PU分至独立的簇中,一共MP个簇。对每个簇执行算法2中的Step 3和Step 4,已分配簇集群归入L3。
Step4 循环执行算法2对I中剩余的SU分簇,直到I为空集,已分配簇集群归入L4。
2.3 认知模型下的信道分配

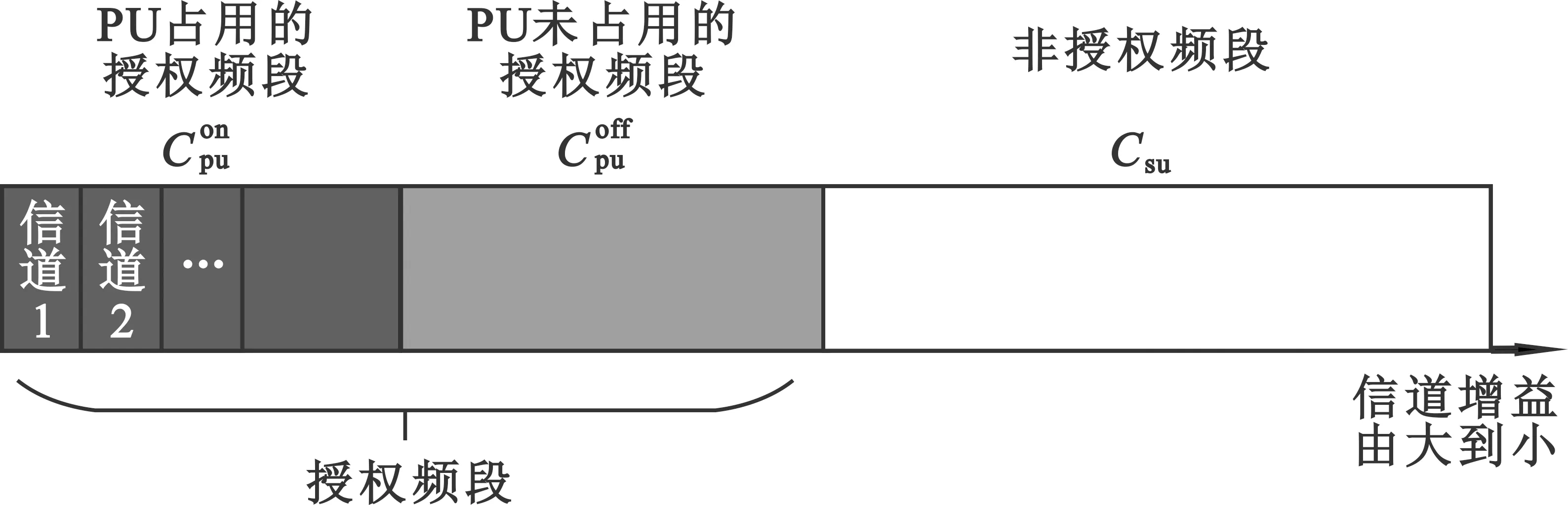
图4 频段划分示意图
假设认知FBS可完美感知信道信息,且可按照小尺度衰弱对信道排序。本文模拟PU已占用授权信道后SU接入的过程,为避免纯SU簇使用PU已占用信道,优先为PU簇分配信道。

Step1 遍历Li中所有簇,i=1,2,3。
Step2 IfC≠∅,C为Li对应频段中的剩余信道,C(m)=arg max(RLi(j),m),RLi(j),m为分配到信道m时簇集群Li中第j个簇内的用户吞吐量之和。
Step3 将信道m分配给簇Li(j)内所有成员。
Step4C=C/C(m)。
由于信道数量有限,当信道数量大于等于分簇数量时,可按以上算法分配;当信道数量小于分簇数量,即出现L4簇集群时,遍历已分配信道的簇成员,将L4中的SU分至没有强干扰的用户簇中,并共享该用户簇使用的信道。本文资源分配的框架如图5所示。

图5 基于用户分簇的资源分配算法框架
3 复杂度分析
建立干扰图阶段:每个用户需遍历FBS寻找强干扰基站,复杂度为N(K-1);确认β,比较用户之间备选基站的交集,复杂度为N(N-1)K′,K′为用户备选基站数;对所有用户干扰度排序,复杂度为O(N)。

由上述分析可以见,本文算法复杂度与用户个数、FBS个数、信道总数均呈正比关系。在复杂度较高的信道分配阶段,文献[12]没有执行用户分簇,在信道分配阶段的复杂度为NM;文献[13]在信道分配阶段的复杂度为(M2+M)/2,但没有考虑信道数量不足时的情况;本文进行了分段处理,降低了搜寻最优信道的复杂度。
4 仿真分析
本节将对本文提出算法与IDRAA算法[12]和ILUCA算法[13]进行实验分析,并对比仿真结果。
仿真中考虑单融合中心下FBS用户的资源分配。FBS与用户在100 m×100 m的区域内高密度分布,FBS按照齐次泊松点过程在固定半径的圆域内分布,FBS覆盖范围外的用户由MBS服务,故仿真中的用户仅在随机FBS的覆盖范围内按照齐次泊松点过程分布。忽略跨层干扰,用户与基站的分布如图6所示。
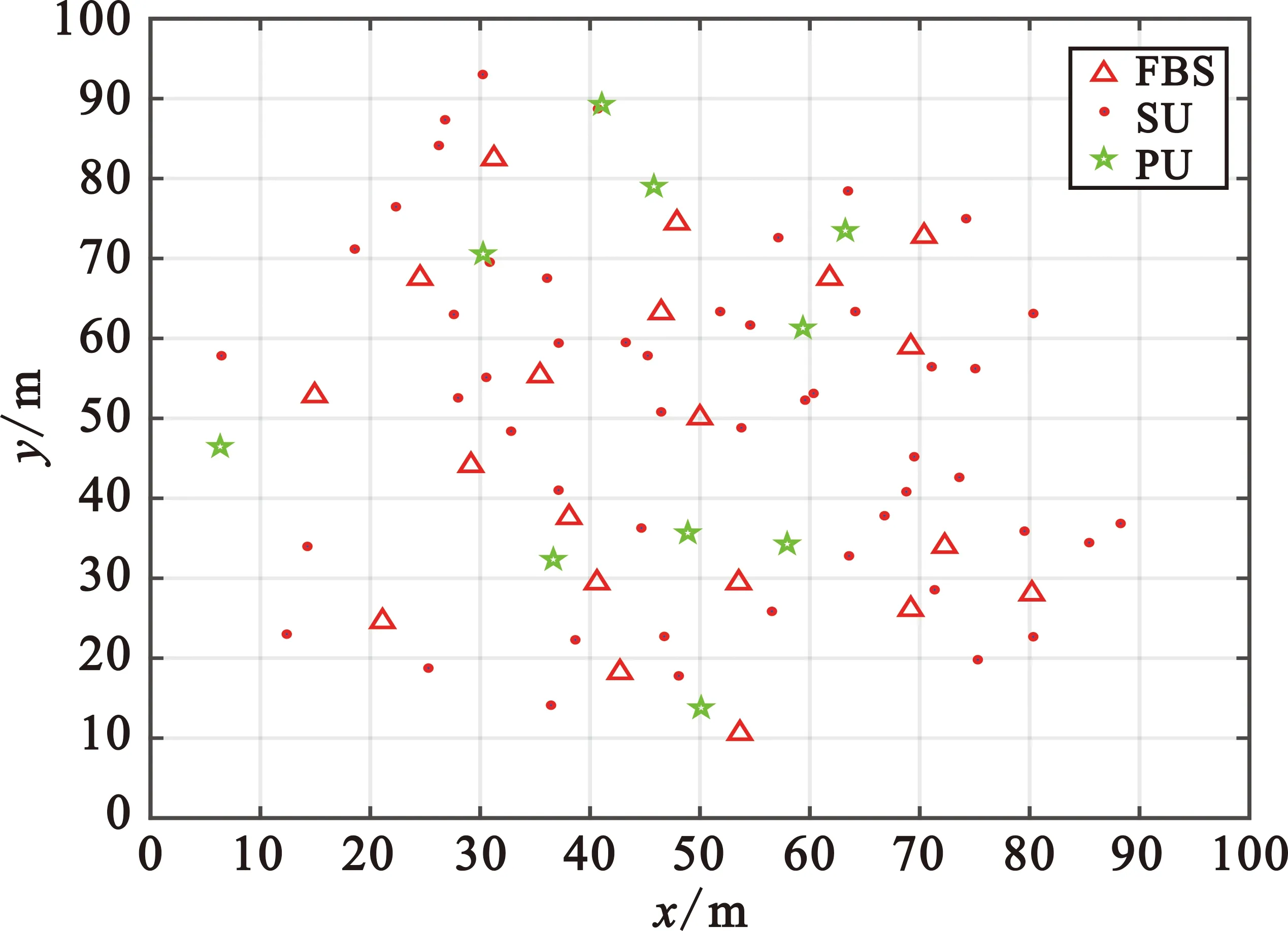
图6 FBS、PU与SU的分布图
FBS为开放式接入,即主次用户均可以接入,并假设认知FBS完美感知主用户的存在情况。本文采用01规划进行用户-基站关系的确立,约束每个用户只能连接一个基站,限制基站的连接上限。
仿真中默认设置20个FBS,40个SU,5个在线PU,10条授权信道,10条非授权信道,一个FC;假设FBS完美感知信道状态,重复试验1 000次。为使结果更具公平性,在更改PU数量时不重新生成新的坐标,而从所有PU(10个)中随机选择在线数量的PU坐标代入试验。参考文献[12-13],仿真参数如表1所示。

表1 仿真参数
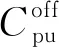
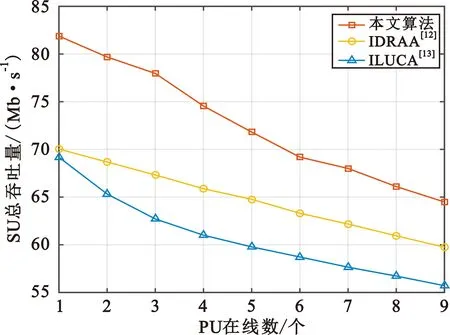
图7 SU总吞吐量随PU在线数的变化


图8 频谱效率随SU接入数的变化
SU总吞吐量与FBS分布密度关系如图9所示。仿真中用户仅分布在FBS的覆盖范围内,当基站分布密度较低时,基站间距较远,同一基站下用户不复用同一信道,同频干扰较小;当基站分布密度提高时,FBS间距缩短,同频干扰增加,吞吐量降低,当基站数量增至区域内基本形成全覆盖时,吞吐量降至谷底,此时基站密度继续增加,开始大量出现基站覆盖范围的重叠,用户有机会选择距离更近的基站接入,有用增益提高,用户吞吐量增加。基站密度的增加过程如图10所示。

图9 SU总吞吐量随FBS分布密度的变化

图10 基站分布密度增加示意图
通过分析CR-UDN模型中PU在线数、SU数量和区域内基站数对SU总吞吐量的影响,与ILUCA和IDRAA算法对比,本文算法在SU总吞吐量和频谱效率的表现上要优于其他两种算法。
5 结束语
本文针对下行CR-UDN中同构网络下的资源分配,提出了一种改进的基于用户分簇的资源分配算法,借助基站的覆盖半径避开了ILUCA建立干扰图时的阈值选择问题,额外考虑了资源分配时的公平性问题。相比IDRAA算法,本文通过用户分簇降低了资源分配的复杂度。仿真结果表明,对比ILUCA和IDRAA算法,在基站密度,用户密度都较高的情况下,本文算法有更好的抗干扰性能,对提高次用户吞吐量方面有更好的表现。但本文没有考虑实际应用场景中认知无线电的非完美感知问题,下一步工作将研究不完美感知CR-UDN模型下的功率分配,并权衡其能效与谱效。

