超宽带系统中基于稀疏恢复的TOA和DOA联合估计方法*

韦 磊,蒋承伶,郭雅娟,徐江涛

(1.国网江苏省电力有限公司，南京 210000；2.国网江苏省电力有限公司电力科学研究院，南京 210008)

0 引 言

目前，在超宽带通信系统中，到达时间(Time of Arrival,TOA)和波达方向(Direction of Arrival,DOA)的估计是一个热点问题[1]。TOA和DOA联合估计方法是从TOA中提取出DOA估计，由于超宽带信号的高时效性，可以获得较高精度的DOA估计。

压缩感知(Compressed Sensing,CS)是文献[2-3]中引入的一种新理论，它将信号感知和压缩统一到单个任务中，利用非线性重构算法从一组随机线性投影中恢复出具有高概率的稀疏信号。除了信号重建和恢复[2-3]外，CS框架还被应用于UWB通信系统中，用于信号检测、信道估计和TOA估计[4-8]。本文提出了一种基于双天线联合稀疏表示框架的红外超宽带信号TOA和DOA联合估计算法。将信号进行频域变换后，在稀疏表示框架中考虑TOA与DOA联合估计问题。利用这一原理，首先采用联合正交匹配追踪(Joint Orthogonal Matching Pursuit,JOMP)算法对两副天线的到达时延进行估计，然后根据两副天线的到达时延的差值来估计DOA参数。该算法能获得自动匹配的TOA和DOA参数，无需信源数已知这一先验条件就能有效获取高精度的TOA和DOA估计结果，且只需较粗略的网格。与借助旋转不变性的信号参数估计技术(Estimating Signal Parameters via Rotational Invariance Techniques,ESPRIT)算法、传统的PM算法和矩阵束(Matrix Pencil,MP)算法相比，本文所提算法具有更好的参数估计性能。

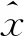
2 信号模型

假设超宽带系统中的发射信号为高斯脉冲信号的二阶导数，并设每个发射信号都是通过直接序列二进制相移键控(Direct Sequence Binary Phase Shift Keying，DS-BPSK)调制的短脉冲重复实现的，则超宽带系统发射的传输信号的表达式如下：

(1)

式中：bj∈{-1,+1}和cn∈{-1,+1}分别表示被调制的二进制数据符号序列和伪随机序列，该序列可以实现多址通信；Tc是脉冲信号的重复周期；Ts是二进制数据符号的周期；Nc表示单个二进制数据符号的脉冲重复次数；p(t)是脉冲波形，由高斯脉冲的二阶导数得到，

(2)

式中：Γ表示脉冲形成因子，主要由脉冲宽度决定。

考虑到一般情况下超宽带信号会通过多径信道传输，根据SV(Saleh-Valenzuela)模型，假设在多径信道下，系统中发射信号的一个脉冲会变为多个多径分量，且在接收阵列接收信号时这些分量会聚集为簇。现假设发射信号在通过多径信道后产生K个簇，L个多径包含在每一簇中，在超宽带信道中，第k簇的信道冲激响应模型表示如下：

(3)

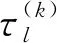
令

βl(k)=αl(k)ejθl(k)

(4)

表示复数衰落的随机幅度，则式(3)可简化为

(5)

第k簇中阵列接收到的信号的时域形式可以根据发射信号s(t)和k簇信道冲激响应h(k)(t)的卷积得到。根据式(1)和式(5)可得

y(k)(t)=s(t)*h(k)(t)+w(k)(t)=

(6)

式中：“*”为卷积运算符号，w(k)(t)为第k簇信号的加性高斯白噪声。转换上式成频域形式可得

Y(k)(ω)=S(ω)H(k)(ω)+W(k)(ω)=

(7)

式中：Y(k)(ω)、S(ω)、H(k)(ω)、W(k)(ω)分别表示y(k)(t)、s(t)、h(k)(t)、w(k)(t)的傅里叶变换。

对频域接收信号在频域等间隔采样，采样点数为N(N>L)，采样间隔为Δω=2π/N，将超宽带信号采样为多个子带进行依次处理。接收信号采样后，离散信号的频域表达式为

Y(k)(ωn)=S(ωn)H(k)(ωn)+W(k)(ωn)=

(8)

式中：ωn=nΔω,n=0,1,…,N-1。上式可以简化为以下向量形式：

yk=SEτβk+wk。

(9)

式中：yk=[Y(k)(ω0),Y(k)(ω1),…,Y(k)(ωN-1)]T∈N×1表示接收信号y(k)(t)的N点频域等间隔采样；S=diag([S(ω0),S(ω1),…,S(ωN-1)])是一个N阶对角矩阵，其对角元素等于发射信号s(t)的N点频域等间隔采样值；Eτ∈N×L是一个时延矩阵，矩阵中包含信号的全部多径时延信息；βk∈L×1包含第k簇的信道复数衰落的系数；wk=[W(k)(ω0),W(k)(ω1),…,W(k)(ωN-1)]T∈N×1是噪声的频域采样向量；Eτ的矩阵构成为

Eτ=[eτ1,…,eτj,…,eτL]。

(10)

式中：eτj=[1,e-jΔωτj,…,e-j(N-1)Δωτj]T。βk具体可表示为

(11)

现假设接收阵列距离信号源足够远，即接收阵列和信号源的距离远大于阵元的间距，因此认为信号以远场平行方式入射到接收阵列。图1所示为阵列结构拓扑，超宽带系统联合估计信号的TOA和DOA值一般仅需要两副接收天线。

图1 阵列结构拓扑

(12)

式中：d是阵列中两副天线的间距，c是光速。由上式就可以估计出DOA角度，即

(13)

式中：l=1,2,…,L。因此，要想估计信号源的DOA角度就需要先对两副天线的TOA进行估计。下面给出TOA估计的具体过程。

假设阵列接收系统中两副天线的频域接收信号分别为Y1∈N×K和Y2∈N×K，根据上述数据模型，Y1和Y2的具体表达式为

Y1=SEτB+W1，

(14)

Y2=SEζB+W2。

(15)

式中：S同式(9)；B=[β1,…,βk,…,βK]∈L×K表示信道复数衰落的系数；N×K和分别表示两副天线接收到的噪声；Eτ和Eζ分别表示两副天线的时延矩阵，

(16)

(17)

3 基于联合稀疏恢复的TOA和DOA估计方法

在快拍数为1的情况下，重新表示两副天线接收到的信号，分别为

y1=SEτβ+w1，

(18)

y2=SEζβ+w2。

(19)

式中：β=[β1,β2,…,βL]T∈L×1表示信道复数衰落系数，w1=[W1(ω0),W1(ω1),…,W1(ωN-1)]T∈N×1和w2=[W2(ω0),W2(ω1),…,W2(ωN-1)]T∈N×1分别是在单快拍数据下采集到的频域噪声向量。将时延矩阵Eτ和Eζ扩展为一个完备字典E，该字典E中包含所有可能的TOA信息并且满足即有

(20)

y1=SEh1+w1，

(21)

y2=SEh2+w2。

(22)

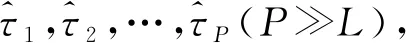
(23)

增强的稀疏表示形式为

y1=(E+E′Λ)ρ。

(24)

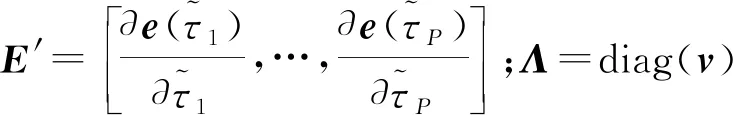
(25)

因此偏移向量v和ρ是联合稀疏。令σ=Λρ为一个稀疏向量，因此离网稀疏公式可以表示为

(26a)

s.t.h=[ρT,σT]T，

(26b)

(26c)

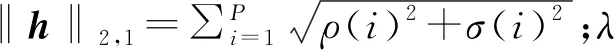
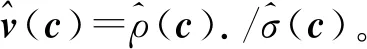
(27)

(28)

在对两副天线的时延都估计得到后，DOA估计值可由配对好的TOA之差得到，即

(29)

本文所提方法的主要步骤如下：

Step1 得到式(18)和式(19)中两副天线的单快拍数据向量y1和y2。

Step2 构造完备字典E，并将式(18)和式(19)分别转化成式(21)和式(22)的稀疏表示形式。

4 复杂度分析

以复乘次数作为复杂度评判标准，在相同的条件下分析采用传统CS算法和本文算法进行TOA和DOA联合估计的复杂度。对于本文方法，首先需要将发射信号和接收信号变换到频域模型S、Y1和Y2，复杂度为O(N2+2N2K)；根据公式(24)，对完备字典E求导，复杂度为O(PN)；OMP算法的迭代过程需要O{2LP(N-L)+2L(L+1)[L(L+1)/4+4(L+2)(N-L)/3]}，因此算法总的复杂度为O{N2+2N2K+PN+2LP(N-L)+2L(L+1)[L(L+1)/4+4(L+2)(N-L)/3]}。同理，传统CS算法的迭代过程需要O{LP′(N-L)+L(L+1)[L(L+1)/4+2(L+2)(N-L)/3]}，所以其总的计算复杂度为O{N2+2N2K+LP′(N-L)+L(L+1)[L(L+1)/4+2(L+2)(N-L)/3]}。

本文所提算法考虑了离网格情况，其网格数P≪P′，所以计算复杂度低于传统CS算法。

5 性能对比

定义信噪比

式中：y(t)表示天线的时域接收信号，w(t)表示接收信号时产生的加性高斯白噪声。定义均方根误差

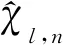
假设脉冲形成因子为Γ=0.25 ns，超宽带信号的平均发射功率为-30 dBm，脉冲信号的重复周期Tc=2 ns，每个符号的脉冲重复次数Nc=5，符号周期Ts=NcTc=10 ns。假设信号多径数目为L=3，每一个多径的复数衰落系数都是随机产生的并且已知，且多径幅度分别为β=[0.7,0.4e-jπ/2,0.2]T，3个多径信号到达两副天线的多径时延与波达方向角度分别为(τ1,ζ1,θ1)=(0.313 ns,0.242 ns,10°),(τ2,ζ2,θ2)=(0.462 ns,0.333 ns,20°)，(τ3,ζ3,θ3)=(0.628 ns,0.557 ns,30°)，信道内的噪声都是加性高斯白噪声。假设对天线接收信号进行N=64点频域采样，离网格字典中的网格间隔为0.01 ns。

图2和图3给出了在不同信噪比条件下本文所提算法与矩阵束方法、PM、ESPRIT算法、IST算法、LASSO算法以及传统压缩感知算法的TOA和DOA估计性能变化，可以看出，本文所提算法相较于其他算法具有更高的TOA和DOA估计性能。

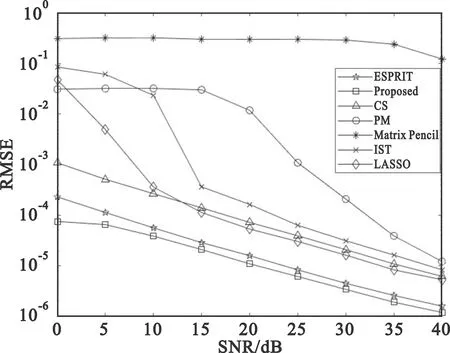
图2 不同算法TOA估计RMSE性能对比

图3 不同算法DOA估计RMSE性能对比

图4和图5给出了在不同信噪比条件下，当多径数变化时本文所提算法估计性能变化。从图4和图5可以看出，随着多径数的增大，本文所提算法的TOA和DOA估计性能均降低。原因在于当多径数增大时，信号之间的相互干扰就会增强，进而导致了算法的估计精度下降。

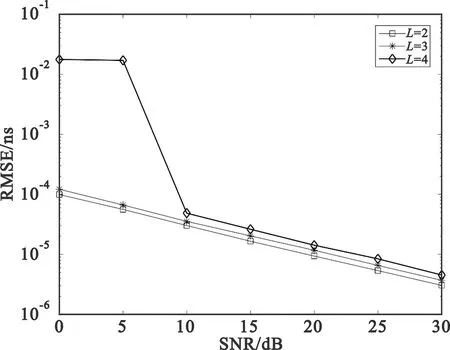
图4 本文所提方法在不同多径下的TOA估计RMSE性能对比

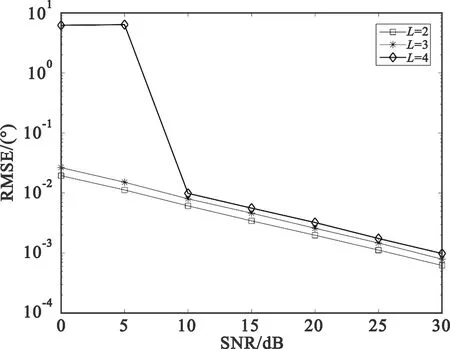
图5 本文所提方法在不同多径下的DOA估计RMSE性能对比

6 结束语

本文提出了超宽带系统中一种基于稀疏恢复的TOA和DOA联合估计方法。该方法首先将接收信号变换到频域，考虑信号TOA和DOA离网格情况建立参数化稀疏模型，在稀疏表示框架下，经过联合稀疏恢复后，利用JOMP算法对信号到达两副天线的TOA进行估计，最后根据TOA与DOA的关系计算信号的DOA估计。所提算法解决了二维参数的配对以及离网格信号参数估计问题，具有较高的参数估计性能。仿真结果表明，所提算法在单快拍条件下可以获得较好的参数估计性能，且估计性能优于传统的PM算法、矩阵束方法、IST算法、LASSO算法和传统基于稀疏表示的方法。

下一步将考虑非同步信号接收的情况，针对异步效应消除的问题展开研究。