一种民用无人机反制系统评估方法*
程 擎,伍瀚宇,吉 鹏,焦浩博,张 强
(中国民用航空飞行学院 空中交通管理学院,四川 广汉618307)
0 引 言
近年来,随着无人机领域的迅猛发展,使用门槛不断降低,在尚未完善的无人机监管体系下,大量黑飞、操作不当引发的安全事故频频发生。此外,“低慢小”无人机所占据的低空空域是宝贵的战略资源。为保障低空空域的安全可靠,保障公众的人身安全与隐私权,无人机反制技术应运而生。
无人机反制技术主要通过人眼捕捉或监视设备锁定目标后,利用捕捉网、激光、声波、火力压制、无线电干扰等手段,对目标无人机进行捕捉、摧毁、控制等。当前,无人机反制技术在防范恐怖袭击,保护重要地点、重大活动现场,维护社会治安秩序方面发挥着重要作用[1-2]。
无人机反制技术手段众多,不同处置方式的作用效果不同,且不同规格参数的反制设备性能也具有一定的差异。为了对各反制设备的性能进行评估,国防科技创新特区主办了“无形截击”无人机与反无人机对抗挑战赛,采用模拟城市中反制无人机的情形,随机方位“入侵”多架无人机,以成功处置得分、造成负面影响扣分的方式,对无人机反制系统进行评估。该评价体系具有现实意义,评估手段直接有效,但是在评估过程中会受到操作人员、环境、随机性等因素的影响。因此,本文在控制环境变量的条件下,利用无人机反制系统进行多次重复处置试验,采集相关的指标数据,建立并完善评价体系,以完成对无人机反制系统的评估。
1 无人机反制系统评估指标
无人机反制系统的评估即为对该系统从开始处置目标无人机到处置结束的整个过程以及设备自身性能的评估,不仅仅包括对处置效果的评估,还需考虑到在整个处置过程中所具有的二次灾害风险、设备对于操作人员的易用性以及设备质量。因此将处置效果、二次灾害、易用性、设备质量作为无人机反制系统评估中的一级指标,建立评估指标体系,如图1所示。

图1 无人机反制系统评估指标体
一级指标处置效果可以细化为处置成功率、处置时间、处置结果、处置距离4个二级指标。
(1)成功率:处置成功率直接体现了无人机反制系统处置无人机的有效性,通过在试验中对每种反制系统进行10次处置试验,根据目标无人机逃脱次数描述该系统的处置成功率。
(2)处置时间:若一次处置过程中消耗时间过长将会严重影响目标的处置效果,甚至错过最佳处置时机,可用每次处置活动开始时间与结束时间差值度量处置时间。
(3)处置结果:不同反制系统在处置无人机时,根据其原理不同往往有不同的作用效果,既可能出现击毁坠落、干扰逼降,也可能出现悬停与飘离后果,因此可用处置导致结果与期望结果对比,得到对处置结果指标的评估。
(4)处置距离:有效处置距离的评估指标值主要根据在实际反制场景中,设备能够达到的较为可靠的理想处置距离进行度量。
一级指标二次灾害可细化为火势、冲击力、坠落范围、电磁污染4个二级指标。
(1)火势:无人机反制系统中有部分反制武器会令目标燃烧,落地后火焰对周边环境形成了安全隐患,为反映火势情况,可由受到处置后产生的火焰面积与无人机面积之间的比值进行衡量。
(2)冲击力:冲击指标主要是衡量目标坠落时对地面威胁程度,可转换为对目标近地时的速度大小的评估。
(3)坠落范围:坠落范围也是衡量目标坠落时对地面威胁程度,可以转换为对目标落地位置与受到处置时的位置距离大小的评估。
(4)电磁污染:电磁污染指标则利用频谱检测仪对处置过程中,周边环境中重要无线电频段的抬升情况进行考虑。
一次指标中的易用性指标分别根据对反制人员操作学习与实际使用过程中的难度、处置过程中设备处置波束宽度以及便携程度三个方面对其进行评估。
设备质量指标主要为对可信性和可用性两个二级指标评估,其中可信性的评估为综合考虑设备的平均修复时间、故障率,可用性的评估为综合考虑设备的修复率、维修度、可靠度、平均寿命。
该无人机评估模型的建立与指标设定主要以民航机场或电磁环境敏感区域作为处置背景,在对一些其他环境进行评估时模型可能会失效,需要对一级或二级指标进行适当调整;并且处置试验环境应处于非极端气候环境,否则如坠落范围、冲击力、处置结果等多个二级指标都会受到环境因素的影响,得到错误的评估结果。
2 无人机反制系统评价体系
在对反制系统的评估体系中,评估语义集如下所示:
V={υ1,υ2,υ3,υ4,υ5} 。
(1)
式中:评价结果依次递增,即υ1为差,υ2为较差,υ3为中等,υ4为较好,υ5为好。在评价体系中指标的评估过程中,得到的具体数值无法直接与评估语义进行关联。为此,引入模糊综合评价模型,采用隶属度概念对指标数据中的模糊界限进行解释[3-4]。通过德尔菲(Delphi)法建立各个指标的隶属函数,征询目标包括无人机反制领域专家、一线工作人员、无人机飞手、应用机构专家、无人机反制企业专家。结合专家组意见,建立隶属函数,统一不同指标数据纲量,反映各指标元素与评估语义集的所属关系。
隶属函数为指标数据值与隶属评价结果的概率的对应关系,常见的函数图形包括三角形与梯形模糊隶属函数图形。令评估语义集V中不同结果对应的隶属函数表示为
U={μ1,μ2,μ3,μ4,μ5},
(2)
其隶属函数表达式如下:
(3)
(4)
(5)
式中:μ3(x)、μ4(x)表达式与μ2(x)相似。
根据指标数值在隶属函数中所对应的模糊分布向量rμn(n=1,2,3,4,5)可以得到某一评估指标的评估隶属向量
γ1=(γμ1,γμ2,γμ3,γμ4,γμ5)。
(6)
将无人机反制系统中各评估指标的评估隶属向量集合可以得到模糊评价矩阵
R=(γ1,γ2,…,γn)T。
(7)
此时得到的模糊评价矩阵中各指标所占权重相等,但在实际评估时,不同一级指标之间以及同一一级指标下的二级指标之间的重要程度是不同的,因此需引入不同各指标的权重值。综合考虑后采用模糊层次分析法确定指标权重,这种方法不仅比普通层次分析法的一致性检验更加容易,而且一致性的判断标准更加科学、准确、简便[6-8]。
首先针对上一层中某元素,对该层中的各元素之间的相对重要性进行比较。以元素处置效果U1为例,其下一层次中元素为处置成功率、处置时间、处置结果、处置距离,即U11、U12、U13、U14,构造模糊互补矩阵FU1=(fij)4×4,如图1所示。在两个元素之间进行比较时,为对相对重要程度进行描述,采用0.1~0.9进行标度。在此标度过程中,0.5表示元素U1i和元素U1j同等重要,当标度越接近0.9时表示元素U1i比元素U1j越重要,而标度越接近0.1时则表示元素U1i比元素U1j越不重要[9-10]。

图1 评估指标模糊互补矩阵
将模糊互补矩阵转换为模糊一致矩阵,得到新的矩阵QU1=(qij)4×4,其中qij为
(8)

(9)
对得到的模糊评估矩阵中各指标乘上其权重值,可以得到最终的综合模糊评估结果向量为
B=W×R=(b1,b2,…,bn) 。
(10)
为了能够令评估得到的各个无人机反制系统之间能够有显著的比较方式,因此采用平均加权法将最后的结果换算为百分制得分。令S={s1,s2,s3,s4,s5}={0,25,50,75,100},带入可得评估分值为
(11)
3 无人机处置试验与结果分析
3.1 无人机处置试验
无人机处置试验于郊外某试验场地进行,天气晴朗且地面静风。在无人机反制系统的选择中,激光武器、无线电干扰设备在反制“低慢小”无人机时具有较好的有效性、连续性,并且分别为当前无人机反制“硬杀伤”与“软杀伤”中的具有代表性的典型反制系统,无论是处置效果还是二次灾害的表现方面,在一定程度上都代表了这一类反制系统的无人机处置能力。在试验中选用的反制系统设备均已参与了大量无人机处置演练,具有优异的实战成绩,并且无线电干扰设备已广泛用于城市无人机反制应用,因此可以认为所选用的试验设备具有较好的代表性。
无人机处置试验选用激光打击、控制信号干扰、定位信号干扰三种反制手段进行评估,根据拟定的无人机反制系统评价体系制定各评估指标的采集方案,在控制处置环境变量不变的条件下进行试验并采集所需数据[11]。其中针对多组不可定量指标采用评估语义集V={υ1,υ2,υ3,υ4,υ5}进行表示。
3.1.1 激光打击试验
激光打击主要利用激光的高能量,对目标无人机聚焦瞄准灼烧,破坏重要部件,导致目标无人机失去控制并坠毁。打击过程中可持续攻击,作用距离远且无需考虑弹道与天气影响,具有效费比高、发射成本低、良好摧坚能力的优点,可以击穿各类金属与非金属材料。
激光打击试验中,目标无人机由图2中无人机图标位置起飞至80 m高度悬停,激光设备置于图中标记位置距无人机水平距离650 m。目标无人机于起飞点垂直升空至80 m高度,激光设备光电子系统捕捉并跟踪无人机,3 s倒计时后发射激光波束,当目标无人机出现坠落倾向后停止出光。

图2 激光打击试验场景俯视图
3.1.2 控制信号干扰试验
空间中的电磁环境复杂且不稳定,存在有不可避免的多路径效应。而无人机为避免数据链受到干扰,具有一定的射频干扰自适应抑制能力,但一旦无线电干扰超过阈值,就能阻断无人机与操作员之间的数据链路[12-13]。
当前无人机数据链路多为2.4 GHz、5.8 GHz频段的慢跳频系统。控制信号干扰试验中,借助增益天线,向目标发射2.4 GHz、5.8 GHz频段的无线电信号,实现阻塞干扰。试验中以220 m、120 m、50 m对2 400~2 486 MHz、5 720~5 850 MHz频段分别进行了3次、2次、5次处置的拉锯试验。飞手距离无人机水平距离50 m,无人机于指定位置50 m高度空中悬停,其位置分布如图3所示。
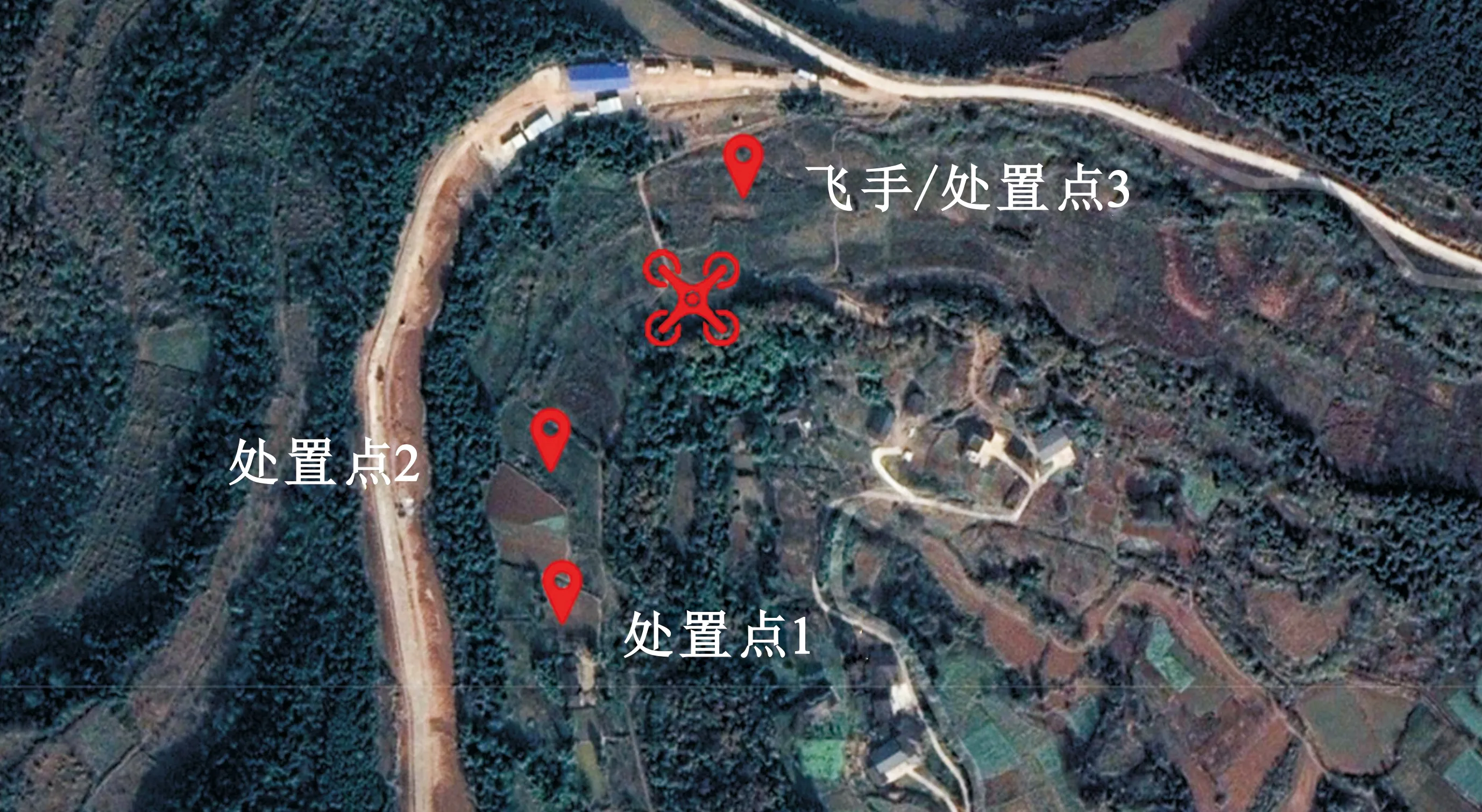
图3 无线电干扰试验场景俯视图
由于在实际干扰过程中,无人机在受到影响的同时也在采取一定的手段,如扩频、跳频,以抗衡环境中的干扰,维持与飞手之间的上下行数据链通信,所以在无线电干扰的试验中,反制点与无人机之间的距离并不能直接表现出反制设备的有效作用距离。当控制端越靠近无人机时,受到信号干扰的表现越弱;反之越远离无人机时,受到信号干扰的表现越强烈。因此,试验中保持了飞手与无人机50 m的距离不变,以多组距离试验采集无人机受到信号干扰的数据。
3.1.3 定位信号干扰试验
由于全球卫星导航系统采用直接序列扩频通信,具有载波频率公开固定、发射功率小、抗干扰的特点,试验过程中只需要对准频率发射大功率无线电信号便能实现阻塞干扰。
定位信号干扰试验中,与控制信号干扰位置布局相同,无人机靶机起飞与悬停位置以及无人机与飞手50 m间距不变,反制组于距目标无人机220 m的处置点1处,对其1 560~1620 MHz频段实施10次干扰处置试验。
在无线电控制信号与定位信号干扰试验中,无线电干扰枪无瞄准倍镜,所有处置过程均由目视捕捉,跟踪打击。试验时,由无人机升空飞往指定坐标,升至50 m高度,反制组瞄准无人机所处大致方位进行不间断无线电干扰。干扰期间,飞手通过图像反馈与不断进行规律性运动判断无人机控制链路和图传链路是否正常。当持续1 min无线电干扰仍无效果或无人机受到干扰并呈现出明显返航降落或无人机失控飞离视场后,停止处置,飞手飞回无人机。
3.2 处置试验结果分析
3.2.1 激光打击试验结果
在激光打击试验中,无人机处置效果较好,大部分处置试验均在极短时间内达到了目的,受到处置的无人机多为击中机身电池,失去动力,直接坠落。在最后两次处置试验中,由于未能及时击穿机身摧毁电池,持续出光多次才最终击落无人机。
激光打击无人机时,无论击中机翼还是电源都会产生火焰,特别是在击中电源时,还会引发锂电池燃烧。在所有试验中都具有火灾安全隐患,不过在停止激光打击或无人机高速坠落时,火势具有明显减弱趋势。其中第三次试验时,由于只击中了无人机机翼,并未破坏其动力系统,导致无人机失控飘移。由激光武器反馈光电图像数据可知,在出光过程中,其原理为光电追踪目标,引导出光点位置,因此目标被击落快速下降时,可能会诱导误伤到其他物体或树木等。激光打击试验结果如表1所示。
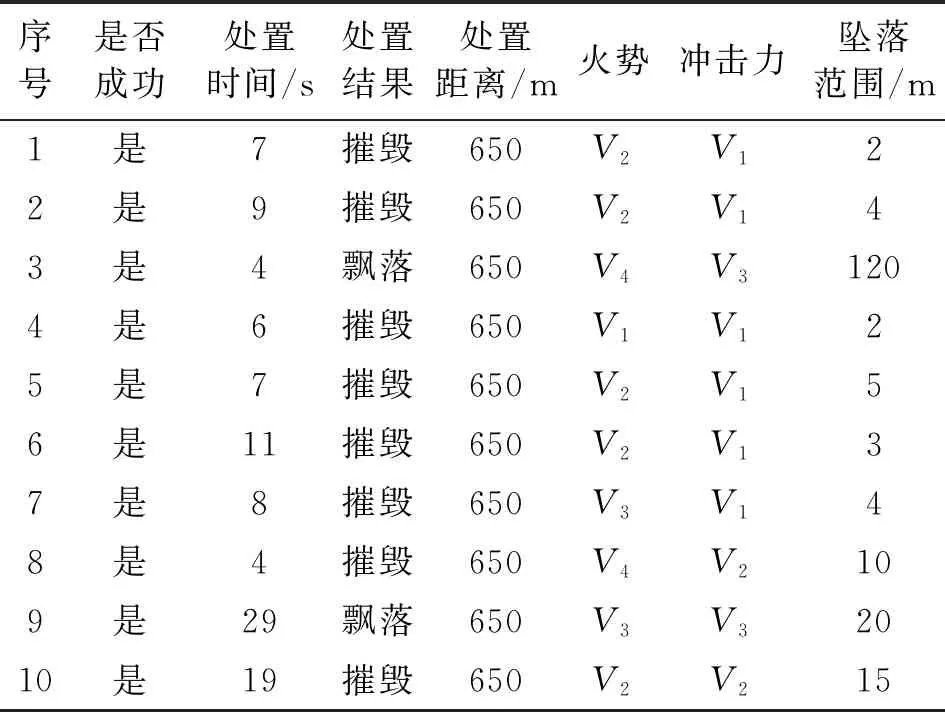
表1 激光打击试验
激光打击试验时,周边电磁环境变化如图4所示,在监测频段内底噪没有明显抬升,激光打击试验前后均方差为1.180 5 dBμV,属于正常波动范围,可见激光武器采用的光学能量对周边电磁环境不会造成污染。

图4 激光打击试验前后电磁环境对比
3.2.2 控制信号干扰试验结果
控制信号干扰试验中,目标无人机与飞手之间距离保持50 m不变,反制组从距目标220 m处实施2.4 GHz、5.8 GHz频段干扰,共进行3次试验,处置时间均为1 min以上。处置期间无人机不断执行规律运动,控制链路没有受到任何干扰,图传链路信号间歇性丢失。反制组从距目标120 m处实施无线电干扰,共进行2次试验:第一次试验处置时间1 min以上,控制链路无干扰,图传链路丢失;第二次试验处置时间15 s,目标失控飘落。反制组从距目标50 m处实施无线电干扰,共进行5次试验,处置时间均为30 s以内,其中两次悬停,三次触发返航。试验结果如表2所示。
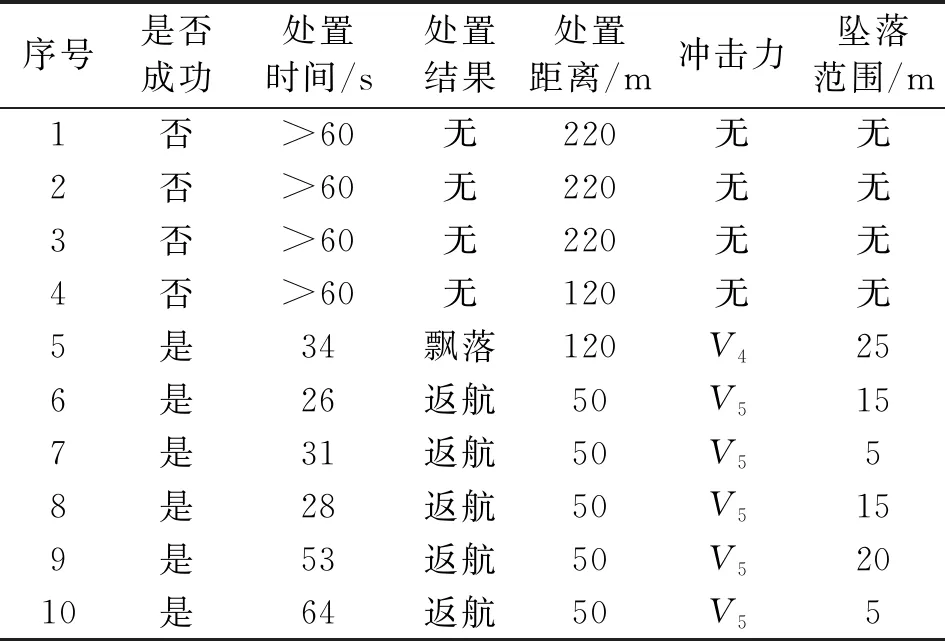
表2 控制信号干扰试验结果
考虑到无线电干扰可能的危害性,特别是在民航领域,恶劣的电磁环境直接威胁航空运输的安全[14]。以民航导航设备为例,可能受到影响的包括测距仪台(962~1 212 MHz)、二次雷达(1 030 MHz、1 090 MHz)、导航卫星(1.5 GHz)、ADS-B(978 MHz、1 090 MHz),因此无线电频谱检测仪主要采集1~1.6 GHz的频谱变化,其中,图5为在1~1.6 GHz频段周边环境电磁辐射情况与控制信号干扰时的频谱图,图6为环境底噪与干扰试验时的频谱差值图。
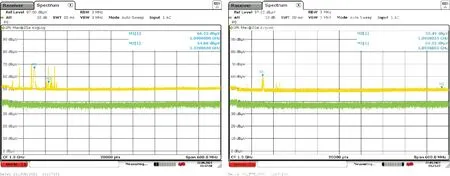
图5 电磁环境与控制信号干扰时频谱对比图

图6 环境底噪与干扰试验时的频谱差值图
从图5和图6可见,干扰试验时,该频段底噪没有明显抬升情况。经过计算,干扰试验前底噪均值为37.179 4 dBμV,前后均方差为1.178 8 dBμV,属于正常波动情况。这些数据可以说明在与民航相关的重要频段范围内,电磁干扰基本无影响。
3.2.3 定位信号干扰试验结果
目标与飞手距离50 m,反制组从距目标220 m处进行1.5 GHz频段的无线电干扰,共进行10次试验,其中仅有一次失败。试验结果如表3所示。
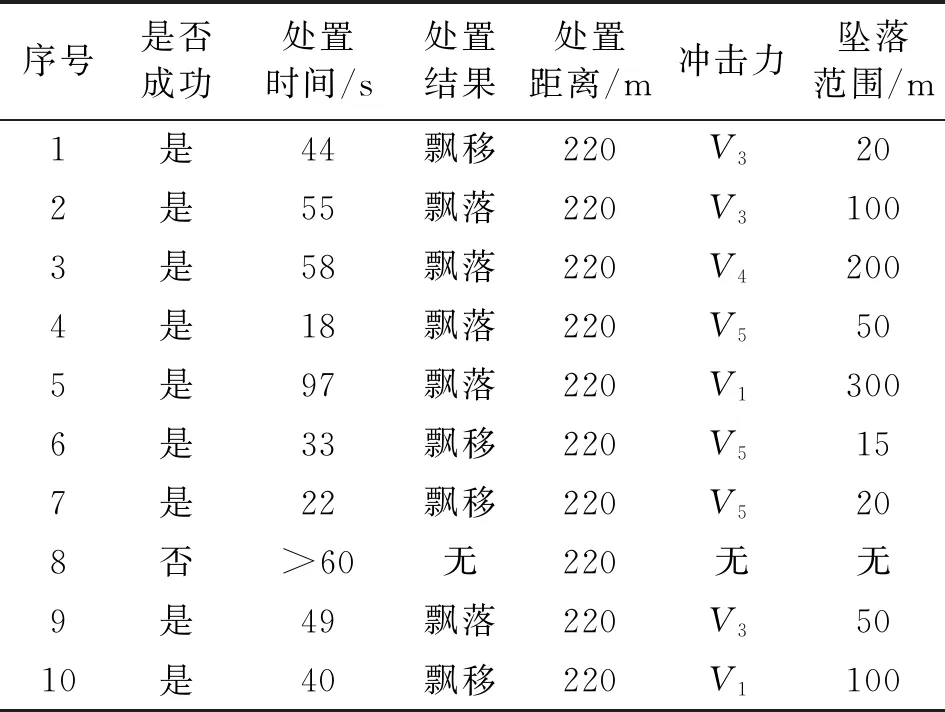
表3 第一组定位信号干扰试验
与控制信号干扰试验中一致,使用无线电频谱检测仪采集1~1.6 GHz的频谱变化,图7和图8分别为在1~1.6 GHz频段周边环境电磁辐射情况与定位信号干扰时的频谱图以及均值检波的差值图。

图7 电磁环境与定位信号干扰时频谱对比图
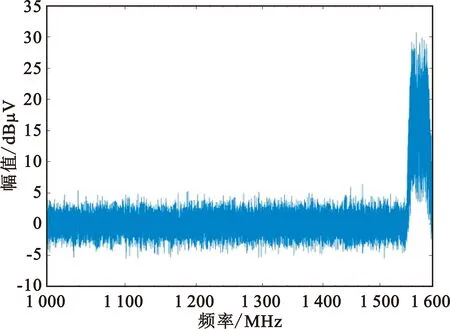
图8 环境底噪与干扰试验时的频谱差值图
由图7和图8可见,在使用反制设备干扰无人机定位信号时,1.58 GHz左右各30 MHz区间范围内,平均值检波与峰值检波都出现了较大幅度的抬升,峰值达到了95 dBμV。经过计算可得,试验前环境底噪均值为37.086 1 dBμV,在1~1.55 GHz频段内均方差为1.193 3 dBμV,处于正常波动,对电磁环境基本无影响;但是在1.55~1.6 GHz频段内发生剧烈抬升,均方差达到了9.346 4 dBμV,已超出可接受范围,对电磁环境造成了极大干扰,对周边设备的无线电信号特别是导航卫星信号造成了严重影响。
4 无人机反制系统评估与结果分析
根据无人机反制技术专家组意见,建立下层二级评估指标比较矩阵,针对同一一级指标分支下的各二级指标的重要性进行比较,以一级指标处置效果的下层评估指标为例,得到比较矩阵如图9所示。

(a)处置效果
在评估指标设备质量中,针对可信性与可用性进行比较评估得到的模糊矩阵中评估比较值为0.7、0.3。根据公式(8)、(9)可以求得各二级指标的权重向量,无人机处置效果各二级指标权重为WU1=(0.3,0.237 5,0.256 3,0.206 3),二次灾害二级指标各权重为WU2=(0.2,0.225,0.287 5,0.287 5),易用性二级指标权重分布为WU3=(0.288 9,0.366 7,0.344 4),设备质量二级指标权重分布为WU1=(0.55,0.45)。
根据对无人机反制系统评估中一级指标进行评估,可得到比较矩阵如图10所示。

图10 无人机反制系统评估一级指标比较矩阵
同理得到关于无人机反制系统评估的一级指标权重分布为WU=(0.312 5,0.275,0.212 5,0.2)。
根据德尔菲法反馈的专家意见中,将无争议的值域的隶属度以1表示,将有争议部分模糊处理,以评估指标处置效果中各二级指标的隶属度分布为例,得到隶属函数图如图11所示。

图11 指标隶属函数图
针对C13中各评估标准为确定值,无需模糊处理,直接根据评估语义集V进行赋值,得到处置结果为(击毁坠落、逼降,飘落,悬停、返航,空中飘移,无反应)=(υ5,υ4,υ3,υ2,υ1)。
同理建立关于一级评估指标二次灾害、易用性、设备质量的下层指标的模糊分析,得到相应的模糊隶属函数。将试验中所得的结果代入至模糊隶属函数中,可以得到各指标的隶属向量。将各二级指标评估隶属向量集合得到的模糊评价矩阵与对应的权重集进行运算,得到上层一级指标的隶属向量Ri=WUi×ri。最后将一级指标隶属向量构成新的矩阵R=(R1,R2,R3,R4),与一级指标权重向量WU做运算处理,得到评估结果向量B=(b1,b2,b3,b4,b5),三组无人机反制手段分别累积10次处置试验数据后,其评估结果为

根据平均加权法转化为百分制得分,最终的评估得分如图12和表4所示。

图12 反制评估得分对比图

表4 无人机反制系统评估结果
5 结束语
在“低慢小”无人机反制技术领域的不断发展过程中,亟需对不同反制技术手段的评估对比,为不同应用场景中的选择提供依据,同时促进反制技术的发展。本文针对无人机反制技术的原理与特点,拟定了无人机反制系统评价体系,提出了一级评价指标以及相应的二级指标,并且根据专家组意见建立了各指标的隶属度函数图像。为获取无人机反制数据,进行了利用激光打击、无线电干扰的无人机处置试验,采集了评价体系中各二级评估指标的试验数据。基于试验所得数据,从处置效果、二次灾害、易用性、设备质量四个角度进行评估,通过计算得到了不同反制系统的评价得分,实现了不同反制技术手段之间的评估对比,其结论与实际试验中专家组评估结果相同,证明该评价体系具有可行性。
在对不同反制系统的评估对比过程中,还存在有许多误差因素:首先,由于条件限制,处置试验的数组过少,试验数据量缺乏,导致试验评估结果受到某一组试验数据突变的影响较大;其次,在进行试验的过程中,难以保证每一组试验的试验环境完全相同,风向风速、无人机悬停高度与位置都会有一定的误差,并且其误差对指标的评估也会产生一定的影响。因此,为弱化误差对评估结果的影响,后续还需采集更大的处置数据库对评估模型进行支撑。

