一种基于OFDM-LFM信号的PD雷达解模糊方法*

严济鸿，董海洋，翟鉴枢，杨 礼

(1.电子科技大学长三角研究院(衢州),浙江 衢州324000； 2.电子科技大学 信息与通信工程学院，成都 611731)

0 引 言

数字化的阵列雷达收发均以数字方式实现，较传统相控阵雷达有着精度高、动态范围大、波束形成灵活度高、可靠性强、低损耗等众多优势[1]，目前已发展为雷达领域的主流。

数字阵列雷达因其具备软件化的特点，在改变发射波形、接收信号处理和切换收发体制等方面有着诸多便利。脉冲多普勒(Pulse Doppler,PD)体制便是数字阵列雷达在搜索阶段常采用的体制，且通常采用收发共用天线且收发相互切换的方式。采用接收和发射状态相互切换的好处在于，不会因为发射泄露而影响雷达对目标回波的接收。

对于脉冲体制的雷达，当目标运动引起的多普勒频率大于发射脉冲的重复频率的一半时，就会产生速度模糊；当目标回波的延迟时间大于发射脉冲的重复周期时，会产生距离模糊。为解决速度模糊问题，可以采用高脉冲重复频率(High Pulse Repetition Frequency,HPRF)工作方式，但同时也带来了距离模糊问题[2]。为解决距离模糊问题，传统的方法是采用几种不同的脉冲重复间隔(Pulse Repetition Interval,PRI)，PRI的选择通常是根据余数定理、一维集算法、查找表法等，但以上方法需要雷达频繁的切换状态，这无疑会大大增加雷达系统的复杂性。

线性调频(Linear Frequency Modulation,LFM)信号是广泛使用的脉冲压缩信号。文献[3]采用正交频分的线性调频信号(Orthogonal Frequency Division Multiplexing Linear Frequency Modulation,OFDM-LFM)，很好地解决了合成孔径雷达(Synthetic Aperture Radar,SAR)成像的距离模糊问题。为解决PD雷达的速度和距离模糊问题，本文采用高脉冲重复频率的方式，在雷达最大作用距离所对应的时间内发射多个OFDM-LFM脉冲信号，这些信号具有较低的互相关峰值，可以有效地解决距离模糊问题。在接收端对多组发射脉冲信号所对应的回波进行数据重排，然后进行脉冲压缩、动目标检测(Moving Target Detection,MTD)处理，最终得到的峰值可以无模糊地体现目标的距离和速度。

1 信号模型及问题描述

对于脉冲体制的雷达，距离模糊是由于目标的回波延时大于脉冲重复间隔，如图1所示，此时目标回波不会落在本周期内，所测得的目标距离不是真实距离，由此产生模糊[4]。图1中，sm(t)表示第m个发射脉冲，rm(t)表示第m个发射脉冲的回波，τ0是目标回波的延时，则发射信号可以表示为

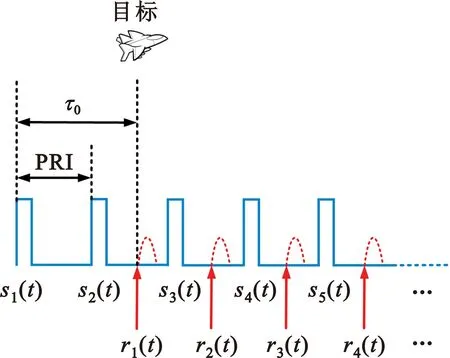
图1 产生距离模糊的回波示意图

(1)

式中：s(t)为脉冲压缩信号(常见的脉冲压缩信号主要有线性调频信号和相位编码信号)，tPRI为一个PRI所对应的时间。

脉冲雷达对目标距离的计算是通过测量目标回波r1(t)的延时τ0，而τ0需要通过脉冲压缩后的峰值位置进行估计。脉冲压缩一般采用匹配滤波器实现，而匹配滤波器就是在做互相关运算。当目标的回波延时τ0大于PRI时，r1(t)与s2(t)做互相关运算，如式(2)所示：

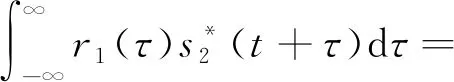
(2)

此时峰值位置为t=τ0-tPRI，该峰值所反映的延时与目标真实的回波延时τ0不相同，由此出现距离模糊。而如果通过时分的方式发射一组互相关峰值较低的脉冲信号，r1(t)只有和s1(t)进行互相关运算时才会出现峰值，和s2(t)进行互相关运算时就不会出现峰值，便可以有效解决距离模糊问题。r1(t)与s1(t)做互相关运算，如式(3)所示：

(3)

此时峰值位置为t=τ0，通过该峰值位置就可以正确地计算出目标的距离。

2 发射信号设计

由第1节可知，以时分的方式发射一组互相关峰值较低的信号可以解决距离模糊问题，本文采用OFDM-LFM信号来设计发射信号集。首先LFM信号的表达式为

(4)

式中：u(t)为长度为Tp的矩形窗函数；f0为线性调频信号的中心频率；μ=B/Tp为调频斜率，B为线性调频信号的带宽。M个OFDM-LFM信号可以按照式(5)产生：

(5)

式中：fp=1/Tp。可以证明si(t)和sj(t)相互正交，即

(6)

并且可以证明在式(6)中，两个信号sm(t)和sn(t)的间隔|m-n|越大，两个信号的互相关峰值越低[5]。

3 雷达信号处理流程

3.1 发射端处理流程

本文采用高重频的方式发射脉冲来解决速度模糊，并且以时分的方式发射具有低互相关峰值的脉冲信号来解决距离模糊，这些脉冲信号由第2节设计的OFDM-LFM信号集组成，它们具有较低的互相关峰值，可以有效地解决距离模糊。发射参数的具体设计流程如下：

首先根据雷达距离分辨率δr确定单个线性调频信号的带宽B，即

(7)

式中：c为光速。然后根据雷达距离盲区Rb确定脉冲宽度τ，即

(8)

传统PD雷达的PRI(PRF的倒数)需要根据最大无模糊距离Rmax和最大无模糊速度vmax同时确定，而本文方法的PRI只根据最大无模糊速度vmax确定，即

(9)

式中：fdmax是由最大径向速度vmax引起的最大多普勒频率。接下来根据雷达最大无模糊距离Rmax确定雷达周期Tmax，即

(10)

同时确定在一个雷达周期Tmax内发射脉冲的个数m，即

(11)

式中：「·⎤表示向上取整。然后利用第2节中所述的OFDM-LFM信号设计方法产生一组发射信号集，并在雷达最大探测距离所对应的时间Tmax内发射m个信号(如图2所示，在一个Tmax内发射a1,a2,…,am共m个信号)，这些信号具有较低的互相关峰值。为了得到对目标回波较好的检测效果，雷达系统通常需要做积累。本文发射多个雷达周期Tmax构成一个相参处理周期(Coherent Processing Interval，CPI)，以方便接收端做相参积累。具体一个CPI内包含多少个Tmax，可以根据实际场景进行选择。

图2 发射信号示意图

3.2 接收端处理流程

3.2.1 将回波数据重排成矩阵

对于收发切换体制的雷达，在发射时间内接收机无法采集数据，因此接收机在第1个Tmax内采集的回波数据序列R1为

(12)

式中：0an(n=1,2,…,m)表示在发射信号an(n=1,2,…,m)时的接收数据，如图2所示，此时雷达处于发射状态，因此接收数据为0；ran表示在发射信号an后转换为接收模式时的接收数据。上述接收数据都是针对已经下变频到基带的数字信号。

在雷达的一个相参处理周期CPI内包含多个Tmax，将一个CPI的回波数据排成回波数据矩阵R:

(13)

矩阵R的排列方法如图3所示。该数据重排方式和传统PD雷达的数据重排方式不同，传统PD雷达的每一行的长度为一个PRI，而该方法得到的矩阵的每一行的长度为Tmax。矩阵R的第1行起始时刻为a1信号开始发射的时刻，时间长度为Tmax，第2行起始时刻为a2信号开始发射的时刻，时间长度也为Tmax，后续的行以此类推。

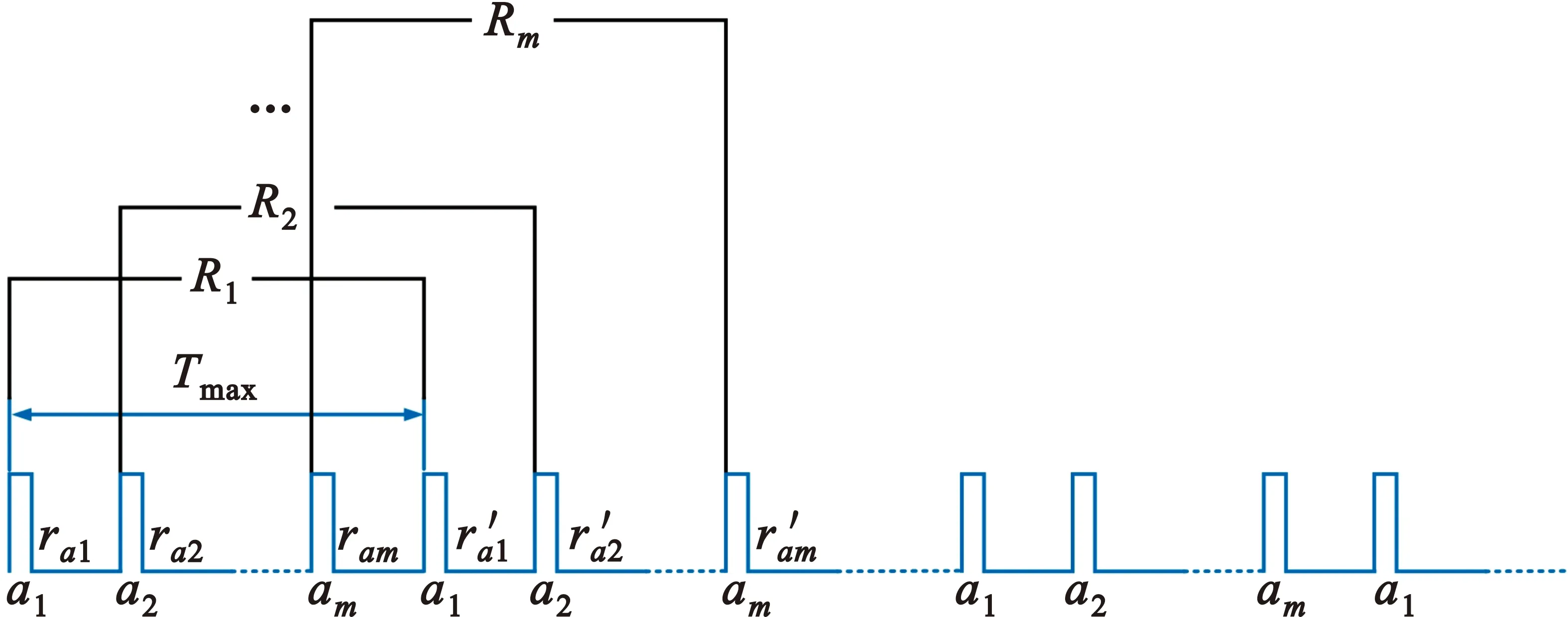
图3 数据重排示意图

传统方法数据矩阵快时间维的长度为PRI，慢时间维的采样频率是PRF(PRI的倒数)，而本文方法数据矩阵快时间维的长度为Tmax(m倍PRI)，慢时间维的采样频率仍然是一个PRF。由于数据矩阵快时间维的长度正比于最大无模糊距离，慢时间维的采样频率正比于最大无模糊速度，因此在相同的最大无模糊速度的前提下，本文方法的最大无模糊距离为传统方法的m倍，m的取值见式(11)。

3.2.2 脉冲压缩

得到回波数据矩阵R后，对矩阵R的每一行进行脉冲压缩处理。矩阵R第1行的回波R1与A1做匹配滤波，A1是在发射信号a1后面补0，使得A1与R1是等长的时间序列。采用频域脉冲压缩的处理方法，处理方法如下式：

X1=IFFT{FFT{R1[n]}·FFT{(A1[-n])*}}。

(14)

式中：FFT(Fast Fourier Transform)为快速傅里叶变换，IFFT(Inverse FFT)为逆快速傅里叶变换，A1[-n]表示将序列A1反转，()*表示共轭运算。

矩阵R第2行的回波R2与A2做匹配滤波，A2是在发射信号a2后面补0，使得A2与R2是等长的时间序列，同样采用式(14)的频域脉冲压缩的处理方法。对矩阵R的其余行做同样的处理，处理完的数据放入新矩阵X的相应行中。

3.2.3 MTD

对经过脉冲压缩处理后得到的新矩阵X的每一列进行FFT，即做动目标检测处理，实现相参积累，得到的新矩阵内的峰值即可体现出目标的距离和速度信息。

4 仿真与分析

假设某探测场景下要求雷达的距离分辨率δr≤50 m，距离盲区Rb≤1 000 m，最大可探测距离为Rmax=100 km，最大可探测速度为vmax=260 m/s，则根据雷达信号处理流程中发射参数的计算公式，为了满足距离分辨率δr的需求，每个线性调频信号的带宽至少为

(15)

为了满足距离盲区Rb的需求，发射脉冲宽度最多为

(16)

如果选择雷达的射频频率fRF=3 GHz，则波长为λ=c/f=0.1 m，那么脉冲重复间隔需满足

(17)

根据最大探测距离为Rmax的需求，雷达周期Tmax至少为

(18)

考虑到以上需求，设置雷达的发射参数如下：

(19)

由此可以得出距离分辨率为

(20)

距离盲区为

(21)

若采用本文的方法，最大无模糊距离和最大无模糊速度分别为

(22)

(23)

若采用传统PD雷达的方法，最大无模糊距离和最大无模糊速度分别为

(24)

(25)

显然，传统PD雷达无法满足这种场景下的Rmax需求，而要想满足Rmax的需求，就必须增大脉冲重复间隔为

(26)

从而最大无模糊距离和最大无模糊速度变为

(27)

(28)

此时又无法满足vmax的需求，因此传统PD雷达无法同时满足这种场景下Rmax和vmax的需求，而本文提出的方法可以应对这一场景。下面就给出传统雷达和本文方法的仿真结果，通过对比来验证本文方法的可行性与优越性。

首先设置单个线性调频信号的带宽为3 MHz，两个线性调频的中心频率间隔为fp=6 MHz，设置采样率为100 MHz，根据式(19)，共设计8个OFDM-LFM信号，每个信号的自相关函数如图4所示，信号间的互相关函数如图5所示，可以看到信号间具有较低的互相关峰值。

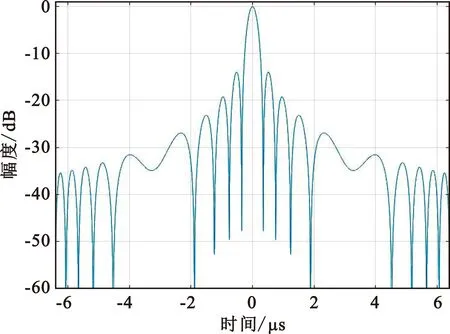
图4 自相关函数图

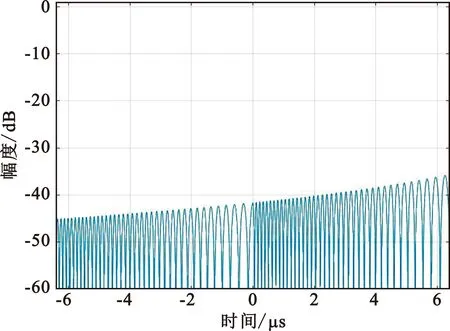
图5 互相关函数图

为了验证本文方案的可行性，共对目标的两种可能的场景进行了仿真实验，如表1所示，其中，场景1是最常见的发生距离模糊的情况，场景2则是另一种较极端的发生距离模糊的情况，即两个目标的延时刚好相差整数倍PRI。

表1 仿真实验中目标两种可能的场景

4.1 单目标

假设只有一个目标，距离为24 km，速度为60 m/s，此时的回波示意图如图6所示，目标的回波延时t1>PRI，即目标距离超出了传统雷达的最大无模糊距离，但是在本文方法的最大无模糊距离范围内。

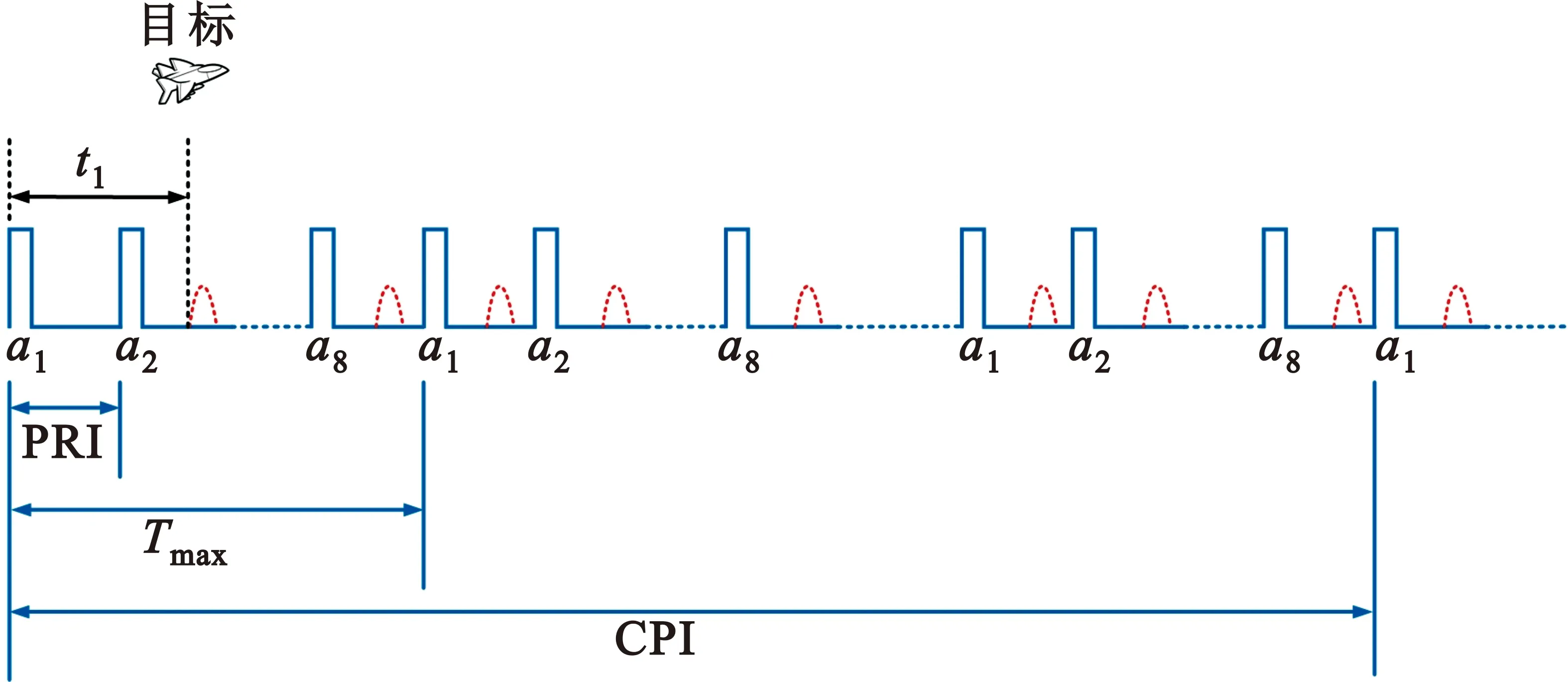
图6 单目标回波延时大于PRI时的示意图

仿真设置信噪比为-15 dB，采用式(19)所示的发射参数，传统PD雷达的最大无模糊距离和最大无模糊速度为式(24)～(25)，传统PD雷达只采用一种线性调频发射波形，其动目标检测图如图7(a)所示，可以看到计算的距离和设置的距离不一致，并且计算的距离刚好等于真实距离减去最大无模糊距离，传统雷达难以分辨目标是否在最大无模糊距离范围内，因此产生了距离模糊。而采用本文方法，最大无模糊距离和最大无模糊速度为式(22)～(23)，采用OFDM-LFM信号作为发射信号，这些信号具有较低的互相关峰值，其MTD图如图7(b)所示，计算的距离和设置的距离是一致的，不会产生距离模糊。

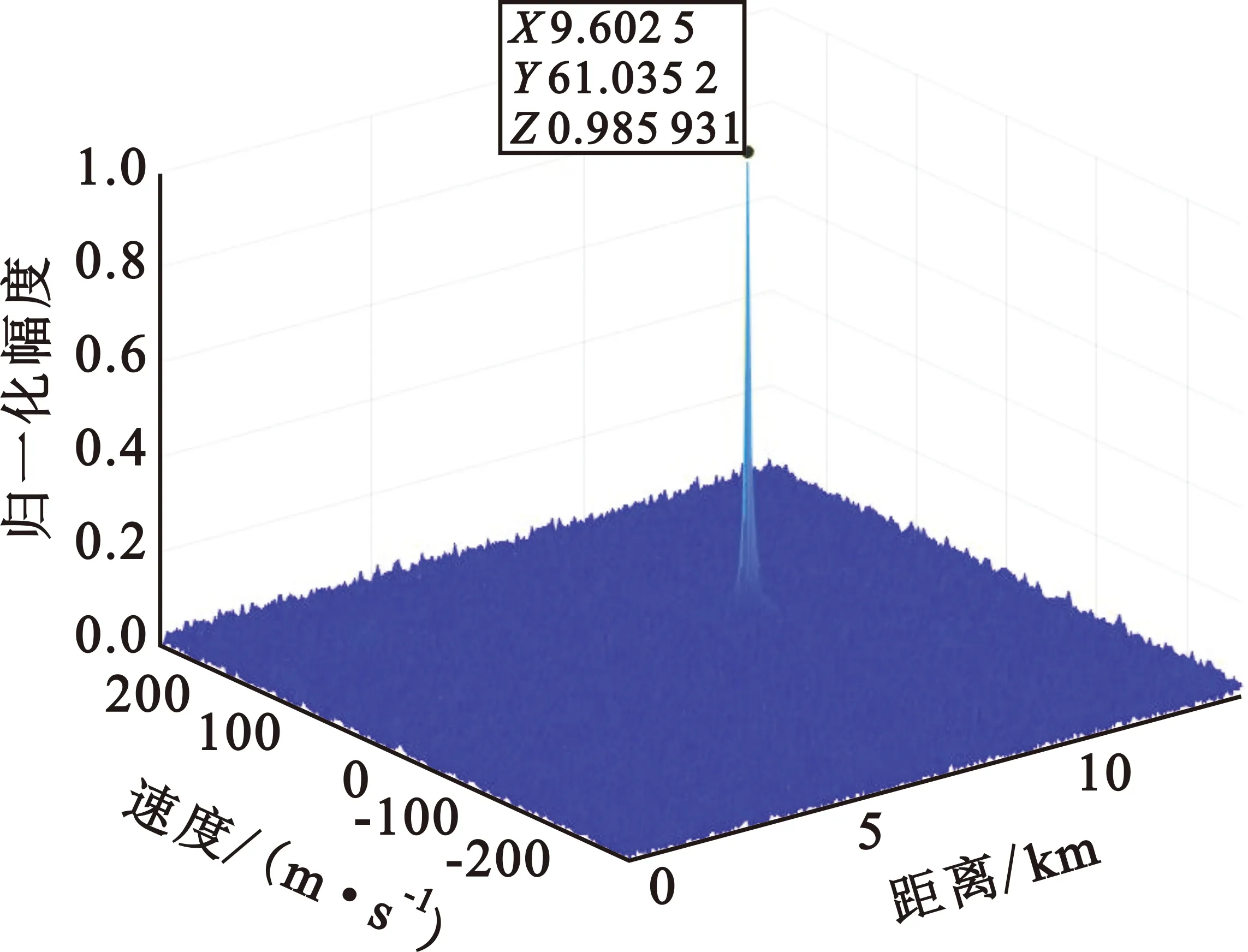
(a)单目标传统雷达MTD图

4.2 双目标

假设有两个目标，目标1的距离为12 km，速度为100 m/s，目标2的距离为26.4 km，速度也为100 m/s，两个目标的回波延时刚好相差一个PRI，回波会发生重叠，此时的回波信号示意图如图8所示，红色虚线为目标1的回波，绿色实线为目标2的回波。

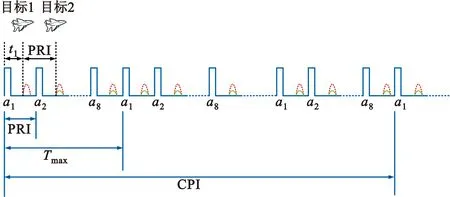
图8 双目标有重叠时的回波示意图

仿真设置信噪比为-15 dB，仍然采用式(19)所示的发射参数，传统PD雷达的MTD图如图9(a)所示，图中只有一个峰值，即传统PD雷达无法分辨有几个真实目标。这是因为两个目标的速度是一样的，并且距离差刚好等于最大无模糊距离，因此在MTD图中两个目标的峰值在同一个位置。而采用本文方法的MTD图如图9(b)所示，图中有两个峰值，说明有两个真实目标，并且计算的距离和速度与设置的距离和速度是一致的，不会产生模糊。

(a)双目标传统雷达MTD图

5 结 论

本文通过高脉冲重复频率的方式发射具有低互相关峰值的脉冲信号，可以同时解决距离模糊和速度模糊问题。传统PD雷达在不改变射频频率的情况下通常无法同时解决距离模糊和速度模糊，增大无模糊速度也就意味着减小了无模糊距离，而本文方法使得PD雷达可以实现远距离无模糊探测，同时不会存在速度模糊。多种仿真结果证明了本文方法的可行性。