混合能源的NOMA网络中最优时延均衡和功率控制算法*
黄 盛
(中国西南电子技术研究所,成都 610036)
0 引 言
非正交多址接入(Non-orthogonal Multiple Access,NOMA)是满足未来无线通信网络的高吞吐量、高密度用户连接数、通信可靠性、能源效率、低时延等网络需求重要技术之一[1-3]。NOMA技术采用叠加编码(Superposition Coding,SC)实现多路信号在相同时域、频域或码域的资源块上传输,为不同的用户提供不同的增益[4]。接收端通过串行干扰消除(Successive Interference Cancellation,SIC)技术分离干扰信号,并提取本接收端的有用信号[5]。在有限的频谱资源下,NOMA技术可有效提升频谱利用率,并成倍增加网络用户容量[6-8]。
随着绿色通信的发展,太阳能、风能、电磁能等可再生能源在通信网络中得到广泛应用。针对可再生能源采集量的振荡特性,为了保持链路通信质量的稳定性,通信网络常采用可再生能源和电能混合供给的方式[9-13]。
功率控制对NOMA技术的性能具有决定性影响,以绿色通信的可持续发展为导引,在混合能源的NOMA网络中的功率控制问题是一个研究热点。此外,通信应用包含在线交互、 视频分享、 在线游戏等多种高实时的时延敏感性业务,单纯最优化吞吐量无法提供良好的时延性能,高效的资源管理不但要提高吞吐量,而且要均衡排队时延的性能。本文致力于研究在混合能源的NOMA网络中联合时延均衡和功率控制的资源管理算法。该资源管理算法综合考虑可再生能源的采集、消耗和储存三者之间的关系,混合能源下多链路调度的功率控制的紧耦合性,以及功率控制在长时间维度上对于时延均衡的影响。与均匀功率控制(Equal Power Control,EPC)算法的对比仿真结果表明,本文提出的联合时延均衡和功率控制(Finite Delay Guaranteed Power Control,FDG-PC)算法在低用户数据包到达率时可有效地降低电能源消耗;在高用户数据包到达率时,同等电能源消耗下,FDG-PC算法可有效地降低数据队列排队时延。
1 系统模型
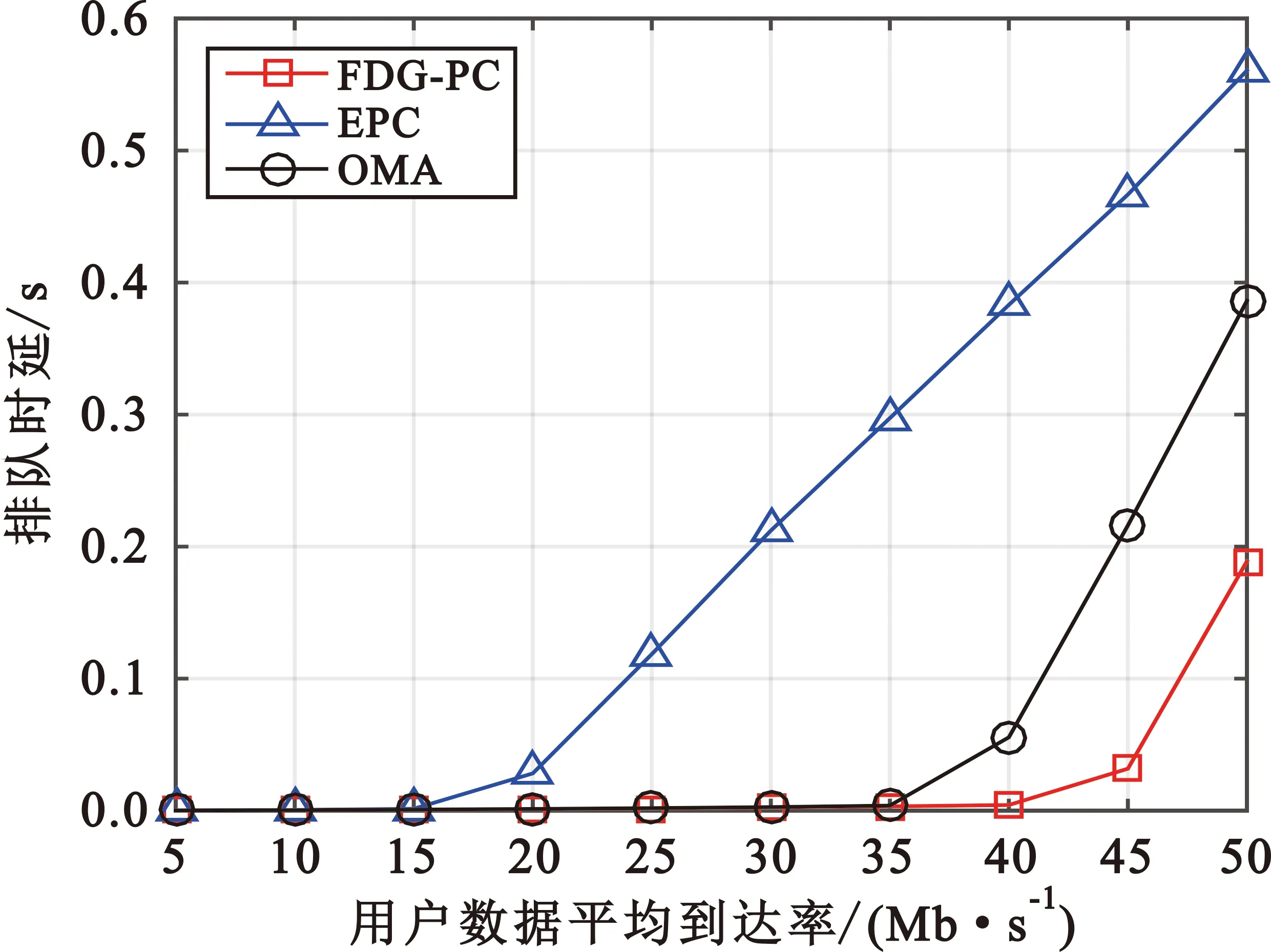
在蜂窝小区内,基站在一个下行链路信道上通过NOMA技术服务两个节点,节点集合定义为U={1,2}。在时域上采用时隙结构,其中时隙t∈{1,2,3,…,∞}。定义时隙t的信道状态为G(t)={gu(t)}u∈U,G(t)在不同时隙上是独立同分布的,gu(t)的取值受路径损耗、多径快衰落和阴影慢衰落影响。每个时隙t内,定义gl(t)=max{g1(t),g2(t)}和gs(t)=min{g1(t),g2(t)}。当g1(t)≥g2(t)时,l=1,s=2;当g1(t) (1) (2) 式中:w为信道带宽;τ为时隙长度;σ2为白噪声功率;Pl(t)为基站在时隙t给节点l发送数据的发射功率;Ps(t)为基站在时隙t给节点s发送数据的发射功率,并且总发射功率需不大于最大发射功率Pmax,即 0≤∑u∈UPu(t)≤Pmax,∀t。 (3) 基站为每个节点u维护一个数据队列。令Qu(t)表示发送节点u在时隙t的数据队列长度。令ru(t)表示时隙t内用户u的到达数据量,服从均值为λu的泊松分布。节点u的数据队列更新方程可定义为 Qu(t+1)=max{Qu(t)-Ru(t),0}+ru(t),∀u∈U。 (4) (5) 为了提升通信效能,基站通过配置可再生能源的储能设备,支持太阳能、风能等可再生能源的采集存储和消耗。将基站的可再能源在时隙t的队列长度表示为W(t),令h(t)表示基站在时隙t内通过能源采集获得的可再生能源数量,服从[0,hmax]的均匀分布。令w(t)表示基站在时隙t内存储或消耗的可再生能源数量。由于可再生能源的储能设备的有限存储容量限制,以及能源存储速率的约束,可将基站的可再生能源的队列更新方程定义为 W(t+1)=W(t)+w(t) , (6) Wmin≤W(t)≤Wmax, (7) wmin≤w(t)≤min{wmax,h(t),Wmax-W(t)} 。 (8) 式中:Wmin和Wmax分别表示最小的储能需求和存储容量上界,而wmin<0 (9) 综上,在保障数据传输时延需求和基站功率限制的约束下,以最小化电能消耗为目标的功率控制随机优化问题可建模为 s.t. 式(3),式(5),式(7)~(9)。 式中:J(t)={[Pu(t)]u∈U,w(t),e(t)}为随机优化问题的控制变量。首先,节点在任意时隙内的传输数据量取决于信道条件和功率控制结果,使得优化问题P1的可行域非凸。其次,网络参数的随机性以及控制变量之间的耦合性,优化问题P1为非凸非线性规划问题,求解该优化问题通常具有较高的时间复杂度。 本节通过李雅普诺夫(Lyapunov)优化方法[15]和凸优化方法[16],依据每个时隙内的网络状态和能源状态进行功率控制,设计了具有多项式时间复杂度的最优时延保障的功率控制算法。 首先,为了满足约束式(5),定义虚拟队列Z(t)的队列长度更新方程定义为 Zu(t+1)=max{Zu(t)+Qu(t+1)-λudu,0},。 (10) 依据队列稳定理论(Rate Stability Theorem)[15],维持队列Z(t)的稳定性等价于满足约束式(5)。 令θ(t)=[Qu(t),W(t),Zu(t)]表示时隙t的队列状态信息,依据Lyapunov Drift定理[15],定义带偏置的李雅普诺夫函数(Perturbed Lyapunov Function)为 (11) 式中:φ(t)为偏置向量(Perturbation Vector),且存在上界φmax。定义单时隙的条件李雅普诺夫偏移(One-slot Conditional Lyapunov Drift)分别为 Δ(θ(t))=E{L(θ(t+1))-L(θ(t))|θ(t)} 。 (12) 随后,根据Lyapunov 优化定理[15],优化问题P1的李雅普诺夫优化函数(Lyapunov Drift-plus-penalty Function)构建为 Δ(θ(t))+VE{e(t)|θ(t)}, (13) 其上界通过定理1给出。 定理1:对于任意的功率控制方法,所有可能的θ(t)和任意的大于零的控制参数V,优化问题P1的李雅普诺夫优化函数式(13)的上界为 E{F(J(t))|θ(t)}+B+ (14) 式中: (W(t)-φ(t))w(t), (15) 2φmax(Wmax+φmax)。 (16) 证明:首先,对更新方程(6)两边同时减φ(t+1),然后取平方、移位、累加等操作后,再依据上下界限制可得 (W(t)-φ(t))w(t)+ 2φmax(Wmax+φmax)。 (17) 其次,对更新方程(4)和(10)两边取平方、移位、累加等操作后,再依据上下界限制可得 (18) (19) 进一步,将不等式(17)~(19)相加,得 2φmax(Wmax+φmax)。 (20) 给定θ(t),对不等式(20)两边同时取条件期望并加上VE{e(t)|θ(t)}可得 Δ(θ(t))+VE{e(t)|θ(t)}≤ (W(t)-φ(t))w(t)|θ(t)}+ max{Qu(t)+ru(t),Ru,max}|θ(t)}。 (21) 式中: 2φmax(Wmax+φmax)。 (22) 依据Min Drift-Plus-Penalty定理[15],对于给定的θ(t),优化问题P1可以转换为最小化上界函数式(14)的优化问题,受限于瞬时约束式(3)和式(8)~(9)。由于上界函数式(14)中最后三项在时隙t内是常数,因此最小化该上界函数的期望等同于根据当前的信道状态信息和队列状信息的情况来最小化该期望内部的函数F(J(t)),可建模为 在初中数学的一题多解的教学中,互动合作交流是实现学生思维交流互动、促进学生多方面探究问题答案的有效形式。例如,在“相似三角形”方面的教学中,相似三角形的判定及其性质是教学难点,它们经常要用于多解题和生活问题的论证和反论证应用方面,考验学生的探究能力。比如,相似三角形有关的题目多为多解题,一个学生一般是思维指向了哪个定理,就按照这个定理去解题,没有要求的话一般不会再去探究新的解题方法。但是不同的学生的解题思维是不同的,因此最终会有许多不同的探究思维。在这种情况下,教师组织起合作学习小组来,目的就是要促进不同解题思维的碰撞和共享,促进学生之间的取长补短,实现每一位学生数学探究能力的拓展和发散。 (Qs(t)+Zs(t))Rs(t)+(W(t)-φ(t))w(t) s.t. 式(3),式(8)~(9)。 由于不同节点的发射功率在传输数据量中存在相互耦合关系,因此优化问题P2的目标函数为非凸函数,使得优化问题P2的求解方法通常具有指数级别的时间复杂度。为了设计具有多项式级别复杂度的功率控制算法,本节通过分析优化问题P2的KKT条件[16],解析两个节点的最优发射功率之间的关系,根据拉格朗日乘子的取值确定Pl(t)或Ps(t)最优解,将该最优解代入优化问题P2可得关于其他控制变量的凸优化问题P3 ,即优化问题P2的最优解可通过求解凸优化问题P3在三种不同参数取值下的最优解来获得,如定理2所示。 定理2:定义凸优化问题P3为 wτlb(1+Px(t)φ1(t))+(W(t)-φ(t))w(t) s.t. 0≤Px(t)+φ2(t)≤Pmax, wmin≤w(t)≤min{wmax,h(t),Wmax-W(t)}, τPx(t)+w(t)-e(t)≤h(t)-τφ2(t)-C(t)。 其中,{x,φ1(t),φ2(t)}的三种参数取值分别为 (23) (24) (25) e(t)=e(1)(t)}, (26) e(t)=e(2)(t)}, (27) w(t)=w(3)(t),e(t)=e(3)(t)}。 (28) 证明:依据KKT条件定义,优化问题P2中Pl(t)和Ps(t)的最优解满足KKT条件式(29)~(34)。 (29) (30) λlPl(t)=0, (31) λsPs(t)=0, (32) υ(Pl(t)+Ps(t)-Pmax)=0, (33) α(τ(Pl(t)+Ps(t))+C(t)+w(t)-h(t)-e(t))=0。 (34) (35) 进一步推导可得Pl(t)的最优解为 (36) 定理3:定义偏置向量φ(t)=Wmin-wmin+V,则在优化问题P2取得最优解J*(t)的功率控制下,可再生能源的队列状态W(t),∀t,始终满足最小储能需求和存储容量上届约束。 证明:在优化问题P2取得最优解J*(t)时,当W(t)>φ(t)时,w(t)的最优解为w*(t)=wmin;当W(t)-φ(t) 基于可再生能源的队列更新方程(6),当W(t)∈[Wmin,Wmin-wmin)时, W(t+1)=W(t)+min{wmax,h(t),Wmax-W(t)}≥W(t)≥Wmin, W(t+1)=W(t)+min{wmax,h(t),Wmax-W(t)}≤Wmax; 当W(t)∈[Wmin-wmin,Wmax]时, W(t+1)=W(t)+w(t)≥W(t)+wmin≥Wmin, W(t+1)=W(t)+w(t)≤W(t)+Wmax-W(t)=Wmax。 依据Min Drift-Plus-Penalty定理[15],虚拟队列式(10)是稳定的,从而满足了时间平均上的有限队列长度约束式(5)。 其次,定理3证明了本文提出的有限时延保障的最优功率控制方法(FDG-PC)能够保障可再生能源储存约束式(7)。本节通过Matlab仿真验证FDG-PC方法在电能消耗和时延保障上的性能,并采用均匀功率控制(EPC)方法和在最优时延均衡和功率控制算法(Orthogonal Multiple Access,OMA)技术下的OMA进行性能对比。 EPC方法对优化问题P2通过设置Pl(t)=Ps(t)=0.5Pmax进行凸优化松弛,并通过内点法求解w(t)和e(t)的最优解,具有多项式级别复杂度。 OMA方法的功率控制中要求Pl(t)=0或Ps(t)=0,该方法的时延均衡和功率控制的最优解为凸优化问题P3在式(23)和式(24)两种参数取值下的最优解,具有多项式级别复杂度。 用户1和用户2分别在以基站为中心、半径为125 m和200 m的圆环上随机分布。主要仿真参数配置如表1所示,路径损耗模型采用PL=128.1+37.6lbd,其中路径距离d的单位为km。多径快衰落服从相互独立的均值为1的指数分布,阴影慢衰落模型采用标准方差为8 dB的独立对数正态分布。在仿真中,数值结果为50次拓扑生成且每个拓扑运行2 000个时隙所获得的平均值结果。 表1 仿真参数配置 令V=1并设置用户数据包平均到达率为5~50 Mb/s,图1给出了NOMA中电能源消耗与用户数据包平均到达率的关系。EPC算法由于采用均匀功率控制,每个时隙采用固定的发射功率,因此在时间平均上的电能源消耗不随着用户数据包平均到达率而变化。随着用户数据包平均到达率逐渐增加,FDG-PC算法通过增大发射功率的方式提高网络吞吐量,以保障数据队列的排队时延均衡在有限范围内,从而使得电能源消耗逐渐增加。当用户数据包平均到达率大于等于40 Mb/s时,FDG-PC算法在每个时隙的发射功率基本达到最大发射功率上限,因此电能源消耗趋于稳定值;当用户数据包平均到达率为15 Mb/s时,FDG-PC算法的电能源消耗为EPC算法的电能源消耗的42%。此外,虽然FDG-PC算法和OMA算法中电能源消耗随着用户数据平均到达率的变化趋势相同,但是FDG-PC算法利用NOMA技术中串行干扰消除带来的性能增加,在相同用户数据平均到达率下可有效地降低电能源消耗。 图1 电能源消耗与用户数据平均到达率的关系 图2描述了NOMA中排队时延与用户数据包平均到达率的关系。当用户数据包平均到达率较低时,网络吞吐量远大于用户数据包到达率,FDG-PC算法和EPC算法的排队时延均稳定于低时延状态。随着用户数据包平均到达率逐渐增加,用户数据包需在数据队列中缓存一段时间才能获得传输机会。当用户数据包平均到达率大于15 Mb/s时,EPC算法的排队时延开始逐渐增大。而FDG-PC算法采用最优的时延均衡和功率控制,在保持较低的电能源消耗的同时,能够提供较高的网络吞吐量,使得FDG-PC算法的排队时延在用户数据包平均到达率大于40 Mb/s才开始逐渐增大。此外,相比于OMA算法,FDG-PC算法能够有效地提升用户的吞吐量性能,减少用户数据包在数据队列中的排队等待时间,从而维持更好的排队时延性能。在用户数据包平均到达率为50 Mb/s时,FDG-PC算法的排队时延比EPC算法和OMA算法的排队时延分别小0.37 s和0.19 s。 图2 排队时延与用户数据平均到达率的关系 针对混合能源的NOMA网络,考虑数据包到达的随机性、多能源均衡需求以及控制变量的时间耦合性,本文提出了一种具有多项式级别复杂度的最优时延均衡和功率控制算法,以期最小化电能源消耗,并满足有限排队时延与基站功率约束。仿真结果表明,本文提出的FDG-PC算法能够降低电能源消耗,并有效地均衡数据队列的排队时延。此外,在M个用户的多用户场景下,可采用以时帧为周期的定时结构,每个时帧包含N(N≥M/2)个时隙,遵循每个时隙服务2个节点的约束进行用户配对,本文提出的FDG-PC算法可拓展至优化每组配对的两用户在多个时帧内的时延均衡和功率控制。

2 单时隙的有限时延保障的最优功率控制






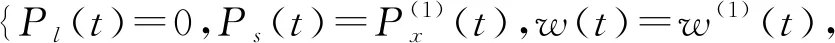

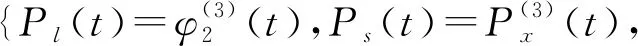


3 仿真结果与数值分析
3.1 仿真设置

3.2 仿真结果

4 结 论

