强噪声下非平稳时延目标信号提取*
葛双超,王梦蕾
(中北大学 仪器与电子学院,太原 030051)
0 引 言
由于受各类环境和人为干扰,电磁测试信号往往包含大量噪声,特别是随着各领域对测试精度要求的不断提高,复杂环境下微弱有效信号提取逐渐成为一个重点研究课题。
现实中各种信号普遍存在时域突变性,且频谱成分复杂,属于非线性、非平稳信号。1998年,Huang等人[1]提出了Hilbert-Huang变换(Hilbert-Huang Translation,HHT),其核心算法为经验模态分解(Empirical Mode Decomposition,EMD)。该方法可以将信号分解为一系列本征模函数(Intrinsic Mode Function,IMF),对有效IMF进行Hilbert变换可获取有效信号参数信息,但是EMD方法在强噪声下存在端点效应和模态混叠的问题。变分模态分解(Variational Mode Decomposition,VMD)是Dragomiretskiy等人[2]在2014年提出的一种非递归的自适应、准正交的模态变分和信号处理方法。VMD 算法通过迭代搜索自适应地匹配各个模态分量的最佳中心频率和有限带宽,在搜索和求解过程中实现IMF的有效分离,进而实现目标信号成分提取。VMD 算法已成功用于机械故障诊断、地震记录分析等领域的非线性、非平稳信号处理,但是其过度惩罚了域边界和内部的跳跃,强噪声下无法有效处理信号的时移偏差[3]。奇异谱分解(Singular Spectrum Analysis,SSA)算法[3]是一种全局分析法,利用相空间重构的基本思想,通过奇异值分解对原始信号不同成分进行提取,该方法在轨道矩阵长度和分解层数设置合理的情况下可以有效分离时域差异较大的周期信号。2018年,Harmouche等人[4]将SSA与无监督分类算法相结合,提出了滑动奇异谱分析法,可有效提取两个频率相近的正弦信号。
上述算法处理具有时延不定特性的非平稳信号时,普遍存在局部特性向全局扩散等问题。对于上述问题,直接的解决方案是将信号分解成较短的数据块,使这些分段信号具有短时局部平稳特性。因此本文针对数据自动分段和参数提取问题进行了相关研究,构建了时延信号相干检测模型并在此基础上利用VMD算法设计了自适应匹配滤波器进行强噪声下时延信号提取。
1 时延信号相关检测模型
1.1 相关检测定位算法原理
相关检测技术是一种很强的周期信号提取方法,该技术利用信号和噪声、不同成分信号间的不相关性,对目标信号进行分离[5]。本文利用互相关函数包络和峰值梯度为特征值构建时延信号相关检测模型进行目标信号自动分段提取。
设原始采样序列x(t)由两部分组成,x(t)=xn(t)+s0(t),其中,xn(t)为非线性、非平稳信号;s0(t)为x序列中的目标信号,
(1)

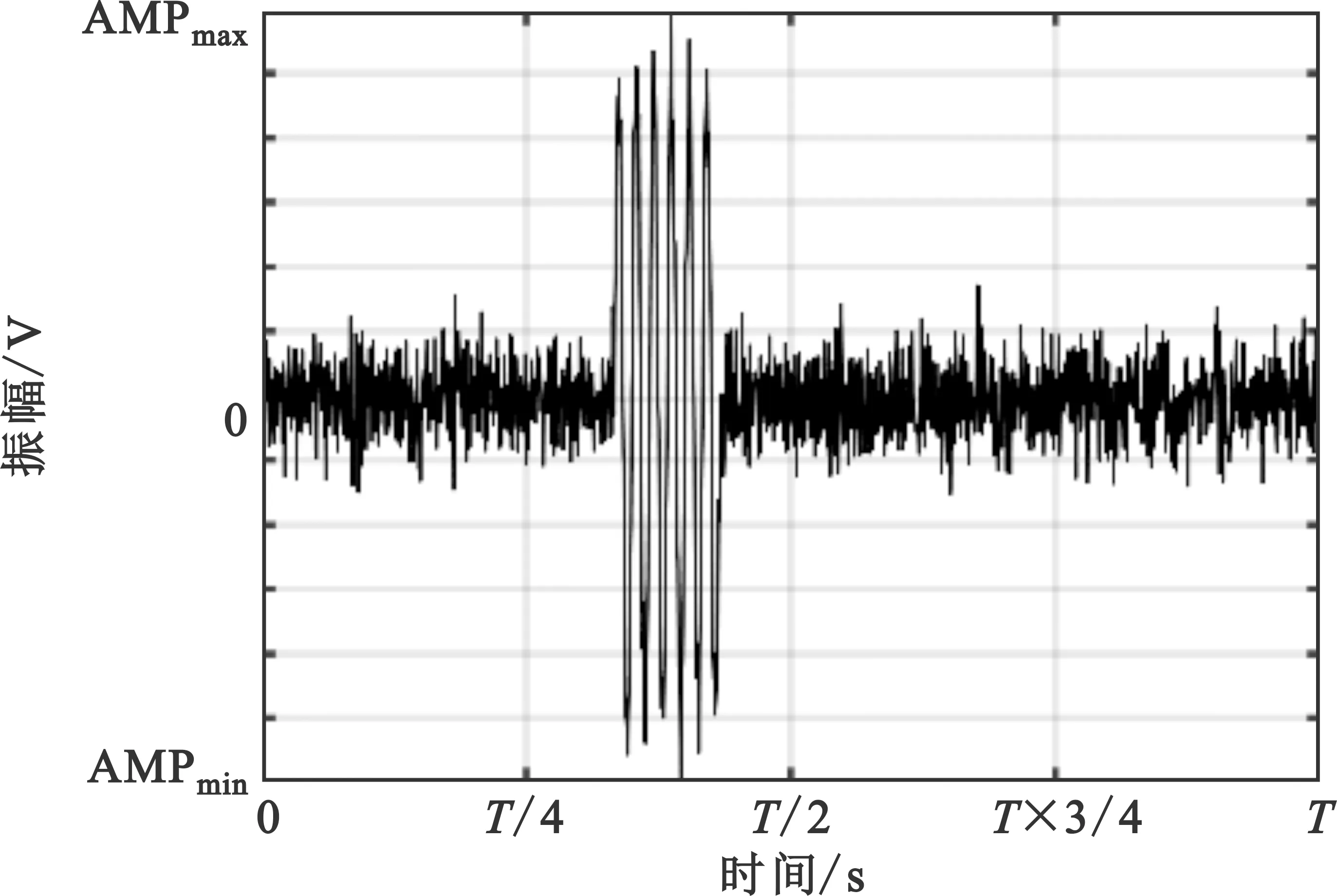
(a)原始信号x
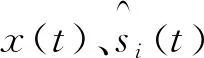
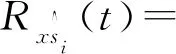

(2)
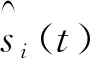
(3)
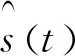
(4)
式中:L1和L2分别为目标信号在原始序列中的起始位置;N为原始数据序列长度N=fs×T,fs为采样率;L0为标准正弦信号长度,L0=fs。
以上即为相关检测定位算法的基本原理,计算过程如图2。

图2 互相关检测定位算法计算过程
实际应用中由于式(2)中第一项并非绝对为0,所以采用最大峰值梯度为特征参数,互相关函数包络梯度Δp由式(5)给出:
Δp(i)=Penv(i)-Penv(i-1)。
(5)
式中:Penv(i)表示坐标点i处的互相关函数包络值。在i=L1处出现互相关函数最大峰值梯度。
1.2 目标数据段自截取算法
利用软阈值对互相关函数有效包络线进行提取。互相关函数理想包络范围由下式给出:
(6)
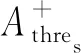
(7)
式中:nshift为偏移因子,⎣」表示向下取整,[l1l2]为有效包络窗口边界,max()和min()分别为最大和最小值函数。取最大最小的目的是保证可完整提取出目标信号段。
利用上述相关检测定位算法可以初步确定目标信号s0i在序列x中出现的起始位置L1和目标信号序列长度L。对多频信号的提取重复执行上述算法即可。
利用单频仿真信号测试上述算法,结果如图3所示。
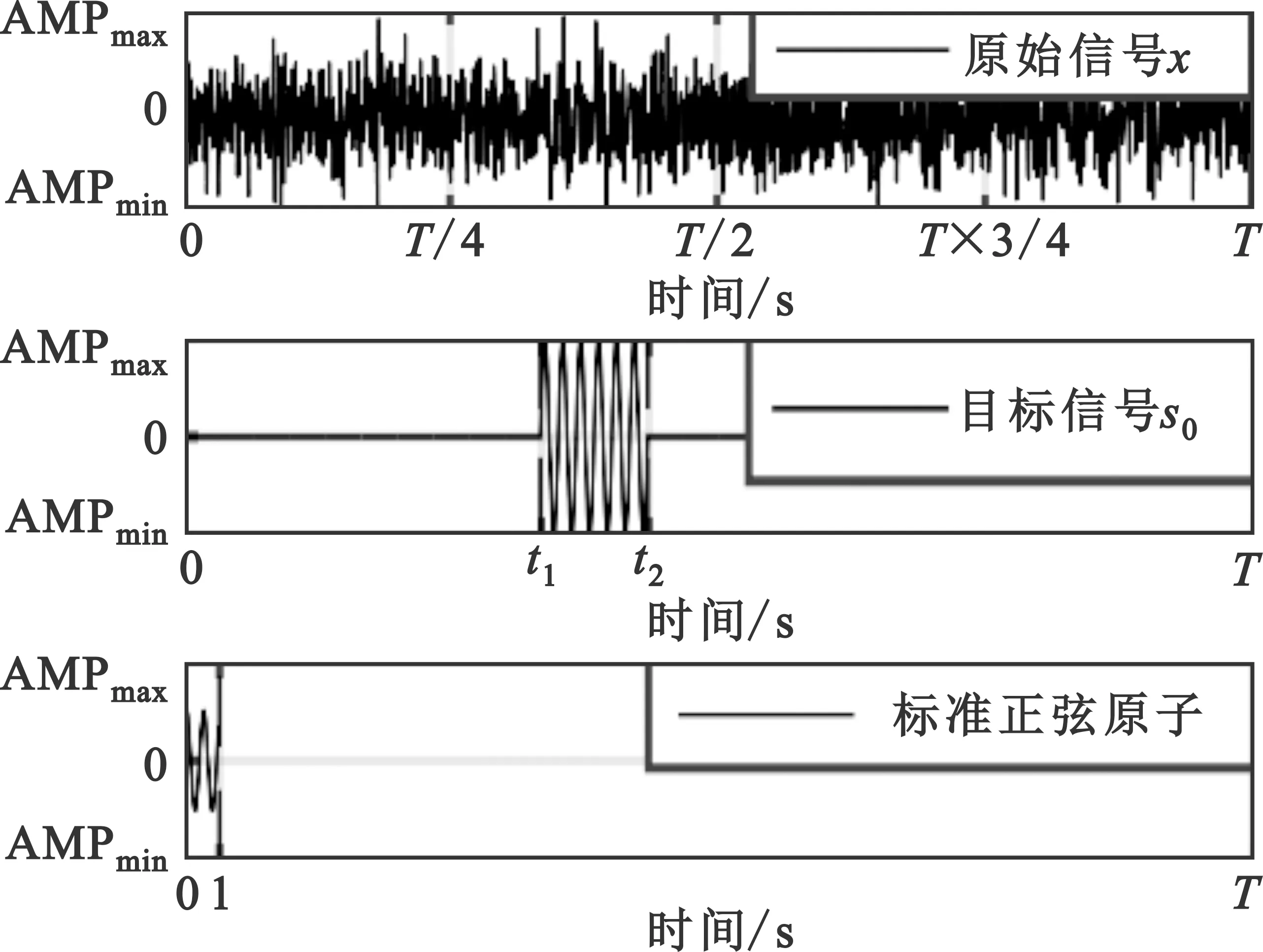
(a)时域波形
获取的目标数据段时频参数如表1所示。

表1 相关检测定位算法处理结果

利用上述算法截取含目标信号数据段后,再利用VMD算法对截取的信号进行分解即可获取目标信号。
2 基于变分模态分解算法的自适应匹配滤波器
2.1 变分模态分解算法原理简介
VMD算法的实质是将一个复杂的实信号xs(t)分解为K个具有特定稀疏性的相互独立子信号uk(变分模态分量),在K值设置合理的前提下VMD可有效地消除信号分解时所存在的模态混叠和端点效应现象[7]。VMD算法分为两个过程,分别为构造约束变分模型和求解约束变分模型。
进行约束变分模型构造时,首先将模态分量函数uk(t)进行希尔伯特变换以获取其相应的解析信号,再计算解析信号得到单边频谱
(8)
式中:δ(t)为冲激函数。
然后将模态分量函数的解析信号与指数ejωkt相乘来估计中心频率ωk,通过频移将模态函数uk(t)的频谱调制到相应的基频带
(9)
通过对解调信号进行高斯平滑来估计uk(t)的带宽,得到相对应的约束变分模型表达式为
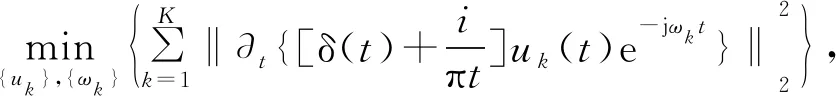
(10)
式中:min{ }为取最小值函数,K为预先设定的分解个数,Fx为原始输入信号的频域实值信号。
式(10)是一个最优化问题,求解时引入二次惩罚因子α与增广拉格朗日乘子λ,将目标函数的约束变分问题转变为非约束变分形式,从而得到相应的拉格朗日函数表达式:

(11)
式中:L(·)表示增广拉格朗日函数;〈·,·〉表示内积;二次惩罚因子α是控制数据保真度的均衡参数,用于平衡变分正则项和二次约束项,在含噪声情形时可保证信号重构精度;λ可以保证模型约束条件的严格性。
利用Lagrange法的交替方向乘子求公式(11)所述变分问题的最优解,从而将原始信号分解为K个IMF分量。
2.2 自适应匹配滤波器参数预设方法

2.3 自适应匹配滤波模态自动筛选方法
从VMD算法分解出的K+1个分量中确定有效信号是VMD算法的一个关键问题。本文利用自截取信号的K个主峰频率[f1f2,…,fK]与VMD算法分解获取的K+1个主频[ω1ω2,…,ωK+1]自动筛选有效分量。算法伪代码如下:
1 初始化:构造K×N的s数组并初始化为0,s=zeros(K,N)
2 令i=1
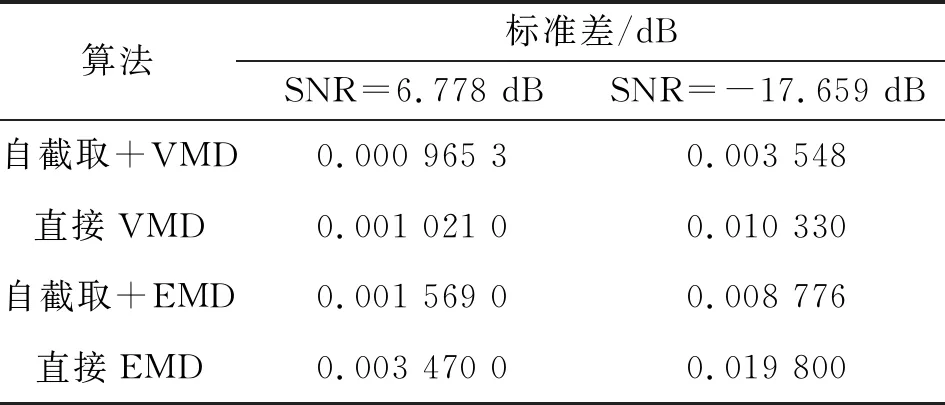
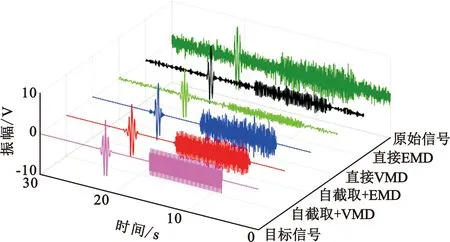
3 While (i fort=1:K+1 if(ωt==fi) break end end si(L1:L2)=u(t)筛选出第i个有效分量 end 通过上述自适应模态匹配筛选方法,既可以获取目标数据段内的单个有效信号分量,同时可获取多频叠加信号。 本文所述算法整体流程图如图4所示。 图4 非平稳时延目标信号提取流程 算法主要步骤如下: 输入:原始信号x。 Step1 构造时延信号集合S,令S=∅。 Step2 利用1.2节所述自截取算法提取目标数据段xs=x(L1:L2)。 Step3 利用本节所述基于变分模态分解算法的自适应匹配滤波器对数据段xs进行信噪分离处理,提取有效信号u1,u2,…,uK。 Step4 构造0值序列集合s={s1,s2,…,sK}=zeros(K,N),其中N为原始序列长度,并令si(L1:L2)=ui。 Step5 更新数据: Step6 判断更新后的x序列是否存在特殊频点,判断标准为振幅谱曲线峰值显著大于谱线均值。如果存在特殊频点则执行Step 2,否则执行Step 7。 Step7 输出S。 利用Matlab仿真构造了由非平稳噪声信号和单频时延目标信号叠加而成的原始信号x1: (12) 式中:ns1为高斯白噪声;s1为时延正弦信号,采样率为150 Hz,采样时间30 s;wgn为非平稳噪声信号;f=2 Hz为正弦信号频率; [t1t2]=[10 13]为正弦信号出现时段;φ=0为相位;A为振幅。信号x1可模拟超声波测试中的回波信号等探测信号。 高信噪比下A=5 V,SNR=6.778 dB。分别利用直接EMD算法、直接VMD算法、目标信号段自截取后EMD算法和目标信号自截取后VMD算法对目标信号进行提取。高信噪比下不同算法目标信号提取结果如图5所示。 (a)不同算法提取结果 为进一步突出不同算法的信号提取效果,降低原始信号信噪比,令A=1 V,SNR=-17.659 dB,信号时域波形如图6(a)墨绿色曲线所示。利用四种算法进行了分析对比,结果如图6所示。 (a)不同算法提取结果 仿真结果表明,不同信噪比情况下,目标信号段自截取后VMD算法提取的信号均具有最高精度,直接EMD算法提取精度最低。不同信噪比下不同算法处理结果的统计分析见表2。 表2 不同算法误差统计分析对比 为进一步验证本文所述方法的有效性,利用高斯噪声和多个目标信号混叠构造了如下仿真数据: x2=ns2+s2=ns2+s21+s22= (13) 其中,信号采样率为100 Hz,采样时间30 s,SNR=1.53 dB。目标信号双频信号s21出现时刻为5~15 s,由频率为5 Hz和25 Hz的正弦信号叠加构成;目标信号s22出现时刻为20~22 s,为morlet小波。信号x2与电力系统故障检查中的常见振动和局部充放电信号类似。 对s21和s22信号的自截取结果如图7所示。 (a)目标信号s21自截取结果 (a)不同算法提取结果 对不同算法提取结果进行了误差分析和效率对比,结果见表3。 表3 强噪声下复杂信号不同算法误差统计分析对比 表3表明,自截取+VMD算法对于混叠在背景噪声中的复杂目标信号提取效果最好。由于原始数据中混叠两个时段的不同类型的目标信号,而自截取+VMD算法分别对这两段目标信号进行了提取,故用时较其他算法偏长。直接对整段数据进行处理虽然用时较短,但是提取结果存在明显的模态混叠现象,且无法对两段目标信号进行有效区分,因此提取数据的利用价值不如本文所述方法高。 分段提取方法是一种有效的强噪声下时延目标信号分析方法。本文提出了时延信号自截取算法,并设计了基于VMD算法的自适应匹配滤波器对自截取信号段进行处理来获得目标信号。结果表明,高信噪比时,直接对整段数据进行VMD变换可提取时延目标信号,误差略大于本文提出的方法,在对精度要求不高、实时性要求较高的场合可采用直接VMD;当背景噪声较强,完全淹没目标信号时,直接VMD会将局部目标信号放大至整个时间过程,不能有效识别局部时域细节信息,而直接EMD算法几乎失效,这种情况下需采用目标信号段自截取后自适应匹配滤波算法进行目标信号提取。 当原始信号仅包含单一时延目标信号,本文所述方法的处理时间稍高于直接VMD算法,满足实时性要求;当原始信号成分复杂、包含多个不同时延的目标信号时,本文所述方法会对原始信号进行多次迭代处理,相应的处理时间会有所增加,最终可依次提取各个时延信号;而传统方法虽然效率稍高于本方法,但无法有效区分不同时延的信号成分。因此,本文所述方法对于复杂信号的分解效率高于传统方法,可为后续的处理提供更有价值的数据。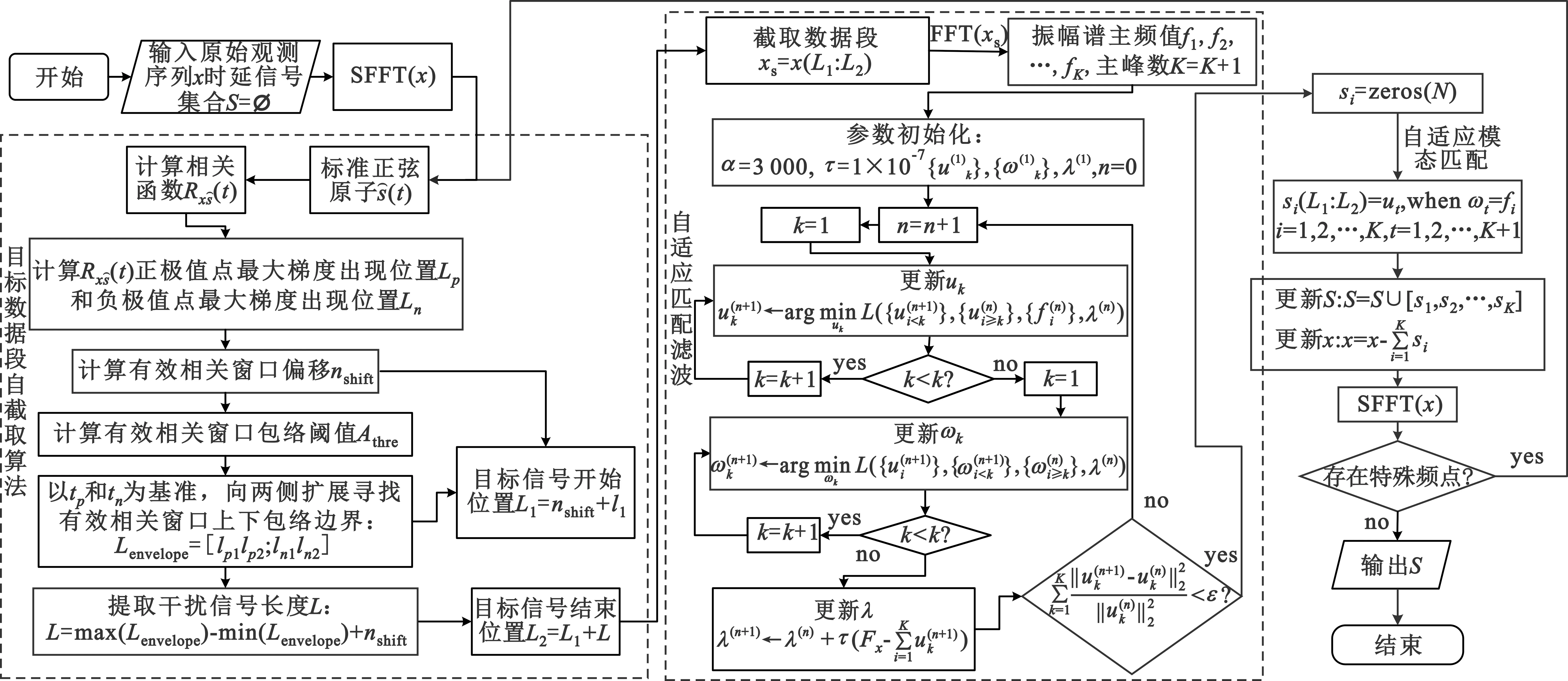
3 实验与分析




4 结 论

