基于改进小波阈值法的MEMS 陀螺仪信号降噪研究*

于航 王 直 董 勃 刘博

（江苏科技大学 镇江 212003）

1 引言

在工业制造领域，汽车发动机等要求预紧力充足且均匀的关键螺纹连接位置需要采用扭矩转角法装配［1］，由此对扭矩扳手提出了一个新的要求：具备测量角度的功能。在设计具备可测角度功能的扭矩扳手的课题中选用了基于微机械电子系统（MEMS）技术的陀螺仪传感器进行角度测算。MEMS 陀螺仪以其低成本、低功耗、体积小和质量小等优势在汽车导航、姿态解算等领域被广泛的应用，然而微加工技术与集成工艺技术的限制和使用过程中外界环境多变等因素使得MEMS 陀螺仪的输出信号检测不准确，MEMS陀螺仪的发展前景被其精度低、噪声高的缺点严重制约，如何高效降噪，提高陀螺仪输出信号的精度这一难题亟待解决［2］。

MEMS 陀螺仪的误差来源分为确定性误差和随机性误差，随机误差显著地影响着惯性传感器的性能，这种误差不能够完全消除，只能通过算法对其抑制减小。目前针对随机误差的算法较多，其中，杜瑾等人推导了不同阶数拟合曲线的回归方程，对各阶数的补偿效果进行对比，选取了4 阶多项式曲线拟合，证实了该补偿方法对降低MEMS陀螺仪的随机误差有效［3］。纪涛等结合EMD 分解完全自适应和VMD 分解对噪声不敏感的优点，对陀螺仪随机误差进行去噪，匀速实验下信号的均方根误差得到有效减小［4］。马群等运用Allan 方差分析法对陀螺仪随机误差成分进行辨识，建立自回归滑动平均（ARMA）模型，并根据模型参数设计了卡尔曼滤波器，结果表明：卡尔曼滤波器能有效减小噪声系数，提高输出精度［5］。

2 信号的误差分析与降噪处理

2.1 MEMS陀螺仪的误差分析

影响陀螺仪精度的随机性误差包含量化噪声、角度随机游走、速率随机游走、零偏不稳定性等几个部分［6］。其中量化噪声一般是由模数转换时的量化误差产生，属于高频噪声，能够通过低通滤波器处理。角速率随机游走、零偏和零偏不稳定是制约MEMS陀螺仪应用的关键因素，其中角速率随机游走在初期有增长趋势，之后相对稳定，而零偏不稳定误差波动范围较大，主要由电路的不稳定造成。减少陀螺仪的随机漂移是陀螺仪降噪的重点。

2.2 改进小波阈值函数去噪

小波分析是一种被广泛运用于信号处理领域的时频分析方法。小波去噪的方法有多种：小波分解与重构法去噪、非线性小波变换阈值法去噪、平移不变量小波去噪、小波变换模极大值法去噪。考虑MEMS 陀螺仪的输出信号是以低频为主的非平稳信号，且阈值法具有计算速度快、能得到原始信号的近似最优估计的优点，选用阈值法去噪更为合适［7］。小波变换阈值法去噪的原理为：含有噪声的信号经过若干层小波分解，提取各层高频小波系数。有用信号对应的小波系数幅值较小，噪声对应的小波系数幅值较大，由此可以选择一个适合的阈值T 对各层小波系数进行阈值处理，保留小于阈值T 的系数，去除高于阈值T 的系数，最后，这些经过阈值处理的小波系数将通过小波逆变换进行重构，得到去噪之后的信号［8］。阈值过大则损失部分有用信息，阈值过小则去噪不充分。此外，阈值函数的选取对重构信号的平滑度产生影响。传统的阈值函数分硬、软阈值函数两种。硬阈值函数表达式为

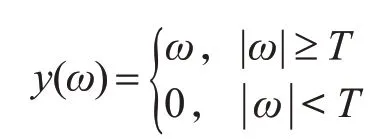
软阈值函数表达式为

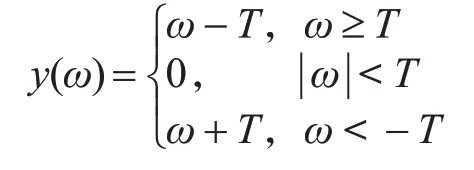
式中ω为经过小波分解前含噪信号的小波系数，T 为小波阈值，y(ω)为经过阈值函数处理后得到的小波系数。采用硬阈值函数处理后的信号可以保留信号边缘等局部特征，更加接近原始信号，但是去噪不连续，在信号重构时容易出现伪吉布斯现象。采用软阈值函数处理后的信号比较光滑，但是在去噪的同时也会去掉部分有用信号［9］。本文提出了一种改进的阈值函数，函数表达式如下：

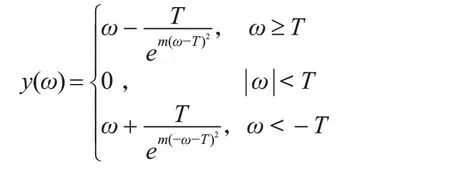
其中m 为可调节参数，选取不同的m 值，可以增强阈值函数的自适应性，在实际使用过程中更加灵活。当m=0 时，函数为软阈值函数，当m 趋近于无穷大时，函数趋近于硬阈值函数。新阈值函数在±T 处是连续的，可以解决硬阈值函数带来的伪吉布斯现象，也可以缓解软阈值函数与真实数据存在恒定偏差的问题。图1为各阈值函数曲线图。

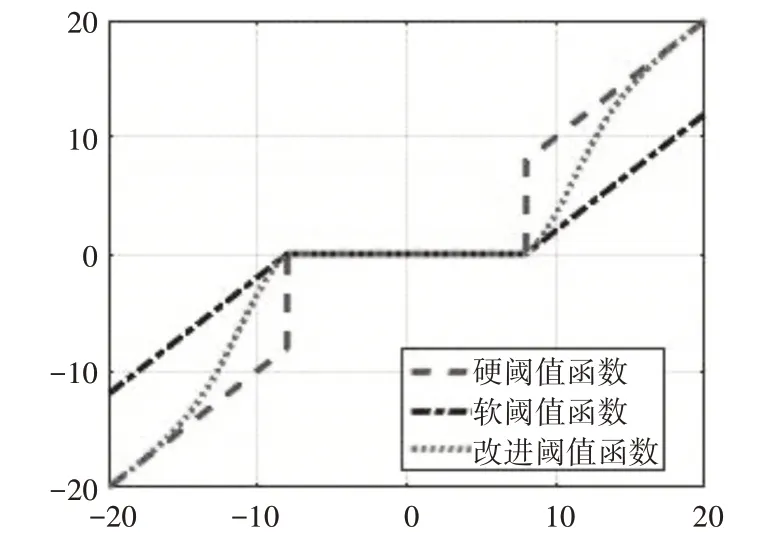
图1 各阈值函数曲线图

小波阈值选用通用阈值：

其中，N 为信号长度，σ为噪声方差，Donoho 和Johnstone给出了噪声方差的估计：

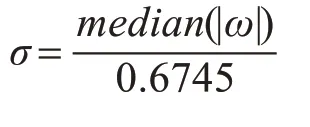
3 仿真验证

3.1 角速度信号获取

构建数据采集系统时选用了InvenSense 公司生产的MPU6050 惯性传感器，通过与STM32 系列单片机相连，向上位机发送数据。MPU6050 集成了3 轴MEMS 角速度和3 轴MEMS 加速度计，可读取的三个角度分别是俯仰角（Pitch）、偏航角（Yaw）和滚轴角（Roll）。在扳手的使用过程中，一般情况下，我们要读取的角度是偏航角（Yaw）。本文以实际静态测量MEMS 陀螺仪Z 轴角速度信号为例，在静态条件下，以一定采样率对MPU6050 实际输出角速率进行采样，得到陀螺仪的原始输出数据。使用Matlab软件处理从KEIL 软件中获取的陀螺仪数据，以此验证改进后的阈值函数对信号去噪的有效性。

3.2 仿真结果与分析

选取的小波基、分解层次也是影响去噪能力的重要因素。选择与被分析信号相似度高的小波基函数是解决问题的首要步骤，选取合适的小波基可以减少计算量和信号重构时的失真［10～11］。dbN、symN、biorNr.Nd 和coifN 是工程中常用的小波基函数族，这几族小波基都具备良好的正交性、紧支撑性。孙玮指出在以上四族小波基中，db6、sym4、bior3.3 和coif3 分别为各小波系中最适应MEMS 陀螺仪信号的小波基函数代表［12］。小波分解层数越大，信噪分离越彻底，但是到了一定层数时，去噪效果变化不明显，伴随而来的是计算量大，程序处理时间长，失真导致的重构误差大［13～14］。综合考虑去噪效果和数据处理时间，本文确定小波分解层数为4层。本文分别用db6、sym4、bior3.3和coif3四个小波基对采集到的信号进行4 层小波分解，改进后阈值函数的可调节因子m 取0.01，重构后的信号信噪比和均方根误差数据如表1 所示，数据显示改进阈值函数处理后的信号信噪比和均方根误差优于传统硬、软函数的处理结果。比较数据可得出：针对MEMS 陀螺仪输出信号，选取sym4 为小波基函数比较适合。

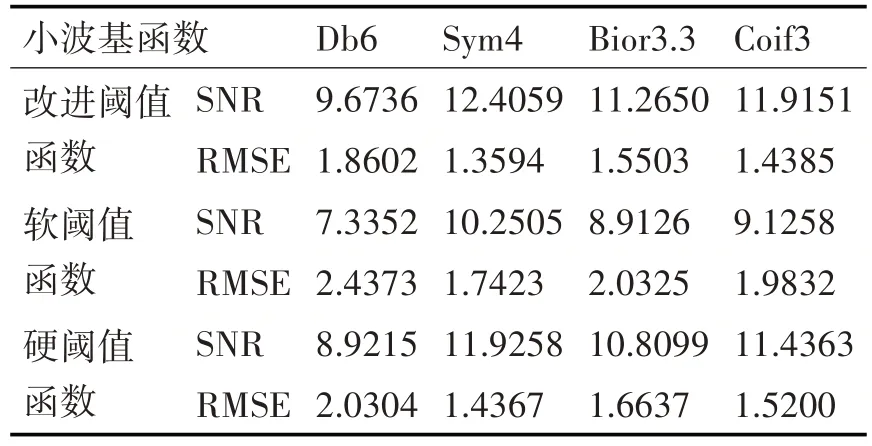
表1 数据对照表

以sym4 为小波基函数，经过4 层分解后，未经处理和经过不同的阈值函数处理后的信号曲线如图2 显示。由图像波形可以看出，改进阈值函数处理后的信号波形去噪效果明显，对比起硬阈值函数的曲线，改进后的曲线更加平滑，对比起软阈值函数的曲线，改进后的曲线保留了原始信号的特征尖峰点。

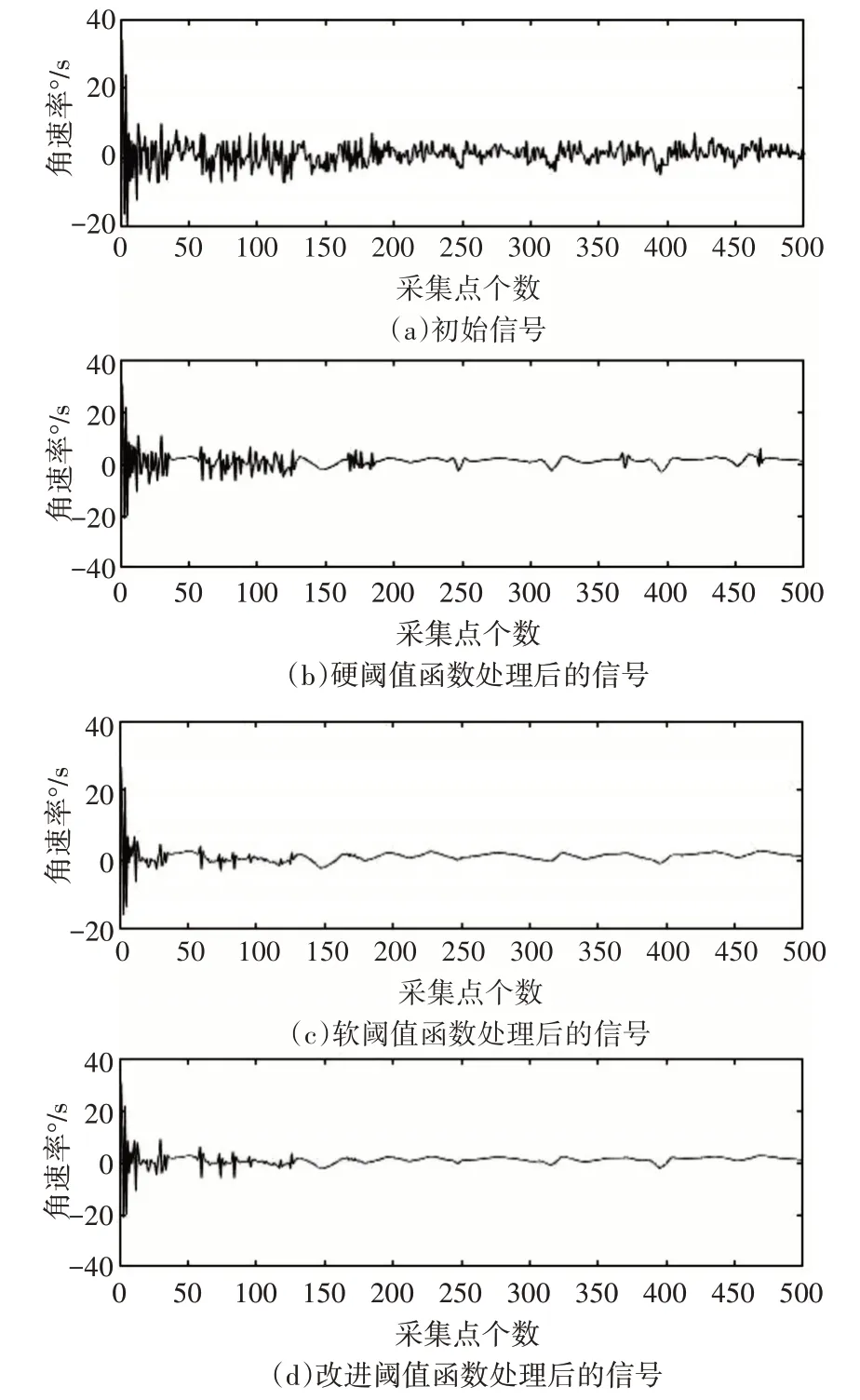
图2 改进前后信号曲线图

4 结语

本文以实际静态测量的MEMS 陀螺仪Z 角速度信号为例，选取了sym4 为小波基对原始信号进行4 层小波分解，改进了阈值函数，对信号进行去噪和重构，通过信噪比和均方根误差对去噪后的信号进行分析对比，实验结果表明：改进后的阈值函数可以保留传统软、硬阈值函数的优点，可调节因子的引入具有更高的自适应性。本文提出的改进阈值函数去噪方法可以直接处理MEMS陀螺仪零漂，对以后的动态去噪研究也有着重要的启发意义［15］。