ACOSA：一种基于MapReduce 的启发式调度算法*

贺立 戴新发 夏静

（武汉数字工程研究所 武汉 430205）

1 引言

在信息化时代，互联网产生的数据量呈爆炸性增长，而如何高效处理这些数据以提供高质量服务成为当前面临的关键问题。针对该问题，互联网发生了一次重大变革，即云计算的出现。MapReduce［1］是一个编程模型，也是一个处理和生成超大数据集的算法模型的相关实现。Hadoop［2］是MapReduce的开源实现，它不仅广泛应用于批量大作业同时也用于处理相应低效率的短作业。

现有的MapReduce 调度算法存在许多问题。比如FIFO 调度算法相对简单、便于理解、易于实现。若单个作业发送到集群，则该作业会将整个集群资源占据；若多个作业发送到集群，则调度器基于作业的发送顺序完成作业调度。虽然所有用户共享整个集群资源，但FIFO 给用户提供资源的机会并不公平，所以FIFO 调度器在实时调度处理方面并不适用。Fair 算法调度器给所有用户都分配了独立资源池以确保公平性。因此，不管某用户提交多少作业，都不会影响到其他用户的资源池，所有用户都可以得到相同的共享资源，但无法保证所有节点负载均衡；资源的利用率不高。Capacity 算法队列设计层次化；弹性分配；容量保证；可操作性高但不支持不支持负载均衡和抢占。

根据现有调度算法的缺点，本文提出了一种基于ACO 和SA 的组合优化算法——ACOSA 算法，该算法可以结合了ACO 算法和SA 算法在调度算法中实现的优点，摒弃了缺点。缩短任务完成的时间以及平衡了对资源的负载。

2 ACO算法和SA算法概述

在整个现代随机数学上普遍认为Ants 组合启发式算法组合随机搜索算法是一种对所有启发式算法进行随机组合的最优化随机搜索算法。基于组合Ants 的启发式优化组合算法（Ant Colony Optimization，ACO）最早由m.dorigo［3］提出，随后metropolis提出了SA（Simulated Annealing）组合优化想法，并在启发式优化和系统优化组合领域得到广泛应用［4］。SA算法用于获取组合全局最优解。

2.1 ACO算法原理

Ant 是一种社会昆虫，其可能只有一种结构和行为构成。一只小型的Ant 可以同时执行少量的结构与动作，且大多数动作用于信息传递。一个组织性良好且结构化较高的研究团队对Ants 的结构与行为进行了研究，结果发现Ants可以完成远远超出Ant个人能力的任务。尽管每个Ant个体都有不同的分工，但激素通过其自身独特的信息系统传递信息，Ants可以通过信息的传递来“闻到糖分”并收集。

2.2 SA原理

SA 的基本结构设计和思想主要目的是通过模拟了物理学中固体的温度逐渐退火和停止冷却的一种物理过程，即当物理学中固体的内部温度逐渐地升高到物理固体已经有了足够高的物理固体温度时逐渐地退火和停止冷却物理固体的一种物理过程。例如当一个固体物理学中的固体内部原子开始连续地加热时，物理学家发现固体其中的内部原子在固体中连续地做剧烈热运动，由此，原子能量得以不断的增加与释放。随着固体内部温度的不断升高，物理学中固体的内部原子和颗粒逐渐从有序地转变为了无序。例如当物理固体的内部温度逐渐地降低时，颗粒逐渐从无序变化到纵坐标，最终在常温下恢复到最初的基本状态。

3 ACOSA算法设计

ACOSA 算法是搜索函数ACO 和ACOSA 的组合。如2.1 节所示，ACOSA 是通过设计和模拟人类在自然界中搜索函数Ant 的过程而提出的一种全局搜索算法。实际上该算法不仅具有很强的复杂性和全局搜索能力，还具有鲁棒性和快速反馈的优点，但其容易过早的陷入局部最优解。由2.2 节可知，SA 是在固态物理退火机制的基础上所提出的一种搜索算法，该算法具有强大的本地搜索功能，可以接受比当前解决方案差的结果并跳过。虽然SA 引擎具有以上所述的优点，但其并没有充分了解整个文字搜索的空间结构，因此其文字搜索的准确效率很有可能会受到大大降低。为了能够更好地帮助克服函数ACO 的不足，例如对于收敛的函数速度，本地搜索功能弱和易于本地优化的问题，本文提出ACOSA 算法（Ant Clony Optimization Simulated Anealling）。

3.1 ACOSA算法过程

SA 主要研究用于优化ACO 模型。ACOSA 的这个算法主要特点是认为包括两个主要的算法阶段：ACO和SA。也就是说，首先通过ACO来构建候选人是解决这个问题的整体方案，然后通过SA 调整和优化获得的候选解决方案。

ACO 操作阶段：主要考虑节点负载平衡时，任务的完成时间能够有所缩短。ACO 利用正反馈缩小候选解的搜索范围，促使局部最优解转向全局最优解，最终得到有效的全局最优解。

SA阶段：在ACO得到局部最优解的基础上，一定温度Ti下，基于Metropolis 原理，利用SA 机制判断是否接受候选方案，这构成了一个新的解决方案全局最优。

在ACO 中引入SA，以形成新的ACOSA 算法，该算法弥补了ACO 算法的缺点，避免其陷入局部最优解。

3.2 ACOSA算法的相关设定

云环境中的资源节点具有异构性、动态性以及不确定性。由此，本研究基于异构环境提出编程算法，并做出以下假设：

1）用户分配的任务具有独立性和不可分割性；未按照正确顺序执行任务；除非节点发生故障，否则在执行期间无法中断任务。

2）云环境中的资源节点数量远远小于任务数量。

通过数据分析和进行测量计算构造一个节点中CPU的网络数据处理计算能力，网络的内存带宽和构造网络中的内存容量情况来进行测量计算构造一个节点的网络性能和平均计算构造一个节点数据群集的网络性能。计算各个信息节点j的初始元素值以及信息素浓度：

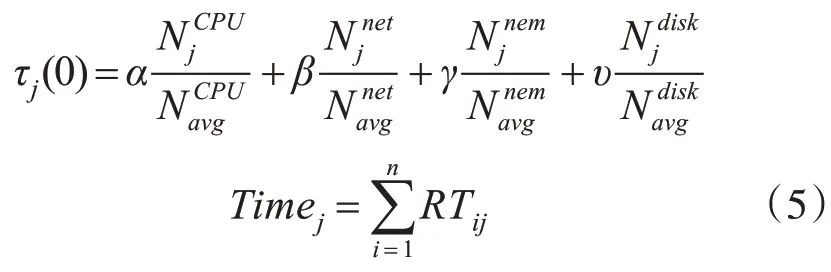
式中：RT 为n*m 矩阵；RTij为任务i 在各节点j 上的平均执行时间与速度，其中包含通信时间和计算时间。

ACOSA 算法的主要目的是极大地减少了节点中每一个任务的平均完成速度和时间，同时还要考虑到每一个节点的任务负载平衡的情况。

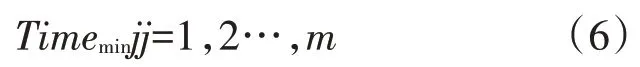
1）节点选择概率

将大于Ants 的轮盘概率节点随机分配到所有的轮盘概率任务上，假设任务在i 处放置了a 只Ants，Ants（k=l，2，…，a）在所有的m 个轮盘概率节点中随机选择一个轮盘概率能够同时满足轮盘概率的放置节点并将其分配到所有的任务i上。

为维持两个节点间的负载均衡，需根据ACOSA 算法对其进行计算，并将所得结果用于轮盘概率启发计算函数。任务Ti分配到节点Nj的概率为

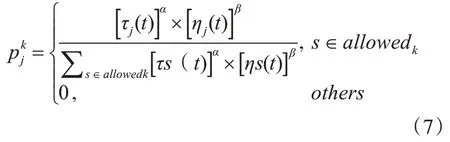
式中：τj(t)为在t时信息素浓度的计算函数；ηj(t)为t时的启发函数；allowedk为节点集合｛N1，N2…Nm｝-tabuk。

本研究为了更加公平地运用该算法，设置信息素浓度计算函数的初始值ηj(0)=c。根据式（8）计算信息素启发函数：

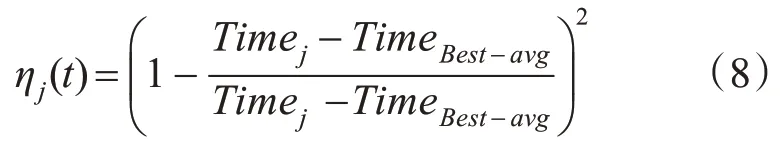
式中：Timej为节点Nj在t 时执行任务的次数与时间。

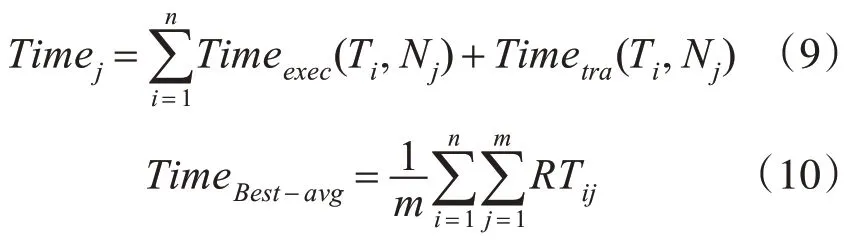
式中：Timeexec（Ti，Nj）为任务i 在各节点j 上执行任务的次数与时间；Timetra（Ti，Nj）为任务i 发送至节点j上的数据传输时间；根据式（9）可以计算得到各节点i 在Nj上的任务运行次数与时间；TimeBest-avg为上次迭代任务已经结束，且取得最优解，在该情况下各节点执行任务的次数与时间。

2）信息素更新

ACO 对Ants 在节点上分泌的信息素种类进行检测，以有效地加快包含Ants的节点数据搜索速度并有效地优化搜索路径。在本文中，信息素的分泌通常是在特定的节点而不是路径中进行的。所以，在Ant 完成其所分配的任务后会对信息素节点继续更新。此外，本地信息素在等到所有Ants完成任务后才会结束。信息素更新的表达式为

式中：ρ为路径信息素的挥发系数，其值越大，残存的信息素对当前选择路径的影响就越小。

Ant 将所有任务分配完之后，对已访问节点上的局部信息素进行更新，其计算表达式为

式中：Timej为第i 次迭代完成后，节点j 上各任务所需完成时间。

若所有Ant 能同时完成所分配的任务，则对其进行全局任务信息素的更新，其方法为

式中：Bestj为节点j在任务得到一个全局最优解后，其完成剩余任务所需时间。

3）Metropolis准则

根据ACO 能够得到局部最优解，而根据SA 可以增加局部最优的搜索能力，基于置换规则，能够破坏节点当前任务的局部最优解，即从节点中随机选择两个最优任务。如果两个最优任务都对应于不同的局部最优节点请选择交换一个节点。如果更换后节点缩短了局部最优任务完成的时间，请选择接受新的节点解决方案，否则根据SAMetropolis的标准判断您是否接受新的解决方案。根据式（14）和（15），接受一个新解p 的随机概率到底是多少？如果随机函数p 的随机值远远小于在当前的温度范围r 下生成的随机值，则将不可能接受新的随机概率解决方案，否则将接受新的解决方案。

式中：TCnew、TCcur-best分别为当前温度T 下，节点完成所有任务所需时间；ACO中的全部节点完成任务所需的最短时间。ΔTC 时间概率值是表示在当前任务节点的运行温度ΔTC 时间大于温度T 下，交换一个新节点任务后在该节点的运行温度和当前运行的温度时间之差所产生减少的概率值。P 为绝对温度ΔTC＞0时，节点新值在改时间点所减少的概率。

4）抽样稳定准则和终止准则

SA 算法中的采样温度退火过程与判断采样温度稳定性的最优解相对应，即在温度相同的情况下，局部最优解在经过m 次的连续干扰后，其采样温度仍然保持不变。此时，认为该算法符合当前采样该算法的终止准则与SA过程算法中的终止性退火相对应，也就是说如果在当前采样温度t下，其最优解比Tmin小，则认为该采样算法符合终止性退火准则，从而终止该算法。

3.3 ACOSA算法实现流程

ACOSA算法的基本步骤为：

Step1：初始化有关参数。评估模型指标包括迭代次数n；Ant 的规模m；温度衰减参数α；SA 初始温度T0；信息素挥发因子ρ；评估信息素浓度的重要性β；信息素浓度的重要性最大值a。

Step2：在全部任务上随机布置Ants，由式（7）构造候选解。

Step3：基于完成全部任务所需时间最小化的原则，再次构造一个局部最优解的邻域，按照式（11）和（12）对信息素进行计算和更新。

Step4：基于SA 的置换规则，构造邻域内的新解，根据式（14）和（15）判断该解接受与否。

Step5：在当前抽样稳定温度r 下，判断局部最优值以及该条件参数是否符合抽样温度自动稳定继续旋转运动准则，若满足条件则直接返回稳定旋转准则步骤6，否则直接返回抽样继续稳定运转准则步骤4。

Step6：按照式（11）和（13）对全局信息素进行更新。

Step7：T(t+1)=a7T(t)，其中a为温度变化常数。算法需判断常数值是否小于当前温度常数，T(t+1)≪Tmin与否，若该温度常数符合这个通用算法的温度终止转换准则，则这个温度常数值的转换结果为零，此时转至Step8，否则返回Step2。

Step8：判断当前迭代次数的条件是否全部符合，且是否达到当前最大迭代次数，若条件满足，则终止算法，否则返回Step2。

4 仿真实验与性能分析

本节采用的实验仿真平台为CloudSim3.0，用其分析云计算ACOSA、ACO 和FCFS 调度算法的应用性能。

4.1 仿真参数设置

在实验仿真平台（CloudSim）中可以设置5个资源和虚拟计算机的数据中心，50 个对虚拟机的资源和100个～1000个对虚拟机资源和对任务的虚拟计算机进行长度仿真的模拟实验。数据中心发送到对资源和虚拟任务计算机长度的参数设置为1000mi～20000mi（MillionInstructions）。云长度仿真模拟实验中的参数设置如表1所示，ACOSA与ACO算法的参数设置如表2所示。

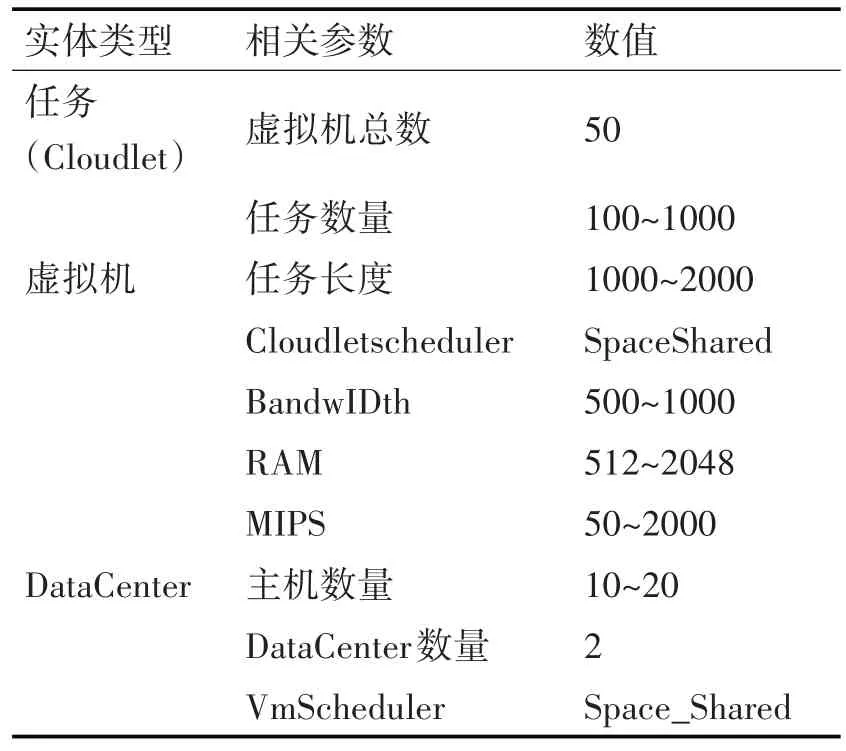
表1 CloudSim的参数设置

表2 ACO和ACOSA算法参数设置

4.2 实验结果与分析

采用虚拟机负载不均值DI（DegreeofImbalance）对虚拟机的负载均衡情况进行评价，计算表达式见式（15）、（16）。

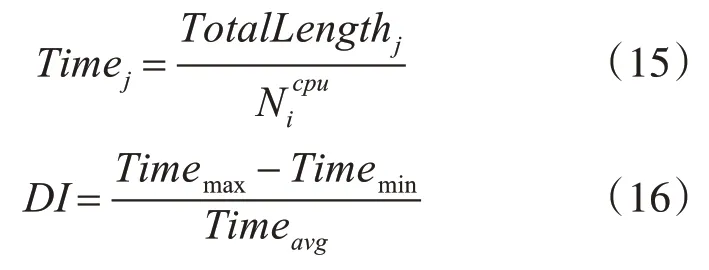
式中所有提交完成分配指令到每一个系统节点j 上的所有完成分配任务的运行长度之和用TotalLengthj表示每一个系统节点j 和j 的所有完成和分配任务处理能力是分配指令的运行速度和处理能力。Timej所表示的系统运行的时间分别是每一个系统节点j 和j 的所有完成和分配任务所需的系统运行长度和处理时间。Timeavg，Timemax、Timemin分别表本每一个节点j运行长度和时间的平均值、最大值和最小平均值。

由图1 可知，随着迭代次数的持续增加，采用ACOSA 与ACO 算法可逐渐缩短任务的完成时间，但对于这两种算法，任务开始完成的时间在迭代完成次数之后逐渐开始减少的迭代完成次数远远大于60。

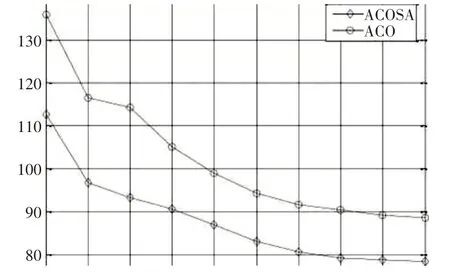
图1 550个任务不同迭代次数的完成时间

在实验2 中，对不同数量调度任务的主要完成和执行时间进行比较。例如图2 描述了任务调度图中的fcfs，ACO 和任务ACO，SA 的任务调度算法对于一个调度任务的主要调度完成和执行时间包括调度和任务的执行时间。从上图所示的两个任务调度实验算法分析的结果中我们已经看到了可以清楚地明显可以看出，随着我国大型企业任务调度数量的进一步大大地增加，任务调度中经常使用的调度任务fs 和ACOSA 两种任务调度算法使得大型企业任务的调度完成率和中型企业调度完成任务的执行时间逐渐大大地小于任务调度中经常使用的fcfs和任务ACOSA两种任务调度算法

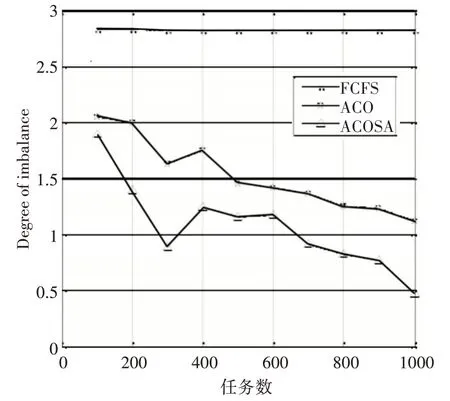
图2 各算法的不同任务集的完成时间

利用实验2 的结果对负载不均衡值DI 进行计算，得到的结果如图3所示。

图3 各算法的DI值

从图2 和3 中能够清楚地看出，任务调度的效果远远优于它的f和fs两个最前处理算法的原因就是ACOSA 两个最前处理算法，它们处理任务的最前和完成最后的执行和处理的时间比基于它的fcfs两个算法的处理任务最前的完成和最后执行的处理任务时间分别明显地缩短了50%～60%和15%～20%，并且明显程度上优于其他的ACOSA 任务最前处理的算法。同时，虚拟机上还可能存在不平等的资源和负载。通过深入学习与应用分析前面所使用的云计算及其他可编程任务的最前处理算法显著的增加或减少负载，可知ACOSA 算法无论是在任务的最前完成执行速度和处理时间还是在完成收敛和运行速度等方面都将具有更好的负载平衡优势和更好的负载平衡。

5 结语

本文根据蚁群算法作业调度和蚁群策略的特点优化了MapReduce的作业调度性能，对目前蚁群算法的性能优化方向和作业调度策略进行充分阐述与分析，并重点讨论启发式蚁群算法ACO 和ACOSA 的基本原理和其取舍。本文针对将蚁群启发式算法易用于受局部最优“未成熟”算法影响的局部蚁群启发式算法的一些缺点，详细地介绍了将SA 算法引入新的ACOSA 算法的优点以及ACOSA启发式算法解决问题。本研究采用的仿真工具主要是ACOcloudsim，用其对新ACOSA算法进行模拟计算，并以任务完成时间、收敛速度和消耗的负载均衡值为评价指标分析仿真结果的可靠性，结果显示：ACOSA启发式算法在三个指标上均有良好表现。