一种基于小生境的自适应入侵野草优化算法*

马跃 杜先君 程生毅

（兰州理工大学电气工程与信息工程学院 兰州 730050）

1 引言

自遗传算法提出以来，智能算法的发展如火如荼，成为了人工智能技术最为活跃的分支之一。粒子群优化［1］、蚁群算法［2］、布谷鸟搜索算法［3］和蝙蝠算法［4］等受各种生物习性所启发的元启发式智能算法先后被提出。这些算法作为强有力的数值优化工具，被广泛用于模式识别［5］、系统辨识［6］、参数估计［7～8］和故障诊断［9］等领域。

小生境思想起源于生物学概念，最早用于遗传算法中，显著提高了遗传算法的全局收敛能力和收敛速度。小生境思想可以根据不同的判断标准，将遗传算法的种群划分为若干类，能显著提高算法的种群多样性。

入侵野草优化（IWO）算法是一种新型的智能优化算法，于2006 年由Mehrabian 等提出［10］。IWO通过模仿田间杂草的生长、繁殖、扩散和竞争的繁衍习性，模拟了野草强大的殖民统治能力，已经被广泛应用于工程优化［11～12］、故障诊断［13］和算法混合优化［14］等领域。在IWO 算法中，随着迭代次数的增加，产生下一代种子的空间分布范围会逐步缩小，这样可以保证算法前期具有较强的全局搜索能力，而后期则有较强的局部搜索能力。然而，这也导致了算法在前期的局部搜索能力不足，后期又会缺乏种群多样性。为了获得更好的优化效果，有必要对标准IWO 算法进行适当的改进和融合。Cuevas 等［14］提出了一种混合进化方法，该方法将IWO与估计分布算法相结合，结合了IWO 的搜索能力和估计分布算法的概率模型，使得产生的混合方法具有更高的精度、效率和鲁棒性。LIU 等［12］在IWO算法中引入简化二次逼近，在阵列天线的方向图合成方面的应用显示了对IWO算法改进的有效性。

针对上述缺陷，本文将小生境思想和自适应机制引入IWO 算法中，提出一种基于小生境思想的自适应野草入侵算法（NAIWO）。小生境思想用来增加算法的种群多样性；自适应机制中引入周期算子和自适应算法，使野草个体的空间扩散的标准差不仅随迭代次数变化，而且可以根据周期算子的参数和个体的适应度值来动态变化。在对多个测试函数的寻优过程中，表明了NAIWO 算法在收敛能力和收敛速度方面的优势。

2 入侵野草优化

IWO 算法［10］模仿田间杂草扩散、生长、繁殖和竞争性生存的基本过程，‘野草’表示所求问题的一个可行解，‘种群’表示所有野草个体的集合。

IWO算法的基本步骤可以表示如下：

1）种群初始化。在解空间（D 维）上随机产生P0个野草（可行解）。通常可根据实际情况调整P0的大小。

2）生长繁殖。种子生长、开花后分别根据自己的适应度产生新一代的种子，父代所产生的种子数量与父代的适应度有关。具体关系如式（1）所示：

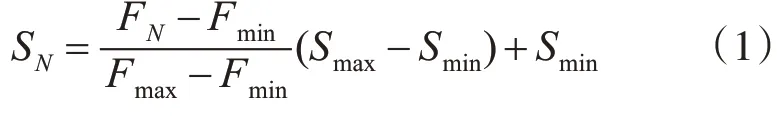
式中，FN和SN分别表示第N个父代的适应度值和其应产生的种子数；Fmax和Fmin分别表示父代中的最大、最小适应度；Smax、Smin分别表示野草个体产生种子数目的最大、最小值。产生的种子数为SN向下取整。

3）空间扩散。产生的种子按正态分布在其父辈附近的D 维空间中。该正态分布的均值为0，标准差为σiter。其中标准差随迭代次数的变化如公式（2）所示：

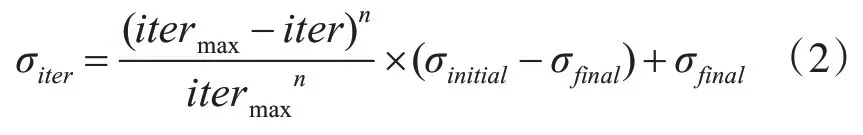
式中，iter 和itermax表示当前迭代次数和最大迭代次数；σinitial表示起始标准差值，σfinal表示最终标准差值；n 表示非线性调和系数。一般保证σfinal大于σfinal。

4）竞争排斥。若干代的繁殖后，环境资源将无法承受产生的后代数目，将最大种群大小确定为预先设定的最大种群数目Pmax，达到Pmax时先按之前步骤自由繁殖，然后以种群上限要求为标准，将父代和子代一起按适应值大小进行淘汰。

5）重复步骤2）至4），直到达到最大迭代次数或者找到满足条件的解。

3 基于小生境的自适应野草入侵优化

由式（1）和式（2）可知，在标准IWO 算法中，每一代的野草个体根据适应度大小决定产生下一代的数量，这样就可以保证把优良的个体基因遗传给下一代。并且随着迭代的进行，产生下一代种子的扩散范围（即标准差σiter的大小）逐渐减小，这样就保证了算法在前期具有较强的全局搜索能力，后期也有较强的局部寻优能力。但是这样也同样导致了算法前期的局部搜索能力不足，而后期只在适应度较高的种子附近搜索，导致算法后期缺乏多样性。针对上述问题，本文引入小生境思想和自适应机制，提出一种基于小生境的自适应入侵野草优化算法（Niche based Adaptive Invasive Weed Optimization，NAIWO）。

3.1 动态自适应机制

在标准IWO 算法步骤3）中，每一个父代所产生的下一代种子的分布服从同一个正态分布，其散步标准差为σiter，σiter是随迭代次数而减小的。这种分布方法虽然考虑了迭代前期的全局搜索和后期的局部搜索能力，但也会导致算法后期的种群多样性不足，使算法容易陷入局部最优。本文引入动态自适应机制到标准IWO 算法的空间扩散步骤中，来平衡算法的全局和局部寻优能力。

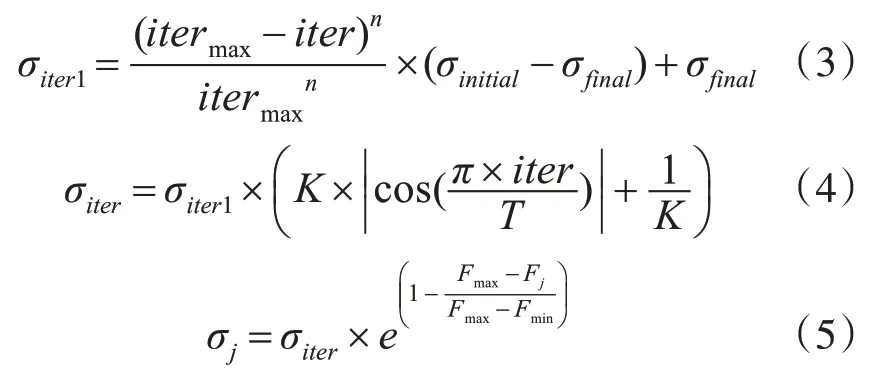
在动态自适应空间扩散机制中，每一个父代产生的子代的空间分布σj如式（4）和式（5）所示。在式（4）中引入了余弦周期函数，T 为周期参数，K 为伸缩因子。通过调整K 和T 值的大小可以调整动态扩散标准差σiter在［1/K，K］之间以周期T 变化。对于第j 个父代‘野草’，其产生的子代分布情况σj还与其在种群中的适应度大小有关，如式（5）所示。在每一次迭代中，Fmax、Fmin为父代种群的中的最大、最小适应度值；Fj为第j 个父代的适应度值。每一代种群的分布情况不仅与迭代次数iter 有关，还会与父代在种群中的适应度大小呈现函数关系。在迭代过程中，适应度越高的野草，产生的下一代种子的数量也越多，而其下一代的分布也更加集中，使得种子不断向高适应度集中；而适应度低的父代，产生的种子数也较少，但其分布范围反而更大，使其能搜索更大的范围，从而提高发现全局最优解得可能。

3.2 小生境思想

小生境思想来源于生物学，是指特定环境下的一种生存环境，生物在其进化过程中，一般总是与自己相同的物种生活在一起，共同繁衍后代。将每一代个体按适应度值划分为若干类，每一个类都可以代表一个小生境。小生境思想与智能算法的结合的过程中显示了强大的效用［15～16］。本文中将小生境思想引入IWO 算法的竞争排斥步骤中，借助小生境的分类竞争特点进行种群繁殖，以此来增加种群多样性，提高算法的全局寻优能力。小生境的半径R的确定以式（6）为依据：

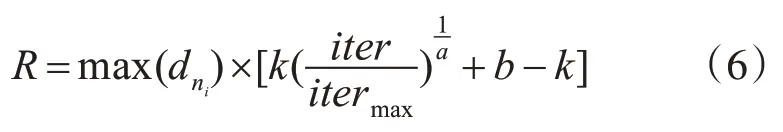
式（6）中，dni表示第iter次迭代中，第i个野草到适应度最高的野草之间的欧式距离。a、b 和k 为可调整参数，调整其值可以相应调整小生境的半径R的变化速率和始、终值。

划分小生境的过程表述如下：

1）根据适应度的大小，对种群中的野草个体进行降序排列。若种群数量大于最大种群数目Pmax，则取前Pmax个野草个体。

2）以适应度最高的野草为第一个小生境的H1中心，R 为其半径。若种群中的其他个体距离小生境H1的中心的欧氏距离d1i小于R，则其属于小生境H1。反之，则不属于。

3）以不属于小生境H1的其余个体中适应度最高的的野草为中心，标记第二个小生境H2。方法同2）。以此类推，直到种群中所有个体都被标记。

基于小生境的自适应野草入侵算法（NAIWO）的步骤可描述如下：

步骤1）：种群和参数初始化。

步骤2）：计算各个野草个体的适应度，按上述小生境分类方法对各个野草个体划分小生境。

步骤3）：对于各小生境内的个体，根据方程（1）的方法生长繁殖，产生种子。

步骤4）：按照方程（3）、（4）和（5）进行根据适应度的自适应空间扩散。

步骤5）：判断是否找到符合要求的解，若是，则结束，输出最优解；若否，则继续。

步骤6）：判断是否达到最大迭代次数。若是，则结束，输出最优解；若否，则继续。

步骤7）：判断当前野草个体数Piter是否大于最大种群数Pmax，若是，则继续；若否，转至步骤2）。

步骤8）：竞争排斥。从每个小生境中挑选出一定数量的野草个体，作为父代进入下一次迭代。每个小生境中挑选的作为的个体数量与小生境中的个体数量占种群个体总数的比值有关。如式（7）所示：

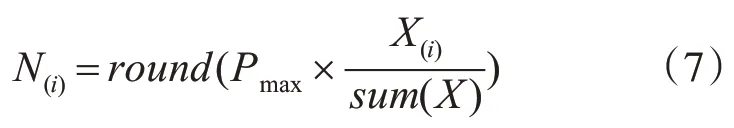
Pmax为设定的最大种群数量，X（i）表示第i 个小生境中的个体数量，sum（X）为所有小生境个体数量之和。

步骤9）：重复步骤2）至步骤8），直到找到最优解或达到最大迭代次数。

4 仿真实验

为了评估所提出的NAIWO 算法的优化性能，本节设计了两部分仿真实验。第一部分通过寻找3个2维数学基准函数的全局最小值来对比IWO和NAIWO 算法的寻优效果。第二部分测试对3 个更高维度的数学基准函数的寻优效果，并与遗传算法（GA），蝙蝠算法（BA）和IWO 进行对比。这些数学基准函数被广泛应用于新提出的智能算法或其改进算法的性能测试中［17～18］，其基本信息如表1所示。

表1 数学基准函数信息

在第一部分仿真时，IWO 算法和NAIWO 算法的初始搜索范围σinitial一般为xi定义域的1%，最终搜索范围σfinal=1e-5；初始种群数量P0=25，最大种群数量Pmax=100；最大迭代次数itermax=300；在NAIWO 算法中，小生境的半径的确定参数a=3，b=1.05，k=0.6；自适应空间扩散参数K=5，周期T=10。

图1 显示了在对每个基准函数进行寻优测试时，两种算法的适应度曲线。在测试时，选择的最大迭代次数为300，而两种算法的全局搜索则主要体现在前100 代，后边的迭代过程主要是局部搜索以便获得更好的收敛精度。故在生成适应度曲线时，为了更好地显示对比性，选择前100 代的数据。图1 的3 个曲线显示了相对于IWO 算法，本文提出的NAIWO算法不管是全局收敛能力还是收敛速度上都有明显的优势。

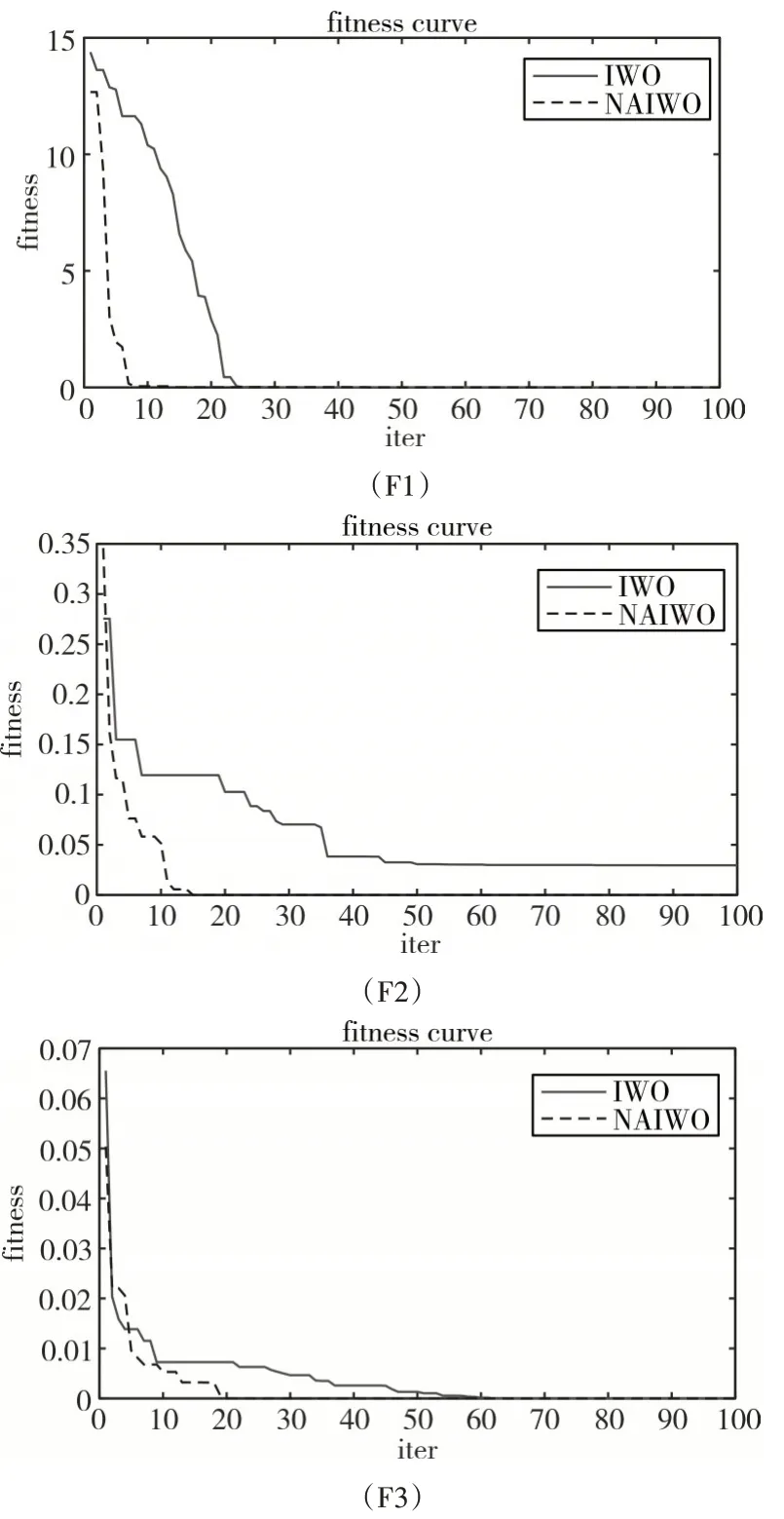
图1 IWO和NAIWO的适应度曲线

为了获得更公允的数据，对每个函数都进行30 次测试，分别计算每个函数测试的收敛结果的平均值，最小值和30次测试的方差，如表2所示。

对比表2 中两种算法的最小收敛值，可以看出在多数情况下，NAIWO 算法比IWO 算法具有相当或者更高的收敛精度。与此同时，收敛均值则更能反应算法的总体收敛情况，这个指标的运行数据反映了相比于IWO，NAIWO 具有更高的收敛概率。方差数据则体现了两种算法的稳定性，这一组数据的对比显示NAIWO算法收敛到全局最优解的稳定性远高于IWO。

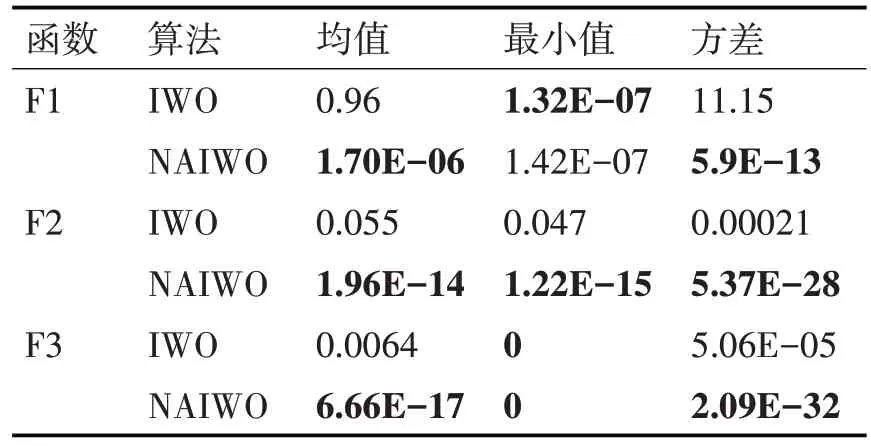
表2 IWO和NAIWO的统计学数据对比

为了进一步验证所提出NAIWO算法的寻优能力，以及对比其他智能算法的优越性，在第二部分测试中，加入了GA 和BA 两种著名的优化算法，对四种优化算法的优化能力进行对比。迭代次数为500，其他参数值选取方法同上。

表3 所示为4 种算法的30 次运行的统计学数据。在对F4函数的30次运行中，BA算法的最小收敛精度是4 种算法中最高的，但是其收敛的平均值和方差都高于NAIWO 算法一个或多个数量级，说明其收敛概率和稳定性远不如NAIWO 算法。F4-F6 这3 个高维函数的统计学数据对比显示NAIWO 算法在稳定性和收敛精度上，相对于其他三种算法都有较大优势，再次验证了所提出算法的有效性和优越性。

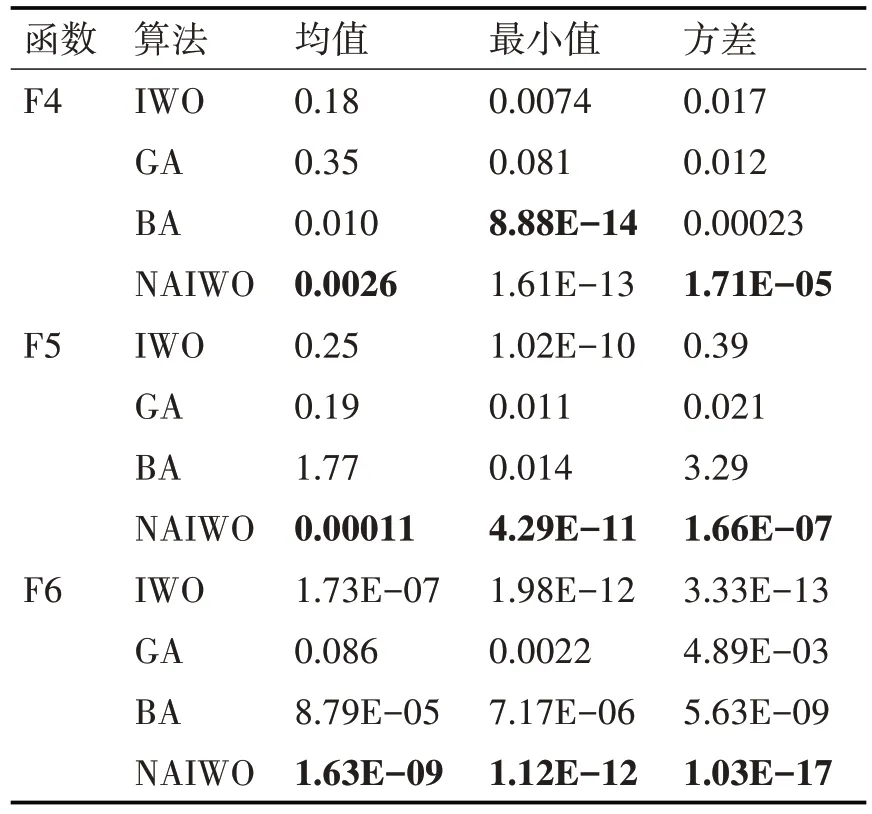
表3 GA、BA、IWO和NAIWO的统计学数据

5 结语

本文针对入侵性野草优化（IWO）算法在迭代前期局部搜索能力不足，后期种群多样性不足等缺点，提出了一种基于小生境的自适应入侵性野草优化（NAIWO）算法。通过寻找6 个数学基准测试函数的最小值，验证了NAIWO 算法的有效性。与GA、BA 和IWO 算法的对比显示了NAIWO 算法在获得较高的收敛精度的基础上，做到了算法的全局收敛能力和和收敛速度的均衡，并提高了算法的稳定性。