基于Watterson 信道模型的短波信道仿真与实现*

王健 孙 洁

（1.武汉邮电科学研究院 武汉 430074）（2.烽火通信科技股份有限公司 武汉 430205）

1 引言

目前，新型无线电通信系统不断出现，短波这一古老、传统的通信方式仍然受到全世界的普遍重视，不仅没有被淘汰，而且还在不断地快速发展。因为它有着其他通信系统不具备的优点［1］。评估短波通信系统的性能通常有两种方法，即理论分析和实验测量［2］。在理论分析方法中，目前比较常用的有以下几种短波信道模型：1）Watterson 等提出的高斯散射抽头延迟线模型［3］；2）Hoffmeyerd 等提出的基于电离层参数的信道模型［4］；3）Giles等提出的基于短波信道冲激响应的直接测量法模型［5］；4）V.E.Gherm等提出的基于散射函数的宽带短波信道模型［6］等。而Watterson 模型因其复杂度低且能较好地反映短波信道的传输特点，在这几种模型中被广泛应用并被CCIR推荐［7］。

2 Watterson信道模型

短波信道在时间和频率上都是不稳定的，但是如果将信道带宽限制在10kHz以内，信号的传输时间足够短（小于10min），那么大多数信道是相对稳定的［3］。从1965 年开始，经过5 年时间的研究，Watterson 等提出了一种高斯散射抽头增益延迟线模型来模拟短波信道，简称Watterson 信道模型［3］。该模型如图1所示。

图1 Watterson信道模型

图中i是整数，表示第i条抽头或路径，τi表示第i条路径的时延，n是路径的总数，随机过程Gi(t)是第i条路径的抽头增益函数。输入信号首先被送入抽头延时器，每个抽头可以看作是电离层的一条传播路径，通过改变时延τi的值来模拟多径效应。然后，不同的Gi(t)对延时后的信号的幅度和相位进行调制来模拟多普勒频移与多普勒频率扩展。最后延时和调制后的各路信号相加，再加上噪声和干扰形成输出信号。

2.1 Watterson信道模型的假设条件

关于抽头增益函数Gi(t)的统计性说明包含三个假设条件［3］。

1）瑞利衰落假设：假设每一个抽头增益函数Gi(t)是一个复高斯随机过程，其幅度服从瑞利分布。根据瑞利分布的概率密度函数，可得到抽头增益函数Gi(t)的概率密度函数为

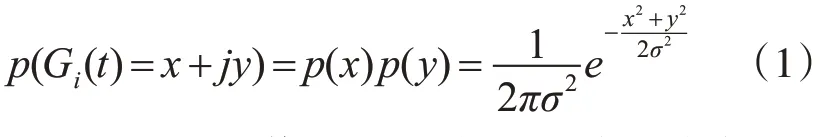
这里，Gi(t)的均值为0，幅度服从瑞利分布，相位服从均匀分布。

2）独立性假设：每个抽头增益函数Gi(t)都是相互独立的。因此，任意两条路径抽头增益的联合概率密度函数就可以表示为

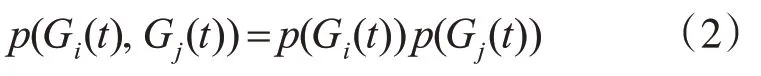
3）高斯功率谱假设：假设抽头增益函数Gi(t)的功率谱v(f)具有高斯分布的形状或者可以看成是两个具有高斯分布形状的频率函数的和［5］：

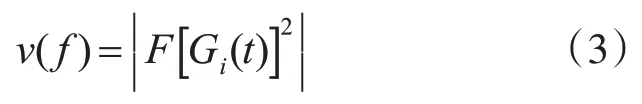
这里F[].表示关于t的傅里叶变换。

这里fa和fb为分量a和b的多普勒频移，σa和σb为分量a和b的多普勒频率扩展的因子，Ca和Cb为分量a和b的功率增益。

2.2 Watterson信道模型的传输函数

Watterson信道模型的时变频率响应可表示为

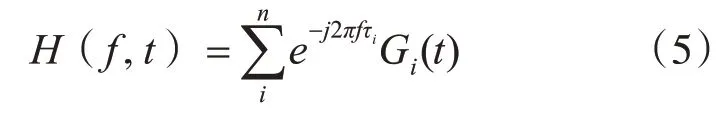
抽头增益函数Gi(t)反映了高频信道的时变衰落特性，可以表示为

式中Gia(t)和Gib(t)是两个相互独立，各态历经的复高斯平稳随机过程，它们是相互独立的正交分量，均值为0，有相等的均方根值和频谱。

将Gia(t)定义为实部和虚部的形式：

(0)是Gia(t)的自相关函数在Δt=0 时的值，代表信道输出信号功率与输入信号的比值，即功率增益。Gi(t)的自相关函数［8］为

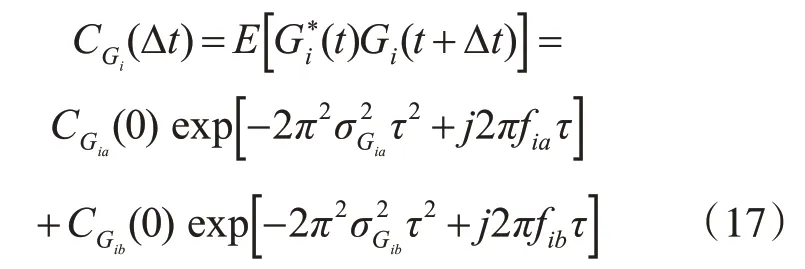
根据维纳-辛钦定理，可以求得Gi(t)的功率谱密度［8］为

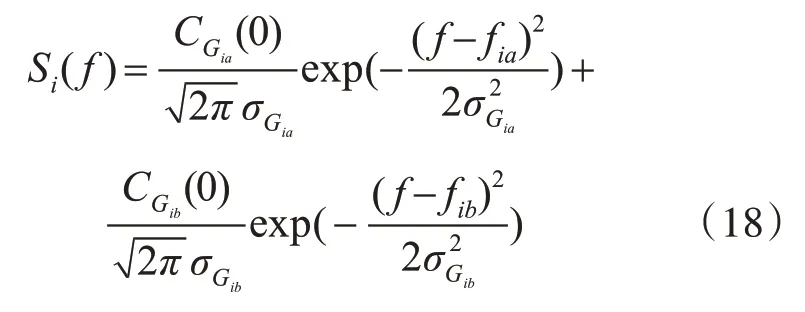
这里Ci(0)=Cia(0)+Cib(0)，fia和fib为多普勒频移的值，2σGia和2σGib为多普勒频率扩展的值。

3 Watterson信道模型的仿真方法

根据以上对Watterson 信道模型的分析，可以设计出如图2所示的结构框图［9］来进行仿真。

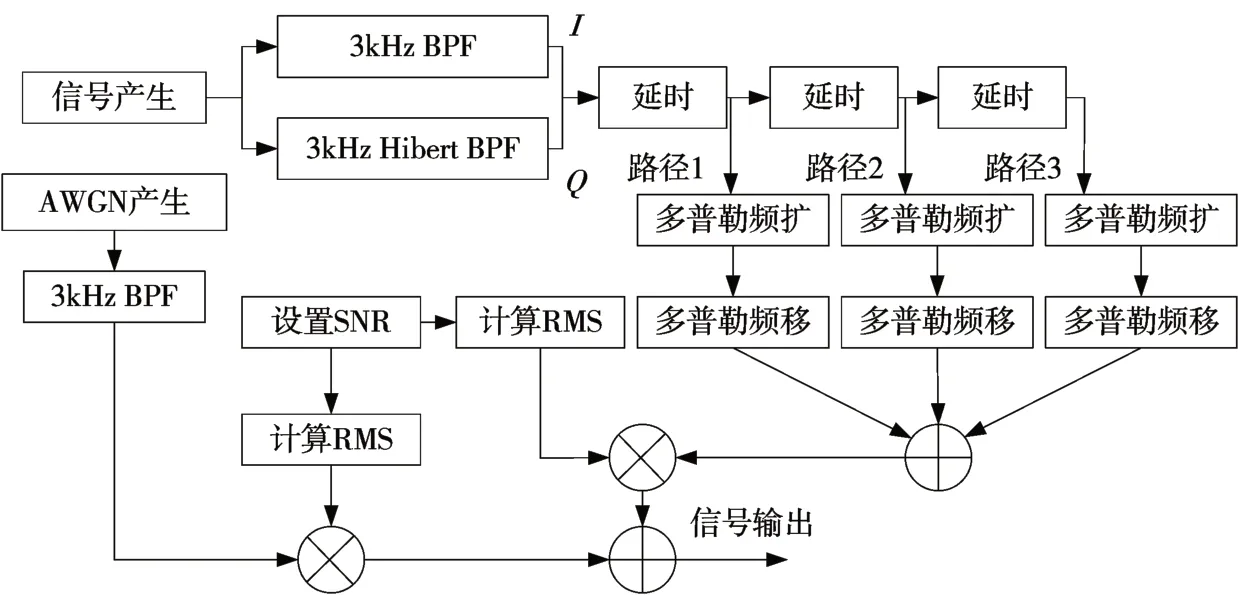
图2 Watterson信道模型的结构框图

Watterson 信道模型的仿真主要分为希尔伯特（Hilbert）滤波器的仿真、多径效应的仿真、多普勒频移的仿真、多普勒频率扩展仿真和噪声仿真五部分。以下对每种仿真进行说明。

3.1 希尔伯特（Hilbert）滤波器的仿真方法

首先产生一个输入信号，将该信号一路输入3kHz的带通滤波器（BPF），另一路经过希尔伯特变换后再输入3kHz 的带通滤波器，这样就形成初始复信号I+jQ。经希尔伯特变换后，I、Q 两路信号的幅度不变，相位相差90°。具体的实现方法［10］如下。

1）设计一个通带带宽为1500Hz的有限冲击响应（FIR）低通滤波器（LPF），其通带带宽是带通滤波器的一半。

2）通过转换式（19）和式（20），将低通滤波器的系数变为带通滤波器的系数：

式中，hIBP(n)和hQBP(n)是希尔伯特带通滤波器的系数，hLP(n)为n 阶有限冲击响应低通滤波器的系数，f0为滤波器通带的中心频率，T 为采样周期，N为希尔伯特滤波器的阶数。

3.2 多径效应的仿真方法

设经过3kHz 带通滤波器和3kHz Hilbert 带通滤波器之后的信号为S（t），则S(t)=Iin(t)+jQin(t)，Iin(t)=acos(2πf0t+θ)，Qin(t)=asin(2πf0t+θ) 。模拟多径效应，只需每一路径设置不同τi的值，这样每路就产生了不同的时延，由此得到：

3.3 多普勒频率扩展的仿真方法

多普勒频率扩展具体的结构框图［11］如图3 所示。

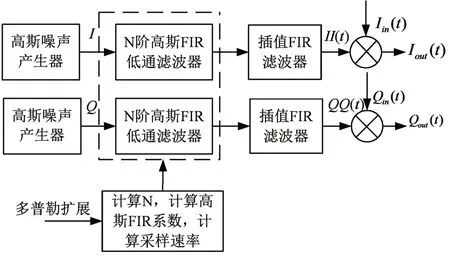
图3 多普勒频率扩展的仿真结构框图

设多普勒频率扩展前的输入信号为S(t)=Iin(t)+jQin(t)，通过插值滤波器后的信号为N(t)=II(t)+jQQ(t)，将两个复序列相乘得到：

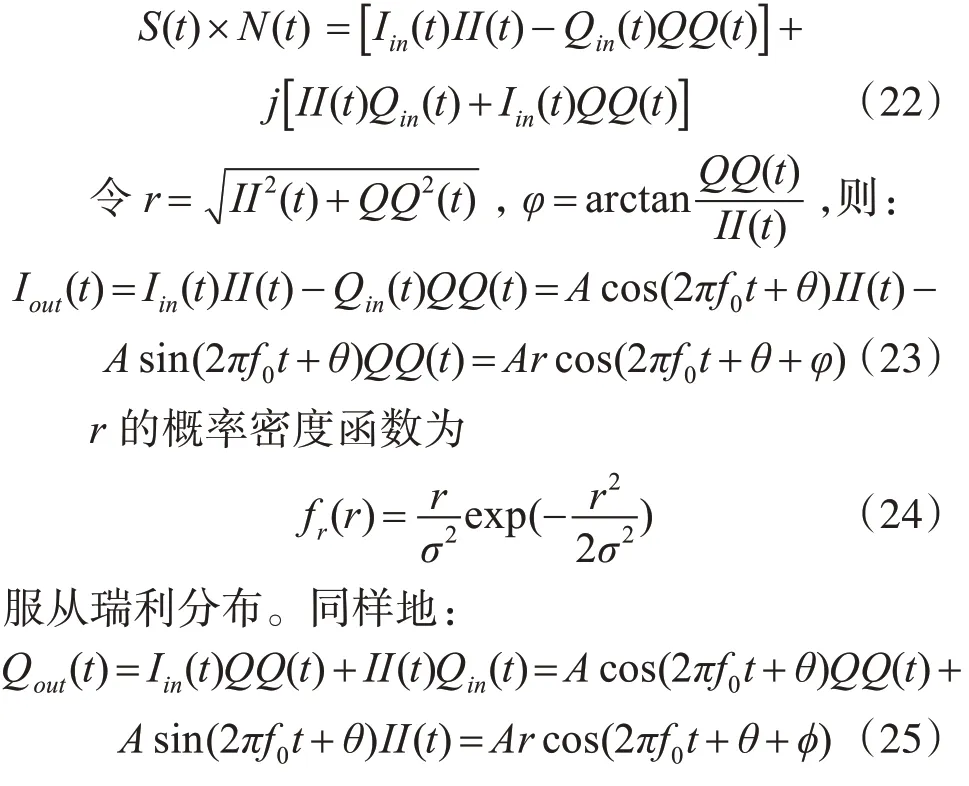
3.4 多普勒频移的仿真方法

多普勒频移仿真框图［12］如图4所示。

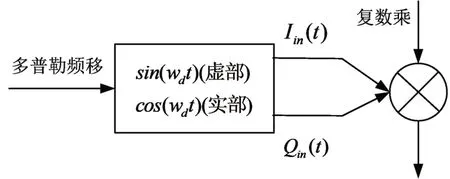
图4 多普勒频移的仿真结构框图

设多普勒频移为fd，I(t)=cos 2πfdt，Q(t)=sin 2πfdt，多普勒频率扩展后的信号为S(t)=Iin(t)+jQin(t)，多普勒频移后的信号为Sfd(t)=Ifd(t)+jQfd(t)。

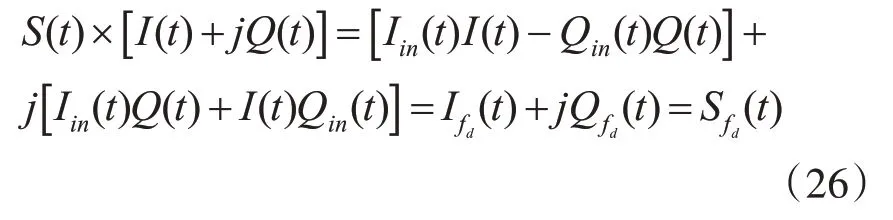
这样就实现了多普勒频移，这时，信号的频率变为f0与fd的和。

3.5 噪声的仿真方法

信号或者噪声的均方根可以由式（27）计算［13］：

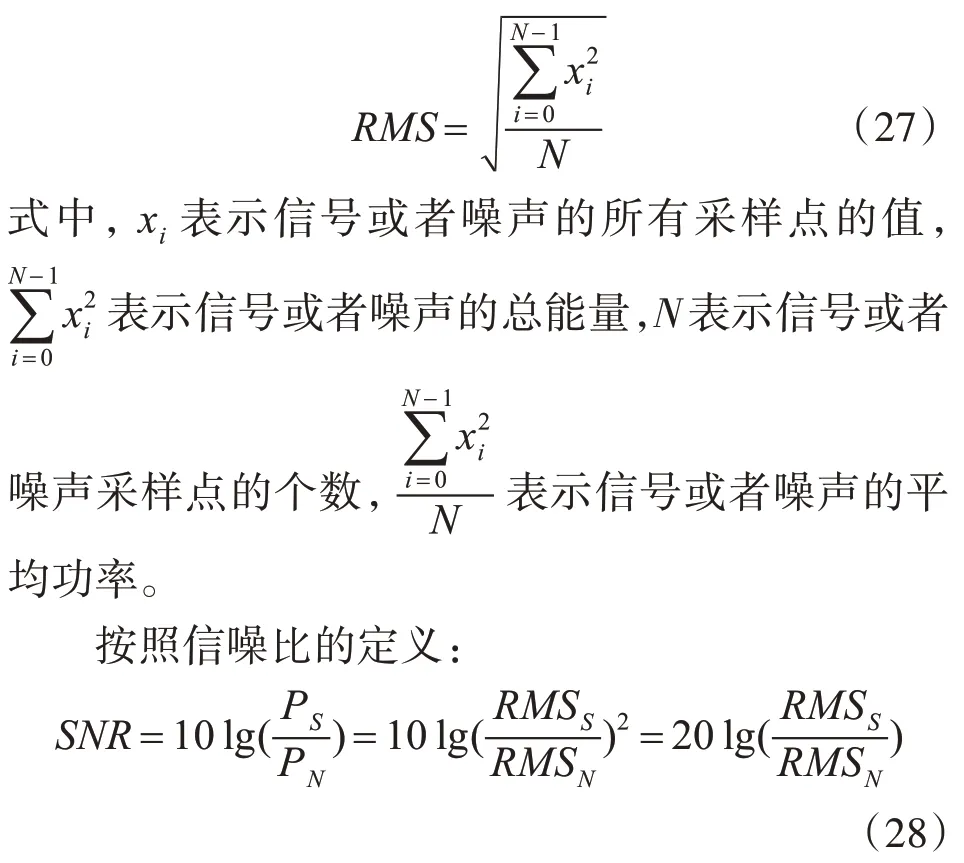
式中，RMSS表示信号的均方根值，RMSN表示噪声的均方根值。当信噪比确定后，只需改变RMSN的值，从而达到增加或者减小噪声的目的。

4 仿真结果

实验采用CCIR推荐的中纬度地区干扰环境下的短波信道参数［14］，时延为2ms，多普勒频扩为1Hz，不涉及多普勒频移的考虑。输入信号选择单频信号x(t)=cos(2πf0t)，f0=400Hz，抽样频率fs=3000Hz，信噪比为20dB。输出信号如图5所示。

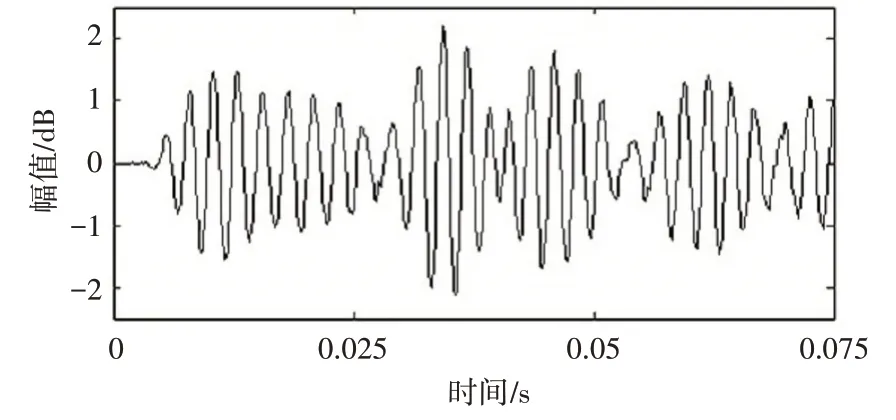
图5 输入为单频信号时的输出信号时域图

从输出信号的时域图可以看出，信道对输入信号的相位和幅度产生了随机性的调制，输出信号衰落明显。输出信号的频谱图如图6所示。

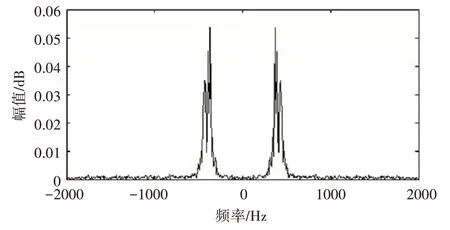
图6 输入为单频信号时的输出信号频谱图

可以看出，输出信号的频谱不是δ函数的形式，出现了两个谱峰并有一定的宽度。这表明输出信号的频谱出现了偏移和展宽，产生了多普勒频移和多普勒频率扩展的现象，并叠加了白噪声的频谱。

在上述基础上将多普勒频扩设定为2Hz，输出信号的时域图和频谱图分别如图7和图8所示。

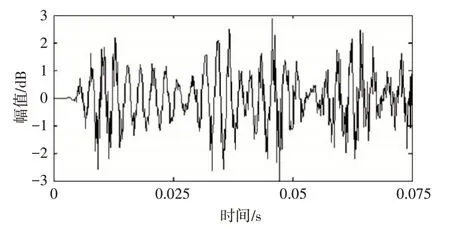
图7 增加频扩后的输出信号时域图

图8 增加频扩后的输出信号频谱图

可以看出输出信号的衰落和频谱展宽更大，同时噪声对输出信号的影响也更为明显，清楚地显示了频率扩展增加带来的影响。

5 结语

本文对Watterson 短波信道模型进行了理论推导，并在此基础上对模型的仿真方法进行了详细分析。通过Matlab编程，将单频信号作为输入信号通过Watterson 信道模型，给出仿真结果，并对结果进行了分析。结果表明，仿真验证了Watterson 短波信道模型算法的正确性和可行性，该模型可以很好地模拟短波通信信道中存在的多径延迟、多普勒频移和多普勒频率扩展等现象，这对短波通信系统和设备的前期设计具有重要意义。