基于最小二乘法-加权马尔科夫链模型的母线负荷预测*

杜雅楠 齐敬先 施建华

（南瑞集团有限公司（国网电力科学研究院有限公司）南京 211106）

1 引言

母线负荷是变电站的主变压器其供电区域的终端负荷的总和［1～3］。母线负荷是系统负荷的细化，其以节点负荷为预测对象，其预测结果用于电网安全校核，为动态状态估计、安全稳定分析、无功优化、厂站布局控制等提供良好基础。相较于系统负荷预测，母线负荷预测由于其供电范围小，受供电区域内用户和小电源影响较为明显，故而母线负荷易突变、稳定性较差。季节影响导致母线负荷数据存在高频波动分量和季节分量，多种信号较差对其预测样本数据的质量产生较大影响［4］。同时，由于数据采集传输造成的错误数据和运行方式变化易导致数据突变，数据质量下降。对母线负荷数据的预处理包括经验修正法、曲线置换法、插值法及小波分析等［5～9］。

母线负荷预测方法主要包括基于系统负荷分配预测法及基于节点负荷自身变化规律预测法。文献［10］基于系统负荷分配进行预测，采用分配系数实现对每条母线负荷预测，该方法不考虑负荷区域不一致问题，导致预测准确率较低。文献［11］采用状态估计对历史数据进行全网负荷模型建设，并动态调整分配系数，但缺乏实例验证。文献［12］采用PSO 算法对BP 神经网络算法进行优化，使之不易陷入局部极小，增强其泛化能力。文献［13～15］采用模糊系统和人工神经网络混合法来实现母线负荷预测，并将负荷基于气象影响情况分为无关负荷和有关负荷，训练时间较长。文献［16～18］分别采用分形外推法对短期负荷进行预测、基于概率密度的支持向量机回归法等多种单一的负荷预测算法，其精度较低。鉴于以上模型训练的复杂性及预测精度偏低等问题，本文采用最小二乘法及加权马尔科夫链模型相结合的方法，探索基于历史母线负荷数据的变化规律，并针对具体的母线负荷数据进行数据模型拟合分析检验。

2 最小二乘法

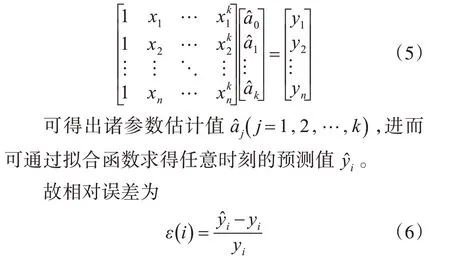
最小二乘法是以误差的平方和最小为准则根据观测数据估计线性模型中未知参数的一种参数估计方法。设X 和Y 两个物理量之间的函数关系为

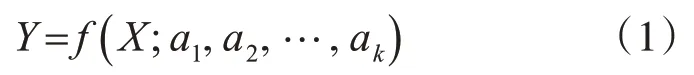
若a1,a2,…,ak等参数未知，f 已知，对于观测序列{xi,yi}，i=1,2,…,n，利用该序列对参数a1,a2,…,ak进行估计。

设拟合多项式为

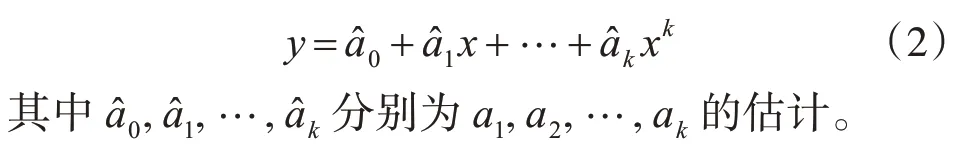
各点到这条曲线的距离之和，即偏差平方和如下：

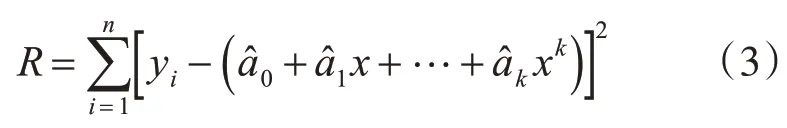
则最小二乘法的要求就是R 最小，采用求极值的方式对参数a1,a2,…,ak进行求解。

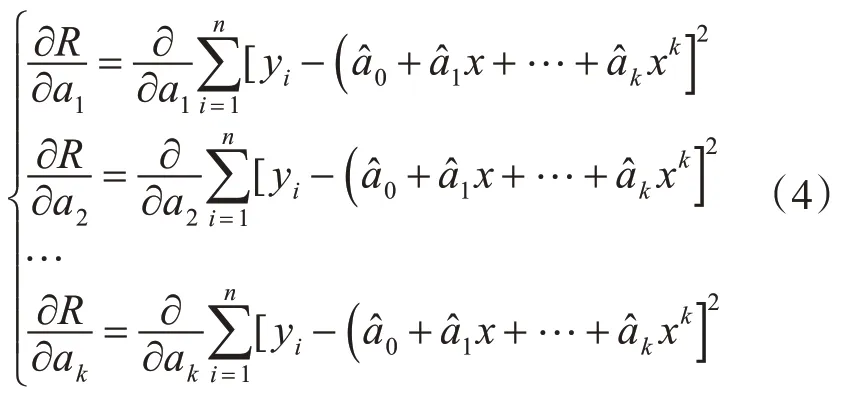
进一步的求解：

3 马尔科夫链模型

3.1 马尔科夫链

对于随机序列{xn},n≥0，满足对于任意的i0,i1,i2,…in,in+1∈S，其中S为状态空间，若有

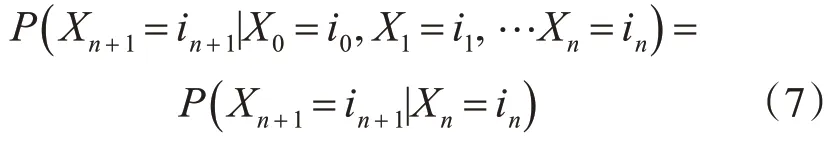
则称其为马尔科夫链，其某一时刻状态转移的概率仅依赖于前一个时刻的状态。

3.2 状态转移矩阵

4 最小二乘法-加权马尔科夫链模型

最小二乘法以误差的平方和最小为准则进行母线负荷预测，对于高精度曲线拟合，仅考虑误差平方和其效果不够理想。而马尔科夫链模型具有“无后效性”，能够反映母线负荷的随机过程特征，对于波动性较大的情况效果较好。故而，结合最小二乘法并辅以加权马尔可夫模型，其预测精度较高。同时，为了减少状态转移矩阵的生成频率实现对中长期母线负荷预测，采用固定频次的状态转移矩阵生成，并基于部分指数加权法实现对预测结果的优化。

4.1 相对误差状态划分

将基于最小二乘法拟合的母线负荷数值与实际数值的相对误差ε(k)划分为m 个状态，若ε(k)∈(d1i,d2i),i=1,2…,m，那么第k 个时间点的相对误差处于Ei状态，其中d1i、d2i为状态Ei的上界和下界。

4.2 各阶自相关系数和权重

基于自相关系数对马尔科夫链进行加权改进，即通过对原始数据进行自相关分析来求取自相关系数。对于自相关系数绝对值较大的，赋予较大权重。

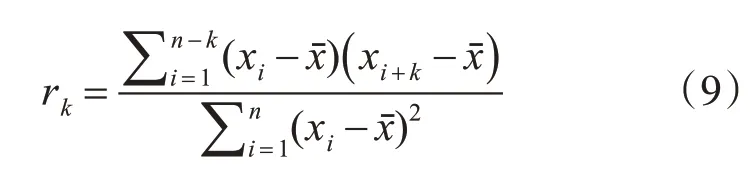
其中rk为第k 阶的自相关系数；xi为i 时刻的样本数据；xˉ为样本数据的均值。

将自相关系数归一化，得到各阶权重为

其中m为按预测需要计算到的最大阶数。

4.3 加权马尔科夫链预测

选择离预测时间最近的k 个时间点，将这k 个时间点的相对误差所在的状态作为初始状态，结合其相应的转移概率矩阵即可预测出该时刻的状态概率i∈E；将同一状态的各预测概率加权和作为最终转移概率：

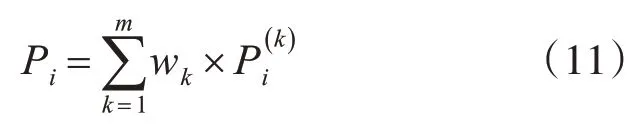
max{Pi} 所对应的i 即为预测时刻相对误差所在的状态。

进而得到优化后的预测值为

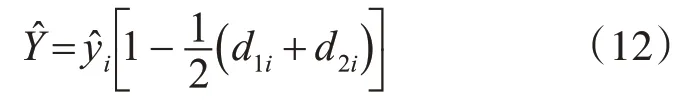
4.4 部分指数加权法

设置状态转移矩阵的生成频率为p，对于随机序列{ }xn,n≥0，描述为{x0,x1,…xp,xp+1,…x2p,…xn},n≥0，若t=kp,k≥0 则采用式（12）预测其结果；否则，t 时刻的母线负荷预测值视为t-1 时刻加权预测值与t时刻的非加权预测值的加权平均，即：

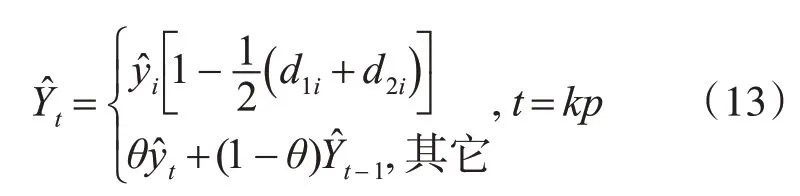
5 预测过程

本文采用最小二乘法-加权马尔科夫链模型实现母线负荷预测，首先确定预测时间段，然后基于其日期值选择前k 个周期内的母线负荷数据及距离预测日期较近的s 个测点数值构建历史数据序列，然后采用最小二乘法对其进行拟合，对其拟合的相对误差基于误差结果数值划分为多个状态，进而构建马尔科夫链模型的状态转移矩阵，通过概率加权法对其预测结果进行优化，同时根据状态转移矩阵生成频次设定采用部分指数加权法实现对非设定周期时间的母线负荷预测。

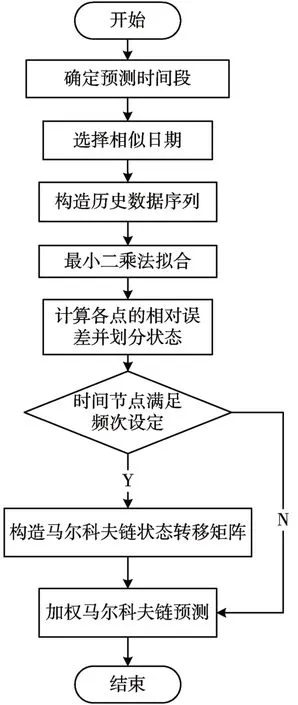
图1 母线负荷预测流程

6 算例分析

为了减少母线负荷数据的不稳定性，本文以新疆某变电站的一条110kV 母线近一年某特定日期的负荷数据及本月该日前3 天的数据为基础，采用最小二乘法-加权马尔科夫模型对该母线预测负荷数据。首先，本文通过分析母线负荷变化率与平均负荷变化率，识别异常点，并采用插值法对母线原始负荷数据进行预处理。其预处理后数据曲线如图2所示。

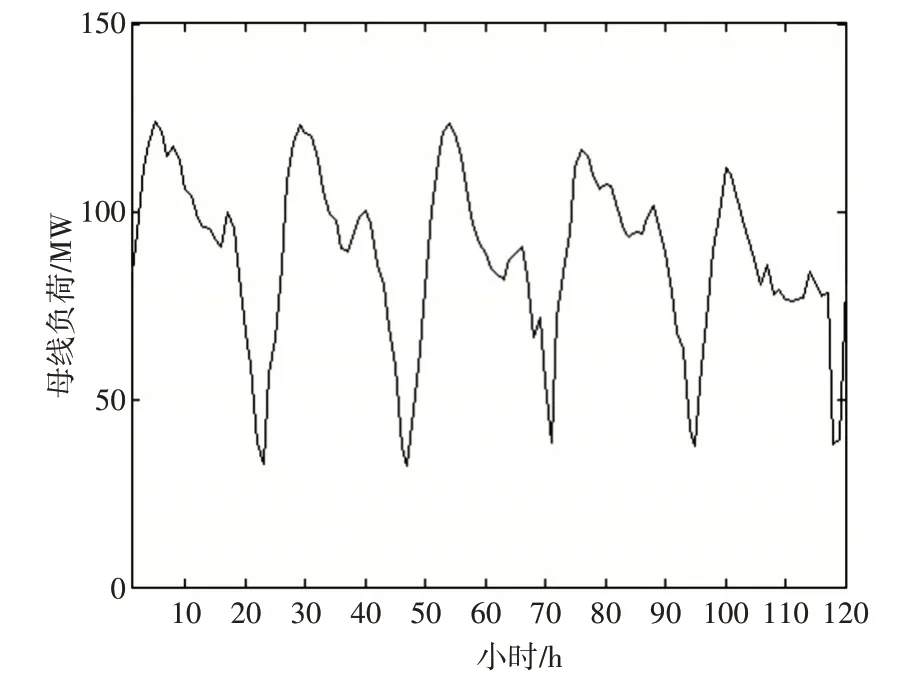
图2 母线负荷曲线测试数据

6.1 最小二乘法预测

对经过预处理之后的数据采用最小二乘法进行曲线拟合：采用60%的训练数据集，20%的测试数据集和20%的验证数据集的原则对模型进行训练。以最近的24个采集点为例，其拟合结果如下。

根据相对误差实际情况及马尔科夫链状态划分方法，将相对误差划分为5 种状态，划分标准如表2。其对相对误差的划分结果见表1的状态列。

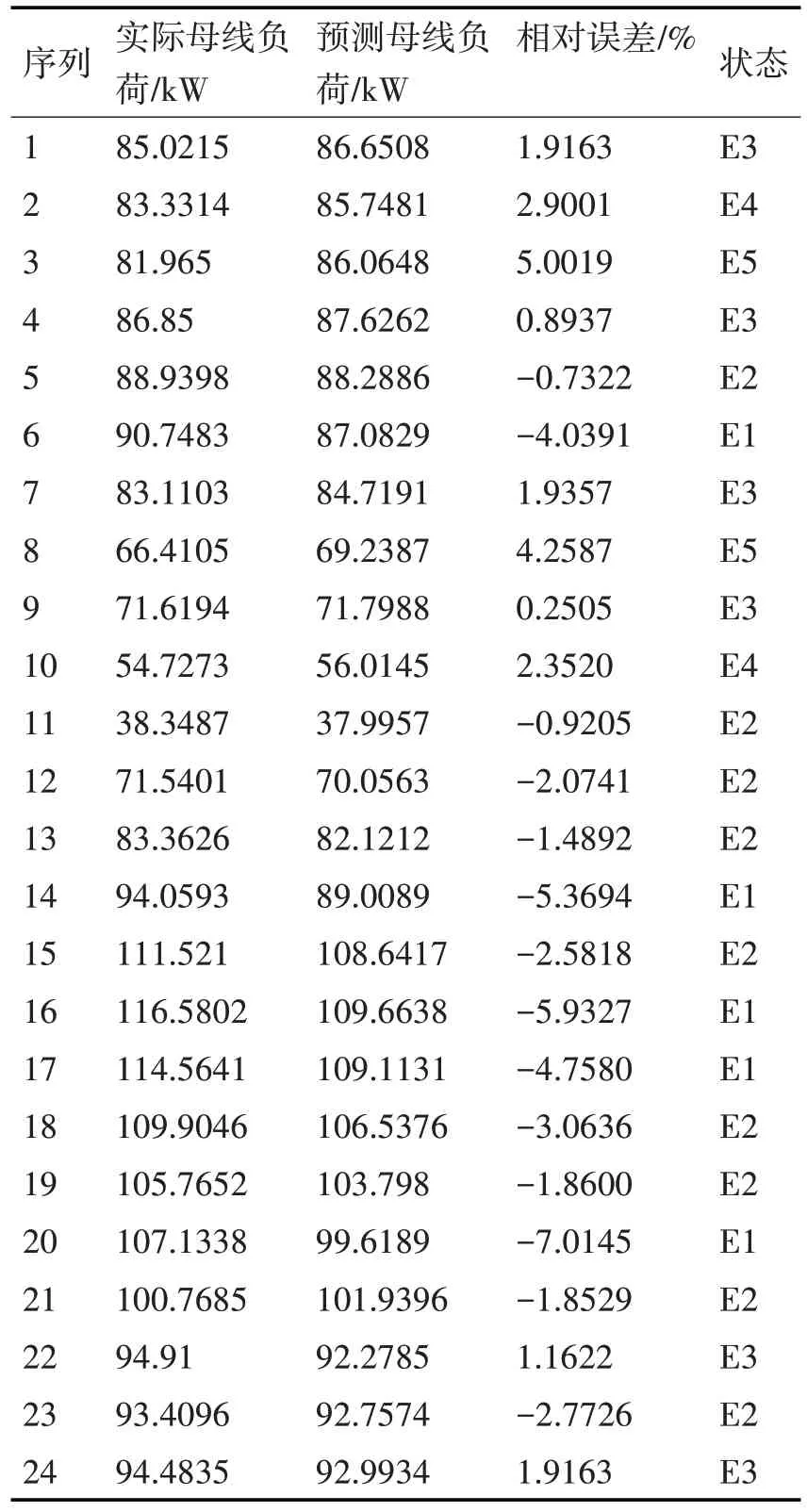
表1 母线负荷最小二乘法拟合结果

表2 状态划分

6.2 加权马尔科夫链预测

根据表1 状态列数值计算出1 到5 步长的状态转移矩阵。

根据式（9）和式（10）计算各阶自相关系数和权重，如表3所示。

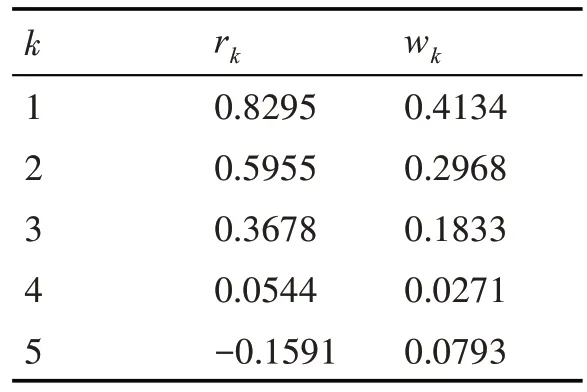
表3 各阶自相关系数和权重

由概率转移矩阵和1到5阶的权重对之后的母线负荷进行预测。由表4可知，序列20的状态处于E1，其最终预测结果为105.5960kW，其相对误差为-1.4353%。

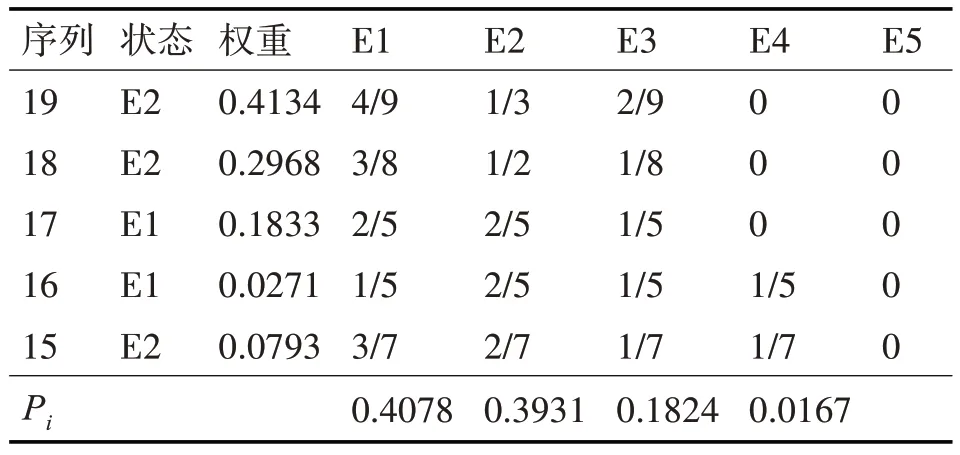
表4 相对误差状态预测表

通过逐步更新状态转移矩阵，并采用加权马尔科夫链模型对最小二乘法训练结果进行修正，其预测结果曲线展示如图3。

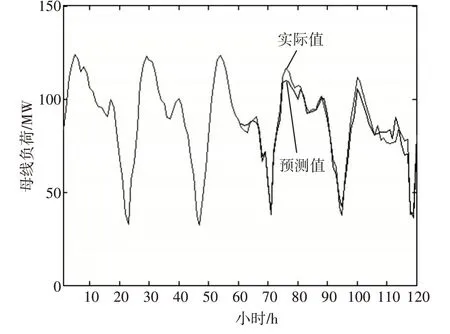
图3 母线负荷曲线预测结果

对其后10 个数据点采用部分指数加权法拟合结果详细信息如表5所示。

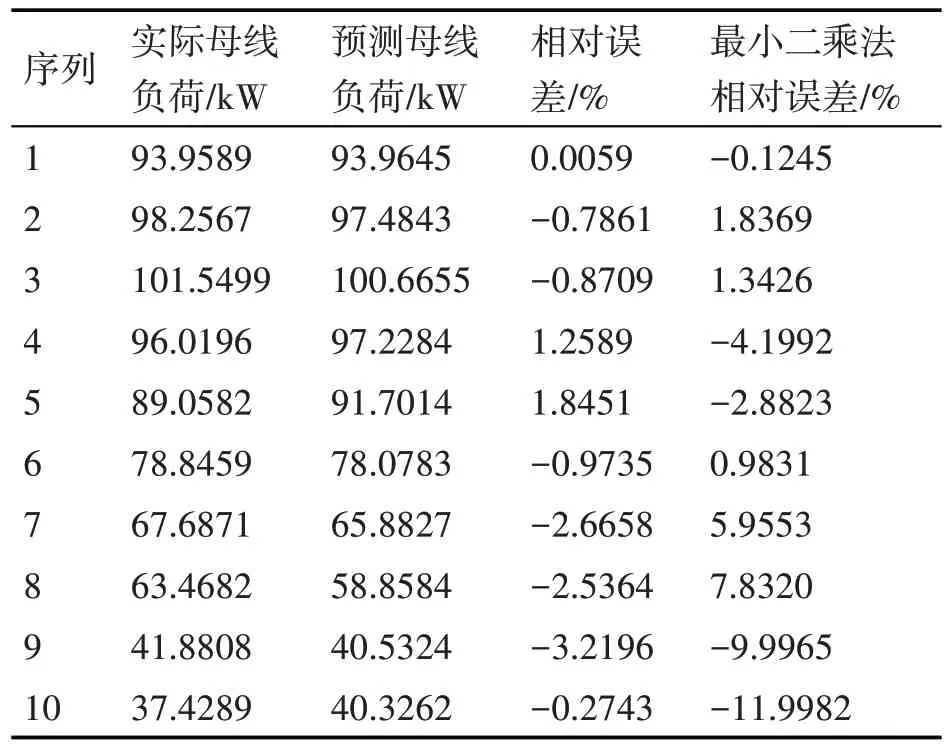
表5 母线负荷最小二乘法-加权马尔科夫链模型拟合结果

由表5 可得，最小二乘法-加权马尔科夫链模型的算法较最小二乘法预测精度有较大提升，其相对误差平均降低了3.27%。

7 结语

本文基于母线负荷的时序性及不稳定性，采用最小二乘法实现母线负荷曲线的拟合，并基于其拟合误差采用加权马尔科夫链模型进行状态划分及最大转移概率预测，对初始拟合数值进行了调优，同时，为了减少状态转移矩阵的生成频次采用了部分指数加权法进行优化，从而使得预测误差更小，准确度更高，进而使得母线负荷预测结果更好地为电网安全校核、运行方式变更等辅助决策提供参考依据。